高考数学压轴题的解题思路方法与解题策略

■郑州一中 孙锡九

高考数学全国卷第2 1题是多年延续下来且定型的有关导数的压轴试题,它在试卷中的地位和重要性是不言而喻的,试题主要涉及函数的单调性,函数的极值与值域,函数零点的个数,函数所含字母的取值范围,以及与导数有关的不等式证明等。由于试题承载了考查功能和选拔功能,所以第2 1题大多具有较大的难度,对考生的能力与素养有着较高要求。

近六年来,第2 1题所给出的函数表达式中均含有字母参数,给问题解决带来了更多的困难,令许多考生望而生畏。笔者认为,问题主要集中在如下一些方面：①不会或不能完整地对字母参数进行分类讨论;②对一些较为复杂和烦琐的导函数,方法单一或束手无策,不会转化和整合;③不会寻求极值点或不会确定零点存在的充要条件;④不会或不知道如何去构造函数;⑤不会或不知道利用放缩法、待定系数法、数形结合法、换元法、分析法、逆推法等数学方法去化归。

针对考生所存在的上面所列举的诸多困惑,本文把笔者对多年高考第2 1题研究的一些感悟呈现给读者,希望能对考生有所帮助。

因篇幅所限,上述问题无法一一涉及,又因为主要是第2 1题的解答思路、方法与策略,所以本文的解析并非标准解答模式,特予以说明。

例1 已知函数f(x)=l n(x+1)+a(x2-x),其中a∈R。

(Ⅰ)讨论函数f(x)的极值点的个数,并说明理由;

(Ⅱ)若对任意x＞0,f(x)≥0成立,求a的取值范围。

思路分析：f(x)的定义域为(-1,+∞),且表达式含字母参数a,故需分类讨论。

(1)若a=0,则f'(x)＞0,f(x)在(-1,+∞)上单调递增,即f(x)无极值点。

(2)若a≠0,设g(x)=2a x2+a x+1-a,则Δ=9a2-8a。

①当0＜a≤时,Δ≤0,g(x)＞0,即得f'(x)＞0,所以f(x)在(-1,+∞)上单调递增,即f(x)无极值点;

②当a＞时,Δ＞0,设g(x)=0的两

根为x,x(x＜x),x=(-a-12121,所以g(x)在(-1,+∞)上有两个零点,即f(x)有两个极值点;

③当a＜0时,由0,知x1,x2为一正根和一负根,又g(-1)＞0,所以x1＜-1＜x2,f(x)在(-1,x2)上单调递增,在(x2,+∞)上单调递减,故f(x)只有一个极值点。

(Ⅱ)由(Ⅰ)知,当时,f(x)在(0,+∞)上单调递增,又由f(0)=0,可知f(x)＞0恒成立。

(1)当时,由于,此时无法判断1-a的正负,所以还要分进行讨论。

①若＜a≤1,g(x)无正根,f(x)在(0,+∞)上单调递增,f(x)＞f(0)=0;

②若a＞1,x1x2＜0,即x1＜0,x2＞0,则f(x)在(0,x2)上单调递减,而f(0)=0,故f(x)＞0不恒成立。

(2)当a＜0时,f(x)=l n(x+1)+a x2-a x,由l n(x+1)＜x(x＞0),得f(x)＜,当x＞1-时,f(x)＜0,即f(x)≥0不成立。

综上,得0≤a≤1。

评析：(1)因为a∈R,故要对所有实数a的取值范围加以讨论,不能遗漏;(2)因为第1问与第2问里x的取值范围不同,所以讨论要注意极值点是否在定义域之内;(3)放缩法是证明不等式问题经常采用的方法。

例2 (2 0 1 8年“南柳联考”)已知函数f(x)=l nx-a x2+(2-a)x。

(1)讨论f(x)的单调性。

(2)设f(x)的两个零点分别是x1,x2,求证：

思路分析：(1)由已知条件得f'(x)=

①当a≤0时,f'(x)＞0,f(x)在(0,+∞)上单调递增。

②当a＞0时,由f'(x)=0得x=,当0＜x＜时 ,f'(x)＞0,f(x)在 (0 ,)上单调递增;当x≥时,f'(x)≤0,f(x)在上单调递减。

(2)当x1,x2是f(x)的两个零点时,如何证明如何构造一个新函数?构造一个什么样的新函数才能有利于问题的解决?

由(1)知道,当a＞0时是f(x)的一个极大值点,f(x)的两个零点分别位于的两侧,我们不妨设因为f'(x)在上单调递减,所以证明等价于证明下面就从分析的必要条件入手。

证明F(x)＜0,注意到F()=0,所以只需证F(x)＜F(),则只要证F(x)在(0)上单调递增即可。

事实上,F'(x)=f'(x)-[f (-x)']

显然F'(x)＞0,问题得到解决。

评析：(1)解答第2问时,一定要结合第1问的情况,注意利用第1问的结果。(2)要学会自觉运用分析的方法,这样的解题才具有方向性,避免走弯路。

例3 已知函数f(x)=ae2x+(a-2)·ex-x。

(1)讨论f(x)的单调性;

(2)若f(x)有两个零点,求a的取值范围。

思路分析：本题两问均与字母参数a有关,所以要对a分类讨论。

(1)f'(x)=2ae2x+(a-2)ex-1=(aex-1)(2 ex+1)。

当a≤0时,f'(x)＜0,f(x)在(-∞,+∞)上单调递减。

当a＞0时,令aex=1,得x=l n, 当

x＞l n时,f'(x)＞0,f(x)在(l n,+∞)上单调递增;当x＜l n时, f'(x)＜0,f(x)在 (- ∞,l n)上单调递减。

(2)由(1)知,当a≤0时,f'(x)至多一个零点。f(x)有两个零点的必要条件是a＞0,由(1)知,此时x=l n是f(x)的极小值点,所以f(x)有两个零点的充要条件是f(l n)＜0,且在l n的左、右两侧均存在函数值大于零的点。

由f(l n)=1-+l na＜0,得l na+1＜,当0＜a＜1时,此不等式成立。

当a≥1时,不等式不成立,故0＜a＜1。当0＜a＜1时,l n＞0,在l n的左侧 取点x=-1,则

现在问题是：如何在l n的右方取点?由于l n的值不定,那么取什么样的点才能使该点在l n的右方,且在该点处的函数值还必须是正数?

这里我们采取待定系数法,设满足上述条件的点为x=t,f(t)=ae2t+(a-2)ett=et(aet+a-2)-t＞0,易知et＞t,所以只需aet+a-2=1即可,所以et=-1,解得

t=l n(- 1)。

因l n(-1)=l n(+-1)＞l n, 故取t=l n(a3- 1),有f(l n (a3- 1))＞0。

综上,当0＜a＜1时,f(x)有两个零点。

评析：(1)上面用到的et＞t要加以证明;(2)待定系数法是一种逆向思维与分析的方法,它对拓宽思路很有益处。

例4 设函数f(x)=l n(x+1)+,曲线y=f(x)与直线y=x在(0,0)处相切。

(1)求a,b值;

(2)证明：当

思路分析：(1)由已知条件可得f'(x)=得a=0,b=-1。

(2)证不等式即证在(0,2)上成立,此不等式中既有自然对数,又有根式和分式,如果直接构造函数求导,不仅运算烦琐,而且所求导函数形式复杂,不易求解,故应考虑放缩法。

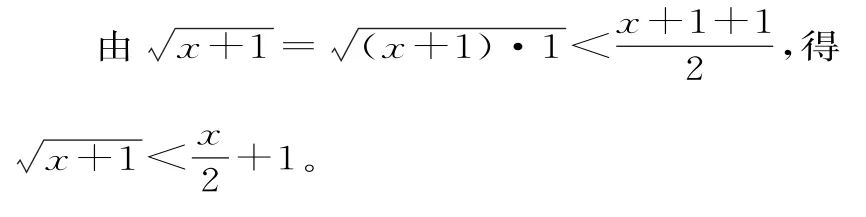
令h(x)=l n(x+1)-x,则h'(x)=当x≥0时,h'(x)≤0,即h(x)在[0,+∞)上单调递减,所以h(x)≤h(0)=0,得l n(x+1)≤x,当x=0时取等号。

因为0＜x＜2,所以g'(x)＜0。

所以g(x)在(0,2)上单调递减,当x→0时,g(x)→0,所以g(x)＜0。

综上可得

评析：(1)放缩法是用在g'(x)的表达式上,而不要直接对g(x)放缩,那样就不是证明原不等关系了。

(2)导数问题中比较常用的不等式有：ex≥x+1,两边取对数有x≥l n(x+1)(x＞-1),用x-1代换x,得ex-1≥x,x-1≥l nx(x＞0),用x+1代换x,得ex+1≥x+2,x+1≥l n(x+2)(x＞-2),以及其他变形不等式,如等,还有本题中用到的由均值不等式推出的其他不等关系。

(3)以上不等式在使用时要先给出证明。

例5 已知函数f(x)=a x2-a-l nx(a∈R)。

(1)讨论f(x)的单调性;

思路分析：本题两问均与字母参数有关,所以需进行分类讨论。

(1)显然当a≤0时,f'(x)＜0,所以f(x)在(0,+∞)上单调递减。

当a＞0时,令2a x2=1,得x=当时,f'(x)＞0,则 f(x)在上单调递增;当时,f'(x)＜0,则f(x)在上单调递减。

(2)根据题目要求,我们可以将字母参数a从不等式中反解出来,这样得到然后求右边函数的最大值,但是可以想象,对右式求导后的式子必定非常烦琐,于是我们可以另辟蹊径。注意到第1问已经对f(x)的单调性做过讨论,所以我们可以从不等式右边的入手。

设令h(x)=ex-1-x,由h'(x)=ex-1-1＞0知h(x)在(1,+∞)上单调递增,所以h(x)＞h(1)=0,得g(x)在(1,+∞)上单调递增,所以g(x)＞g(1)=0。

又由(1)知,当a≤0时,f(x)单调递减,所以f(x)＜f(1)=0,得f(x)＜g(x),即所证不等式在a≤0时不成立。

当a＞0时,由于x∈(1,+∞),所以还要讨论与1的大小。

当,由(1)知,f(x)在上 单调递减,所 以 当1＜时,f(x)＜f(1)=0,不等式

0f(x)＞g(x)不成立。

当＜1,在(1,+∞)上f(x)＞0,g(x)＞0,无法判断f(x)-g(x)的符号,故构造函数φ(x)=f(x)-g(x)(x＞1),由f(1)=g(1)=0,得φ(1)=0,则f(x)-g(x)＞0等价于φ(x)＞φ(1)(x＞1),故只需证明φ(x)在(1,+∞)上单调递增即可。

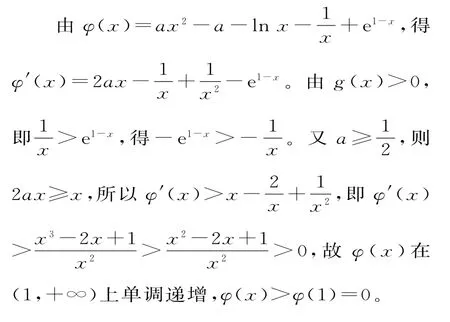
综上,当a≥时,f(x)＞g(x)在(1,+∞)恒成立。

评析：这里采用了化繁为简,各个击破的解题策略和放缩法。

例6 已知f(x)=a(x-l nx)+

(1)讨论f(x)的单调性;

(2)当a=1时,证明：f(x)＞f'(x)+对任意x∈[1,2]成立。

思路分析：(1)f(x)的定义域是x＞0,其表达式含字母参数a,所以要对a进行分类讨论。

由条件得这里要分a=0与a≠0两种情况。

当a≠0时,f'(x)=则要分a＞0与a＜0两种情况,在a＞0时,还要分三种情况,一定要对全体实数a讨论,做到不重不漏。

①当a≤0时,仅有x=1为极值点,当0＜x＜1时,f'(x)＞0,f(x)在(0,1]上单调递增;在(1,+∞)上单调递减。

②当,当0＜x≤1时,f'(x)≥0,f(x)在(0,1]上单调递增;当时,f'(x)≤0,f(x)在上单调递减;当＞0,f(x)在上单调递增。

③当a=2时,＞0,f(x)在(0,+∞)上单调递增。

④当a＞2时,当0＜x≤f(x)在上 单 调递增;当在上单调递减;当x＞1时,f(x)＞0,f'(x)在(1,+∞)上单调递增。

然后综上所述,给出单调性的结论即可。

(2)当a=1时,f(x)-f'(x)=x-l nx要证f(x)-f'(x)＞在x∈[1,2]上成立,常规思路是证明f(x)-f'(x)的最小值大于,不难看出f(x)-f'(x)的表达式比较烦琐冗长,它的导函数是一个四次分式函数,更是令人望而生畏。

这里我们注意到,由l nx≤x-1(x＞0),可得x-l nx-1≥0,当x=1时取等号,故只要证即可。

设h(x)=x∈[1,2],则

令g(x)=-3x2-2x+6,显然g(x)在[1,2]上单调递减,由g(2)=-1 0,g(1)=1,知在[1,2]中有x0,使得g(x0)=0,当1≤x＜x0时,g(x)＞g(x0)=0;当x0≤x≤2时,g(x)≤g(x0)=0,所以x0是h(x)的一个极大值点,h(x)的最小值应为h(1)与h(2)中的较小者,由h(1)=2,h(2)=,得

h(x)≥。

因为x-l nx-1≥0与h(x)≥不能同时取等号,故有f(x)-f'(x)＞,命题得证。

评析：(1)这里的x-l nx-1≥0(x＞0)需加以证明。(2)面对一个较为繁杂的表达式,我们可以采用一分为二,各个击破的策略。(3)注意放缩法和常见不等式的应用。