高三专题复习———分类讨论思想

■江苏省太仓高级中学 陆 丽

分类讨论思想作为高中数学最基本的思想方法之一,历来是高考数学考查的一个重要内容。纵览近五年新课标高考试题,分类讨论思想在高考试题中频频出现,已成为高考数学的一个热点,也是高考的难点。高考试卷中经常会有几道题,其解题思路是直接依赖于分类讨论思想的,特别在解答题中(尤其是导数与函数)常有一道分类讨论求解的把关题,选择题、填空题也会出现不同情形的分类讨论题。

一、知识要点概述

1.分类讨论思想方法的原理及作用。

在研究与解决数学问题时,如果问题不能以同一种方法处理或同一种形式表述、概括,可根据数学对象的本质属性的相同点和不同点,按照一定的原则或某一确定的标准,在比较的基础上,将数学对象划分为若干既有联系又有区别的部分,然后逐类进行讨论,再把这几类的结论汇总,从而得出问题的答案,这种研究解决问题的思想方法就是分类讨论的思想方法。分类讨论的思想方法是中学数学的基本方法之一,在近几年的高考试题中都把分类讨论思想方法列为重要的思想方法来考查,体现出其重要的位置。分类讨论的思想方法不仅具有明显的逻辑性、题型覆盖知识点较多、综合性强等特点,而且还有利于对考生知识面的考查,需要考生有一定的分析能力、分类技巧,对考生能力的考查有着重要的作用。分类讨论思想方法的实质就是化解数学问题中各种条件的制约及变动因素的影响而采取的化整为零、各个突破的解题手段。

2.引起分类讨论的主要原因。

(1)问题所涉及的数学概念是分类进行定义的。例如,|a|的定义分a＞0,a=0,a＜0三种情况。这种分类讨论题型可以称为概念型。

(2)问题中涉及的数学定理、公式和运算性质、法则有范围或者条件限制,或者是分类给出的。例如,等比数列的前n项和的公式,分q=1和q≠1两种情况。这种分类讨论题型可以称为性质型。

(3)解含有参数的题目时,必须根据参数的不同取值范围进行讨论。例如,解不等式a x＞3时分a＞0,a=0,a＜0三种情况讨论。这种称为含参型。

另外,某些不确定的数量、不确定的图形的形状或位置、不确定的结论等,都可以通过分类讨论,保证其完整性,使之具有确定性。

二、解题方法指导

1.运用分类讨论思想方法的步骤。

(1)确定标准;

(2)合理分类;

(3)逐类讨论;

(4)归纳总结。

2.简化分类讨论的策略。

(1)消去参数;

(2)整体换元;

(3)变更主元;

(4)考虑反面;

(5)整体变形;

(6)数形结合;

(7)缩小范围。

3.进行分类讨论时需遵循的原则。

分类的对象是确定的,标准是统一的,不遗漏、不重复,科学地划分,分清主次,不越级讨论。其中最重要的一条是“不漏不重”。

4.解题时把好“四关”。

(1)要深刻理解基本知识与基本原理,把好“基础关”;

(2)要找准划分标准,把好“分类关”;

(3)要保证条理分明,层次清晰,把好“逻辑关”;

(4)要注意对照题中的限制条件或隐含信息,合理取舍,把好“检验关”。

三、基本题型分析

1.由概念、法则、公式、性质引起的分类讨论。

例1 (1)函数f(x)=若f(1)+f(a)=2,则a的所有可能值的集合为____。

(2)等比数列{an}的各项均为实数,前n项和为Sn,已知则a=

8____。

解析：(1)f(1)=e0=1,即f(1)=1。

当a≥0时,f(a)=1=ea-1,所以a=1;

当-1＜a＜0时,f(a)=s i n(πa2)=1,所以所以a2=2k+只能取0,此时因为-1＜a＜0,所以

所以a的所有可能值的集合为

(2)设等比数列{an}的公比为q。

若q=1时,有S6=2S3,但由已知S6=

当q≠1时,解得则

友情提示：解决由概念、法则、公式、性质引起的分类讨论问题一般分四个步骤：

第一步：确定需分类的目标与对象。确定需要分类的目标,一般把需要用到公式、定理解决问题的对象作为分类目标。

第二步：根据公式、定理确定分类标准。运用公式、定理对分类对象进行区分。

第三步：分类解决“分目标”问题。对分类出来的“分目标”分别进行处理。

第四步：汇总“分目标”。将“分目标”问题进行汇总,并作进一步处理。

【变式训练一】

(1)设等比数列{an}的公比为q,前n项和Sn＞0(n=1,2,3,…),则q的取值范围是____。

(2)若函数f(x)=l o g(a2-3)(a x+4)在[-1,1]上是单调增函数,则实数a的取值范围是____。

2.由图形位置或形状引起的分类讨论。

例2 (1)设A,B是椭圆长轴的两个端点。若C上存在点M满足∠AMB=1 2 0°,则m的取值范围是( )。

(2)将一张长8c m,宽6c m的长方形纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1c m2,S2c m2,其中S1≤S2。记折痕长为lc m。

①若l=4,求S1的最大值;

②若S1∶S2=1∶2,求l的取值范围。

解析：(1)当0＜m＜3时,焦点在x轴上,要使C上存在点M满足∠AMB=1 2 0°,则1;当m＞3时,焦点在y轴上,要使C上存在点M满足∠AMB=1 2 0°,则故m的取值范围为(0,1]∪[9,+∞),故选A。

(2)不妨设纸片为长方形A B C D,A B=8c m,A D=6c m,其中A点在面积为S1的部分内。折痕有下列三种情形：如图1,折痕的端点M,N分别在边A B,A D上;如图2,折痕的端点M,N分别在边A B,C D上;如图3,折痕的端点M,N分别在边A D,B C上。

图1

①在图1和图2中,MN≥6,故当l=4时,折痕必定是图1中情形。

设AM=xc m,AN=yc m,则x2+y2=1 6。因为x2+y2≥2x y,当且仅当x=y时取等号,所以S1=x y≤4,当且仅当x=时取等号,即S1的最大值为4。

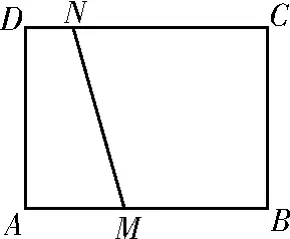
图2

图3

②由题意知,长方形的面积为S=6×8=4 8。

因为S1∶S2=1∶2,S1≤S2,所以S1=1 6,S2=3 2。

当折痕是图1中的情形时,设AM=xc m,AN=yc m,则

故f'(x)与f(x)的变化情况如表1：

___________________表1

所以f(x)的取值范围为[6 4,8 0],从而l的范围是

当折痕是图2中的情形时,设AM=xc m,DN=yc m,则(x+y)×6=1 6,即

友情提示：几类常见的由图形的位置或形状变化引起的分类讨论：(1)二次函数对称轴的变化;(2)函数问题中区间的变化;(3)函数图像形状的变化;(4)直线由斜率引起的位置变化;(5)圆锥曲线由焦点引起的位置变化或由离心率引起的形状变化;(6)立体几何中点、线、面的位置变化等。

【变式训练二】

(1)已知双曲线的离心率为则其渐近线方程为____;

图4

3.由问题中的条件是分类给出的而引起的分类讨论。

例3 设a1,a2,…,an是各项均不为零的n(n≥4)项等差数列,且公差d≠0,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列。

(1)当n=4时,求的数值;

(2)求n的所有可能值。

解析：(1)当n=4时,a1,a2,a3,a4中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。

若删去a2,则=a1·a4,即(a1+2d)2=a1·(a1+3d),化简得a1+4d=0,得=-4。

若删去a3,则=a1·a4,即(a1+d)2=a1·(a1+3d),化简得a1-d=0,得=1。

综上可得=-4或=1。

(2)当n=5时,a1,a2,a3,a4,a5中同样不可能删去a1,a2,a4,a5,否则会出现连续三项。

若删去a3,则a1·a5=a2·a4,即a1(a1+4d)=(a1+d)(a1+3d),化简得3d2=0,因为d≠0,所以a3不能删去。

当a≥6时,不存在这样的等差数列。事实上,在数列a1,a2,a3,…,an-2,an-1,an中,由于不能删去首项或末项,若删去a2,则必有a1·an=a3·an-2,这与d≠0矛盾;同样若删去an-1也有a1·an=a3·an-2,这与d≠0矛盾;若删去a3,…,an-2中任意一个,则必有a1·an=a2·an-1,这与d≠0矛盾。(或者说：当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)

综上所述,n=4。

友情提示：由于问题中的条件包含多种情形,每一种情形都会产生一个结果,故在解题时必须分类讨论,而且不可漏掉任何一种情形,解答这类问题必须要做到耐心细致,否则答案会出现“对而不全”的现象,而对于填空题来说更是“前功尽弃”。

【变式训练三】

(1)在 △A B C 中,已 知,且△A B C的一个内角为直角,则实数k的值为____。

(2)在等差数列{an}中,a3+a4=4,a5+a7=6。

①求{an}的通项公式;

②设bn=[an],求数列{bn}的前1 0项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2。

4.由变量或参数引起的分类讨论。

例4 设a＞0,函数f(x)=x2+a|l nx-1|。

(1)当a=1时,求曲线y=f(x)在x=1处的切线方程;

(2)当x∈[1,+∞)时,求函数f(x)的最小值。

解析：(1)当a=1时,f(x)=x2+|l nx-1|,令x=1得f(1)=2,f'(1)=1,所以切点为(1,2),切线的斜率为1,所以曲线y=f(x)在x=1处的切线方程为xy+1=0。

(2)①当x≥e时,f(x)＞0=x2+

因为a＞0,所以f'(x)＞0恒成立,所以f(x)在[e,+∞)上是增函数。

故当x=e时,ymin=f(e)=e2。

②当1≤x≤e时,f(x)=x2-al nx+

当时,f'(x)在x∈(1,e)上为正数,所以f(x)在区间[1,e)上为增函数。故当x=1时,ymin=1+a,此时f(1)＜f(e)。

当即2＜a＜2 e2时,f'(x)在上 为 负 数,在x∈上为正数。

当时,f'(x)在x∈(1,e)上为负数,所以f(x)在区间[1,e]上为减函数,故当x=e时,ymin=f(e)=e2。

综上所述,当a≥2 e2时,f(x)在x≥e和1≤x≤e时的最小值都是e2,所以此时f(x)的最小值为f(e)=e2;当2＜a＜2 e2时,f(x)在x≥e时的最小值为所以此时f(x)的最小值为当0＜a≤2时,f(x)在x≥e时的最小值为e2,在1≤x＜e时的最小值为f(1)=1+a,而f(1)＜f(e),所以此时f(x)的最小值为f(1)=1+a。

所以函数y=f(x)的最小值为ymin=

友情提示：一般地,遇到题目中含有参数的问题,常常结合参数的意义及对结果的影响进行分类讨论。这类问题有两种情形：(1)由于所求的变量或参数的取值不同会导致结果不同,所以要对某些问题中所求的变量进行讨论;(2)有的问题中虽然不需要对变量讨论,但却要对参数讨论。在求解时要注意讨论的对象,同时应理顺讨论的目的。

【变式训练四】

(1)若不等式x2+x-1＜m2x2-m x对x∈R恒成立,则实数m的取值范围是____。

(2)当实数x,y满足时,a x+y≤4恒成立,则实数a的取值范围是____。

四、分类讨论高考备忘

分类讨论思想是将一个较复杂的数学问题分解(或分割)成若干个基础性问题,通过对基础性问题的解答来实现解决原问题的思想策略。对问题实行分类与整合,分类标准等于增加一个已知条件,实现了有效增设,将大问题(或综合性问题)分解为小问题(或基础性问题),优化解题思想,降低问题难度。

常见的分类讨论问题有：

(1)集合：注意集合中对空集∅的讨论。

(2)函数：对数函数或指数函数中的底数a,一般应分a＞1和0＜a＜1的讨论,函数y=a x2+b x+c有时候分a=0和a≠0的讨论,对称轴位置的讨论,判别式的讨论。

(3)数列：由Sn求an时分n=1和n＞1的讨论;等比数列中分公比q=1和q≠1的讨论。

(4)三角函数：角的象限及函数值范围的讨论。

(5)不等式：解不等式时含参数的讨论,基本不等式相等条件是否满足的讨论。

(6)立体几何：点线面及图形位置关系的不确定性引起的讨论。

(7)平面解析几何：直线点斜式中k分存在和不存在的讨论,直线截距式中分b=0和b≠0的讨论;轨迹方程中含参数时对曲线类型及形状的讨论。

(8)去绝对值时的讨论及分段函数的讨论等。

【变式训练一答案】

(1)因为{an}是等比数列,Sn＞0,可得a1=S1＞0,q≠0。

当q=1时,Sn=n a1＞0;当q≠1时,

则有解得-1＜q＜1,或q＞1。

综上可得q的取值范围是(-1,0)∪(0,+∞)。

(2)复合函数的单调性可以依据同增异减来判断。由题意可得,当或时,函数在[-1,1]上是递增的,所以a的取值范围是(2,4)∪(-2,

【变式训练二答案】

(1)由于则a2=3b2。

若双曲线焦点在x轴上,渐近线方程为;若双曲线焦点在y轴上,渐近线方程为

综上可知,渐近线方程为或

(2)先考查拼成三棱柱,如图5所示,全面积为1 2a2+4 8。

再考查拼成四棱柱,如图6所示。

图5

①若A C=5a,A B=4a,B C=3a,则该四棱柱的全面积为S2=2×4a×3a+2(3a+4a)×= 2 4a2+2 8;

②若A C=4a,A B=3a,B C=5a,则该四棱柱的全面积为S2=2×4a×3a+2(3a+5a)×= 2 4a2+3 2;

③若A C=3a,A B=5a,B C=4a,则该四棱柱的全面积为S2=2×4a×3a+2(4a+5a)×= 2 4a2+3 6。

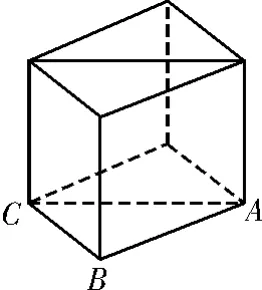
图6

在以上三种可能的情形中,全面积最小的是①,于是有2 4a2+2 8＜1 2a2+4 8⇒1 2a2＜2 0⇒0＜a＜,即a的取值范围是

【变式训练三答案】

(1)哪一个角为直角,不知道,故本题首先需要进行分类讨论,然后利用向量垂直的充要条件列出含有实数k的关系式,分别求之。

①若∠B A C=9 0°,即也就是,故2+3k=0,解得

②若∠B C A=9 0°,即也就是3),故-1+k(k-3)=0,解得

③若∠A B C=9 0°,即也就是故-2+3(k-3)=0,解得

综合上面的讨论可知或k=

(2)①设数列{an}的首项为a1,公差为d,由题意知解得,a1=1d=。

所以数列{bn}的前1 0项和为1×3+2×2+3×3+4×2=2 4。

【变式训练四答案】

(1)原不等式可化为(m2-1)x2-(m+1)x+1＞0对∈R恒成立。

①当m2-1=0且m+1=0时,不等式恒成立,所以m=-1。

② 当 m2-1≠0 时,则解得或m＜-1。

综合①②知,m的取值范围为(-∞,

(2)由约束条件作可行域,如图7所示。

图7

在x-y-1=0中,取x=1,得A(1,0)。由a x+y≤4得y≤-a x+4,要使a x+y≤4恒成立,则平面区域在直线y=-a x+4的下方。

若a=0,则不等式等价于y≤4,此时满足条件;

若-a＞0,即a＜0时,平面区域满足条件;

若-a＜0,即a＞0时,要使平面区域在直线y=-a x+4的下方,则只要B在直线上或直线下方,所以2a+1≤4,得

综上可得,实数a的取值范围是