Nested- LET柔性铰链设计与性能分析

邱丽芳 刘宁宁 陈明坤 岳 鑫

(北京科技大学机械工程学院， 北京 100083)

0 引言

柔顺机构主要依靠柔性单元的变形来实现全部运动和功能，同时实现运动、力和能量的传递和转换，为实现高速、精密、微型等对机构的高性能要求提供了新方法[1]。经过国内外学者多年的研究，柔顺机构在理论设计及运动分析方面有了一定的发展[2]，主要应用于微机电系统(MEMS)[3]、航空航天设备[4]、仿生机器人[5-6]及医疗仪器[7]等领域。

在柔顺机构中，为实现机构的正常运动并保证稳定性，需要依靠柔性铰链这一最小单元，可从根本上克服传统机构中存在的固有缺陷。近年来，柔性铰链的设计及应用得到了广泛研究。HOWELL等[8-10]在铰链结构上进行改善以提高性能以外，还利用组合[11]、去除材料[12]、静态平衡[13]等方法有效地减少了铰链的弯曲刚度，并且使约束方向刚度增大。LIU等[14]对单轴柔性铰链进行拓扑优化，利用多孔洞域结构提高其综合性能。PEI等[15]针对Cartwheel 型柔铰提出了两个伪刚体模型，并通过有限元分析对模型结果进行了验证。CHEN等[16-18]设计了多种切口形状的柔性铰链，并建立了适合各种拐点柔性铰链的理论模型[19]。邱丽芳等[20-23]从构型角度考虑，设计了Triple_LET、Deform_X型、双C型、平面外折展(OD- LEJ)柔性铰链等。

柔性铰链的设计是影响柔顺机构应用的关键，柔度和精度又是决定柔性铰链性能的主要因素。实际运动过程中，铰链转角增大的同时，抗拉压性能变差、转动轴线漂移、寄生运动等缺陷也成为了不可避免的问题，导致机构运动精度的下降。为提高精度，本文设计Nested- LET柔性铰链，推导其弯曲及拉压等效刚度理论计算公式，并定义修正系数，加工Nested- LET及LET实物模型，通过仿真分析及拉伸实验来验证铰链的性能，为高精度铰链的设计提供一种新思路。

1 Nested- LET铰链结构设计及理论分析

1.1 Nested- LET铰链结构设计

Nested- LET柔性铰链是基于外LET结构的柔性铰链，结合嵌套思想，在外LET铰链内部使用弯曲片段贯穿连接LET柔性片段，在其弯曲性能下降不明显的前提下，大幅度提高了柔性铰链的抗拉压性能。整体结构关于x轴、y轴对称，在产生弯曲变形的同时可改善外LET铰链由于中空结构造成的转动中心漂移，从而提高运动精度和抗拉压性能。Nested- LET柔性铰链的结构及受载情况如图1所示。

图1 Nested- LET柔性铰链结构及其受载情况Fig.1 Structure of Nested- LET joint and its loading condition

根据柔性片段的主要变形，分为2种扭转片段和4种弯曲片段，其余部分视为刚性连接。在如图1所示转矩作用下，铰链绕转轴发生弯曲变形。

1.2 Nested- LET铰链弯曲等效刚度

基于文献[8]提出的等效法，建立Nested- LET柔性铰链的弯曲等效弹簧模型，如图2所示。

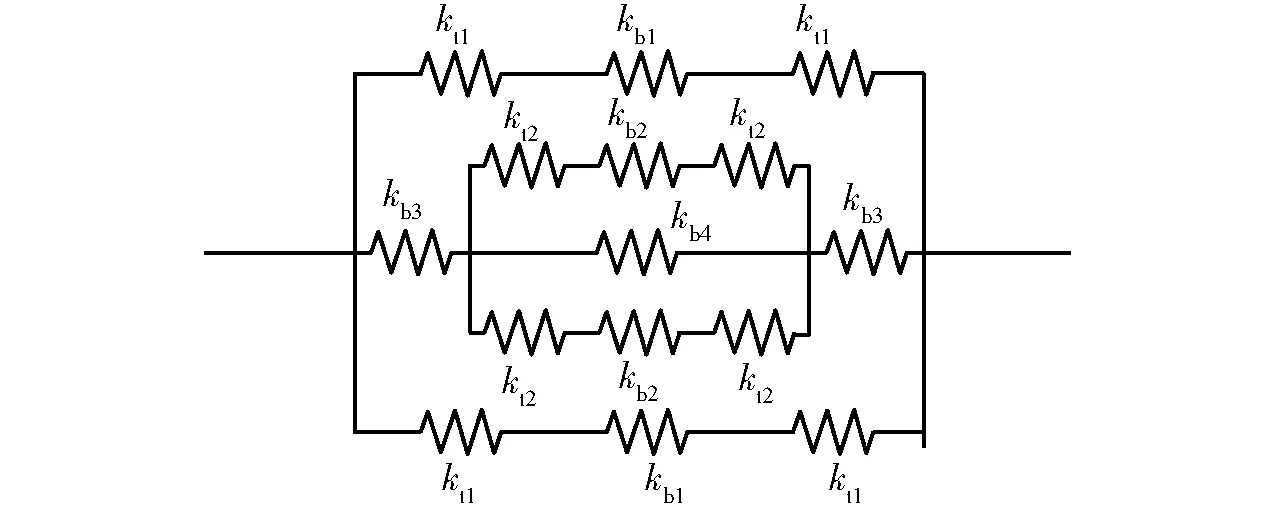
图2 Nested- LET柔性铰链弯曲等效弹簧关系示意图Fig.2 Corresponding spring model diagram of Nested- LET joint

根据弹簧的串并联关系可得出Nested- LET柔性铰链的弯曲等效刚度为

(1)

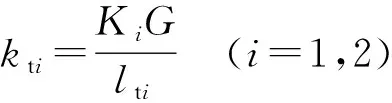
(2)

式中kti——柔性铰链扭转片段的等效刚度

lti——柔性铰链扭转片段长度

G——材料剪切模量

Ki为与扭转片段横截面几何特征相关的参数，CHEN等[24]提出的Ki近似方程不受截面宽厚比的影响，能保证较高的精度，表达式为

(3)

式中wti——柔性铰链扭转片段宽度

t——柔性铰链厚度

柔性铰链弯曲片段等效刚度用kbi表示，可将弯曲片段的变形视为受转矩下悬臂梁自由端产生的最大挠度，即

(4)

式中E——材料弹性模量

Ibi——弯曲片段惯性矩

lbi——弯曲片段长度

1.3 Nested- LET铰链拉压等效刚度

当Nested- LET柔性铰链在受到如图1所示的x轴方向拉力或压力F时，柔性片段分别发生拉压及弯曲变形，将拉压片段和弯曲片段分别等效为对应的拉压弹簧和弯曲弹簧。根据弹簧的串并联关系可得，Nested- LET柔性铰链的拉压等效刚度为

(5)

(6)

式中kbi,a——柔性铰链拉压片段的等效刚度

wbi——柔性铰链拉压力片段宽度

kti,a——柔性铰链弯曲片段的等效刚度

利用自由端受力的柔性悬臂梁的伪刚体模型进行计算。伪刚体模型中扭簧的刚度系数kfg可表示为

(7)

式中γ——特征半径系数，取0.85

Kθ——刚度系数，取2.65

I——弯曲梁惯性矩

L——弯曲梁长度

在垂直梁长度方向施加力F，伪刚体杆产生角度为Θ的变形，弯曲片段的挠度d可表示为

d=γLsinΘ

(8)

分析扭簧处的受力关系，可得

FγLcosΘ=kfgΘ

(9)

整理得

(10)

因为伪刚体模型角Θ极小，Θ≈sinΘ，则

(11)

利用三角函数关系可得到

(12)

综合式(7)～(12)，得

(13)

(14)

因此柔性铰链在拉压载荷作用下弯曲片段的等效刚度kti,a可表示为

(15)

式中Ii——弯曲片段截面惯性矩

Li——弯曲片段长度

2 实例计算与有限元分析

2.1 设计实例计算

Nested- LET柔性铰链的尺寸示意如图3所示。

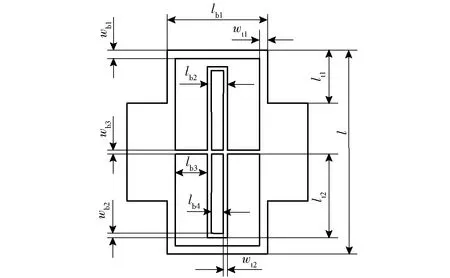
图3 Nested- LET柔性铰链尺寸示意图Fig.3 Dimension sketch of Nested- LET joint

本文中设计分析的铰链厚度t均为0.5 mm。所选材料为铍青铜，其弹性模量E=128 GPa，泊松比σ=0.29，屈服强度为[sy]=1 170 MPa。设计Nested- LET柔性铰链的尺寸如表1所示。将铰链尺寸参数分别代入式(1)和式(5)可得，keq,bend=0.193 2 N·m/rad，keq,tens=3.147 5 N·m。

表1 Nested- LET柔性铰链基本尺寸参数Tab.1 Dimensions of Nested- LET joint mm

2.2 有限元分析

2.2.1弯曲等效刚度的有限元分析

利用Abaqus有限元软件建立Nested- LET柔性铰链设计实例的有限元模型(单元类型为Shell)。当转矩为0.12 N·m时，铰链转角为0.68 rad(约为40°)时的角位移云图如图4a所示，应力云图如图4b所示。

图4 Nested- LET柔性铰链角位移及应力云图Fig.4 FEA model of Nested- LET joint showing deflected position and stress under bending condition

图5 Nested- LET柔性铰链在不同转矩下转角仿真值、理论值与修正值变化曲线Fig.5 Trend curves of simulated, theoretical and corrected bending angles of Nested- LET joint under different bending moments

由图4b可知，此时Nested- LET铰链的最大应力为1 013 MPa，小于屈服强度[sy]=1 170 MPa，因而不会发生塑性变形，满足设计要求。

Nested- LET铰链受载情况如图1所示，其力- 变形关系为

T=keq,bendθ

(16)

式中T——作用在柔性铰链上的转矩，N·m

θ——铰链扭转角理论值，rad

不同转矩作用下铰链转角仿真值、理论值曲线如图5所示。设理论计算与仿真分析的相对误差为

(17)

式中θ′——铰链扭转角仿真值，rad

根据式(17)可得到不同转矩下的相对误差，由式(17)及图5得到相对误差大于5%。

因此在弯曲等效刚度中引入修正系数α，对keq,bend进行修正，修正后等效刚度表示为

k′eq,bend=αkeq,bend

(18)

一般情况下，修正系数α会随着铰链尺寸和材料的不同而有所变化，经过大量实例分析，取修正系数α=0.9时可保证在受转矩情况下转角误差最小。修正后，不同转矩作用下铰链转角曲线如图5所示。由图5可得，Nested- LET铰链转角的仿真值与修正后的理论值基本一致，验证了Nested- LET柔性铰链弯曲等效刚度理论公式的正确性。

2.2.2拉压等效刚度的有限元分析

与弯曲刚度的有限元分析方法类似，分别对铰链施加不同的拉力。拉力为100 N时Nested- LET柔性铰链的位移变形量云图如图6所示，此时x方向位移变形量为0.037 93 mm。为保证在受拉力情况下位移误差最小，取修正系数α′=0.838，绘制不同拉力下与位移变形量仿真值、理论值与修正值曲线，如图7所示。由图7可看出，Nested- LET柔性铰链发生拉伸变形过程中产生的仿真位移变形与理论修正位移基本重合，说明修正系数α′有效。

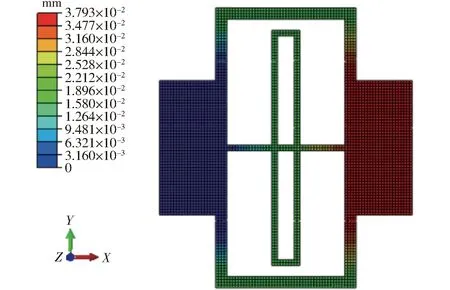
图6 Nested- LET柔性铰链位移变形量仿真云图Fig.6 Tensile deformation of Nested- LET joints obtained by FEA

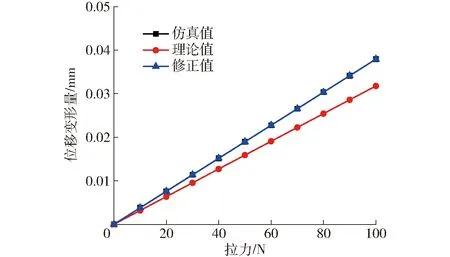
图7 Nested- LET柔性铰链在不同拉力下位移变形量理论值、修正值与仿真值变化曲线Fig.7 Trend curves of simulated, theoretical and corrected displacement deformation of Nested- LET joint under different tensions

铰链转角、位移变形仿真值均大于理论值，其误差产生的主要原因有：①为便于分析，弯曲等效刚度模型有部分简化。②建立拉压等效刚度求解方程时，均使用自由端受力的柔性悬臂梁的伪刚体模型，实际各柔性片段的边界条件存在差异性。③理论计算时，代入公式的相应片段长度为固定值，但在运动过程中，柔性铰链各片段连接处的变形为弯曲、扭转及拉压载荷共同作用产生，此部分界限的模糊性造成各片段长度为非固定值。

3 Nested- LET铰链与外LET铰链性能比较

为了进一步说明Nested- LET柔性铰链各项性能，将其与外形尺寸相同的外LET铰链进行比较。外LET铰链结构尺寸示意图如图8所示。尺寸分别为lb1=25 mm，wb1=2 mm，lt1=13 mm，wt1=2 mm。

图8 外LET铰链的结构示意图Fig.8 Structure diagram of outside LET joint

在Abaqus中建立有限元仿真模型，选取铍青铜作为材料，其弹性模量E=128 GPa，泊松比σ=0.29，屈服强度为[sy]=1 170 MPa。对Nested- LET及外LET铰链的抗拉压性能(以拉力为例)、弯曲性能和转动中心漂移进行分析比较。

图9为不同拉力作用下外LET、Nested- LET铰链的位移变形量仿真曲线，Nested- LET铰链位移变形量远小于外LET。当拉力为100 N时，外LET铰链的位移变形量为Nested- LET铰链的30倍，Nested- LET铰链的抗拉压性能得到了大幅度提升。图10为不同转矩作用下外LET、Nested- LET铰链的转角仿真值对比，Nested- LET铰链弯曲刚度增加了1.5倍，弯曲性能略有下降。

图9 不同拉力下位移变形量仿真值对比Fig.9 Comparison of displacement deformation under different tensions

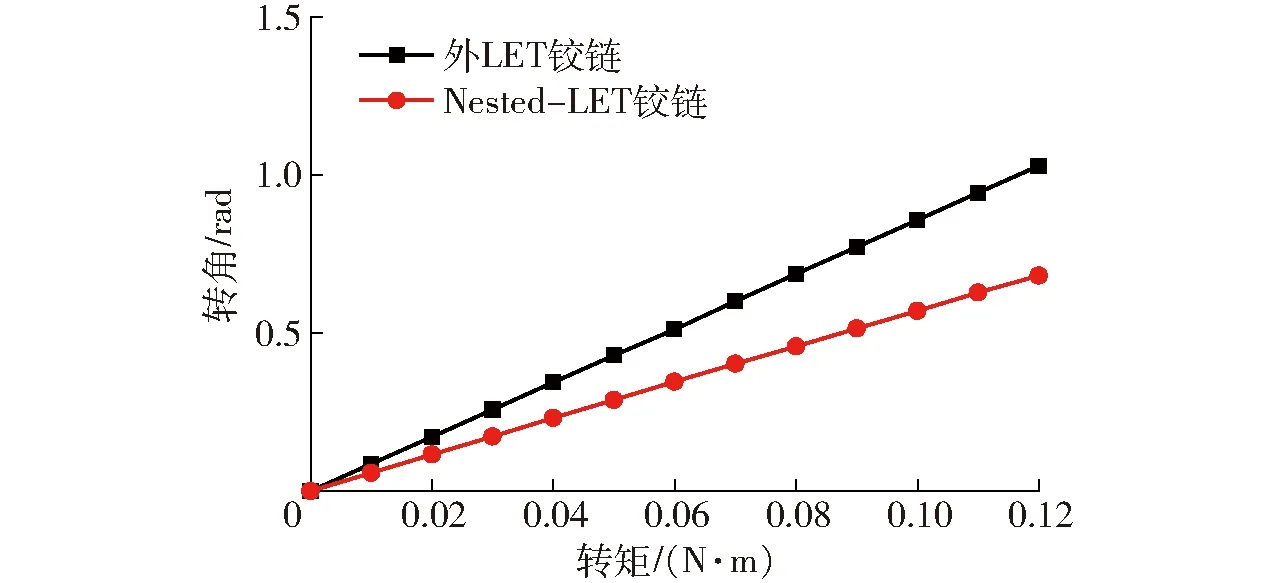
图10 不同转矩下转角仿真值对比Fig.10 Comparison of rotation angles under different bending moments

图11 柔性铰链转动中心Fig.11 Rotation center of flexure joint

转动精度是衡量柔性铰链性能的指标之一，一般用转动中心的位置表示。Nested- LET铰链为完全对称型，理想状态下转动中心位置保持在对称轴位置，但在柔性铰链发生弯曲变形的过程中，其转动并不是集中在某一点。随着转角不断地变化转动中心会发生漂移，漂移量的增加会影响转动精度，铰链弯曲变形后侧视图如图11所示。将转动中心位置标为(xc，zc)，由铰链运动特性可知zc=0，xc计算式为

(19)

式中lb1——铰链总长度

Δx——铰链转动后末端在x方向的位移

Δz——铰链转动后末端在z方向的位移

当铰链转角为30°时，由式(19)可得，外LET柔性铰链转动中心漂移量为0.405 mm，Nested- LET柔性铰链转动中心漂移量为0.352 mm，Nested- LET较好地保证了铰链在转动过程中的转动精度。

4 实验验证

为验证所设计铰链的抗拉性能，用铍青铜加工外LET和Nested- LET柔性铰链，如图12所示。由于加工制造误差，外LET铰链实际尺寸为24.97 mm×49.89 mm，Nested- LET铰链实际尺寸为24.91 mm×50.21 mm。使用UTM系列万能实验机，选择拉伸楔形夹具将铰链两端夹紧，控制该仪器对试样一端进行拉伸，实验速度为0.1 mm/min。通过力传感器实时采集试样铰链受到的拉力，结果由计算机输出。

图12 外LET、Nested- LET加工实物图Fig.12 Fabricated prototypes of outside LET and Nested- LET joints

拉伸实验台如图13a所示，图13b、13c分别为拉力为30 N时外LET铰链及Nested- LET柔性铰链的实验结果。为了更清晰地观察位移变形量，使用数显游标卡尺测量30 N拉力作用下各铰链的拉伸变形，由图13可得，外LET铰链变形量为0.43 mm，Nested- LET铰链变形量为0.02 mm，外LET变形量是Nested- LET的21.5倍。2种铰链在不同拉力作用下的仿真与实验结果如图14所示，实测与仿真结果基本一致，验证了分析的正确性，但也存在一定的误差，主要由加工制造误差、设备实验误差、测量误差等各种因素造成。实测结果进一步验证了Nested- LET铰链的抗拉性能得到了大幅度改善。

图13 外LET、Nested- LET实验结果对比Fig.13 Comparison of experimental results between outside LET and Nested- LET joints

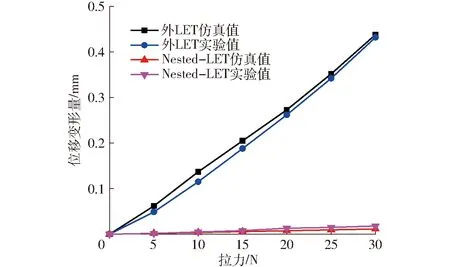
图14 外LET、Nested- LET仿真、实验结果对比Fig.14 Comparison of FEA and experimental results between outside LET and Nested- LET joints

5 结论

(1)提出了一种Nested- LET柔性铰链，设计了该柔性铰链的结构，分别对其弯曲等效刚度、拉压等效刚度进行了理论公式的推导，分析了误差产生的原因并给出对应的修正系数。通过实例的理论计算与有限元仿真分析验证了理论公式与修正系数的准确性。

(2)对Nested- LET柔性铰链与外形尺寸相同的外LET柔性铰链的性能进行了对比与分析，结果表明Nested- LET柔性铰链在弯曲性能下降不明显的情况下，拉压刚度得到很大提升，转动中心漂移量有所下降。通过对两柔性铰链进行拉伸实验验证了分析的正确性。因此，嵌套式构型的铰链能够有效改善柔性铰链的抗拉压性能，缩小转动中心漂移量，是一种精度较高的柔性铰链。

1 HOWELL L L. Compliant mechanisms [M]. New York: Wiley, 2001.

2 于靖军, 裴旭, 毕树生,等. 柔性铰链机构设计方法的研究进展 [J]. 机械工程学报, 2010, 46(13):2-13.

YU Jingjun, PEI Xu, BI Shusheng, et al. State-of-arts of design method for flexure mechanisms [J]. Journal of Mechanical Engineering, 2010, 46(13): 2-13. (in Chinese)

3 VEROTTI M, DOCHSHANOV A, BELFIORE N P. Compliance synthesis of CSFH MEMS-based microgrippers [J]. Journal of Mechanical Design, 2017, 139(2):022301-1-10.

4 ZIRBEL S A, TOLMAN K A, TREASE B P, et al. Bistable mechanisms for space applications [J]. Plos One, 2016, 11(12):e0168218.

5 HOFFMANN M, SIMANEK J. The merits of passive compliant joints in Legged locomotion: fast learning, superior energy efficiency and versatile sensing in a quadruped robot [J]. Journal of Bionic Engineering, 2017, 14(1):1-14.

6 王国彪, 陈殿生, 陈科位,等. 仿生机器人研究现状与发展趋势 [J]. 机械工程学报, 2015, 51(13):27-44.

WANG Guobiao, CHEN Diansheng, CHEN Kewei, et al. The current research status and development strategy on biomimetic robot [J]. Journal of Mechanical Engineering, 2015, 51(13):27-44. (in Chinese)

7 DODGEN E, STRATTON E, BOWDEN A, et al. Spinal implant development, modeling, and testing to achieve customizable and nonlinear stiffness [J]. Journal of Medical Devices, 2012, 6(2):021010.

8 JACOBSEN J O, CHEN G, HOWELL L L, et al. Lamina emergent torsional (LET) joint [J]. Mechanism and Machine Theory, 2009, 44(11):2098-2109.

9 WILDING S E, HOWELL L L, MAGLEBY S P. Introduction of planar compliant joints designed for combined bending and axial loading conditions in Lamina emergent mechanisms [J]. Mechanism and Machine Theory, 2012, 56:1-15.

10 DELIMONT I L, MAGLEBY S P, HOWELL L L. Evaluating compliant hinge geometries for origami-inspired mechanisms [J]. Journal of Mechanisms and Robotics, 2014, 7(1):011009.

11 MERRIAM E G, LUND J M, HOWELL L L. Compound joints: behavior and benefits of flexure arrays [J]. Precision Engineering, 2016, 45:79-89.

12 MERRIAM E G, HOWELL L L. Lattice flexures: geometries for stiffness reduction of blade flexures [J]. Precision Engineering, 2016, 45:160-167.

13 MERRIAM E G, TOLMAN K A. Integration of advanced stiffness-reduction techniques demonstrated in a 3D-printable joint [J]. Mechanism and Machine Theory, 2016, 105:260-271.

14 LIU M, ZHANG X, FATIKOW S. Design and analysis of a multi-notched flexure hinge for compliant mechanisms [J]. Precision Engineering, 2017, 48:292-304.

15 PEI X, YU J, ZONG G, et al. The modeling of cartwheel flexural hinges [J]. Mechanism and Machine Theory, 2009, 44(10):1900-1909.

16 CHEN G, SHAO X, HUANG X. A new generalized model for elliptical arc flexure hinges [J]. Review of Scientific Instruments, 2008, 79(9):095103.

17 CHEN G, LIU X, GAO H, et al. A generalized model for conic flexure hinges [J]. Review of Scientific Instruments, 2009, 80(5):055106.

18 CHEN G, LIU X, DU Y. Elliptical-arc-fillet flexure hinges: toward a generalized model for commonly used flexure hinges [J]. Journal of Mechanical Design, 2011, 133(8):081002.

19 CHEN G, WANG J, LIU X. Generalized equations for estimating stress concentration factors of various notch flexure hinges [J]. Journal of Mechanical Design, 2014, 136(3):252-261.

20 邱丽芳, 印思琪, 谢仲添,等. 基于串联式Triple- LET的LEMs滑块机构分析 [J/OL]. 农业机械学报,2016, 47(6):381-386. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160650&flag=1. DOI: 10.6041 /j.issn.1000-1298.2016.06.050.

QIU Lifang, YIN Siqi, XIE Zhongtian, et al. Analysis of lamina emergent slider mechanism based on the series Triple- LET [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6):381-386. (in Chinese)

21 邱丽芳, 王栋, 印思琪,等. Deform- X柔性铰链设计与分析 [J/OL]. 农业机械学报, 2017, 48(4):370-376. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170449&flag=1. DOI: 10.6041/j.issn.1000-1298.2017.04.049.

QIU Lifang, WANG Dong, YIN Siqi, et al. Design and analysis of Deform- X flexure hinge [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(4):370-376. (in Chinese)

22 邱丽芳, 黄钢, 陈海翔. 基于特征参数的DCA- LET结构设计与性能分析 [J/OL]. 农业机械学报, 2017, 48(8):399-404. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170848&flag=1. DOI：10.6041/j.issn.1000-1298.2017.08.048.

QIU Lifang, HUANG Gang, CHEN Haixiang. Structure design and performance analysis of DCA- LET based on characteristic parameters [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(8):399-404. (in Chinese)

23 XIE Z, QIU L, YANG D. Design and analysis of outside-deployed Lamina emergent joint (OD- LEJ) [J]. Mechanism and Machine Theory, 2017, 114:111-124.

24 CHEN G, HOWELL L L. Two general solutions of torsional compliance for variable rectangular cross-section hinges in compliant mechanisms [J]. Precision Engineering, 2009, 33:268-274.