基于离散元的微型马铃薯仿真参数标定
刘文政 何 进 李洪文 李学强 郑 侃 魏忠彩
(1.中国农业大学工学院, 北京 100083; 2.山东省马铃薯生产装备智能化工程技术研究中心, 德州 253600;3.山东希成农业机械科技有限公司, 德州 253600)
0 引言
马铃薯作为全球四大主粮作物之一,对于保障粮食安全具有重要意义[1]。种植是马铃薯生产的重要一环,其产量和质量与种薯密切相关,脱毒微型马铃薯(简称“微型薯”)是由马铃薯脱毒组织经炼苗、移栽、保护地隔离种植等培育而成,其种出的后代具有产量高、品质好、商品率高等优点[2]。为提升国内马铃薯的生产水平和经济效益,应大幅提升微型薯的种植面积和水平,其种植机械化势在必行[3]。随着计算机技术的快速发展,以离散单元法为基础的数值模拟仿真软件EDEM在农业装备研究上已得到运用[4-8]。本文以微型薯为研究对象,对其离散元仿真参数进行全面系统的研究,以促进离散元法在微型马铃薯播种装备研发中的应用。
离散元仿真时,需定义仿真模型的物性参数,主要包括本征参数(如密度、剪切模量、泊松比等)以及接触参数(如颗粒与颗粒、颗粒与材料间的弹性碰撞恢复系数、静摩擦因数、滚动摩擦因数等),其中物料本征参数与真实值基本一致,而由于颗粒仿真模型与真实颗粒在几何形态上存在差异,使得仿真接触参数与真实值存在误差,需对接触参数进行重新标定。目前这些参数主要通过直接测量和虚拟标定获取[9-10]。对离散元仿真参数的直接测量,国内外学者已做了大量研究[11-12]。然而,由于真实颗粒的各向异性,使得颗粒仿真模型与真实颗粒在外形上存在差异,直接测量数据变化差异较大,同时有些参数很难通过试验直接测量,因此,一些学者对所需的微观参数进行虚拟标定[13-15]。
目前,国内外种子颗粒标定主要集中在玉米[16-18]、水稻[19]、小麦[10]、大豆[20]等方面,而对微型薯种子颗粒进行离散元仿真参数标定方面的研究鲜有报道。微型薯相比于玉米、稻麦等在质量和形态方面均具有较大差异,其种子颗粒尺寸较大,需进行大量相关试验来探索较为复杂的运动特征。本文在现有相关研究的基础上,提出一种微型薯等大颗粒种子参数标定方法。
1 微型薯模型建立
1.1 微型薯物理模型创建
进行仿真试验时,应建立微型薯种子颗粒仿真物理模型。微型薯作为农业散体物料,其籽粒间差异性大、外形轮廓复杂,为提高离散元颗粒建模准确性,采用在EDEM软件中利用球形颗粒组合的方法建立微型薯种子仿真模型[21-22]。
微型薯选用国家马铃薯工程技术研究中心培育的质量分布在3~10 g的希森3号脱毒微型马铃薯,该品种质量好,产量高,具有微型马铃薯的典型特征。试验测定其含水率为66.97%~78.23%,平均值为73.90%;密度为1 049.60~1 085.90 kg/m3,平均值为1 077.03 kg/m3;微型薯泊松比为0.48[23],剪切模量为34.30 MPa[24]。因微型薯种子物料形态差异很大,为确定微型薯种子物理模型,随机选取500粒微型薯种子,通过游标卡尺(精度0.02 mm,量程0~150 mm)对颗粒三维尺寸(长l、宽w、厚t)进行测量,依据测量结果发现微型薯种子整体呈椭球形,根据其形态特征,引入球度Sp对微型薯颗粒进行种子形状分类,分为椭球形(Sp<0.85)和类球形(Sp>0.85)2级。其中,球度Sp为[11]
(1)

图1 微型薯分类及离散元模型Fig.1 Classification and simulation model of potato minituber
为进一步确定微型薯种子物理模型,依据测量结果对微型薯椭球形种子按照其长轴尺寸是否大于35 mm分为2级,即微型薯种子颗粒共分为椭球小粒、椭球大粒和类球形(图1a),且数量比为20∶4∶1。为便于在EDEM中建立微型薯种子颗粒模型,对于椭球形种子而言,设定其长轴长度a=l,短轴长度b=(w+t)/2;对于类球形种子而言,其直径d=(l+w+t)/3。由此得椭球小粒种子平均长轴长度为29.20 mm,平均短轴长度为18.24 mm;椭球大粒种子平均长轴长度为39.32 mm,平均短轴长度为20.54 mm;类球形种子平均直径为20.46 mm。根据上述测量结果,在EDEM的原型颗粒模型创建中利用多球面组合功能建立椭球大粒、椭球小粒及类球形微型薯种子颗粒离散元模型,如图1b所示。
1.2 微型薯接触模型选取
试验过程中,微型薯除了颗粒间的接触,还会与其他材料接触产生力的作用。本文试验接触材料选用农业装备中常用的Q235钢制材料,其密度为7 850 kg/m3,泊松比为0.28,剪切模量为8.20×104MPa[25]。
在仿真过程中,微型薯颗粒模型作为离散体具有真实微型薯种子颗粒的几何和物理两类基本特征,采用离散元方法模拟微型薯仿真颗粒的运动过程。在开展相关仿真试验时,依据微型薯物料特性,其表面粘附力较小,且假设颗粒在运动过程中位移、力、速度等参数的变化是通过颗粒间或颗粒与接触材料之间产生的微小交叠量的不同来确定的,根据牛顿第二定律,每个微型薯颗粒模型在力和扭矩的作用下发生运动和旋转。基于以上假设,微型薯颗粒的相关运动过程采用Hertz- Mindlin无滑动接触力学模型[26-29]。
基于该模型,微型薯颗粒在颗粒间或颗粒- 材料间所受法向力Fn和切向力Ft满足函数关系式
(2)
式中E*——等效弹性模量
R*——等效接触半径
δn——法向重叠量
δt——切向重叠量
St——切向刚度
微型薯颗粒间或颗粒- 材料间法向阻尼力Fn,d及切向阻尼力Ft,d满足
(3)
式中β——阻尼比m*——等效质量
Sn——法向刚度
υn,rel——法向相对速度
υt,rel——切向相对速度
微型薯颗粒间或颗粒- 材料间的切向力Ft还受库伦摩擦力μsFn限制,其中μs为静摩擦因数。微型薯仿真颗粒在运动中不可避免受到滚动摩擦力的影响,而滚动摩擦可以通过接触表面上的力矩Ti来说明,其中,力矩Ti与滚动摩擦因数μr、颗粒质心至接触点间距Ri、颗粒在接触点处的角速度ωi存在关系
Ti=-μrFnRiωi
(4)
式中μr为无量纲参数,该参数值的不同会影响颗粒阻抗滚动程度的大小。
2 微型薯离散元参数获取模型
2.1 微型薯碰撞恢复系数测定模型
碰撞恢复系数是表征物体碰撞时变形恢复能力的参数,为碰撞前后的两物体在接触点处的法向相对分离速度与法向相对接近速度之比[30]。根据碰撞恢复系数物理学定义建立其测定模型,分别对微型薯- 钢板、颗粒间碰撞恢复系数进行分析和标定。
2.1.1微型薯- 钢板碰撞恢复系数
利用微型薯颗粒的碰撞弹跳试验对微型薯- 钢板碰撞恢复系数进行测定[26],整个运动过程由高速摄像机(美国Vision Research公司,Phantom v 9.1)采集记录,如图2a所示。微型薯- 钢板碰撞恢复系数可表示为颗粒与钢板碰撞前后在碰撞接触点处的法向方向瞬时分离速度v1与瞬时接触速度v0之比,计算公式为
(5)
式中H0——微型薯颗粒下落高度
H1——微型薯颗粒与钢板碰撞反弹最大高度

图2 微型薯- 钢板碰撞恢复系数测定试验Fig.2 Measurement test of potato minituber- steel plate coefficient of restitution
试验选取类球形微型薯种子颗粒从一定高度H0释放,使其跌落至水平放置的钢板上,用高速摄像机采集到种子颗粒弹起的最高点,通过坐标纸读取该点的高度H1(H1 试验中选取已建立的类球形微型薯颗粒仿真模型,颗粒以初速度零且距离水平放置的钢板450 mm处做自由落体运动。在微型薯- 钢板仿真接触参数中,静摩擦因数、滚动摩擦因数对颗粒反弹高度无影响,为避免干扰将这两个参数设为零;参照真实试验测定的微型薯- 钢板碰撞恢复系数取值范围,设定微型薯- 钢板仿真碰撞恢复系数在0.485~0.570范围内取值,并通过EDEM离散元分析模块对相应颗粒反弹高度进行测定(图2b),经过预仿真试验确定仿真试验设计方案与结果如表1所示。以恢复系数x1为试验因素,反弹高度y1为评价指标,对结果进行曲线拟合,建立拟合方程 (6) 表1 微型薯- 钢板碰撞恢复系数仿真试验方案与结果Tab.1 Simulation test plan and results of potatominituber- steel plate coefficient of restitution 决定系数R2=0.999 9,该值接近1,表明拟合方程可靠度高。将y1=124.80 mm代入方程(6)得x1=0.523,设定微型薯- 钢板恢复系数为0.523并分别在H0为400、450、500 mm仿真试验条件各做3次重复仿真试验,得颗粒平均仿真反弹高度H′1分别为113.233、124.778、139.987 mm,取平均值124.810 mm,与真实试验条件得到的反弹高度相对误差分别为1.53%、0.008%、1.93%。由此表明标定后的仿真结果与试验结果基本吻合,故选取颗粒- 钢板仿真恢复系数为e′w1=0.523。 通过标定后的微型薯- 钢板仿真碰撞恢复系数e′w1=0.523,真实试验测量中测定ew1=0.526,两者相对误差仅为0.57%,发现标定后的微型薯- 钢板仿真碰撞恢复系数与真实试验条件下测定的结果十分接近,其原因可能在于微型薯颗粒在与钢板碰撞过程中因接触时间极短、瞬间碰撞力极大,利用仿真进行模拟的物理环境条件与真实试验条件趋于一致,故通过仿真标定的颗粒- 钢板碰撞恢复系数与真实试验条件所测值出现了近乎相等的情况;同时,在真实试验中通过对不同高度微型薯开展碰撞恢复系数测定试验发现,随着释放高度的增加,所得恢复系数虽变化不大但相应地会略有减小,分析其原因可能在于微型薯释放高度越高其与钢板碰撞时变形量越大,颗粒所需恢复时间就越长,而此时颗粒与钢板接触时间极短,微型薯颗粒因变形较大消耗较多能量,进而导致恢复系数值的降低。 2.1.2微型薯颗粒间恢复系数 为测定微型薯颗粒间碰撞恢复系数,引入两颗类球形微型薯进行碰撞试验[26],如图3a所示,其中颗粒a与颗粒b分别用尼龙绳套接,尼龙绳另一端固结于角钢上,角钢挂接在墙体上,并保证在颗粒自然悬垂状态下,颗粒a、b处于同一高度且均在尼龙绳的束缚下做半径r=640 mm的摆动。试验过程中,以颗粒a、b 自然悬垂点为基点,提升颗粒a(保持尼龙绳处于拉伸状态)至基点垂直方向高度H0,本试验分别设定H0为80、100、120 mm,颗粒b自然悬垂并保持静止。以初速度为零释放颗粒a,运动至最底端与颗粒b发生碰撞,颗粒a、b均绕着尼龙绳摆动至最高点,此时在垂直方向,颗粒a、b距基点高度分别为Ha、Hb,整个过程由高速摄像机记录。根据碰撞恢复系数物理学定义得微型薯颗粒间碰撞恢复系数计算公式为 (7) 式中v1——碰撞前瞬间颗粒a瞬时速度 v′——碰撞后瞬间颗粒a瞬时速度 v0——碰撞后瞬间颗粒b瞬时速度 颗粒a在H0为80、100、120 mm等条件下各进行30次重复碰撞试验得Ha为(5.01±1.48) mm、(5.93±2.08) mm、(6.56±1.70) mm,Hb为(43.01±6.75) mm、(52.67±11.55) mm、(60.46±8.94) mm,仿真过程中分别对应选取Ha为5.01、5.93、6.56 mm,Hb为43.01、52.67、60.46 mm作为验证值,得颗粒a在3种释放高度下微型薯颗粒间恢复系数ew2依次为0.483±0.009、0.480±0.011、0.476±0.007。由此表明,改变颗粒a初始释放高度对于获取微型薯颗粒间碰撞恢复系数值无显著影响,故选取H0=100 mm作为初始条件开展标定仿真试验,此条件下测得ew2取值范围为0.131~0.589。 图3 颗粒间恢复系数测定试验Fig.3 Measurement test of particle- particle coefficient of restitution 考虑到在EDEM软件中模拟微型薯颗粒在绳的束缚下摆动难度较大,仿真试验采用等效颗粒碰撞模型,即仿真颗粒通过半径r1=640 mm的半圆形管道进行约束,且穿过管道中心线的平面与水平面垂直,管道内径D2=10.50 mm,如图3b所示。仿真过程中选取类球形微型薯颗粒仿真模型,分别在距轨道最低点垂直高度为100 mm的管道位置处及轨道最低点各生成1粒微型薯颗粒模型a、b且均保持静止。经预仿真试验发现,管道本征参数对颗粒碰撞过程影响不显著,将管道本征参数参照钢板设定,并将微型薯- 管道接触参数中的碰撞恢复系数、静摩擦因数、滚动摩擦因数均设定为0。以初速度为0释放微型薯颗粒a,模拟颗粒间碰撞过程,并利用EDEM软件分析模块求出两颗粒碰撞后上升的最大高度Ha、Hb,经过预仿真试验并结合真实颗粒碰撞试验条件下测得的颗粒间恢复系数ew2取值范围确定试验方案并得出结果(表2)。以微型薯颗粒间碰撞恢复系数x为试验因素,颗粒a、颗粒b碰撞后上升最大高度ya、yb为评价指标,对结果进行曲线拟合,得拟合方程 (8) 表2 颗粒间碰撞恢复系数仿真试验方案与结果Tab.2 Simulation test plan and results of particle- particlecoefficient of restitution 通过标定后的颗粒间仿真碰撞恢复系数e′w2=0.478,真实试验测量中得ew2=0.480,两者相对误差为4.17%,发现标定后的颗粒间仿真碰撞恢复系数与真实试验条件下测定的结果差异较小,其原因可能在于微型薯颗粒与颗粒间的碰撞过程因接触时间极短、瞬间碰撞力极大,同时微型薯颗粒内部具有相对较均匀的密度及质量分布,利用仿真进行模拟的物理环境条件与真实试验条件趋于一致,故通过仿真标定的颗粒间碰撞恢复系数与真实试验条件所测值出现了差异较小的情况。 建立微型薯- 钢板摩擦因数测定模型,依据能量守恒定律,利用斜面滑动法、滚动法分别对微型薯- 钢板静摩擦因数和滚动摩擦因数进行分析和标定。 2.2.1微型薯- 钢板静摩擦因数 斜面滑动法是测量静摩擦因数常用方法,质量为m的物体重力分解为2个力:平行于斜面的力F(N)和垂直于斜面的力T(N)。当斜面倾角α(°)小于滑动临界角时,F小于物体与斜面间的静摩擦力f(N),物体保持静止,随着斜面角度α的增加,F值越来越大,当α大于物体滑动临界角时,F>f,物体将开始沿着斜面下滑。其中,静摩擦因数μs与斜面倾角α的关系为 μs=f/T=mgsinα/(mgcosα)=tanα (9) 试验中取一张Q235钢制平板作为试验斜面,为防止单粒微型薯在斜面上滚动,将4颗类球形微型薯颗粒粘结在一起(半径r=10 mm)放置在平板上(图4a),平板一侧与水平试验台始终贴合并保持不动,缓慢匀速地将平板另一侧抬起,当微型薯在平板上开始滑动时,利用数显角度尺(精度0.05°,量程0°~360°)测量平板与试验台的夹角θ,重复试验30次,取平均值得θ=(32.80±0.05)°,仿真过程中选取θ=32.80°,通过试验测定微型薯- 钢板静摩擦因数μs1=0.646±0.058。 图4 颗粒- 钢板静摩擦因数测定试验Fig.4 Measurement test of potato minituber- steel plate coefficient of static friction1.组合颗粒 2.钢制平板 在EDEM软件中添加1个方形平板(长400 mm、宽500 mm),设置其本征参数与Q235钢板相同,并采用多球面组合方法生成4球组合微型薯仿真颗粒以模拟真实试验条件下的粘结微型薯颗粒(图4b)。在离散元仿真过程中,微型薯- 钢板间仿真接触参数设定如下:碰撞恢复系数选取已标定值0.523,滚动摩擦因数取值为0以消除其对斜面滑动仿真试验的影响。通过改变方形平板的倾斜角度,在对应每个倾斜角度下通过二分法确定颗粒- 钢板静摩擦因数,试验方案与结果如表3所示。以颗粒- 钢板静摩擦因数x2为试验因素,倾斜角度y为评价指标,对试验结果进行曲线拟合,得回归方程 (10) 方程的决定系数R2=1,表明回归方程准确有效。将y=32.80°代入方程(10)得x2=0.644,并以颗粒- 钢板静摩擦因数为0.644进行3次重复斜面滑动仿真试验,得钢制平板倾斜角度分别为32.75°、32.78°、32.78°,取平均值32.77°,与试验所得钢制平板倾斜角度相对误差为0.09%。由此表明标定后的仿真结果与试验结果基本一致,故选取微型薯- 钢板静摩擦因数μ′s1=0.644。 耳石症是一种当头部快速移动时出现眩晕和位置性眼震的眩晕症,发病率随年龄增长,且女性发病率高于男性,严重影响患者生活质量。关于耳石症的发病机理,目前主流观点认为是由于耳石变形脱落(可能由重大外力撞击或衰老导致)移动到其它平衡器官造成眩晕。临床上常采用手法复位来使耳石复位进行治疗,Epley手法复位和Barbecue翻滚手法复位是当前临床上较为常见的用于治疗耳石症的复位手法,Epley手法复位通过移动患者头部,在重力的作用下使耳石复位,Barbecue翻滚手法复位是根据耳石假说和前庭结构解剖学关系来移动患者头部使耳石复位。 表3 微型薯- 钢板静摩擦因数仿真试验方案与结果Tab.3 Simulation test plan and results of potatominituber- steel plate coefficient of static friction 通过标定得微型薯- 钢板静摩擦因数μ′s1=0.644,真实试验条件下测得μs1=0.646,两者相对误差仅为0.31%,发现标定后的微型薯- 钢板静摩擦因数与真实试验条件下测定的结果差异较小,经分析其原因可能在于通过斜面法测定微型薯- 钢板静摩擦因数,试验过程中微型薯颗粒受到重力和静摩擦力的共同作用始终与钢板表面保持贴合,当钢板斜面倾角达到滑动临界角时,微型薯颗粒开始沿着斜面下滑,整个过程并没有滚动摩擦力作为混合摩擦力的影响因素,颗粒受力相对单一,利用仿真模拟所创造的物理环境条件与真实试验条件趋于一致,故通过仿真标定颗粒- 钢板静摩擦因数与真实试验条件所测值基本一致。 2.2.2微型薯- 钢板滚动摩擦因数 滚动摩擦是指当一个物体在另一物体表面作无滑动的滚动或有滚动的趋势时,由于物体在接触部分受压发生形变而产生阻碍滚动的作用,其一般用阻力矩来度量,力的大小与物体的性质、表面形状以及滚动物体的质量有关[11]。微型薯颗粒在钢制平板上的滚动将产生滚动摩擦,试验分别选取椭球形微型薯颗粒(长轴长度29 mm、短轴长度18 mm)和类球形微型薯颗粒(半径10 mm)为试验对象,从一定倾斜角度β的钢制平板上在某一位置以初速度为0沿着斜面向下滚动(颗粒在斜面上的滚动距离为S),并最终滚落至水平放置的钢制平板上,由于受到滚动摩擦,微型薯颗粒在水平钢板上滚动一段距离之后最终静止,采用卷尺测定颗粒在水平钢板上的滚动距离L,以L为评价指标,对微型薯- 钢板滚动摩擦仿真系数进行标定(图5a)。试验过程中,假设所选取的微型薯种子为理想的椭球和圆球颗粒,微型薯颗粒做的是纯滚动故认为其所受阻力仅为滚动摩擦力而不考虑滚动过程中静摩擦力的影响,由能量守恒定律得[31] mgSsinβ=μrmg(Scosβ+L) (11) 通过预滚动试验发现,当斜置钢板倾斜角度β过小时,因选取的微型薯并不是理想的椭球或圆球,颗粒在斜面上无滚动或滚动一段距离S之后将静置停留在斜面上;当斜置钢板倾斜角度β过大时,颗粒滚落至平行放置的钢板上时将产生弹跳,影响试验结果,综合考虑,本试验选取斜置钢板倾斜角度β=20°。同时,微型薯在斜置钢板上运行距离S不能过小也不能过大,当斜向运行距离S过小时,颗粒滚落至水平钢板上水平速度太小导致水平滚动位移L过短,不利于试验测量;当斜向运行距离S过大时,颗粒滚落至水平钢板上速度较大导致水平滚动位移L较长,由于微型薯颗粒不是理想的椭球体或圆球体,颗粒水平运行轨迹将不能保证在一条直线上,因此为提升试验的可靠性及准确性,经过预试验,设定颗粒在斜面上滚动距离S=50 mm。通过大量预试验发现两类微型薯颗粒滚动距离基本一致,但由于椭球形微型薯颗粒因形状及质量分布不均,在滚动过程中极易出现运动轨迹不在同一条直线且轨迹线较复杂的现象,综合考虑,本文以类球形微型薯为试验对象开展微型薯- 钢板滚动摩擦因数标定仿真试验。根据上述试验要求,进行30次重复滚动测量试验,取平均值得颗粒在水平钢板上的滚动距离为L=639 mm。将上述测定值代入式(11)中,得真实试验条件下微型薯- 钢板滚动摩擦因数μr1=0.010 8。 图5 颗粒- 钢板滚动摩擦因数测定试验Fig.5 Measurement test of particle- steel plate coefficient of rolling friction1.倾斜钢板 2.平置钢板 3.微型薯颗粒 4.卷尺 在离散元仿真中,通过EDEM软件分别添加倾斜放置(角度20°)和水平放置的矩形平板,且倾斜放置的平板底端与水平放置的平板相接触,设置两平板的本征参数与Q235钢相同,沿着倾斜平板面向上距离底端S=50 mm处生成一半径r=10 mm的球形微型薯仿真颗粒并以初速度为0沿着斜面向下滚动(图5b)。颗粒在实际滚动过程中同时受到静摩擦的作用,故在仿真模拟中微型薯- 钢板接触参数如下:碰撞恢复系数、静摩擦因数均选取上文标定值e′w1=0.523、μ′s1=0.644。经预仿真试验得出微型薯- 钢板滚动摩擦因数取值范围为0.020 0~0.027 0,仿真试验方案与结果如表4所示。以微型薯- 钢板滚动摩擦因数x3为试验因素,以微型薯仿真颗粒在水平平板上的滚动距离L为评价指标,对结果进行曲线拟合,建立拟合方程 (12) 方程决定系数R2=0.999 9,接近1,表明拟合方程准确可靠。将L=639 mm代入方程(12)得x3=0.022 1,设定微型薯- 钢板滚动摩擦因数为0.022 1并在试验对象为椭球形和类球形微型薯仿真颗粒两种条件下各进行3次重复斜面滚动仿真试验,得微型薯仿真颗粒在水平放置的平板上平均滚动距离分别为627 mm和638 mm,与试验所得微型薯在水平钢板上的滚动距离相对误差各为1.88%、0.16%。由此表明标定后的仿真结果与试验结果基本一致,故选取微型薯- 钢板仿真滚动摩擦因数为μ′r1=0.022 1。 表4 微型薯- 钢板滚动摩擦仿真试验方案与结果Tab.4 Simulation test plan and results of potatominituber-steel plate coefficient of rolling friction 通过标定得微型薯- 钢板间仿真滚动摩擦因数μ′r1=0.022 1,真实试验测定得μr1=0.010 8,两者相对误差高达104.63%,发现标定后微型薯- 钢板间滚动摩擦因数与真实试验条件测定值差异较大,分析其原因可能是:①真实微型薯颗粒并不是理想的椭球或圆球体,在真实试验条件下并不能保证颗粒在滚动过程中其运行轨迹为一条直线,用卷尺测定其滚动距离存在误差,同时所选取的微型薯颗粒表皮以及钢板表面特性与仿真模型有所差异。②在真实试验条件下微型薯颗粒重力势能的损耗并不只是来自滚动摩擦,还应包括颗粒- 钢板间所产生的静摩擦以及颗粒在滚动过程中与钢板碰撞所损耗的能量,而仿真条件下所设定的则是理想的物理环境条件,即仿真模拟的环境条件与真实试验条件差异较大,故出现标定值与真实试验值相对误差较高的情况。 堆积角是表征颗粒物料流动、摩擦等特性的宏观参数,其中静摩擦因数、滚动摩擦因数等接触参数对结果影响显著[22,31-33],上文已对微型薯- 钢板静摩擦因数、滚动摩擦因数等仿真参数进行了标定,本试验模型则用来对微型薯颗粒间静摩擦因数、滚动摩擦因数等仿真参数进行分析和标定。 2.3.1堆积角测量试验 采用箱体抽板法进行试验[31,34](图6a),测量装置(Q235钢制材料)由箱体(长400 mm、宽300 mm、高500 mm)、挡板(长400 m、高500 mm)和底板(长1 000 mm、宽1 000 mm)组成,为使颗粒种子在堆积过程中充分扩散并在水平底板上形成无约束颗粒堆,应以较缓慢的速度向上抽提挡板[35],设定向上抽提速度为0.05 m/s,待种群稳定后,颗粒种群所形成的斜面与水平底板平面的夹角即为种群堆积角,试验重复10次。 图6 箱体测量装置Fig.6 Measurement device with box1.挡板 2.箱体 3.种子 4.底板 图7 堆积角图像处理Fig.7 Image analysis by Matlab for stacking angle 堆积角试验所采集的图像,利用Matlab进行处理,因微型薯种子颗粒较大,应依次对图像进行灰度处理、二值化处理、孔洞填充、提取边界曲线,最后利用最小二乘法对边界曲线进行直线拟合,如图7所示,其中横纵坐标分别为图像水平像素点和垂直像素点,不具有实际量纲,拟合的直线斜率即为堆积角正切值,将正切值转化为堆积角,由此得堆积角均值为(26.32±1.20)°,试验中堆积角目标值选取26.32°。 2.3.2仿真参数分析和标定 进行仿真试验时,以建立的微型薯仿真模型为基准,为避免生成过小的颗粒,根据实际测得的微型薯颗粒最小、最大尺寸,将单元球半径限制在0.8~1.2倍的初始半径之间。此外,由于应力波在微型薯颗粒中传播受仿真参数的影响,各仿真中瑞利时步可能不同,因此在所有仿真中统一取20%瑞利时步。仿真中网格尺寸取3倍最小球形单元尺寸[23,36-37]。堆积角仿真试验通过改变颗粒间静摩擦因数、滚动摩擦因数,对堆积角进行标定,其它离散元仿真参数均采用上述所确定的经验值和标定参数,如表5所示。 表5 离散元仿真参数Tab.5 Parameters of discrete element simulation 将箱体测量装置的Solidworks三维几何模型转换成.stp格式文件并导入EDEM中,以确保仿真中试验装置与实际试验中所用试验装置保持一致;创建3个颗粒工厂,分别生成椭球小粒、椭球大粒、类球形3类微型薯颗粒,该颗粒工厂为虚拟表面(长400 mm,宽300 mm),生成后的颗粒以0.5 m/s的速度下落并充满上述试验箱体内,直至达到稳定状态,设置颗粒生成时间为3 s、生成方式为Dynamic,对于椭球小粒、椭球大粒及类球形3类微型薯颗粒,其生成速率分别为4 000、800、200颗/s。颗粒生成后,在EDEM中以0.05 m/s的速度垂直向上提升挡种板,种子颗粒将从箱体底端缓慢流出,最终在水平放置的钢制底板上形成稳定的颗粒堆,为确保颗粒堆达到稳定状态,将仿真运行时间设定为10 s(图6b)。稳定的颗粒堆形成之后,运用Matlab对堆积角图像进行处理并读取角度值。 经过大量预仿真试验,确定微型薯颗粒间静摩擦因数仿真值范围0.300~0.325,颗粒间滚动摩擦因数仿真值范围0.030 0~0.032 6,应用Design-Expert软件进行通用旋转中心组合试验设计,选取微型薯颗粒间静摩擦因数和滚动摩擦因数为试验因素,堆积角和仿真时间为评价指标,设置的仿真试验因素编码如表6所示。 表6 仿真试验因素编码Tab.6 Coding of factors 试验方案及结果如表7所示,A、B为因素编码值。其中仿真时间是指堆积角仿真试验时从运行开始至颗粒堆达到稳定状态的时间,选用仿真时间作为评价指标是考虑到不同的试验组合运行时间有所差异,仿真运行时间越长表明仿真耗散的时间越多,同时生成的仿真文件所占存储空间越大,本仿真试验设定全部颗粒的平均速度小于1.0×10-4m/s时颗粒堆达到稳定状态,找出这一时间点即为模拟仿真时间。 表7 仿真试验方案设计与结果Tab.7 Simulation experiment plan and result 利用Design-Expert 8.0.6软件对仿真试验结果进行方差分析,发现两试验模型均为极显著(P<0.01),说明此试验合理有效。对指标有显著影响的所有因素均已考虑到,得出拟合较好且具有实际分析意义的因素编码值的回归方程[38] (13) 利用Design-Expert 8.0.6软件的优化模块,使仿真结果最接近试验所得的微型薯颗粒堆积角,对回归模型进行有约束目标的优化求解[39]。 在优化模块的条件设置中对两评价指标的重要程度进行设定,其中堆积角设定为“+++++”,仿真时间设定为“+”。由此得到优化结果为:微型薯颗粒间静摩擦因数为μ′s2=0.325,微型薯颗粒间滚动摩擦因数为μ′r2=0.030 0,此时堆积角仿真结果为θ=26.32°,仿真时间为t=5.466 36 s。 将标定后的颗粒间摩擦因数代入EDEM软件中进行3次重复堆积角仿真试验,得堆积角分别为26.16°、26.39°、26.45°,取平均值26.33°,与试验测量值相对误差为0.04%;仿真时间分别为5.250 01、5.250 01、5.250 01 s,取平均值5.250 01 s,小于优化结果所得的仿真时间5.466 36 s。由此表明标定的仿真结果与试验结果基本吻合,故微型薯颗粒间静摩擦因数、微型薯颗粒间滚动摩擦因数的仿真参数标定值分别为μ′s2=0.325、μ′r2=0.030 0。 采用堆积角试验对微型薯颗粒间静摩擦因数和滚动摩擦因数进行标定而不同于上述颗粒- 钢板摩擦因数模型中利用斜面滑动与滚动法对其参数进行试验测量与仿真模拟相结合的方法来标定,是由于考虑到微型薯种子颗粒形状不规则,种子表面有凹凸,在进行相关测定时会产生太多干扰因素,直接测定微型薯颗粒间相关摩擦因数误差太大,故利用颗粒种群堆积角等宏观现象来表征其相关物理特性。 采用无底圆筒提升法进行堆积角验证试验[13,17,34](图8a),测量装置(Q235钢制材料)由无底圆筒(内径250 mm、高度750 mm)和底板(长1 000 mm、宽1 000 mm)组成,以0.05 m/s速度向上提升圆筒,待微型薯颗粒种群稳定后,测定颗粒种群所形成的斜面与水平底板平面的夹角即为种群堆积角,试验所采集的图像利用Matlab进行处理,试验重复10次,求得堆积角平均值为(23.96±1.15)°,其目标值取23.96°。将上述标定获取的离散元本征参数和接触参数输入EDEM中进行无底圆筒提升法堆积角仿真试验(图8b),其中参数设定方法同2.3.2节,重复仿真试验3次,测定结果为:24.10°、25.88°、22.39°,求均值得(24.12±1.75)°,取值24.12°与试验得到的堆积角相对误差为0.67%,表明标定后的仿真结果与试验结果基本吻合,由此说明通过标定的方法可以找到仿真模型与试验微型薯颗粒间在物理特性上的对应关系,根据等效原则建立了仿真与实际试验之间的联系。 图8 圆筒测量装置Fig.8 Measurement device with steel cylinder1.无底圆筒 2.底板 3.种子 图9 落种试验Fig.9 Falling seeds test1.种箱 2.振动排序单元 3.落种单元 4.开沟单元 为进一步验证参数的准确性及适用性,选用一款微型马铃薯振动排序播种装置(图9a)进行落种试验。该播种装置主要由种箱、振动排序单元、落种单元以及开沟单元构成,其工作原理为微型薯种子从种箱排种口排出并落至振动排序单元,微型薯在以周期性振动的振动排序单元作用下实现薯种的单列排序并输送至落种单元。落种单元将单列排序的薯种播落至开沟单元所开的种沟内,完成整个播种过程。其中种箱和振动排序单元均由Q235钢制材料制成。本文在真实试验条件下将1500粒微型薯倒入种箱内,薯种颗粒从种箱排种口排出至振动排序播种单元内,并设置振动排序单元进行3个周期的振动,待种群稳定后观察微型薯颗粒分布情况(图9b)。依据真实试验相关参数进行微型薯仿真落种试验(图9c),两种条件下均做3次重复试验。选取落入播种单元内的颗粒数量m、颗粒种群在落种口形成的堆积角α作为种子分布情况的2个关键特征进行对比,测量值如表8所示。 表8 真实试验与仿真种群关键特征参数对比Tab.8 Comparison of key feature parameters foractual and simulation results 结果表明测得播种单元内的颗粒数量在仿真与真实试验条件下的种量相对误差为4.4%;微型薯种群堆积角在仿真与真实试验条件下的堆积角相对误差为4.8%。仿真条件下微型薯颗粒分布情况与真实试验条件基本相同,说明通过标定后的相关微型薯颗粒种子物性参数可以应用于离散元仿真中,为后续仿真模拟提供基础。 (1)以微型薯种子作为研究对象,创建微型薯模型,以此为基础建立微型薯离散元参数获取模型,利用试验与仿真模拟相结合的方法,根据各仿真接触模型的相关试验数据进行回归分析,建立回归方程,依次求取微型薯- 钢板碰撞恢复系数为0.523,微型薯颗粒间碰撞恢复系数为0.478,微型薯- 钢板静摩擦因数为0.644,微型薯- 钢板滚动摩擦因数为0.022 1,微型薯颗粒间静摩擦因数为0.325,微型薯颗粒间滚动摩擦因数为0.030 0。 (2)采用无底圆筒提升法进行堆积角试验、采用落种法观察微型薯颗粒种群分布情况,对离散元仿真参数进行验证,结果为采用无底圆筒提升法获取堆积角为24.12°,相对误差为0.67%;落种法观察颗粒种群分布情况,对比2个关键特征,其数值相对误差均在4.80%以内。由此表明该方法可全面、系统地找到微型薯颗粒离散元仿真参数,从而为微型马铃薯相关播种机具设计和优化提供了理论依据。 1 NIEDERHAUSER J S. International cooperation and the role of the potato in feeding the world[J]. American Potato Journal,1993,70(5): 385-403. 2 张勇,李丽霞,韩宏宇,等. 马铃薯微型原种播种机的研究现状与展望[J]. 安徽农业科学,2015,43(4): 372-375. 3 吕金庆,杨颖,李紫辉,等. 舀勺式马铃薯播种机排种器的设计与试验[J]. 农业工程学报,2016,32(16): 17-25. LÜ Jinqing, YANG Ying, LI Zihui, et al. Design and experiment of cup-belt type potato seed-metering device[J]. Transactions of the CSAE, 2016,32(16): 17-25. (in Chinese) 4 王云霞,梁志杰,崔涛,等. 玉米分层施肥器结构设计与试验[J/OL]. 农业机械学报,2016,47(增刊): 163-169. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=2016s025&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.S0.025. WANG Yunxia, LIANG Zhijie, CUI Tao, et al. Design and experiment of layered fertilization device for corn[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(Supp.): 163-169. (in Chinese) 5 闫银发,孟德兴,宋占华,等. 槽轮式补饲机颗粒动力学数值模拟与试验[J/OL]. 农业机械学报,2016,47(增刊): 249-253. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=2016s038&flag=1&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2016.S0.038. YAN Yinfa, MENG Dexing, SONG Zhanhua, et al. Particle kinetic simulation and experiment for flute-wheel feeding machine[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(Supp.): 249-253. (in Chinese) 6 刘月琴,赵满全,刘飞,等. 基于离散元的气吸式排种器工作参数仿真优化[J/OL]. 农业机械学报,2016,47(7): 65-72. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160710&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.07.010. LIU Yueqin, ZHAO Manquan, LIU Fei, et al. Simulation and optimization of working parameters of air suction metering device based on discrete element[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7): 65-72. (in Chinese) 7 黄玉祥,杭程光,苑梦婵,等. 深松土壤扰动行为的离散元仿真与试验[J/OL]. 农业机械学报,2016,47(7): 80-88. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160712&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.07.012. HUANG Yuxiang, HANG Chengguang, YUAN Mengchan, et al. Discrete element simulation and experiment on disturbance behavior of subsoiling[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7):80-88. (in Chinese) 8 LENAERTS B, AERTSEN T, TIJSKENS E, et al. Simulation of grain-straw separation by discrete element modeling with bendable straw particles [J]. Computers & Electronics in Agriculture, 2014, 101(2): 24-33. 9 MARTINA C L, BOUVARDA D, SHIMAB S. Study of particle rearrangement during powder compaction by the discrete element method[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(4): 667-693. 10 刘凡一,张舰,李博,等. 基于堆积试验的小麦离散元参数分析及标定[J]. 农业工程学报,2016,32 (12): 247-253. LIU Fanyi, ZHANG Jian, LI Bo,et al. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap[J]. Transactions of the CSAE, 2016, 32(12): 247-253. (in Chinese) 11 崔涛,刘佳,杨丽,等. 基于高速摄像的玉米种子滚动摩擦特性试验与仿真[J]. 农业工程学报,2013,29(15): 34-41. 13 王宪良,胡红,王庆杰,等. 基于离散元的土壤模型参数标定方法[J/OL]. 农业机械学报,2017,48(12): 78-85. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20171209&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2017.12.009. WANG Xianliang, HU Hong, WANG Qingjie, et al. Calibration method of soil contact characteristic parameters based on DEM theory[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12): 78-85. (in Chinese) 14 李守巨,李德,于申基. 基于宏观实验数据的堆石料细观本构模型参数反演[J]. 山东科技大学学报: 自然科学版,2015,34(5): 20-26. 15 CAMPOS A V P, OLIVEIRA O S, FERREIRA L V, et al. Dem simulations of dynamic angle of repose of acerola residue: a parametric study using a response surface technique[J]. Blucher Chemical Engineering Proceedings, 2015, 1(2): 11326-11333. 16 WANG X, YU J, LV F, et al. A multi-sphere based modelling method for maize grain assemblies[J]. Advanced Powder Technology, 2017, 28(2):584-595. 17 WANG L, LI R, WU B, et al. Determination of the coefficient of rolling friction of an irregularly shaped maize particle group using physical experiment and simulations[J]. Particuology, 2018,38:185-195. 18 COETZEE C J, DNJ E. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling[J]. Computers & Electronics in Agriculture, 2009, 65(2): 198-212. 19 邱白晶,姜国微,杨宁,等. 水稻籽粒流对承载板冲击过程离散元分析[J]. 农业工程学报,2012,28(3): 44-49. 20 CUNHA R N, SANTOS K G, LIMA R N, et al. Repose angle of monoparticles and binary mixture: an experimental and simulation study[J]. Powder Technology, 2016, 303: 203-211. 21 杜欣,曾亚武,高睿,等. 基于CT扫描的不规则外形颗粒三维离散元建模[J]. 上海交通大学学报,2011,45(5): 711-715. 22 石林榕,吴建民,孙伟,等. 基于离散单元法的水平圆盘式精量排种器排种仿真试验[J]. 农业工程学报,2014,30(8): 40-48. SHI Linrong, WU Jianmin, SUN Wei, et al. Simulation test for metering process of horizontal disc precision metering device based on discrete element method[J]. Transactions of the CSAE, 2014, 30(8): 40-48. (in Chinese) 23 ASAE S368.4- 2000. Compression test of food materials of convex shape [S].2000. 24 YAN Z, WILKINSON S K, STITT E H, et al. Discrete element modelling (DEM) input parameters: understanding their impact on model predictions using statistical analysis[J]. Computational Particle Mechanics, 2015, 2(3): 283-299. 25 牛康,苑严伟,罗敏,等. 双层种箱式马铃薯排种装置设计与试验[J]. 农业工程学报,2016,32(20): 32-39. NIU Kang, YUAN Yanwei, LUO Min, et al. Design and experiment of potato metering device with double-deck seed tank[J]. Transactions of the CSAE, 2016, 32(20): 32-39. (in Chinese) 27 王国强,郝万军,王继新. 离散单元法及其在EDEM上的实践[M]. 西安: 西北工业大学出版社,2010. 28 文愿运,刘马林,刘荣正,等. 颗粒离散单元法数值模拟与典型实验对比研究[J]. 中国粉体技术,2015(3): 1-5. 29 韩燕龙,贾富国,唐玉荣,等. 颗粒滚动摩擦系数对堆积特性的影响[J]. 物理学报,2014,63(17): 165-171. HAN Yanlong, JIA Fuguo, TANG Yurong, et al. Influence of granular coefficient of rolling friction on accumulation characteristics[J]. Acta Physica Sinica, 2014, 63(17): 165-171. (in Chinese) 30 王俊,许乃章,胥芳. 桃子冲击力学特性及其与桃子硬度的数学模型[J]. 农业机械学报,1994,25(4): 58-62. 31 ZHOU Y C, XU B H, YU A B, et al. An experimental and numerical study of the angle of repose of coarse spheres [J]. Powder Technology, 2002, 125(1): 45-54. 32 YANG J, XUAN K, BIN L I, et al. Study on release mechanism of inhibitory components from cinnamon and clove powders [J]. Journal of Food Safety, 2012, 32(2): 189-197. 33 GHODKI B M, GOSWAMI T K. DEM simulation of flow of black pepper seeds in cryogenic grinding system [J]. Journal of Food Engineering, 2017, 196: 36-51. 34 张锐,韩佃雷,吉巧丽,等. 离散元模拟中沙土参数标定方法研究[J/OL]. 农业机械学报,2017,48(3): 49-56. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170306&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2017.03.006. ZHANG Rui, HAN Dianlei, JI Qiaoli, et al. Calibration methods of sandy soil parameters in simulation of discrete element method[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 49-56. (in Chinese) 35 ZHOU Y C, WRIGHT B D, YANG R Y, et al. Rolling friction in the dynamic simulation of sandpile formation [J]. Physica A: Statistical Mechanics & Its Applications, 1999, 269(2-4): 536-553. 36 赖庆辉,马文鹏,刘素,等. 气吸圆盘式微型薯排种器充种性能模拟与试验[J/OL]. 农业机械学报,2017,48(5): 44-53. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170505&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2017.05.005. LAI Qinghui, MA Wenpeng, LIU Su, et al. Simulation and experiment on seed-filling performance of pneumatic disc seed-metering device for mini-tuber[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(5): 44-53. (in Chinese) 37 MARIGO M, STITT E H. Discrete element method (DEM) for industrial applications: comments on calibration and validation for the modelling of cylindrical pellets [J]. Kona, 2015, 32:236-252. 38 袁志发,周静芋. 试验设计与分析[M]. 北京:高等教育出版社,2000: 292-303. 39 徐中儒. 农业试验最优回归设计[M]. 哈尔滨:黑龙江科技出版社,1998: 181-187.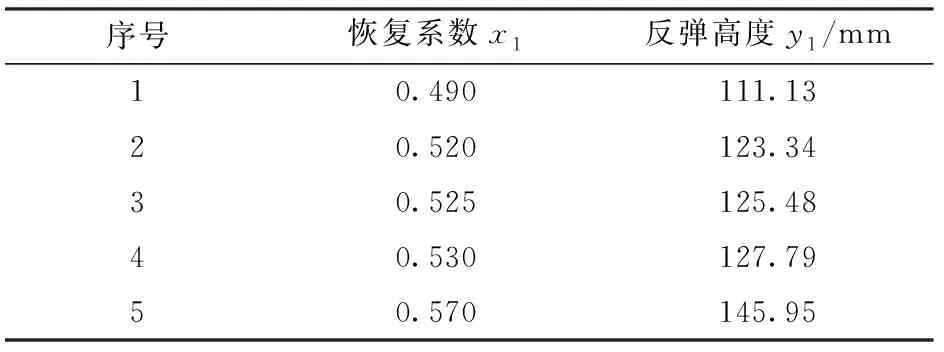

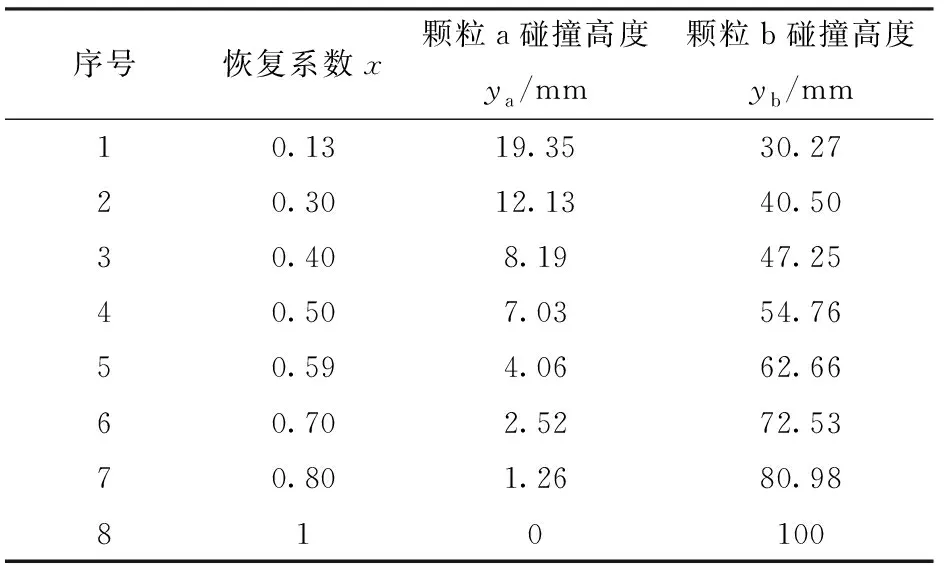
2.2 微型薯- 钢板摩擦因数
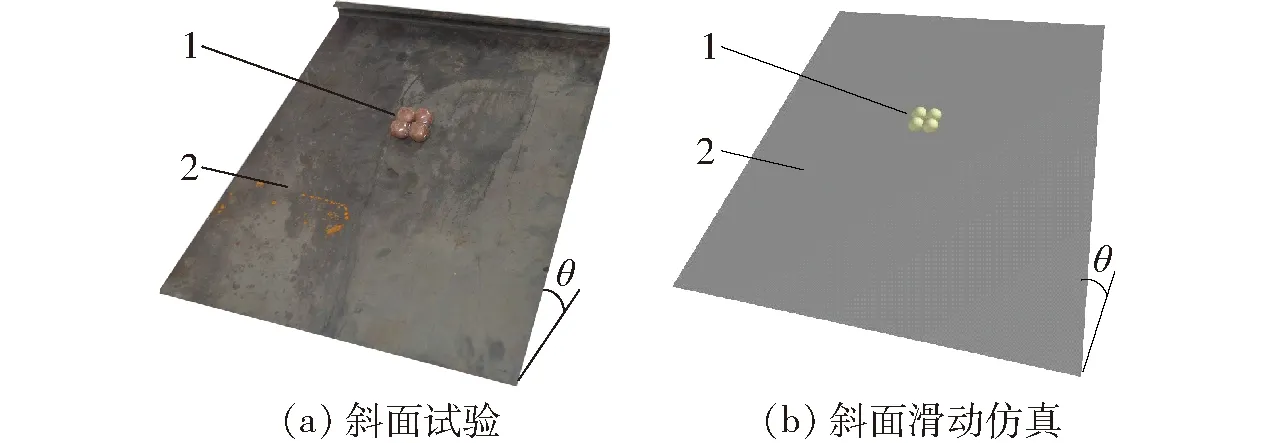
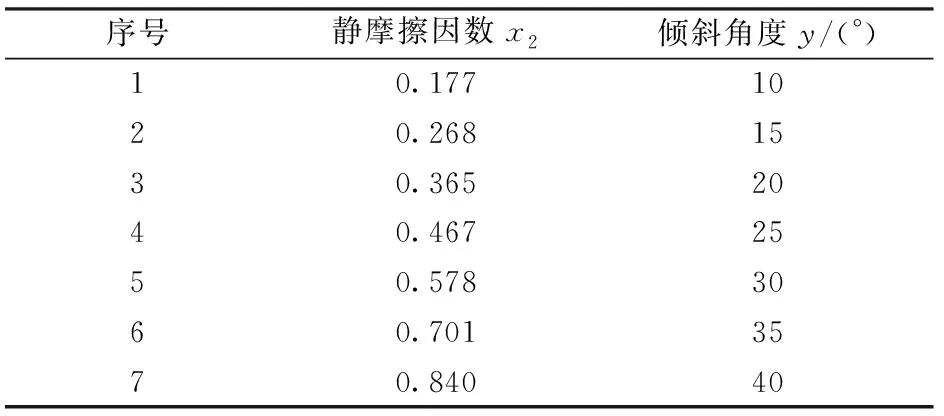


2.3 微型薯颗粒间摩擦因数
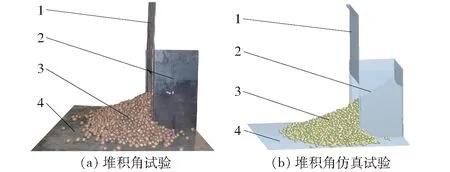
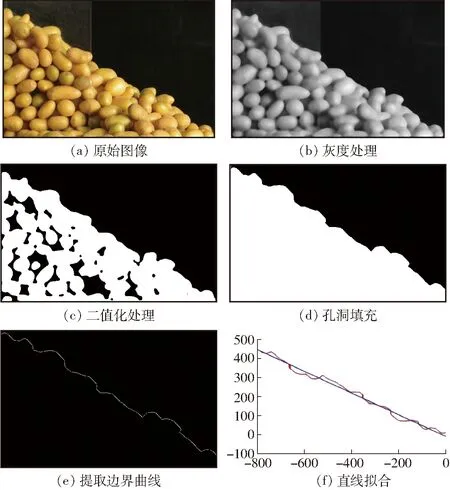





3 验证试验
3.1 圆筒提升法堆积角试验


3.2 落种试验

4 结论

