定压非稳流压水试验求水文地质参数方法

陈志强 高成城 任水源 欧宇

摘要：针对传统吕荣试验的诸多不足和限制，通过建立含水层在定压压水条件下的非稳流场数学模型，利用定压压水试验非稳流阶段的观测结果，分别采用直线法、配线法和迭代法推求出了岩体的渗透系数、压力传导系数和单位储水系数等水文地质参数。结果表明：采用不同计算方法求得的岩体渗透系数较为接近，而压力传导系数和单位储水系数对计算方法更为敏感；直线法和配线法易受到观测精度等因素的影响；迭代法适用性较强，可以有效避免人为数据选取和一些精确度较低的观测值的影响。

关键词：压水试验；非稳流；迭代法；水文地质参数

中图分类号：TV139 文献标志码：A doi：10.3969/i.issn.1000-1379.2018.01.031

在水利水电、交通、采矿以及核废料处理等工程建设中，岩体渗透系数、压力传导系数、单位储水系数等是必不可少的水文地质参数。在目前的工程勘测中，计算简便的吕荣试验使用最为广泛[1]。然而，吕荣试验所要求的稳定水流条件在实际勘测中往往难以达到[2]，而且用近似稳定流阶段的单点试验数据进行地下水流计算，不可避免地会导致较大的计算误差[3]。为保证勘测的准确性，需要较高的试验观测精度，或通过多次、多段压水试验进行参数校正[4]，此外还需要根据岩体中紊流、层流、扩张、劈裂、冲蚀和淤堵等现象采取不同的取值方法[5]，更为重要的是，吕荣试验仅能求出岩层的饱和渗透系数，不能得到全面的岩体水文地质参数[3]。

实际上，在压水试验中，非稳流是一种常见状态，尤其在试验初期，岩体中的流场随时间的变化十分显著，流场的变化过程是岩体水文地质参数的反映。因此，本文尝试采用定压压水试验中的非稳流测量数据推求岩体的水文地质参数。

1 模型与计算方法

1.1 定压三维非稳流压水试验数学模型

在压水试验中，试段往往不能贯穿整个潜水含水层，理论上应将该试段作为不完整注水井，但不完整井数学模型参数推求需要信息较多，而且大多数情况下难以将整个含水层进行均质化处理以满足非完整井的求解条件[2]。事实上，当含水层厚度较大时或试段长度相对于含水层厚度较小时，注水试段在整个含（导）水层中可以看作一个点源，非稳流压水试验水流场可以概化为三维球形扩散流，该非稳流压水试验的水流场方程及定解条件为

在进行求解时，先设定各参数一组初值，然后代入水流场模型进行迭代计算，直至两次求解得到的参数值的差异小于设定的誤差阈值，即满足式（13）时，便认为得到的参数是所要求的水文地质参数。由于这种方法难以通过人工计算进行求解，因此采用VB6.0语言开发的程序进行计算。

2 计算实例

2.1 定压压水试验

压水试验在贵阳鹿角坝地区进行，该地区属典型的喀斯特峰丛洼地地貌。以往勘测资料表明，该地区潜水位约为1285m，其中1235m高程以下岩层的透水率在3Lu以下，可以作为隔水层处理，潜水含水层的总厚度约为34.3m。

压水试验的各试段参数见表1，各试段高程分布在潜水面至其下19.3m范围内。各试段长度相对于潜水层总厚度较小，因此各压水试段可以看作点源。在两个主裂隙发育方向设置观测孔进行观测，观测孔直径为91mm，距离注水井2～3m。在试验过程中，采用BL-YW500液位计自动测量并记录注水井水位，将流量表和三角堰结合起来测量压水开始后第2、4、6、8、10、12min的观测孔流量。

2.2 结果与分析

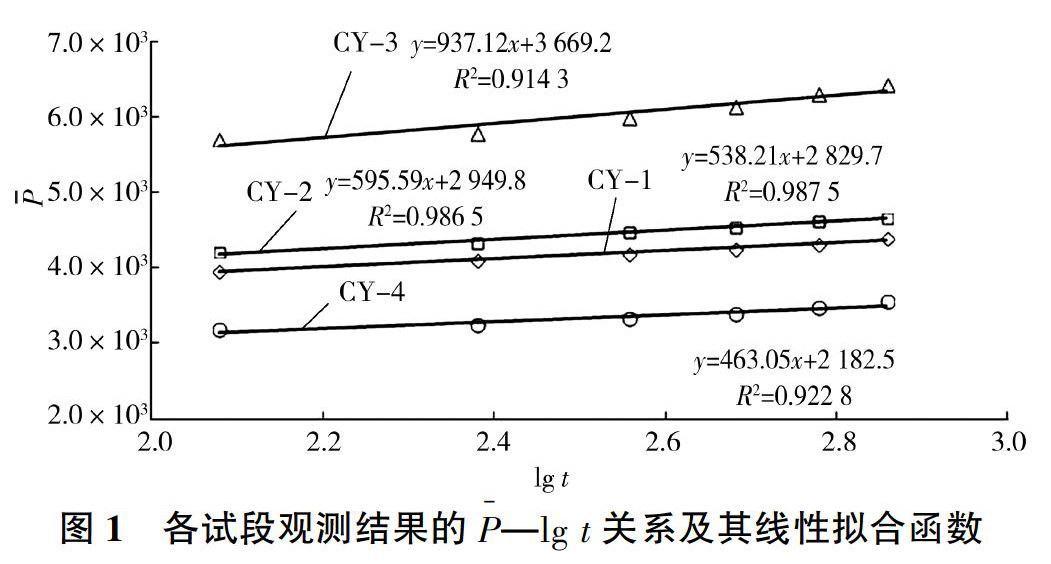
依据各试段压水试验观测结果得到的P-lgt关系（见图1），线性拟合结果表明，各试段得到的尸一lgt线性复相关系数R2均在0.9以上，即具有显著线性相关关系。根据各线性拟合函数及测量得到的含水层厚度，采用式（8）可推求岩体水文地质参数。

在采用配线法进行参数推求时，首先在各试段压水试验的观测结果中分别选取一组Q1、Q2值，采用式（9）计算相应的β值，然后在β-lga线中查出相应的压力传导系数a，得到各试段的β和a值，见表2。根据表2及其他观测结果，采用式（10）和式（11）可以求出岩体的渗透系数和单位储水系数等水文地质参数。

迭代法求得的各试段流量观测值与计算值见图2，可以看出，当迭代计算结束时，观测孔处的流量计算结果与实测结果十分接近，除个别值外，计算结果的相对误差均在3%以下，而均方根误差均在0.8L/min以下，显示出较好的计算精度，此时模型采用的计算参数即为各试段水文地质参数。

采用直线法、配线法和迭代法推求的各试段水文地质参数值见表3。可以看出，不同计算方法得到的水文地质参数的值并不相同，通过比较可以发现，各方法计算得到的岩体渗透系数较为接近，压力传导系数和单位储水系数的计算结果则存在显著差别。说明这3种方法计算岩体渗透系数均较为可行，但压力传导系数和单位储水系数对计算方法更为敏感，因此在计算方法的选取上要更为慎重。

采用直线法和配线法时需要同时用到注水井处的地下水水位和观测井处的流量观测值。由于压水试验的持续时间仅12min，注水井处的地下水水位往往在观测初期发生显著变化，其上升幅度达到2.5～3.5m，在其后的观测过程中不再发生显著变化，例如在2-12min变化幅度仅5～10cm，因此若非采用十分精确的观测手段，则难以准确得到地下水水位变动过程，从而导致计算结果出现较大误差。由于在配线法中仅采用一组流量观测结果进行试算，因此观测数据的选取对计算结果有显著影响。

相对而言，尽管迭代法的计算过程较为繁琐，但是通过编程求解也能较为方便地得到各水文地质参数的计算值，而且由于迭代计算的假设条件少，理论基础更为严格，因此其适用性更强。更为重要的是，迭代法是综合所有试验观测数据得到的最优参数计算结果，避免了人为选取数据导致的误差，而且这种方法并不依赖特定的观测结果，在试算过程中可以仅采用精确度更高的观测结果（如流量）与计算结果进行比较，避免了一些观测精度不太高的观测值对计算结果的干扰。

3 结语

直线法、配线法、迭代法求得的岩体渗透系数较为接近，压力传导系数和单位储水系数对计算方法更为敏感；迭代法相较而言适用性较强，可以有效避免人为数据选取和一些精确度较低的观测值的影响。

参考文献：

[1]张承志.钻孔压水吕荣试验及应用[J].西北水电，1994（2）：21-24.

[2]张祯武，李兴成，徐光祥.利用定压力非稳定流压水试验求水文地质参数[J].岩石力学与工程学报，2004，23（15）：2543-2546.

[3]张祯武，陈官权，徐光祥.利用吕荣试验资料计算水文地质参数的新法压水试验方法[J].工程勘察.2003（4）：19-22.

[4]戴亮，杨霞.吕荣式压水试验方法在勘测中的应用[J].东北水利水电，1992，10（9）：35-38.

[5]叶世雄，王红喜，钟灵.中美规范中吕荣值的异同及几点建议[J].江西煤炭科技，2007（4）：96-97.

[6]中华人民共和国水利部.水利水电工程钻孔压水试验规程：SL 31-2003[S].北京：中国水利水电出版社，2003；25-26.