旋流式竖井涡室水边线的计算方法

赵建永 刘韩生 徐自立 于敬舟

摘要：旋流式竖井，涡室水边线问题一直是研究的重点问题。目前，旋流式竖井涡室水边线的计算并没有明确的理论计算方法，主要依赖水工模型试验测量得到的试验数据。通过Ippen冲击波理论和刘韩生缓冲击波简化式分别计算了涡室水边线，对比栗西沟旋流式竖井试验数据，得知后者计算精度更高，计算过程更加简单，可满足工程的需要。

关键词：旋流式竖井；涡室；水边线；计算方法；冲击波；简化式

中图分类号：TV131.61 文献标志码：A doi：10.3969/i.issn.1000-1379.2018.01.020

旋流式竖井是一种非常优秀的泄水道，自20世纪40年代意大利人Drioli首次提出旋流式竖井开始，其受到了广泛的关注，研究成果颇多[1-5]。但是，对于旋流式竖井涡室水边线的计算暂没有明确的方法，而水边线作为水力学研究的重点之一，在旋流式竖井涡室边墙高度选择上起着非常重要的作用，准确的水边线计算有助于选取最合适的涡室侧墙高度，从而节约工程投资。

冲击波是明渠水流的常见现象，20世纪40年代Ippen A.T.等[6-7]提出冲击波基本理论，得到陡冲击波计算公式。该理论目前被各教科书普遍公认，但是，该公式形式复杂，在计算中需要进行反复的迭代计算，用诺模图法求解时，人为因素会对计算精度产生影响，实际工程中不便使用。20世纪90年代，刘韩生等[8]在Ippen冲击波理论基础上，利用比能不变假定得出计算误差基本相同的缓冲击波简化式，计算简单，应用方便。刘韩生缓冲击波简化式在窄缝挑坎以及收缩渠道等方面得到了广泛的应用[9-14]，展现了其在水边线计算方面的潜力，使得其拥有了计算旋流式竖井涡室水边线的可能。本文在栗西沟旋流式竖井水工模型试验的基础上，通过Ippen冲击波理论和刘韩生缓冲击波简化式对涡室水边线进行了比较精确的计算。

1 应用刘韩生缓冲击波简化式对水边线的计算

刘韩生等根据Karmam冲击波积分式，利用比能不变假定推导的缓冲击波简化式如下：式中：h1、h2分别为涡室边墙前、后点水深；α为前后两点的偏转角度；Fr1、Fr2分别为涡室边墙前、后点的弗劳德数。

由文献[8]可知，式（1）形式简单，其忽略了高阶小量，虽然造成波角的计算与未简化前相比有一定的误差，但是误差不大，相对来说，計算精度较高，可满足实际工程的需要。

水流自引水道进入涡室，引水道水深较浅，水流比较平稳，进入涡室后水流顺时针旋转，水流壅高，形成具有稳定的、与大气连通的空腔旋转流运动。在工程设计中，涡室进口前的水流参数偏转角度α、弗劳德数Fr1、水深h1已知，需要确定偏转角度α后的水深h2。如图1所示，旋流式竖井椭圆曲线涡室体形的涡室部分由1/4椭圆曲线与圆弧组成，构成涡室的曲线边墙。在涡室的曲线边墙部分发生冲击波，水流壅高，从涡室进口处A点开始进行涡室水边线的计算，在偏转角度α（即椭圆弧AB的角度为α）后，冲击波到达B点，则由进口处A点的弗劳德数Fr1以及水深h1可以计算出B点的水深h2（在椭圆曲线边墙部分水深即为水面至涡室底板，而由于圆弧部分边墙不存在底板，直接与渐变段连通，因此这里将水深暂定为水面至二者相接处的高度）。这样依次计算出涡室边墙各处的水深hi，便可以计算旋流式竖井涡室的水边线，得到完整的一条水边线。由任一点i发出的波前与轴线y=D/2的交点坐标xki。比较每一个xki，其中最小的即为冲击波在轴线处交汇点的横坐标。在求出βi+∑αi-1后，利用作图法亦可方便求出xki。

把式（3）～式（5）应用于每一微小段的侧墙转折，可转化为式中：hi-1、hi分别为涡室边墙第i-1、i点水深；αi、βi分别为第i点的侧墙偏转角、波前方向角；Fri-1、Fri分别为涡室边墙第i-1、i点的弗劳德数。

根据式（8）～式（10），用前述方法即可算出冲击波交汇点的位置。每一步求出的hi可作为i点与i+1点连线中点处靠侧墙的水深，连接各个hi，即可得到涡室侧墙的一条完整水面线。

3 实际水工模型的计算实例

栗西沟尾矿库旋流式竖井水工模型试验所用模型按重力和阻力相似准则设计，几何比尺λL=20，用有机玻璃制作。试验的最大流量为22m3/s，分别选取大、中、小三个典型流量22、15、8m3/s进行研究，测量涡室边墙水边线，流量22m3/s下涡室的水边线测点展开图如图3所示。

通过刘韩生缓冲击波简化式和Ippen冲击波理论两种方法，可以将旋流式竖井涡室水边线的各处水深计算出来，如图4～图6所示（Liu值为刘韩生缓冲击波简化式计算结果）。两种方法都可以近似用来分析涡室的水边线问题，二者的计算结果均比试验值略大，但是前者的计算值相对偏差要比后者的小得多，即前者的计算精度要高得多。

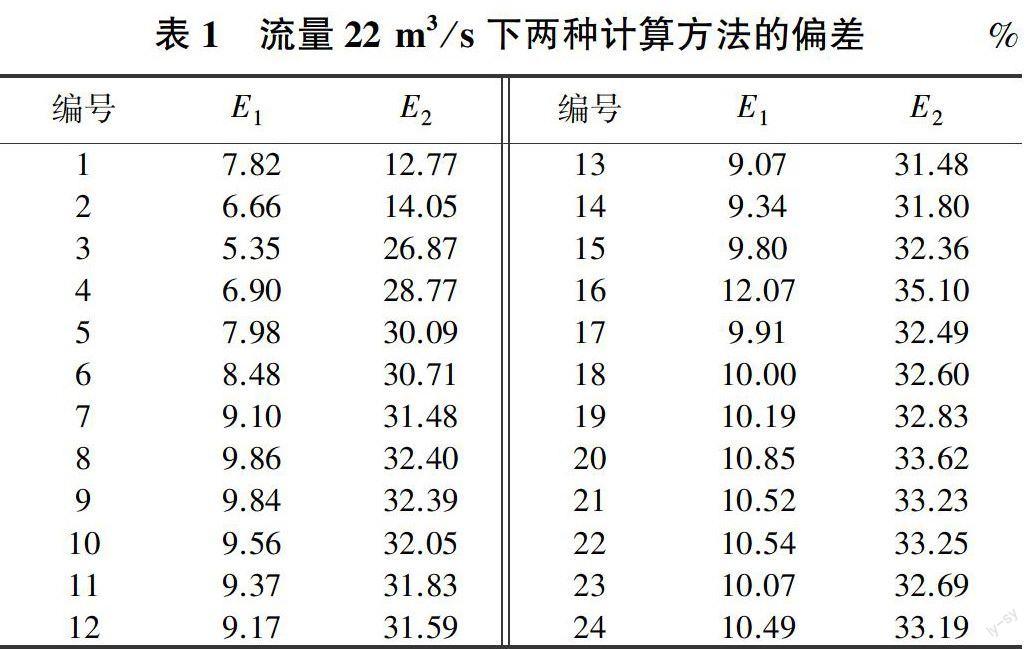
为了更加精确地对两种方法计算结果进行对比，下两种计算方法的偏差见表1。

由表1可知：当流量为22m3/s时，Ippen冲击波理论的平均计算偏差为30.28%，而刘韩生缓冲击波简化式的平均计算偏差仅为9.67%。另外，当流量分别为15、8m3/s时，两种方法的平均计算偏差分别为15.07%、13.73%以及9.16%、8.41%。计算结果表明，刘韩生缓冲击波简化式的计算精度高于Ippen冲击波理论的，更能满足实际工程的需要。

4 结论

栗西沟工程实例计算结果表明，在旋流式竖井涡室水边线计算方面，刘韩生缓冲击波简化式相对Ippen冲击波理论计算精度更高，计算过程更加简单快捷，不需要繁琐的迭代试算过程，更满足实际工程的需要。

参考文献：

[1]VISCHER D L，HAGER W H.Vortex Drops，Energy Dissi-paters[J].Hydraulic Structure Design Manual，1995（9）：234-238.

[2]HAGER W H.Vortex Drop Inlet for Supercritical ApproachingFlow[J] .Journal of Hydraulic Engineering，1990，116（8）：1048-1054.

[3]董兴林，高季章.超临界流旋涡竖井式溢洪道设计研究[J].水力发电学报，1996，15（1）44-48.

[4]董兴林，余闽敏，吴曾谋，等.导流洞改建旋流式竖井泄洪洞研究与应用[J].水力发电学报，2002，21（4）27-29.

[5]倪漢根，周晶，周迎新.坝身竖井旋流泄洪消能的设想[J].大连理工大学学报，1999，39（2）：318-325.

[6]IPPEN A T.Gas-Wave Analogies in Open Channel Flow[C]// Proceedings of 2nd Hydraulics Conference.Iowa：U-niversity of Iowa，1943：248-265.

[7]斯里斯际C M.高水头水工建筑物的水力计算[M].毛世民，杨立信，译.北京：水利电力出版社，1984：113-135.

[8]刘韩生，倪汉根.急流冲击波简化式[J].水利学报，1999，30（6）：56-60.

[9]刘韩生，倪汉根，梁川.对称曲线边墙窄缝挑坎的体型设计方法[J].水利学报，2000，31（5）：70-75.

[10]刘韩生，倪汉根，梁川.非对称窄缝挑坎的边墙曲线计算方法[J].水力发电学报，2001，20（3）：59-67.

[11]倪汉根，刘韩生，梁川.兼使水流转向的非对称窄缝挑坎[J].水利学报，2001，32（8）：85-89.

[12]樊有锋，刘韩生，姬春利.对称直线收缩段急流冲击波的水力计算[J].中国农村水利水电，2009（10）：121-124.

[13]樊有锋，刘韩生，姬春利.对称直线收缩渠道段长度的计算方法[J].中国农村水利水电，2009（12）：108-110.

[14]樊有锋，刘韩生，姬春利.缓冲击波简化理论在收缩渠道中的应用研究[J].人民长江，2009，40（20）：13-15.

[15]高季章.窄缝式消能工的消能特性和体型研究[G]//中国水利水电科学研究院科学研究论文集.北京：水利电力出版社，1983；213-236.