基于不同接触单元的面板堆石坝动力响应分析

程玲 董景刚

摘要：土工结构数值模拟中土与结构接触问题一直是学者研究的热点。通过改变普通四边形单元等效线性黏弹性动力本构模型中的动剪模量和模量指数，提出一种改进薄层接触单元，其与普通四边形单元本构模型一致，物理意義更为明确，模型计算参数更易取得，更适于土与结构接触面的计算。对坝高为200m的面板堆石坝面板与垫层之间设置改进的薄层接触单元、不加接触单元、采用无厚度的Goodman单元及改变薄层接触单元动力参数等多种工况时，面板的动力响应结果分析比较表明：面板与垫层之间设置改进的薄层接触单元时面板的动力响应介于不设接触单元和设无厚度的Goodman单元之间，合理选取薄层接触单元动力参数可以得到理想的结果。

关键词：Goodman单元；改进薄层单元；动力响应；接触面；面板堆石坝

中图分类号：TV641.4+3 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.01.018

水电工程中土与刚性结构之间不存在真实的过渡体，由于两种接触材料物理力学性质差异巨大，外部荷载作用往往会使接触面两侧结构产生较大的变形差异，并且数值模拟时在接触面处往往会产生比实际更大的剪应力，导致计算结果不尽合理，因此数值模拟时在两种结构接触面上需设置特殊的接触单元进行过渡，以得到更准确合理的计算结果[1]。目前常采用无厚度Goodman单元和薄层接触单元等特殊单元来模拟接触面之间的相互嵌入、脱离、相对位移等。常用的接触单元本构关系都是基于各种假设建立的，因此接触单元类型及参数的选取和应用对于数值计算结果的准确性极为重要。本文以200m高面板堆石坝为例，分别在面板与垫层之间不设任何接触单元、设置无厚度的Goodman单元、设置改进薄层接触单元来模拟两者之间的接触，计算不同工况下面板坝的动力响应，并对计算结果及薄层接触单元参数敏感性进行探讨。

1 常用接触单元简介

1.1 无厚度Goodman单元

该单元为无厚度一维单元，由4节点组成。由于其物理意义较为明确且无厚度，可以较好地反映材料性质差异较大的两种结构接触面上的张裂和相对滑动，因此得到了广泛应用。然而，只有当两种材料之间的接触面较为光滑时，剪切破坏才发生在这两种材料的接触面上。对于绝大多数相对粗糙的两种材料接触时，破坏面一般发生在土体内部，此时用无厚度的Goodman单元进行数值模拟存在一定的缺陷。鉴于此，李守德等[2]对Goodman单元进行了修正，使其有限元实现更为灵活。

1.2 Desai薄层单元

Desai薄层接触单元[3-5]可以解决无厚度单元在受压时接触面两侧相互嵌人及接触面粗糙时破坏面发生在土体内部的情况，并且能更好地模拟接触面的受力变形，所以被广大学者所接受。其本构关系为式中；t为单元厚度；σn为法向应力；τs为切向剪应力；knn为法向劲度系数；kss为切向劲度系数；εn为法向应变；εs为切向应变。

值得注意的是，Desai等在研究中[3-5]只指出t=（0.01～0.10）B（B为单元的长度），并没有给出t的具体值，所以其取值有一定的随意性。

1.3 改进的薄层单元

张冬霁等[6]通过一系列接触面单剪试验，较为深人地分析了接触面的破坏机理，建立了一种接触面本构模型，并将其用于接触面的有限元计算中，取得了较满意的结果。

殷宗泽等[7]对Desai薄层单元进行改进，改进后的薄层接触单元与普通单元的本构假设、应变场定义模式相统一，并没有引入其他参数，只是将土体自身的变形分为土体的基本变形和破坏变形两部分，其概念更为明确，因此具有更高的应用价值。

2 模型及计算参数选取

2.1 计算模型

图1为面板堆石坝计算模型。坝顶宽15m，上、下游坝坡坡比均为1：1.4，面板顶部厚度为0.3m、底部厚度按《混凝土面板堆石坝设计规范》（SL228-2013）[8]中的公式计算后取0.9m。计算模型网格尺寸取坝高的1/20，在混凝土面板与堆石之间依次设置5.0m厚的垫层和5.0m厚过渡层，均上下等宽。计算坝高为140m，面板在坝高为100m处设水平施工缝。

2.2 单元本构模型及计算参数

（1）面板混凝土强度取C30，重度取25.0kN/m3，泊松比取0.165，弹性模量取35GPa，动力本构模型采用线弹性模型。

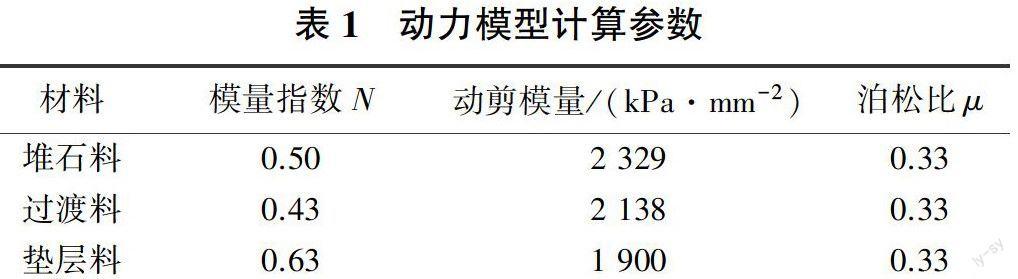
（2）坝体垫层料、过渡料、堆石料采用等效线性黏弹性动力本构模型[9]，坝体垫层料、过渡料、堆石料计算参数见表1。

（3） Goodman单元的动力本构模型采用河海大学的试验结果[10-13]，计算参数见表2。

接触面的最大动剪模量可表示为式中：σn为法向应力。

接触面单元的动剪模量K与动剪应变γ的关系为式中：τf为破坏剪应力，τf=σntanφ，其中φ为接触面摩擦角。

接触面单元的阻尼比λ计算公式为式中：λmax为最大阻尼比，取0.2。

（4）通过改变普通四边形单元等效线性黏弹性动力本构模型中的动剪模量K和模量指数N，提出一种特殊接触单元。改进薄层单元的动剪模量K和模量指数N取值见表3，泊松比μ见表1。

2.3 计算地震波

动力计算时地震波选用2008年汶川大地震中茂县地震波，水平向峰值地震加速度取0.39，竖向峰值地震加速度取0.2g。动力响应分析时分别在面板与垫层之间设置无厚度Goodman单元、不设置任何接触单元、厚度为10cm（计算模型网格尺寸的1/100）的改进薄层单元.具体计算工况见表3。

3 结果分析

面板与垫层之间设置不同接触单元，薄层单元动剪模量K分别取不设接触单元时的动剪模量（即K=1 900kPa/mm2）的0.50倍、0.33倍、0.25倍、0.20倍，模量指数N改变时顺河向最大加速度放大倍数和竖向最大加速度放大倍数见表4。

从表4可以看出，顺河向最大加速度放大倍数小于竖向放大倍数，设置接触面单元工况的最大加速度放大倍数小于不设置接触单元的，说明若面板与垫层之间不设接触单元，面板與垫层材料刚度的差异就会导致计算刚度矩阵分布不合理，从而产生较大的变形和动力反应误差。

动剪模量K对加速度放大倍数的影响要大于模量指数N的；随着改进的薄层单元动力本构模型中参数K和N取值的减小，相应的加速度放大倍数也减小。说明随着动剪模量K和模量指数N取值的减小使面板与垫层之间的材料差异得到了较好的过渡，面板上一定的剪力转移到了垫层上，从而使得面板与垫层之间实现更好的变形协调。

图2为面板与垫层之间不设接触单元、设置无厚度Goodman单元、设置改进的薄层单元（N=0.50，动剪模量取0.50K）时面板顺河向和竖向加速度放大倍数沿坝高的分布情况。

由图2可以看出，加速度放大倍数随着坝高的增高呈现先缓慢减小后迅速增大的趋势，在约0.8坝高处突然大幅增大（鞭梢效应），所以在实际工程设计施工时相对坝高超过0.8时要采取一定的抗震加固措施。

4 结语

在进行土与结构数值模拟时采用接触单元是十分必要的。本文通过改变普通四边形单元计算参数得到一种特殊的薄层接触单元，其与普通四边形单元本构模型一致，物理意义更为明确，模型计算参数更易取得，更适于土与结构接触面的计算。对坝高为200m的面板堆石坝动力响应分析表明：面板与垫层之间不采用接触单元时面板动力响应最大，采用无厚度的Goodman单元时面板动力响应最小，改变薄层单元的动力参数对动力响应有一定的影响，当模量指数N取0.4、动剪模量取垫层料动剪模量的0.2倍时，面板动力响应与采用Goodman单元很接近；合理选取改进薄层接触单元的计算参数，可以很好地模拟面板与垫层之间的过渡。

参考文献：

[1]朱泓，殷宗泽.土与结构材料接触面性能研究综述[J].河海科技进展，1994（4）：1-8.

[2]李守德，俞洪良.Goodman接触面单元的修正与探讨[J].岩石力学与工程学报，2004，25（4）：2628-2631.

[3]DESAI C S，MA Y.Modelling of Joints and Interfaces Usingthe Disturbed-State Concept[J].International Journal for Nu-merical and Analytical Methods in Geomechanics，1992，16（9）：623-653.

[4]DESAI C S，RIGBY D B.Cyclic Interface and Joint ShearDevice Including Pore Pressure Effects[J].Journal ofGeotechnical and Geoenvironmental Engineering，1997，123（6）：568-579.

[5]DESAI C S，PRADHAN S K，COHEN D.Cyclic Testingand Constitutive Modeling of Saturated Sand-Concrete Inter-faces Using the Disturbed State Concept[J].InternationalJournal of Geomechanics，2005，5（4）：286-294.

[6]张冬霁，卢廷浩一种土与结构接触面模型的建立及应用[J].岩土工程学报，1998，20（6）：62-66.

[7]殷宗泽，朱泓，许国华.土与结构材料接触面的变形及其数学模拟[J].岩土工程学报，1994，16（2）：14-22.

[8]中华人民共和国水利部.混凝土面板堆石坝设计规范：SL 228-2013[S].北京：中国水利水电出版社，2013：16-17.

[9]韩国城，孔宪京，李俊杰.面板堆石坝动力破坏性态及抗震措施试验研究[J].水利学报，1990，21（5）：61-67.

[10]丁勇春，王建华，陈锦剑.接触面单元计算方法探讨[J].岩土力学，2006（S1）：211-213.

[11]胡黎明，濮家骝.土与结构物接触面物理力学特性试验研究[J].岩土工程学报，2001，23（4）：431-435.

[12]胡黎明.土与结构物接触面数值模拟[J].工程力学，2001（增刊）：467-471.

[13]栾茂田，武亚军.土与结构间接触面的非线性弹性-理想塑性模型及其应用[J].岩石力学，2004，25（4）：507-513.