动态环境下无线Mesh网络骨干节点部署算法
曹圣灵,李枚毅,胡 灿
(湘潭大学 信息工程学院,湖南 湘潭 411105)
0 概述
无线Mesh网络(Wireless Mesh Network,WMN)[1]是一种多跳无线网络,是与传统无线网络不同的一种无线网络。相比传统无线网络,它具有部署简单、稳定系强、带宽高、可扩展性强、应用广泛、发展前景好等优点。在无线网络日益发达的时代,无线Mesh网络已经获得了国内外大量研究者的关注。Mesh路由器(Mesh Router,MR)、Mesh网关(Mesh Gateway,GW)和Mesh终端(Mesh Client,MC)是组成无线Mesh网络的基础框架。MR在网络中具备接入和转发功能,为其覆盖范围内的MC提供网络服务,在多跳网络中为其他MR转发数据到MG。MG是特殊MR,不仅具有MR在网络中的功能,还以有线形式与因特网(Internet)连接,承担与Internet的连接任务。MC是通过MR访问网络的终端设备,如笔记本电脑、手机等。
文献[2]提出贪心算法NF-Greedy,该算法迭代从可部署MR集合中获取权重最大的节点添加至部署节点集合,建立部署在MR数量最小化的目标上,利用网络流方法进行求解。文献[3]将WMN网络MG布置问题抽象为几何上的K-中心问题,以最小化MR和MG之间路径长度为目标,提出自适应的粒子群优化算法来求解网关节点部署问题。文献[4]针对WMN骨干网络部署优化问题,以满足用户带宽需求和网络连接为前提,以最小化MR数量为目标,提出在MG与MR互相影响情况下的解决方法。
目前在静态环境下WMN骨干网络节点部署问题寻找最优方案已经比较成熟[5-10],但WMN往往处于动态环境下,MR与MC具有可变性,所以动态环境下的研究更加有意义。当前已经有部分国内外的学者针对动态环境下的部署问题提出了研究。文献[11]提出一种粒子群优化算法,该算法在动态环境下,以最大化满足网络连接和覆盖需求为前提,实现MR的部署方案。但是该文献假定MR的部署位置是可以任意移动的,这在现实生活中实现成本太高。本文研究MG与MR组成的WMN骨干网络,提出一种动态环境下WMN骨干网络节点的优化部署算法。
1 问题描述
现实生活中WMN是动态变化的,在不同的时间段MC会处于不同的需求状态和地理位置。用户发生需求变化后在接下来的一段时间是维持稳定,因此,本文假定检测到需求变化后,调整骨干节点的部署位置适应需求变化,度过周期后再检测新环境。在一个恰当的部署候选位置,且已将用户的需求离散化为需求点的二维平面场景中,骨干节点部署问题将被看作是二维平面节点部署问题。
1.1 定义及变量说明
在研究该问题时,本文假定无线网络通信可靠,且节点之间通信互不干扰,设定如下变量:
Rc(节点覆盖半径),指以MR为中心向MC提供服务区域的半径。
Rt(节点通信半径),指以MR为中心能够与其他MR通信区域的半径。
Cap(最大接入容量),指MR提供给MC带宽的最大值。
H(最大跳数),指确保通信质量的前提下,MR至MG通信路径允许跳数的最大值。
T(周期值),指根据现实情况,假定网络中用户需求趋于稳定的时间段值。
在二维平面内,WMN对应着一个拓扑图G=(V,E),集合V={v1,v2,…,vn}表示网络中节点集合;邻接矩阵E={ei,j|i,j∈{1,2,…,n}}表示节点之间的关系,当节点vi和vj之间的通信距离未超过节点的通信半径,即dist(vi,vj)≤Rt时ei,j=1,否则ei,j=0。根据上文所提出的假设,为方便本文的说明,作出如下定义:
定义1(MR候选位置(MR Candidate,MRC)) 指事先在场景中选取能够布置MR的位置,用集合C={c1,c2,…,cn}表示,其中MG数量为L。
定义2(用户需求点(User Demand Node,UDN)) 指场景内用户的带宽需求分布被离散化后形成的点,用集合U={u1,u2,…,um}表示。
定义3(实际覆盖半径) 指骨干节点为其覆盖的UDN实际上能够提供服务的最大距离。
定义4(相邻候选位置) 指可供部署的MRC,该MRC与骨干网络之间没有未提供服务的UDN且与骨干网络的距离为1。
定义5(环境改变次数) 指当前运行的时间度过了几个周期值T,即环境改变的次数t。
为更好地量化模型,补充如下变量:
集合B={b1,t,b2,t,…,bm,t}表示当前UDN集合中点的带宽需求值,bj,t表示UDN集合中uj在当前环境的带宽需求值。
集合Dct={di,j|i∈{1,2,…,n}∧j∈{1,2,…,m}}表示MRC对流量需求的覆盖关系,当dist(ci,uj)>Rc时di,j=0,表示用户需求点uj不在ci覆盖范围内;当dist(ci,uj)≤Rc时di,j=1,表示用户需求点在覆盖范围内。
集合G={g1,t,g2,t,…,gn,t}表示在当前环境下MRC是否被选为部署网关,gi,t=0表示ci在当前环境未被选作网关,gi,t=1表示ci被选作网关。
集合X={x1,t,x2,t,…,xn,t}表示当前环境下MRC集合中位置是否部署了骨干节点,xi,t=0表示ci位置未部署节点,xi,t=1表示ci位置部署了节点。
集合Y={yi,j|i∈{1,2,…,n}∧j∈{1,2,…,m}}表示骨干节点vi所承担用户需求点uj的带宽需求情况。
集合R={r1,t,r2,t,…,rn,t}表示当前运行次数骨干节点剩余可分配的带宽值,值初始化为Cap。
集合H={h1,t,h2,t,…,hn,t}表示当前骨干节点到MG的最小跳数。

1.2 数学模型
基于上文对定义和变量的说明,本文给出问题的形式化描述,优化目标如下:
(1)
每次环境变化后,需要满足用户带宽需求,保证网络连通性,在此前提下将MR部署数量最小化。
约束条件:

(2)

(3)
di,j=1,∀yi,j≠0,∀i∈{1,2,…,n},∀j∈{1,2,…,m}
(4)
xi,t=1,∀yi,j≠0,∀i∈{1,2,…,n},∀j∈{1,2,…,m}
(5)
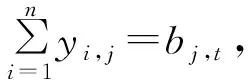
(6)
ri,t≥0,∀i∈{1,2,…,n}
(7)
hi,t≤H,∀i∈{1,2,…,n}∧xi,t=1
(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)
式(2)表明被选择MRC必须能够通过多跳网络连接到网关。式(3)表明被选择的MRC覆盖区域中必须存在可以通信的UDN。式(4)、式(5)表明当且仅当UDN在MRC覆盖范围内且MRC已经部署MR时,MRC为UDN提供网络服务。式(6)表明必须满足全网络中所有用户需求。式(7)表明骨干节点的最大接入容量不能小于其提供的带宽之和。式(8)表明最大跳数不能小于骨干节点通过多跳网络连接到MG的最小跳数。式(9)~式(11)表明仅当2个MRC都被选择部署MR,且两者能互相通信,该路径才能连接到MG。式(12)~式(15)表明节点必须满足当前条件才能存在多跳路径连接到MG。
2 WMN骨干节点部署问题算法
2.1 骨干节点部署算法
骨干节点的部署思路是,首先确定MG位置,然后迭代从未部署MRC集合中,优先选择可覆盖流量最大、实际覆盖半径最小的节点,添加至骨干节点集合,直至网络中用户需求得到满足。对于有向图而言邻接表有所缺陷,基于存取数据模型的高效性,本文采用十字链表存储数据,同时提升代码的可读性,算法步骤如下:
1)初始化场景布置变量,凭借用户需求点和MR候选位置构建需求覆盖表。
2)更新已部署MR集合、已覆盖UDN集合和需求关联表,得到当前网最多可以提供的带宽,计算目前网络中的流量,判断它是否达到预期总流量,如等于则转步骤5)。
3)更新所有节点的剩余带宽、已部署节点的最小跳数、骨干层节点的最短路径与节点可覆盖需求表,依照上文方法添加节点至骨干网络,更新剩余MRC集合。
4)从相邻候选位置中选取权重最大的位置,添加至已部署MR集合,若不存在则选取权重最大的路径,转步骤2)。
5)记录结果,算法结束。
上述的MR部署方法需要先确定MG位置,但是MG与MR位置的选择是彼此制约的。本文采用BPSO算法来部署MG,该算法初始化一个由PopSize个粒子组成的粒子群,在D维二进制空间中搜索极值,粒子群依靠历史最优解和全局最优解不断改正探寻位置,以此得到最优解。其中,粒子群速度和位置的更新公式为:
(16)
(17)
(18)
(19)
算法步骤如下:
1)生成规模为PopSize的粒子群,初始化粒子。
2)依照上文的算法布置MR,凭借式(19)得到粒子群适应度值,更新历史最佳位置和全局最佳位置。
3)根据式(16)更新粒子的速度和位置。
4)检测算法是否运行到最大迭代次数,或检测结果是否满足预期,如不满足则转步骤2)。
5)记录输出值(骨干节点数量及相应坐标)。
2.2 动态环境下的TSDPSO算法
为在动态环境中求解该算法,本文借鉴文献[12]提出的对称位移映射的双子种群PSO算法,检测当前部署方案是否能够满足网络连通性及用户需求。在D维度空间中,pbest是粒子当前最优解,gbest是种群中粒子所经历过的最优解,xi是粒子自身的位置向量,vi是粒子自身的速度向量。在算法开始时,种群等分为主、辅2个子群,主子群选择标准PSO算法的速度、位置进化方程式(20)、式(21)对粒子更新[13-14]。辅子群选择差异进化,依照方程式(21)、式(22)对粒子更新[15]。
(20)
(21)
(22)

(23)
在D种群的进化过程中,辅子群粒子采用差异进化策略,以50%的几率与全局最优粒子实施吸引或排斥,主子群粒子则始终被全局最优粒子所吸引。环境发生变化后,对现有的部署方案进行评估,判断部署方案能否满足网络连通性,计算MR是否能够满足用户带宽需求量,如不能满足目标,在原始种群基础上,对称性调整主子群粒子的空间位置分布,重新设置部署方案。空间对称位移映射步骤如下:
1)在所有维度上计算主群粒子的位置与局部最优gbest位置的差。
2)统计每一维度上位置差值的正负值数量,正值数量记为n1d(d=1,2,…,D),负值数量记为n2d(d=1,2,…,D)。

4)将粒子数量较少的一侧,按照较多一侧的位置使用式(24)变换,更新粒子位置。
(24)
算法步骤如下:
1)随机初始化粒子群,将粒子群分为主、辅2个子群,初始化粒子的速度与位置。
2)根据2.1节所述方法部署骨干节点,对比主、辅子群的适应度值,评估种群的当前最优解及全局最优解。
3)分别更新主、辅子群的速度与位置。
4)度过周期T后检测环境是否发生变化,评估当前部署方案能否满足网络连通性及用户需求量,若不满足,则主子群采取空间对称位移映射,转步骤2)。
5)算法是否达到运行次数,不满足则转步骤2)。
6)算法结束,记录输出值。
3 仿真实验与结果分析
本文实验的开发与仿真环境为Visual Studio 2013,使用VC++编写,参照著名的WMN实验床Roofnet实验网络平台来设置参数,该实验平台由麻省理工大学搭建,取节点覆盖半径为150,节点通信半径为250,节点接入容量为54,UDN的带宽需求值为10,最大跳数为4。实验硬件环境为Intel Core i3 M370 2.4 GHz,2.0 GB内存,操作系统为Windows 7 Ultimate。模拟现实情况生成UDN集合及MRC集合,设置周期时间为15 min,每次环境变化中UDN的变化量是一个[0,udn_count/8]之间的随机整数,每个UDN的坐标可以在场景内随机移动。按照场景规模、MRC数量、MG数量、UDN数量的顺序,依次生成场景1~7为(200×200,10,1,15),(300×300,20,1,25),(400×400,40,2,45),(600×600,80,3,80),(800×800,150,4,110),(1 000×1 000,200,8,140),(2 000×2 000,450,16,360)。正态分布场景下的静态与动态部署结果见表1,平均分布场景下的静态与动态部署结果见表2。

表1 正态分布场景下的静态与动态部署结果

表2 平均分布场景下的静态与动态部署结果
通过上述实验结果可知,本文算法在均匀分布和正态分布情况下以及在动态环境的变化中,MR部署方案中的MR部署数量均能接近静态部署结果,证明了本文算法的有效性。
4 结束语
本文提出一种动态环境下无线Mesh网络骨干节点部署的优化算法,以满足用户带宽需求和网络连通性为前提,使用粒子群算法筛选网关位置,并以最小化路由器数量为目标逐步添加权重最大的相邻节点完成部署。本文研究运用对称位移映射的TSDPSO算法适应动态环境,从新周期开始,检测环境变化,调整节点部署位置以适应需求变化。实验结果表明,该算法能在动态环境中得到有效的部署方案。但本文算法没有考虑节点之间的干扰以及无线网络的可靠性,下一步将对此进行改进。
[1] BENYAMINA D,HAFID A,GENDREAU M.Wireless mesh networks design——a survey[J].IEEE Communica-tions Survey & Tutorials,2012,14(2):299-310.
[2] 吴文甲,杨 明,罗 军.无线Mesh网络中满足带宽需求的路由器部署方法[J].计算机学报,2014,37(2):344-355.
[3] 黄书强,王高才,单志广,等.智慧城市中无线网络节点部署优化方案研究[J].计算机研究与发展,2014,51(2):278-289.
[4] 凌 权,李枚毅.无线Mesh网络中骨干节点部署算法研究[J].计算机工程,2015,41(11):147-152.
[5] XHAFA F,SANCHES C,BAROLLI L.Genetic algorithms for efficient placement of router nodes in wireless mesh network[C]//Proceedings of the 24th EEE International Conference on Advanced Information Net-working and Applications.Perth,Australia:IEEE Press,2010:465-472.
[6] XHAFA F,SANCHES C,BAROLLI L.Local search methods for efficient router nodes placement in wireless mesh networks[J].Journal of Intelligent Manufacturing,2012,23(4):1293-1303.
[7] YANG Shengxiang.A Clustering Particle Swarm optimizer for locating and tracking multiple optima in dynamic environment[J].IEEE Transactions on Evolutionary Computation,2010,14(6):959-974.
[8] REZGUI J,HAFID A,GENDREAU M.Distributed admission control in wireless mesh networks:models,algorithms,and evaluation[J].IEEE Transactions on Vehicular Technology,2010,59(3):1459-1473.
[9] WANG Junfang,CAI Kan,AGRAWAL D R,A multi-rate based router placement scheme for wireless mesh networks[C]//Proceedings of the 6th IEEE Inter-national Conference on Mobile Ad Hoc and Sensor Systems.Washington D.C.,USA:IEEE Press,2009:100-109.
[10] SAKAMOTO S,KULLA E,ODA T,et al.A comparison study of simulated annealing and genetic algorithm for node placement problem in wireless mesh networks[J].Journal of Mobile Multimedia,2013,9(1/2):101-110.
[11] LIN Chuncheng.Dynamic router node placement in wireless mesh networks:a PSO approach with constriction coefficient and its convergence analysis[J].Information Sciences,2013,232:294-308.
[12] 刘子坤,李枚毅,张 晓.动态环境下运用对称位移映射的PSO算法[J].计算机工程,2014,40(11):200-204.
[13] EBERHART R C,SHI Yuhui.Tracking and optimizing dynamic systems with particle swarms[C]//Proceedings of Congress on Evolutionary Computation.New York,USA:IEEE Press,2001:94-97.
[14] KENNEDY J,EBERHART R C.Particle swarm optimiza-tion[C]//Proceedings of IEEE International Conference on Neural Networks.Washington D.C.,USA:IEEE Press,1995:1942-1948.
[15] HERNANDEZ P N,CORONA C C,PELTA D A.Efficient multi-swarm PSO algorithms for dynamic environments[J].Memetic Computing,2011(3):163-174.

