基于异类近邻的支持向量机加速算法
陈景年,胡顺祥,徐 力
(a.山东财经大学 信息与计算科学系,济南 250014; b.鲁南技师学院 商务管理系,山东 临沂 276021; c.济南市公路管理局 信息科,济南250013)
0 概述
支持向量机(Support Vector Machine,SVM)是基于统计学习理论的一种机器学习方法,在结构风险最小化基础上,可有效地避免传统方法中局部极小、过拟合、维数灾难等常见问题,并且在小样本集上依然能取得好的学习效果[1]。因此,在文本分类、网页过滤、目标跟踪等领域得到了广泛应用[2-4]。
标准的SVM训练过程归结为一个凸二次规划问题。 随着训练样本的增多,其训练空间和时间会急剧增加。所以,SVM难以适用于大规模数据集。如何提高 SVM 的学习效率以适应大规模数据处理的需求成为近年来的一个研究热点[5-8]。
本文利用异类近邻来选择边界样本,这一方法不仅适用于复杂边界的情形,而且对多类分类问题也非常有效。
1 研究背景
文献[1]指出,在SVM的训练过程中,只有支持向量对构建分类模型起作用,并且支持向量往往位于类边界附近。因此,边界附近的样本对SVM的分类结果起决定作用。所以在构建SVM分类模型时,不必应用所有训练样本,而只需选取其中最有可能成为支持向量的边界样本参与训练过程。这样,在保持构建的分类模型效果的同时,因训练样本的减少而可以大幅度提高训练效率。
基于上述思路,研究人员给出了一些有效的方法以选取潜在的支持向量来构成精简的训练集,提高了训练效率。
文献[9]利用一个样本分别到2类样本中每个类的中心的距离之比来判断该样本是否为边界样本。该方法在保持SVM分类效果的情况下,可明显提高SVM的训练速度。文献[10]首先用一个小样本子集训练得到一个初始的SVM分类超平面,然后将原样本集中离此平面较远的样本删除。通过该方法可以删除一些冗余样本,在保持SVM泛化能力的同时,提高了其训练速度。
文献[11]利用每个样本的k近邻在训练集中的序号及相应的距离对样本打分,并按打分高低选择样本。文献[12]根据样本的k近邻中异类样本数来选择样本。
近来,文献[13]利用每个样本的最近邻信息得到训练集的一致子集,然后利用此子集训练SVM。该选择算法的效率较高,但有时样本选择效果不够理想。文献[14]以每类样本的聚类中心作为参照来选择其他类中的边界样本。
上述研究工作在保持分类效果和提高训练效率方面都有一定作用,但在数据集的类别边界非常复杂和类别较多的情况下,选择效果往往不理想。
2 基于异类近邻的边界样本选择
为使提出的算法更具普适性,考虑一般的多类分类问题。由于SVM分类模型是针对二类分类问题建模的,因此在应用SVM模型进行分类时,通常将一个多类分类问题转化为多个二类分类问题来解决。常用的转化方式有2种:一对一方式和一对多方式。在一对一方式中,多类中的每2个类之间都要构建一个SVM模型。这样,不仅需要训练大量的模型,而且使后续的分类过程变慢。在一对多方式中,每个类轮流做一次正类。在一个类作为正类时,其余类合起来作为负类。由于一对多方式需训练的SVM模型较少,而且后续的分类过程效率高,因此,在下面的样本选择算法中,将采用一对多方式。
假定训练集A是由L类样本所组成,A中的样本总数为N。A中的每一类样本都轮流做一次正类样本,与此同时,其余样本作为负类样本。下面考虑第c(1≤c≤L)类样本为当前的正类样本时的边界样本选择问题,记选择的结果为Sc。
选择过程包括正类样本选择和负类样本选择2个方面。选择结果Sc初始化为空集φ。首先进行的是负类样本的选择。对于第c类中的每个样本x,计算x在第l(1≤l≤L,l≠c)类中的k个最近邻xlj(1≤j≤k)。判断xlj是否属于Sc。如果xlj∈Sc,则将xlj选入Sc。这里,计算k近邻的操作是在每一小类样本中进行的,不同于传统的做法在整个数据集中进行。因此,上述k近邻的搜索过程因搜索范围的缩小而较传统做法具有更高的效率。
正类样本的选择过程与负类样本选择类似。由于在多类分类问题中采用了一对多的转化模式,这可能会引起正类与负类之间样本数目严重不均衡的问题。因此,在正类样本的选择过程中,增加了一项调节正类和负类之间均衡性的操作,即在正类样本明显偏少的情况下(比如少于选择的负类样本数的一半),则正类样本将全部保留。整个边界样本选择过程如图1所示。其中,L为训练集A中的样本类数,N为A中的样本总数,Nc为第c类样本数,Ns为选择的负例数,Sc为第c类作为当前正类时样本选择的结果。

图1 基于异类近邻的样本选择算法流程
下面是所给的样本选择和模型训练的算法描述。
算法基于异类近邻的样本选择算法
输入训练集A(含有L个类,共N个样本),近邻数k
输出对每个类别c(1≤c≤L),输出以c类样本为正类,其余样本为负类时的选择结果Sc
1)初始化:c=1;Sc←φ。
2)以c类样本为正例,其余样本为负例。
3)负例(即负类样本)的选择过程:
(1)l=1;
(2)如果l≠c,则:
①对于第c类中的每个样本x,计算x在第l类中的k个最近邻xlj(l≤j≤k)。
②如果xlj∈Sc,则Sc←Sc∪{xlj}。
(3)l←l+1;
(4)如果l≤L,则转(2),否则转4)。
4)正例(即正类样本)的选择过程:
(1)比较c类样本数Nc和选择的负例数Ns的大小关系。
(2)如果Nc<0.5Ns,则所有c类样本被选入Sc,转5)。
(3)对每个负例y:
①计算y在第c类中的k个最近邻xcj(l≤j≤k)。
②如果xcj∈Sc,则Sc←Sc∪{xcj}。
5)在得到的Sc上训练SVM模型。
6)c←c+1。
7)如果c≤L,转2)。
8)结束。
3 算法说明
3.1 与相关算法的不同之处
尽管上述基于异类近邻的边界样本选择算法利用了样本的k近邻来进行样本选择,但与以往基于k近邻的样本选择方法相比,本文所给算法有如下不同之处:
1)以往基于k近邻的算法往往是在整个训练集中搜索一个样本的k近邻,而上述算法是在除当前正类之外的每个小类中搜索一个正类样本的k近邻,简称异类k近邻。因此,搜索的效率会明显提高。
2)与以往基于k近邻的算法相比,在上述算法中,异类k近邻的使用使得选择算法能够适用于各种复杂的类别边界,而不像以往算法往往受边界条件的限制。
3)在正类样本的选择过程中,能够根据正类与负类样本数的差距来消除正、负类之间的不均衡问题,这也是上述算法的一个独到之处。
3.2 算法的复杂度分析
所给算法包含了负例选择和正例选择2个过程,并且正例选择过程的复杂度不超过(许多情况下远低于)负例选择过程的复杂度。所以,这里只对负例选择过程的复杂度进行分析。

3.3 算法的参数设置方法
在给出的样本选择算法中,一个样本的近邻数k对算法的效果和效率具有重要的作用。很显然,k越小,选择的样本越少,训练效率会越高。同时,也越容易损失一些支持向量,易引起训练效果的下降。反之,k越大,越不容易漏掉支持向量,但也往往会选入一些冗余的样本,不仅使选择的样本增多,训练效率降低,同时,较多的冗余样本也会降低训练效果。因此,k的值不宜过大或过小,而应在一定的范围内寻找合适的k值。实验发现,绝大多数情况下,在2~10的范围内即可找到一个理想的k值。因此,通过实验不难确定合适的k值。
4 实验结果与分析
为验证本文所给算法的有效性,将它与性能显著的2个边界样本选择算法NPPS[12]以及FCNN[13]进行多方位的比较,具体包括如下3个方面:1)样本选择的效果,即利用选择的样本得到的分类模型的分类准确率;2)选择的样本占总训练样本的比例;3)利用选择的样本训练分类模型所需的时间。
4.1 实验数据集
实验共采用了12个数据集,其中6个为小规模数据集,另6个为中等规模或大规模数据集。它们大都来自于UCI的机器学习数据库[15]。另外,为了验证所给算法对多类分类,特别是大类别数据集分类的效果,实验中还采用了一个包含3 755类的手写中文字符数据集HCL2000[16]。其中每一类都包含1 000个样本,被分成了700个训练样本和300个测试样本。实验中选取了其中的前100个类中的样本,并通过提取8-方向梯度特征得到512个属性。表1列出了每个实验数据集中包含的样本数、属性数(也称为特征数)以及类数。其中,第1个~第6个数据集为小规模数据集,其余6个为中等或大规模数据集。
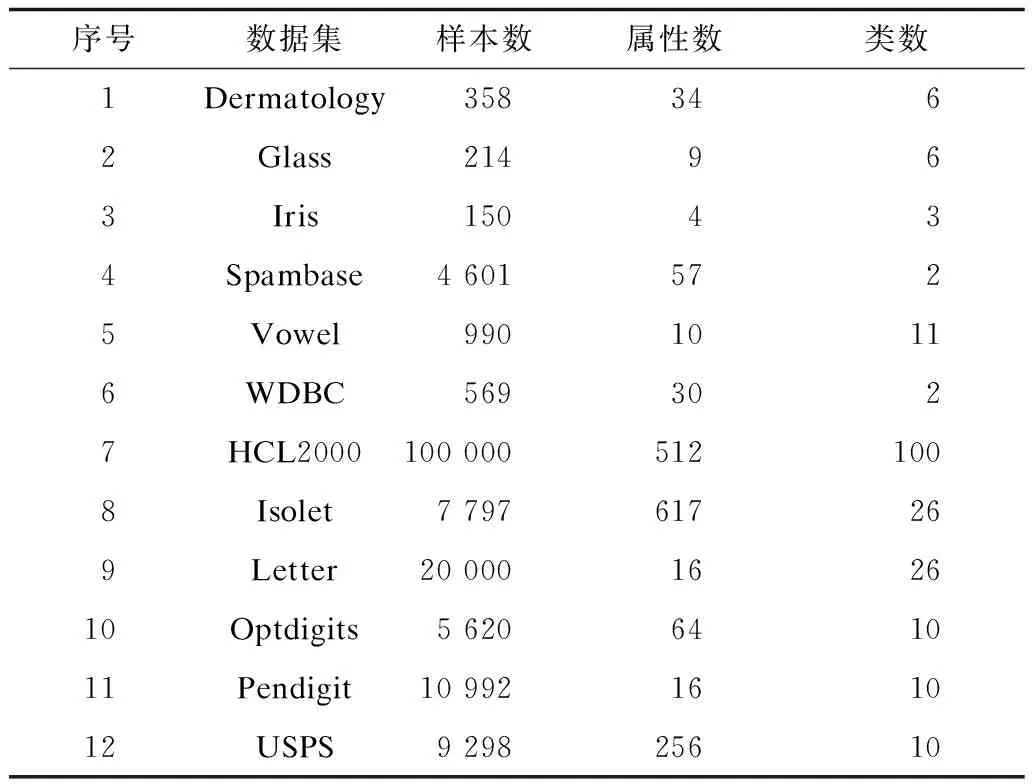
表1 实验数据集参数
4.2 实验参数
在所有SVM模型的训练过程中,采用了下式定义的高斯核函数。
k(xi,xj)=exp(-‖xi-xj‖2/2σ2)
(1)
除了大类别集的数据集HCL2000[16]外,在每个数据集上都采用5重交叉验证的方法进行实验。由于原始的数据集HCL2000规模很大,且已被分成了训练集和测试集,这里没再对其重新划分。
在每个数据集上,对式(1)中高斯核函数的参数σ2、SVM模型的误差限C、本文所给算法的异类近邻数k以及NPPS算法[12]中的近邻数kn都通过实验的方法进行优化。表2列出了在每个数据集上的具体参数取值。由于FCNN[13]中采用的是最近邻算法,因此不需要对其进行参数设置。

表2 在每个数据集上的参数取值
4.3 实验结果
表3列出了在6个小规模数据集上的分类准确率、样本选择比例及训练时间。表4则给出了在其余6个中等或大规模数据集上的实验结果。为了直观地对所给算法与FCNN以及NPPS进行比较,图2~图7用折线图描绘了它们分别在2组数据集上的分类准确率、样本选择比例及样本选择后的训练时间与未进行样本选择的训练时间之比。

表3 在小规模数据集上的实验结果

表4 在中等或大规模数据集上的实验结果
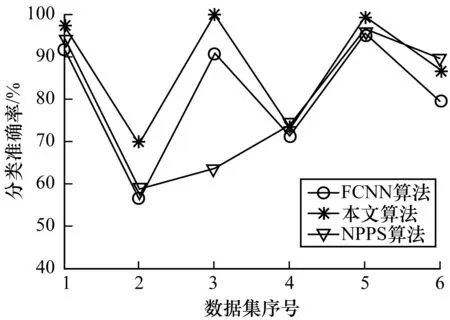
图2 小规模数据集上的分类精度

图3 中大规模数据集上的分类精度

图4 小规模数据集上的样本选择比例
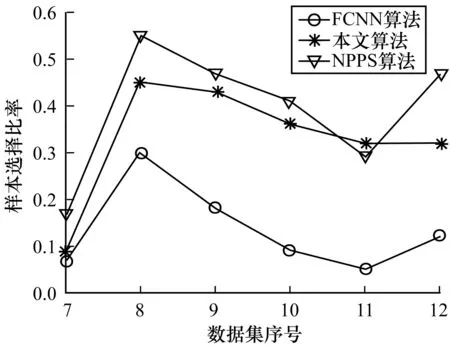
图5 中大规模数据集上的样本选择比例

图6 小规模数据集上的训练时间比

图7 中大规模数据集上的训练时间比
由图2和图3可以直观地发现,在大部分小规模数据集和所有中等规模与大规模数据集上,本文提出的样本选择算法在提高了SVM的训练效率的同时,使分类取得了最好的效果。从表3和表4可以发现,在实验的每个数据集上,本文算法的分类效果没有明显的降低。甚至在HCL2000、Optdigit以及Pendigit等数据集上分类准确率比未进行样本选择的情况下还有所提高。相比之下,FCNN算法与NPPS算法都没有很好地保持分类效果。例如在Dermat、Glass、Iris、WDBC等数据集上,FCNN使得分类精度明显下降。NPPS在Glass、Iris、Letter等数据集上引起了分类效果的明显降低。上述实验结果表明,本文给出的选择算法在选择效果上有着明显的优势。
由图4和图5可以发现,本文所给算法选择的样本的比例总体上略低于NPPS算法的选择比例而高于FCNN算法。在比较的样本选择算法中,FCNN算法选择的样本比例最低,在降低训练数据规模上具有一定优势。但由上文对选择效果的比较来看,FCNN算法容易引起分类效果明显降低。这说明选择的样本并不是越少越好。
从图6和图7综合来看,在提高训练效率方面本文所给算法和NPPS算法相当,而FCNN算法在这方面具有一定优势。这同样是由于FCNN算法选择的样本比例较低的缘故。
5 结束语
在众多的分类算法中,支持向量机(SVM)因其较高的分类精度和坚实的理论基础而倍受关注,在诸多的应用领域中取得了显著的分类效果。然而,SVM对于样本数目来说,具有立方级的训练复杂度。因此,如何提高SVM的训练效率一直是机器学习研究中的热点问题。
为了在保持SVM效果的同时提高其效率,本文给出了精简训练集的一种算法,即利用异类近邻来选择边界样本。这一算法不仅适用于复杂边界的情形,也可以有效地用于多类分类问题,而且能在很大程度上减轻不均衡数据对分类模型的影响。在多个实验数据集上的实验结果表明,该算法在使训练效率大幅提高的同时,能更好地保持甚至改善分类效果。
为了使所给算法能更有效地用于大规模数据集,特别是大数据处理,还需要对算法在效率上做进一步改进,这是下一步要做的一项研究内容。
[1] VAPNIK V.The Nature of statistical learning theory[M].New York,USA:Springer,1995.
[2] JOACHIMS T.Text categorization with support vector machine:learning with many relevant features[C]//Proceedings of the 10th European Conference on Machine Learning.New York,USA:ACM Press,1998:137-142.
[3] 王宪亮,吴志刚,杨金超,等.基于SVM一对一分类的语种识别方法[J].清华大学学报(自然科学版),2013,53(6):808- 812.
[4] 孙俊涛,张顺利,张 利.基于联合支持向量机的目标跟踪算法[J].计算机工程,2017,43(3):266-270.
[5] DONG Jianxiong,KRZYZAK A,SUEN C Y.Fast SVM training algorithm with decomposition on very large data sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(4):603-618.
[6] LI Boyan,WANG Qiangwei,HU Jinglu.Fast SVM training using edge detection on very large datasets[J].IEEE Transactions on Electrical and Electronic Engineering,2013,8(3):229-237.
[7] JUNG H G.Support vector number reduction: survey and experimental evaluations novel[J].IEEE Transactions on Intelligent Transportation Systems,2014,5(2):463-476.
[8] 包文颖,胡清华,王长忠.基于多粒度数据压缩的支持向量机[J].南京大学学报(自然科学版),2013,49(5):637- 643.
[9] 焦李成,张 莉,周伟达.支撑矢量预选取的中心距离比值法[J].电子学报,2001,29(3):383-386.
[10] 李红莲,王春花,袁保宗,等.针对大规模训练集的支持向量机的学习策略[J].计算机学报,2004,27(5):715-719.
[11] PANDA N,CHANG E Y,WU Gang.Concept boundary detection for speeding up SVM[C]//Proceedings of International Conference on Machine Learning.New York,USA:ACM Press,2006:681-688.
[12] SHIN H,CHO S.Neighborhood property based pattern selection for support vector machines[J].Neural Computation,2007,19(3):816-855.
[13] ANGIULLI F,ASTORINO A.Scaling up support vector machines using nearest neighbor condensation[J].IEEE Transactions on Neural Networks,2010,21(2):351-357.
[14] CHEN Jingnian,ZHANG Caiming,XUE Xiaoping,et al.Fast instance selection for speeding up support vector machines[J].Knowledge-based Systems,2013,45(6):1-7.
[15] HETTICH S,BLAKE C L,MERZ C J.UCI repository of machine learning databases[EB/OL].[2017-03-21].http//www.ics.uci.edu/ ~mlearn/MLRepository.html.
[16] ZHANG Honggang,GUO Jun,CHEN Guang,et al.HCL2000——a large-scale handwritten Chinese character database for handwritten character recognition[C]//Proceedings of the 10th International Conference on Document Analysis and Recognition.Berlin,Germany:Springer,2009:286-289.

