基于多级Haar小波变换与KS统计的突变点快速探测方法

宋巧红,齐金鹏,张 煜

(东华大学 信息科学与技术学院,上海 201620)

0 概述

在数据挖掘和统计领域,时序数据突变点的检测已经引起了广泛的关注[1-2],大部分方法是通过比较时间序列样本在过去和现在的概率分布来检测的[3],这种根据分布的不同来检测出异常点的方法灵活性较差[4-6]。在统计方面,已经探索出了一些用于突变点检测的方法,比如KS统计理论[7]。KS统计理论是一种非参数的统计理论,其量化了样本的经验分布函数和参考分布的累积分布函数之间的距离,尤其是两样本的KS检验方法,被广泛用于比较2个样本,因为它对2个样本的经验分布函数的位置和形状参数的差异特别敏感[8]。另一方面,小波变换对于异常点的检测有很好的前景。小波变换可以很容易地从不同的时间或空间距离上提取数据的分布特征[9]。小波分析的核心是多分辨率分析,可以把其中一个信号分解成不同大小的分辨率级别的子信号。小波的定位、正交性和多速率滤波等特性是对信号平稳性和瞬态性分析必不可少的条件[10]。

然而,这些方法大多很耗时,且由于时间复杂度的问题并不适合处理分析大数据[11]。此外这些方法对于一些无效的波动不是很敏感,尤其是2个端点附近的突化。为了实现对时间序列检测的及时性[12-13],本文在多级Harr小波变换与KS统计理论的基础[14-15]上提出一种新的快速探测突变点的理论框架,简称HWKS(Haar Wavelet and KS),并与HW方法、T方法和KS方法从耗时、命中率、误差以及准确度4个方面进行比较。

1 HWKS的理论框架

HWKS的框架结构如图1所示。首先以正常的序列X作为参考序列,然后对其和待检测序列Z通过多级Haar小波变换,分别构建均值二叉搜索树(TcA)和差值二叉搜索树(TcD)。其次,用改进的KS统计理论对TcA中的根节点到叶子节点中的异常点进行快速检测。最后,对模拟的时序数列进行突变点检测,以验证该方法的有效性。

图1 HWKS突变点检测过程

1.1 均值二叉搜索树和差值二叉搜索树的构建

一般而言,可利用多级Haar小波变换方法,将离散的时序信号Z={z1,z2,…,zN}解析成不同的频域分量,并表示如下:

(1)

其中,cA和cD分别为均值参数和差值参数。多分辨率分析(Multi-Resolution Analysis,MRA)是小波分析的核心[16],根据MRA,可以概念化小波变换的过程,将总体的N分解成一小段一小段n。向量vi和wi分别代表缩放信号和小波基向量。离散信号Z的均值信号Ak和差值信号Di可以表示为:

(2)

Ak= (Z·Vk)Vk=

(3)

(4)

因此,可以得到如下方程:

(5)

Ak=cAk·Vk=

(6)

Dk=cDk·Wk=(cDk,1,cDk,2,…,cDk,N/2k)·

(7)

因此,可将时序数据Z分解成多维的均值参数矩阵(McA)和差值参数矩阵(McD):

(8)

其中,0≤k≤m=lbN,1≤j≤N/2k。

综上,可将时序数据Z分解成多维的均值参数矩阵(McA)和差值参数矩阵(McD)。然后,将参数矩阵McA和McD分别映射到对应的均值二叉搜索树(TcA)和差值二叉搜索树(TcD)的各层子节点。分别通过McA和McD来构造TcA和TcD中的各级非叶子节点。同时,叶子节点直接来自Z中的元素。多级Harr小波变换将待检测的序列Z分解成TcA和TcD的过程,如图2所示。

图2 待检测序列的Z分解

1.2 基于改进KS统计理论的HWKS

KS统计是一种非常有用的非参数方法,被广泛应用于2个样本的比较。它对2个样本的经验分布函数的位置和形状参数的差异都特别敏感。假定一个时间序列Y={y1,y2,…,yN},可以表示为Y=f(i/N)+X,i=1,2,…,N,其中X={xi}i=1,2,…,N是独立同分布的随机变量,f是未知分布的噪声信号。那么,就可以用分布函数Fm(x)来表示正常的时间序列X,同时用分布函数Gn(x)来表示异常的时间序列Y。待检测的时间序列Z表示如下:

Z= {X,Y}={Z1,Z2}=

{z1,z2,…,zc,zc+1,zc+1,…,zn}

为了检测Z中的突变点,可以通过改进的KS统计理论来评估X分布和Z分布之间的距离,如式(9)所示。

(9)

(10)

(11)

可以表示Z中的第j个元素zj,同时在HWKS方法中定义一个新的元素zk,j:

(12)

(13)

其中,cAk,j是TcA中的非叶子节点,zk,j是根据cAk,j新定义的元素,且1≤j≤N/2k,a=2k(j-1)+1,b=2k×j。

可以为HWKS定义一个改进的KS统计理论方法:

(14)

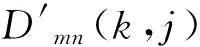
H0:Fm=Gnvs.H0:Fm≠Gn

(15)

为了检验H0,制定一个策略:

(16)

1.3 HWKS框架的异常点搜索策略

为了检测时间序列Z的突变点,需要在TcA的根节点和叶子节点之间建立一条准确和快速的最优路径。第1个搜索策略如下所示:

策略1假定 TcA中的非叶子节点是cAk,j,它左面的子节点和右面的子节点分别是cAk-1,2j-1和cAk-1,2j。

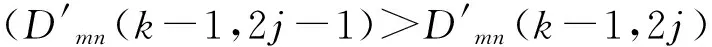
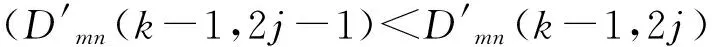
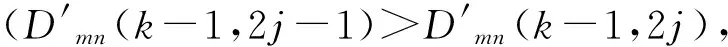
1)如果满足|cDk-1,2j-1|>|cDk-1,2j|,选择TcA中的左侧子节点cAk-1,2j-1作为当前的搜索路径。

2)如果满足|cDk-1,2j-1|<|cDk-1,2j|,选择TcA中的右侧子节点cAk-1,2j作为当前的搜索路径。

2 实验结果与分析

通过仿真的时序数据来评估HWKS的可行性,先对仿真数据进行一次检测,再对仿真数据进行多次检测。最后,设置不同的样本长度和突变点位置,对每组数据都进行400次重复实验,通过与KS方法、HW方法和T方法的比较来分析HWKS方法的耗时、命中率、误差和准确度。

2.1 对数据的一次检测

图3为模拟的待检测时序数据。每个待检测的时序数列Z的长度都为N,由2个部分组成,一部分为正常的时序数列,长度为K,正常的序列服从均匀分布;另一部分为不正常的序列,长度为NK,通过数据拼接的方式,将均匀分布替换为服从高斯分布的序列。图3中数据的长度为32,突变点的位置为6。

图3 模拟的待检测时序数据

用这4种方法对图3 的时序数据进行检测,检测结果如图4所示。为了更加清楚地查看检测结果,将图4的数据整理在表1中。

图4 4种方法的检测结果

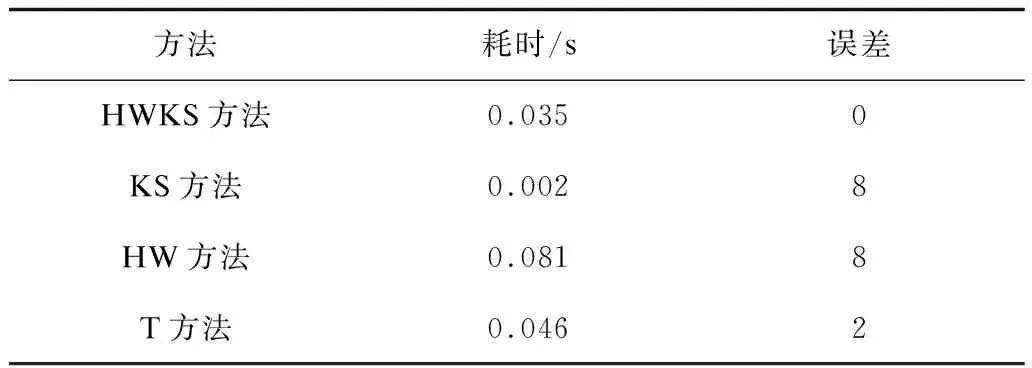
方法耗时/s误差HWKS方法0.0350KS方法0.0028HW方法0.0818T方法0.0462

从表1可以看出,HWKS的误差最小,耗时相对较小。KS虽然耗时较小,但是误差很大。HW耗时较长,T方法的误差比HWKS方法大。所以,综合考虑,HWKS在这4种方法中,效果最好。

2.2 对不同突变点不同数据长度的多次检测

先设置一个固定的突变点,待检测样本的长度N=128,K=111。通过40次的仿真实验来检测突变点的位置。图5(a)～图5(d)为对数据进行处理后的分布,图5(e)～图5(h)为对检测到的不同位置的突变点的位置进行拟合,从图中可看出命中的突变点的大概位置。

图5 多次仿真的实验结果

为了更加清楚地查看检测结果,将数据整理在表2中。对同一个突变点进行多次检测时,可以发现HWKS方法的准确度最高,耗时最小。为了进一步验证HWKS方法的可行性,设置了样本的不同长度,并设置不同的突变点位置,对检测的时间长短、命中率、误差和准确度进行检测。检测结果如表3所示。并将表3中各个指标的平均值整理在表4中。

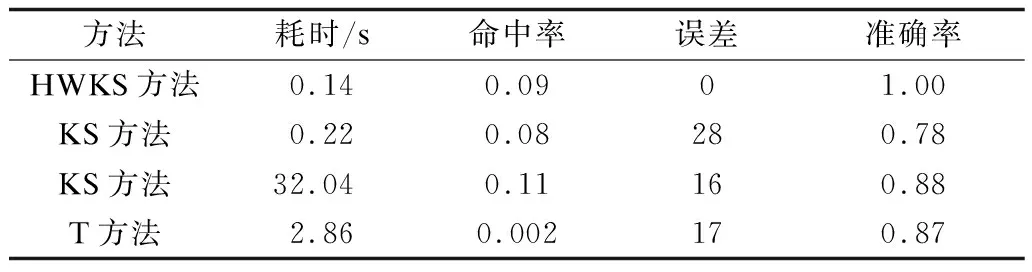
表2 多次仿真的实验数据

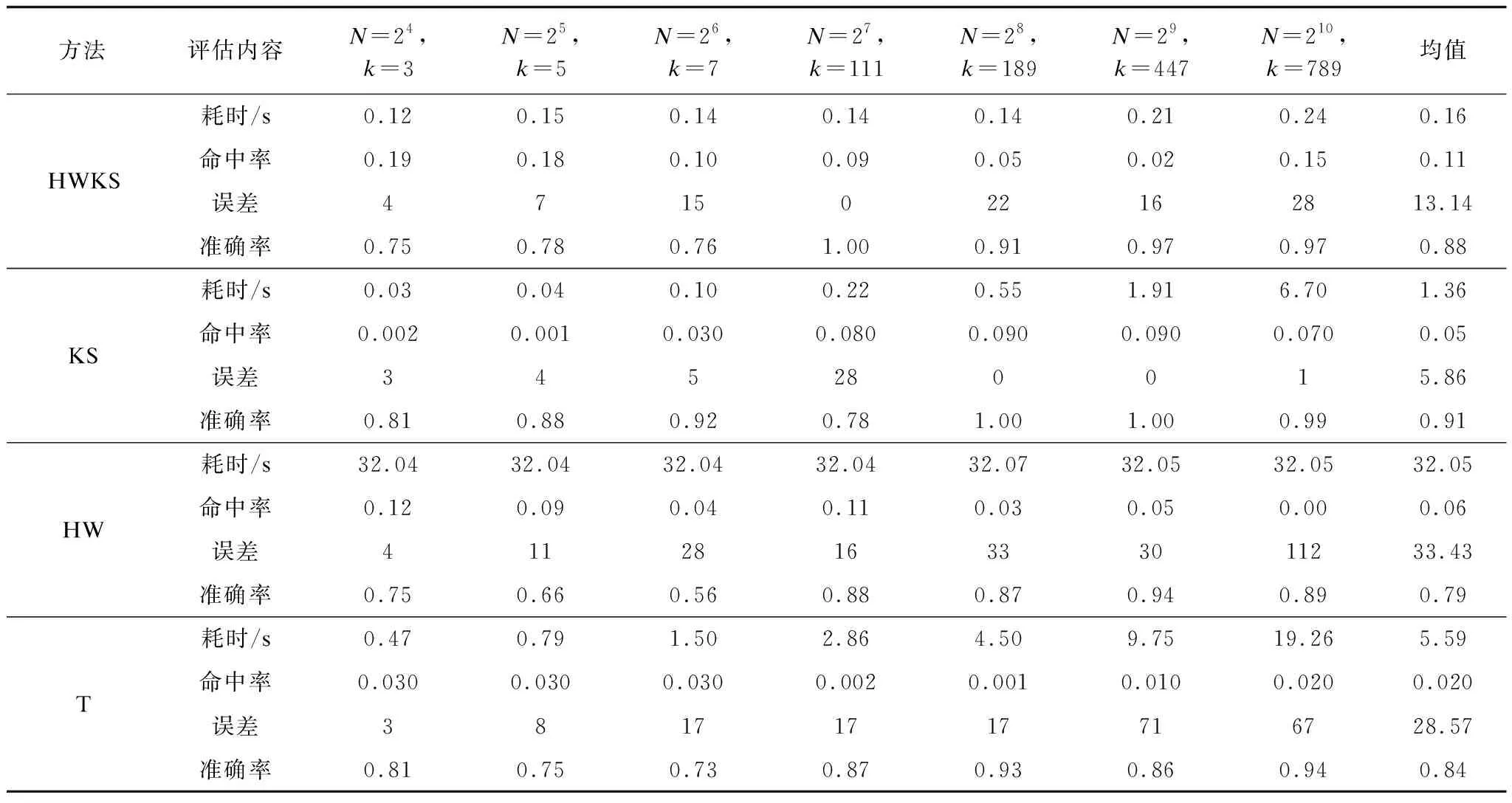
表3 多次检测结果的时间、命中率、误差、准确度

表4 多次统计的平均值

从统计的平均值可以看出HWKS方法的准确度相对较高,虽然KS的准确度较高,但是耗时比HWKS要大很多。当样本的尺寸较小,且突变点发生在左边界或者右边界时,HWKS的命中率要比KS高。

相比于HWKS方法和KS方法,在检测突变点时,HW方法需要耗费更多的时间,而且命中率不是很高。

表3的结果表明,HWKS对于具有较小尺寸N的样本的左边界和右边界附近的较小显著数据波动具有更好的性能和灵敏度,由于计算时间较短,命中率较高,因此HWKS是用于模拟时间序列上的突变点检测的较好方法。

3 结束语

本文结合多级Haar小波变换与KS统计理论,给出对时序数据突变点的快速探测方法HWKS。该方法主要利用多级Haar小波变换与KS统计理论,对标准参考序列以及待检测序列分别构建均值二叉搜索树(TcA)和差值二叉搜索树(TcD)。并基于改进的KS检验方法提出二叉树搜索的2种策略,进而完成对时序数据突变点的快速检测的HWKS理论框架的构建。最后,用模拟的时序数据进行验证,结果表明,与HW方法、T方法和KS方法相比,HWKS方法在对突变检测时的误差较小,用时最短,准确度较高。综合考虑,HWKS方法是对突变点进行检测的一种有效的方法。

[1] 李国杰.大数据研究的科学价值[J].中国计算机学会通讯,2012,8(9):8-15.

[2] 蒋 涛,冯玉才,朱 虹,等.时序数据挖据概述[EB/OL].[2017-04-14].http://doc.mbalib.com/view/8f6ae3ed41ef4cd4ec9207ae75d1cbf8.html.

[3] 秦首科.数据流上的异常检测[D].上海:复旦大学,2006.

[4] MANIKOPOULOS C,PAPAVASSILIOU S.Network intrusion and fault detection: a statistical anomaly approach[J].IEEE Communications Magazine,2002,40(10):76-82.

[5] 文 琪,彭 宏.小波变换的离群时序数据挖掘分析[J].电子科技大学学报,2005,34(4):556-558.

[6] 侯澍旻.时序数据挖掘及其在故障诊断中的应用研究[D].武汉:武汉科技大学,2006.

[7] 侯澍旻,李友荣,刘光临.一种基于KS检验的时间序列非线性检验方法[J].电子与信息学报,2007,29(4):808-810.

[8] WANG Yao,WU Chunguo,JI Zhaohua,et al.Non-parametric change-point method for differential gene expression detection[EB/OL].[2017-04-14].https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3104986/.

[9] 王小宜,卢正鼎,凌贺飞.一个基于小波的时序数据异常探测的新算法[J].计算机工程与科学,2005,27(6):83-85.

[10] LIN H D.Automated visual inspection of ripple defects using wavelet characteristic based multivariate statistical approach[J].Image and Vision Computing,2007,25(1):1785-1801.

[11] 刘丹红,张世英.基于小波神经网络的非线性误差校正模型及其预测[J].控制与决策,2006,21(10):1114-1118.

[12] LIN J,KEOGH E,LONARDI S,et al.A symbolic representation of time series,with implications for streaming algorithms[C]//Proceedings of ACM Sigmod Workshop on Research Issues in Data Mining & Knowledge Discovery.New York,USA:ACM Press,2003:2-13.

[13] 钟清流,蔡自兴.基于统计特征的时序数据符号化算法[J].计算机学报,2008,31(10):1857-1864.

[14] SHARIFZADEH M,AZMOODEH F,SHAHABI C.Change detection in time series data using wavelet footprints[C]//Proceedings of International Symposium on Spatial and Temporal Databases.Berlin,Germany:Springer,2005:127-144.

[15] BRODSKY B E,DARKHOVSKY B S.Nonparametric methods in change point problem[M].Berlin,Germany:Springer,1993.

[16] ALARCON-AQUINO V,BARRIA J A.Anomaly detection in communication networks using wavelets[J].IEEE Proceedings Communications,2002,148(6):355-362.