基于重要节点删除法的社会网络层次结构分析
王 魁,马 宏,黄瑞阳
(国家数字交换系统工程技术研究中心,郑州 450002)
0 概述
社团结构是复杂网络中的重要结构[1],一个最优的社团划分方法是将所有同一属性的节点划到同一类,不同属性的节点划到不同类中。由于大多数网络无法预知各节点的属性,因此传统的社团发现方法将连边密集的节点划为一个社团,连边稀疏的划为不同社团[2],如文献[3]提出的GN算法、FN算法[4]与文献[5]提出的Fast Unfolding算法等。然而,随着研究的深入,研究者发现当节点增多时,社团结构互相融合,使网络不再有最优的划分[6]。这是由于现实网络中节点根据重要程度不同呈现层次性关系[7],一些重要节点同时连接了多个社团,使得不同社团之间的界限不再明显,根据连边疏密对网络划分的方法不能得到最优的划分结果。因此,有学者提出使用网络分解方法来分析网络的结构。
网络分解方法最早由文献[8]提出,他们首先验证了现实网络具有无标度性,然后分别把随机网络和无标度网络置于2种类型的打击策略之下:随机移除网络中的节点和选择性移除度数最高的节点,发现无标度网络在选择性攻击下更容易崩溃。2014年,文献[9]提出了SlashBurn方法,将网络分解与邻接矩阵重排序结合起来,实现对大规模网络的压缩,但是该方法局限于将网络快速分解,没有分析网络分解过程中产生的分支在网络结构的作用。文献[10]在此基础上提出的MTP方法分析了删除部分中心节点后对网络结构产生的影响,通过对删除部分中心节点后的网络进行社团划分,得出了更好的网络划分效果,但是该方法没有找出所有使不同社团连接的节点,因此,没有根本解决现实网络中无最优划分的问题。
上述网络分解方法都是使用度数作为节点重要性的衡量方法,没有比较使用其他中心指标的中心节点删除后对网络的影响。节点重要性可以用多种指标来衡量[11],如度、介数、k-shell、pagerank等,不同的指标在描述节点重要程度时侧重的方面各有不同。度中心性[12]认为一个节点的邻居越多则影响力越大,这是描述节点重要性最简单的指标,度中心性计算简单但忽略了节点的全局特征。因此,在以度为中心指标分解网络时会使社团自身分解。介数中心性[13]是基于网络全局属性的指标,介数越高的节点越容易成为不同社团之间的桥节点,因此以介数为中心指标分解网络可以使网络以社团为单位分解,然而,介数中心性的计算时间复杂度较高,需要改进算法来提高计算节点介数的算法效率。
为利用节点的层次性特征分析社会网络结构,本文提出一种改进的基于重要节点删除的网络分解方法对网络结构进行划分。
1 相关工作
1.1 节点介数定义
用图G=(V,E)表示一个网络,其中,V表示所有节点集合,E表示所有边集合,用σst表示从节点s到节点t的最短路径数量,σst(v)表示从节点s到节点t的最短路径中经过节点v的数量,δst(v)表示节点s到节点t的最短路径中经过节点v的比例,即:
用δs·(v)表示从s到所有其他节点的最短路径中经过v的比例,即:
一个节点的介数中心性可以表示为所有最短路径中经过该节点的最短路径所占比例,定义为:
(1)
用传统方法计算介数的时间复杂度为O(n3),n为网络中节点数量。随着网络规模的增加,减少算法的计算复杂度成为亟待解决的问题。
1.2 图的连通分支
在一个无向图G中,若从顶点vi到顶点vj有边相连,则称vi和vj是连通的,如果图中任意两点都是连通的,那么图被称为连通图[14],否则,称该图为非连通图。图G中的一个极大连通子图称为G的连通分支,连通分支中包含的节点数极大,即没有除了连通分支外的其他节点与该连通分支相连。连通图只有一个连通分支,即其自身,非连通图有多个连通分支。
在现实网络中,同一社团内的节点具有相似性从而容易产生连边,因此,一般处在同一个连通分支中。不同的社团通过一些中心节点的连接而合并到同一个连通分支中。还有一些孤立节点,如微博中刚注册的账号,可以通过关注推荐的中心节点加入连通分支,或者关注自己现实中的好友加入社团从而并入连通分支。因此,现实网络中的大多数节点都处在同一个最大连通分支[15]中,而通过节点删除的策略可以从网络中分解出多个连通分支。
2 基于重要节点删除的网络层次划分
根据复杂网络中社团之间普遍存在桥节点且删除少量节点可以使网络分解的特点,本文采用基于重要节点删除的网络分解方法对网络层次结构进行分析。
2.1 相关定义
2.1.1 图的邻接矩阵
用邻接矩阵A来表示一个具有n个节点的网络,矩阵中的元素sij表示网络中节点的连接情况,在无权无向图中,若sij=0表示节点i和j没有连接,sij=1表示节点i和节点j有连接。
2.1.2 星型结构及模型
星型结构是一种基本网络结构[16],星型结构中所有节点只和中心节点相连,星型网络结构模型如图1所示。图1(a)给出了星型结构和其邻接矩阵,可见星型结构中的节点分为两类:中心节点和叶子节点,星型结构的邻接矩阵呈倒L型。
定义星型结构模型为一种广义的星型结构,从星型结构到星型结构模型的演化过程中,包含两部分:叶子节点的泛化与中心节点的泛化。
叶子节点的泛化如图1(b)所示,与中心节点相连的节点中有一部分互相连接,即邻接矩阵的对角线上出现块状区域,将互相连接的这部分节点视为一个超级叶子节点。中心节点的泛化如图1(c)所示,网络中增加若干个中心节点,即邻接矩阵网络中出现多个倒L型结构,则将多个中心节点合并为一个超级中心节点。如图1(d)所示,经泛化后的网络仍然可以看作一个星型结构,称为星型结构模型。表1列举出了本文常用符号。

图1 星型网络结构模型

符号描述G(V,E)无权无向网络G,V为节点,E为边size(G)G中的节点个数betweenness(i)节点i的介数hub中心节点hubset所有中心节点的集合CC连通分支branch所有CC组成的分支集合GCC最大连通分支k每次删除的中心节点个数m把CC作为超级叶子节点的最少节点数
2.2 介数计算方法
根据式(1)可以得出,计算一个节点的介数需要计算最短路径数量。显而易见,度数为1的节点到任何一个节点的最短路径都要经过该节点的邻居节点,因此,根据网络中剩余节点即可计算出原网络中节点的介数,同时由于度数为1的节点在网络中不可能成为连接2个社团的节点,因此,没有必要计算它们的介数。基于此,本文提出将度数为1的节点删除,结合原节点度数信息计算剩余网络中节点的介数,从而减少运算复杂度。下文就如何根据剩余网络计算原网络中度数大于1的节点介数给出推导。
对于网络G,用D1表示所有度为1的节点集合,R表示所有度为1的节点的邻居节点集合。删除G中度为1的节点得到G’,G’中节点v的介数表示为:
(2)
任意取一个节点t’∈D1,恢复其到邻居节点t∈R的连接,此时v的介数变为:
(3)
由于从t’出发的所有最短路径都经过t,因此δt·(v)=δt’·(v)。
(4)
同理,当原网络中所有度为1的节点加入后,得到:
(5)
其中,DS表示节点s所连接的度为1的节点个数。
根据文献[17]的研究,现实中大多数网络的节点度数服从幂率分布,即度数越低的节点数量越多,如图2展示的是一个度数服从幂律分布的推特网络rt-alwefaq,在删除度为1的节点后网络规模会大大缩小,因此,本文方法可以有效减少介数计算的时间复杂度。

图2 推特网络的度分布及删除度为1节点后网络规模变化
2.3 基于网络分解的邻接矩阵重排序与网络简化
传统的社团定义是社团内部边密集而社团间稀疏。文献[6]在研究中发现,随着网络规模的增大,社团逐渐与网络中其余部分互连在一起,出现分层、嵌套的现象,使社团间变得不再稀疏,从而不容易分割。为解决社团不易划分的问题,本文从相反的角度出发,先找出这些使不同社团连接起来的节点,再通过删除这些节点使网络分解,则原本通过这些节点相连的社团就会逐个与整体网络分离开,从而达到分析网络结构的目的。如图3所示,将不同社团相连的节点设为中心节点,即hub,在找出并删除hub后,计算剩余GCC中节点的中心性,找出GCC中的hub并删除,对每次产生的GCC做相同操作直到整个网络不可分解,其中,图1(b)、图1(d)节点数为15。对分解过程中产生的一系列分支进行筛选,若CC的规模较小,说明这部分节点在网络中仅与少量的hub相连,可以当作不具代表性的节点;若CC的规模较大,说明这部分节点具有较强的相似性,可以作为网络中一个社团。

图3 网络分解与邻接矩阵重排序
用邻接矩阵重排序来表示上述分解过程,首先将网络表示为邻接矩阵A,再将每次删除的中心节点放在邻接矩阵头部,产生的连通分支按大小顺序放在尾部,直到网络不可分解,详细步骤见算法1。
算法1基于网络分解的邻接矩阵重排序方法
输入网络G的邻接矩阵A,常数k、m
输出重排序后邻接矩阵B
将节点在A中的排列顺序设为A= (hubset;GCC;branch);
初始化:hubset=∅;GCC=A;branch=∅
while size(GCC)>k
for i ∈GCC
根据2.2节算法计算betweenness(i);
end
将节点按betweenness(i)降序排列得V [n];
hub=V(1)~V(k);
hubset=hubset+hub;
计算删除hub后图的连通分支,降序排列得CC[s];
GCC=CC(1);
branch=CC(2)~CC(s)+branch;
B=(hubset;GCC;branch);
return B
由于在邻接矩阵重排序的过程中,本文将中心节点放到了邻接矩阵的头部,因此头部的节点应服从星型结构的倒L型分布,分支放在邻接矩阵的尾部,则尾部节点的邻接矩阵服从社团结构的块状分布。通过重排序后的邻接矩阵,将hub设为超级中心节点,视为在网络中其连接作用的中枢节点,将节点数大于m的CC作为超级叶子节点,视为网络中聚集而成的社团。因此,本文方法可以从原网络中找出社团结构与节点之间的层次关系,从而将原网络简化为一个星型结构模型。
3 实验结果与分析
为进一步验证节点删除法对网络结构分析的效果,将在不同规模的真实网络数据集上测试本文方法。数据集来自斯坦福 SNAP数据集和network repository网站,包括脸书网络和推特网络。具体参数如表2所示。

表2 真实社会网络数据集
3.1 社团属性未知的网络
现实社会网络中节点的属性常常是未知的,为了能更好地展示本文算法在划分一般社会网络结构时的适用性,首先对4个属性未知的社会网络分别使用传统的社团划分方法和几个不同的网络分解方法进行划分,划分的结果以邻接矩阵重排序的形式表示。
从图4~图7可以看出,使用Fast Unfolding算法对网络中的节点进行社团划分,在邻接矩阵中对节点重排序后,节点排列成若干个密集的块状区域,说明这些块中的节点连接密集而块间连接稀疏,形成了社团结构。但是邻接矩阵中除了块状区域,还有一些离散的点分布在块状区域周围,这些节点便是没有得到最优划分的节点,它们在不同的块中存在连接,因此,没有一个公认的标准来判定它们属于哪一个社团。Slashburn方法将网络中度数最高的节点抽取出来,对剩下的分支进行排序,可以看出对网络具有较好的压缩效果,但是删除度数最高的节点之后分支过于零散,不利于分析网络的结构。MTP方法兼顾了Slashburn和传统社团划分方法的优点,删除部分度数最高的节点之后对网络进行社团探测,但对于如何确定删除中心节点的数目没有给出最优的解决方法。因此,仍有部分节点的连接存在于不同社团之间,没有得到正确的划分。本文算法以介数作为节点重要性指标,删除这部分节点后使网络完全分解,根据重排序的结果可以看出,所有网络都可以被总结为星型结构模型,邻接矩阵头部的节点呈现出“倒L型”结构,因此,可以视为一个超级中心节点;对角线上的节点排列成若干个互不相连的块状结构,组成超级叶子节点。使用本文算法对网络进行划分,既可以得出更清晰的社团结构,同时又可以明显看出网络中的层次划分。

图4 rt-copen网络邻接矩阵重排序结果

图5 rt-bahrain网络邻接矩阵重排序结果

图6 rt-alwefaq网络邻接矩阵重排序结果
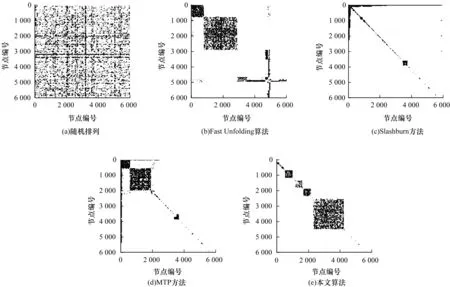
图7 rt-dash网络邻接矩阵重排序结果
3.2 社团属性已知的网络
为了验证本文算法对社会网络结构划分是否具有实际意义,本文使用属性已知的Facebook网络进行验证。
Facebook网络由10个互有交集的个人中心网络组成,同一个节点可能出现在不同用户的朋友圈中。通过用不同方式对邻接矩阵排序,可以直观地看到不同网络结构分析方法的特点。
图8对比了5种按不同的网络邻接矩阵重排序方法得到的结果。

图8 Facebook网络的分解情况
图8(a)是按真实划分得出的排列结果,可以看出以这10个人为中心组成了10个大小不同的朋友圈,每个朋友圈中存在一些影响力较大的节点对在不同朋友圈之中都有影响力。图8(b)说明对网络随机划分无法得到与真实划分相同的划分结果。图8(c)使用传统社团划分方法虽然得到了85%的节点的正确网络划分,但对于不同朋友圈中有较大影响力的节点没有得出正确的划分,这是由于传统的社团衡量指标划分在不同社团之间具有大量连接的节点时还存在局限。图8(d)SlashBurn方法虽然得到了若干个社团结构,但丢失了大部分节点的正确网络划分,划分准确率仅为45%。这是由于度中心性属于局部中心性指标,度数大的节点更容易成为一个社团的核心而非社团之间的连接点,删除度数较大的节点使得原来同一社团内的节点被分解开从而无法得到真实社团结构。图8(e)中MTP方法通过删除一部分度数较大的节点后排除了部分干扰,因此可以看出,其划分效果比传统社团划分方法有了较大的提升,划分准确率达到了89%,但由于MTP方法没有对所有跨社团的节点进行识别,因此仍有部分节点没有得到正确划分。本文算法通过比较不同节点重要性的定义,以介数作为节点在不同社团连接程度的判定标准,将使社团连接的节点删除,得到剩余节点的社团划分,在去除中心节点的情况下,本文算法对剩余节点划分的准确率达到了95%。如图8(f)所示,在网络分解的过程中,邻接矩阵的左侧和上侧组成一个倒L型,说明矩阵头部的中心节点构成了一个星型结构,对角线上依次出现了大约10个正方形块,这10个正方形块没有交集,仅与中心节点连接,构成了星型结构的叶子节点。其中对角线上的矩形块代表以这10个用户为核心的朋友圈,越靠右的正方形块对应的中心节点越少,说明越靠右的节点与整体网络的联系越少。因此,利用分解方法可以得出和原网络一致的社团划分,同时将网络中这10个中心用户以及在不同朋友圈中影响力较大的用户挖掘出来,将中心用户作为中心节点,节点数超过50的分支作为叶子节点,这样原网络可以被总结为一个具有10个叶子节点的星型网络结构,如图8(g)所示。
3.3 算法运行效率
算法的运行效率取决于两个方面,一方面是使网络完全分解时所需删除的重要节点数量,另一方面是每次运行节点删除算法所需的时间。首先将本文算法与Slashburn方法在分解不同网络时所需删除的节点数进行对比,从图9可以看出,本文方法通常只需删除比Slahburn方法少一半的节点就可以使网络完全分解,这说明介数比度更能用来衡量节点在网络结构中的连接作用,删除介数高的节点能更快地使网络分解。
由于在删除节点过程中主要步骤是找到介数最高的节点,而介数的计算复杂度比度数计算要高,因此本文针对大规模网络提出了介数的快速计算方法,根据定义可知介数计算与网络规模有直接关系,本文通过删除度为1的节点使网络规模平均缩小了一半左右,因此介数的计算复杂度大约只有传统方法的12%,图10比较了传统的介数计算方法和本文所提的介数计算方法在每次运行节点删除算法时所需的时间。

图9不同分解方法使网络完全分解时移除的节点数在网络中比例

图10 传统介数计算方法和本文算法的运行时间
通过减少删除节点的次数以及每次删除节点所需的时间,本文算法得到了更高的运行效率。图11对比不同网络结构分析方法划分不同网络的总时间,可以看出,本文算法在不同网络中的表现与其他方法没有较大差别,因此,本文算法在未牺牲计算复杂度的情况下得到了更好的网络划分效果。

图11 不同算法划分网络所用时间
4 结束语
本文将网络分解方法应用到社会网络的结构分析上,并提出一种大规模网络中节点介数的快速计算方法。以介数作为节点重要性指标,运用重要节点删除法对网络进行分解,将分解出的分支和中心节点在网络的邻接矩阵中重排序,发现社会网络中的层次结构。在真实网络数据上的实验结果表明,该方法可以对较大规模的社会网络进行结构分析,能够将网络简化为一种以中心节点为核心、分支为叶子的星型结构模型。与现有的网络结构分析方法相比,本文方法根据少数在网络结构中起重要连接作用的节点,发现了社会网络中的层次结构以及社团性质,避免了传统的社团发现方法中社团定义不明确、没有最优划分等问题。本文方法为研究大规模网络中的结构提供了新的思路,但还需要在不同类型的网络中进行检验,此外,如何将该方法对网络中的节点进行更精细的分类是下一步研究的目标。
[1] 李晓佳,张 鹏,狄增如,等.复杂网络中的社团结构[J].复杂系统与复杂性科学,2008,5(3):19-42.
[2] FORTUNATO S.Community detection in graphs[J].Physics Reports,2010,486(3):75-174.
[3] GIRVAN M,NEWMAN M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.
[4] NEWMAN M E J.Fast algorithm for detecting community structure in networks[J].Physical Review E,2004,69(6).
[5] BLONDEL V D,GUILLAUME J L,LAMBIOTTE R,et al.Fast unfolding of community hierarchies in large networks[J].Journal of Statistical Mechanics Theory and Experiment,2008,2008(10):155-168.
[6] LESKOVEC J,LANG K J,DASGUPTA A,et al.Statistical properties of community structure in large social and information networks[C]//Proceedings of WWW’08.Washington D.C.,USA:IEEE Press,2008:695-704.
[7] 庞 垠.复杂网络社团结构探测方法及社团内节点层次关系研究[D].北京.北京理工大学,2015.
[8] BARABASI A L,ALBERT R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.
[9] KANG U,FALOUTSOS C.Beyond caveman communities:hubs and spokes for graph compression and maining[C]//Proceedings of ICDM’11.Washington D.C.,USA:IEEE Press,2011:121-132.
[10] YONGSUB L,LEE W J,CHOI H J,et al.Discovering large subsets with high quality partitions in real world graphs[C] //Proceedings of International Conference on Big Data & Smart Computing.Washington D.C.,USA:IEEE Press,2015:186-193.
[11] 任晓龙,吕琳媛.网络重要节点排序方法综述[J].科学通报,2014,59(13):1175-1197.
[12] FREEMAN L C.A set of measures of centrality based on betweenness[J].Sociometry,1977,40(1):35-41.
[13] BONACICH P.Factoring and weighting approaches to status scores and clique identification[J].Journal of Mathematical Sociology,1972,2(1):113-120.
[14] PARSONS T D.The search number of a connected graph[C]//Proceedings of the 9th Conference on Combinatorics,Graph Theory,and Computing.Winnipeg,Canada:[s.n.],1978:549-554.
[15] NEWMAN M E J.The structure of scientific collaboration networks[J].Proceedings of the National Academy of Sciences,2001,98(2):404-409.
[16] BORGATTI S P,MEHRA A,BRASS D J,et al.Network analysis in the social sciences[J].Science,2009,323(5916):892-895.
[17] 罗由平,周召敏,李丽娟,等.基于幂率分布的社交网络规律分析[J].计算机工程,2015,41(7):299-304.

