太阳能选择性吸收涂层生产线铝带张力控制的研究

威海太阳能光热吸收薄膜光热科技有限公司 ■ 祝明 张浙军 裴宏伟 陈刚

0 引言

目前的太阳能选择性吸收涂层主要是以0.2～0.4 mm厚的铝带为主，在太阳能选择性吸收涂层的生产中，张力控制起到了十分重要的作用，是保证产品质量和工艺稳定的重要因素。本文以某厂真空镀膜机的卷取部分为研究对象，对其张力控制系统的原理和方法进行详细分析，找出影响张力控制精度的关键问题，并找到解决方案，这对于改善张力控制精度进而提高太阳能选择性吸收涂层的生产效率和产品质量具有积极意义。

1 太阳能选择性吸收涂层生产线中铝带张力控制系统的构成

从张力控制系统的控制方法来分，可将张力控制系统分为直接张力控制系统、间接张力控制系统和复合张力控制系统3种[1]。

1.1 直接张力控制系统

直接张力控制系统通常配备张力检测元件，将测得的实际张力值传输至控制器并与设定的张力值进行比较，再根据算法进行输出控制。该系统的优点是：系统构成简单，能克服卷径、速度及惯性转矩变化等对张力的影响；缺点是：测量的精度主要取决于张力传感器的测量精度，若现场电磁干扰比较严重，张力传感器的测量精度可能会受到影响。

1.2 间接张力控制系统

间接张力控制系统通常无张力传感器，是通过对传动设备各个组成部分进行详细地分析，从而找到影响卷取张力的变量，然后对这些变量进行控制来达到张力控制的目的。间接张力控制系统需要可编程逻辑控制器(PLC)计算铝带的实时卷径，对摩擦转矩和惯性转矩进行计算。该系统的优点是：省略了张力传感器，降低了成本，控制稳定性好，抗干扰能力强；缺点是：需要控制的变量较多，存在稳态误差。

1.3 复合张力控制系统

复合张力控制系统将直接张力控制和间接张力控制进行结合，通常做法是在间接张力的电流环和速度环基础上，再加入一个张力闭环，形成三闭环的控制。该系统的优点是：控制精度好，有良好的动态性能和跟随性能；缺点是：造价高，控制方式较为复杂，且存在一些缺陷，比如，初始建立张力时系统容易震荡等。

2 间接张力控制的策略分析

本系统中传动系统采用的是间接张力控制系统，即通过给定电机转矩限幅值来实现张力控制。在传动系统启停或变速时需考虑的主要问题是：如何解决因速度改变造成惯性转矩变化对张力的影响？在传动系统稳定时，要克服因卷径或其他参数变化而带来的张力波动。浙江某镀膜厂已采用了这种间接张力控制系统，系统的结构框图如图1所示，上位机用于监控整套系统的参数，包括传动参数和工艺参数；PLC用于实现卷径计算，静、动态补偿及其他工业参数的控制；PLC、S120伺服驱动器和伺服电机用于通信。

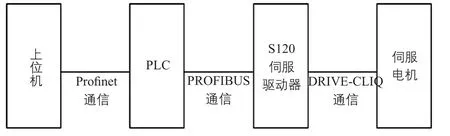
图1 系统结构框图

间接张力控制系统是以电流和速度控制器为核心的电流、速度双闭环串级控制系统，速度环为外环，电流环为内环。外环是通过速度给定和速度反馈来实现闭环，内环是通过速度环输出电流和对电流的监测来实现闭环。在间接张力控制过程中，首先使速度环输出饱和，速度控制器输出给定转矩限幅值，再附加变速过程中的惯性转矩和摩擦转矩，系统只有电流环起到调节作用，通过改变转矩设定输出来改变电流输出以完成张力控制[2]。

为保证在间接张力控制中达到设定的张力值，电动机的输出转矩需等于各部分阻力力矩之和。通过动态力矩平衡公式可得出它们的关系。

动态力矩平衡公式为：

式中，M为输出转矩，N·m；Mt为设定张力转矩，N·m；Mf为摩擦转矩，N·m；MJ为惯性转矩，N·m。

2.1 设定张力转矩

设定张力转矩是控制系统为满足铝带张力而提供的转矩设定值，即张力转矩的公式为：

式中，Ut为单位横截面积上的张力给定值；At为铝带的横截面面积；Dact为铝带卷的实时卷径。

由式(2)可知，Dact是影响Mt的主要因素，因此，获取Dact是十分重要的。此处计算Dact采用的是速度比计算法，根据给定速度辊的转速计算出整条生产线的线速度V，通过卷取电机的编码器得到电机转速n，i为电机和卷筒之间的齿轮比，根据卷取辊与整条生产线线速度相同原则就可以计算出当前的Dact值。采用速度比计算实时卷径的公式为：

这种测量方法会因带子的打滑而引起误差，因此在程序中做了卷径的校验，这样就保证了卷径的精确性。

2.2 摩擦转矩

系统运行时要克服摩擦力产生的摩擦转矩，摩擦转矩公式为：

式中，Bf(t)为阻尼系数；n(t)为滚筒的转速。

摩擦转矩在传动运行中一直都有，且在不同速度时摩擦转矩值的大小不同，需要进行分别补偿。S120伺服驱动器中有摩擦转矩的补偿功能[3]，速度不同时可获取不同的转矩值，最多能获得10组数据，其余数据可用线性插值的方法获得。

2.3 惯性转矩的转动惯量

图2 S120 摩擦特征曲线

在生产中，当传动系统的传动速度改变时，传动系统的输出转矩也应做相应改变，这部分用以适应速度变化的转矩称为惯性转矩。为了使铝带的张力稳定，必须对电机输出的转矩进行惯性补偿。将速度改变时产生的惯性转矩叠加至输出转矩上，这样能克服在传动变速时，由于惯性转矩波动而引起铝带过松或过紧，甚至断带的问题。电机速度的下降和卷筒上带材的质量增加会造成转动惯量的变化。电机转轴上的转动惯量包括两部分：一部分为固定惯量Jfix，它是卷筒、传动轴及减速机等转化到电动机转轴上的转动惯量；另一部分为可变惯量Jvar，它是铝卷的转动惯量，该惯量随着卷径的减小而减小。固定惯量和可变惯量之和就是总的转动惯量。

2.3.1 固定惯量Jfix

可由测试法得出卷取机的转动惯量，具体测试步骤如下：

1)卷取机空载时，转速给定为卷取电动机的额定转速ne，设定电机的加速时间为t1，电机从零开始加速，通过计算出电机的加速度，再将其转换为角加速度，同时录制加速过程中的转矩值Ma，并取其平均值。

2)录制电机达到额定转速时的转矩值Mb。

3)设定电机的减速时间，此处的减速时间和加速时间设置为相同的值，同时进行减速并录制减速过程中产生的转矩值Mc，并取其平均值。

空载运行中的受力分析：电机加速时驱动转矩除了要平衡Ma因惯性产生的制动转矩外，还要克服旋转轴系机械摩擦转矩。而摩擦转矩则为通过空载的匀速运行获得的Mb，因为此时系统加速度为零，所以动转矩为零，电机的驱动转矩与摩擦转矩平衡，所以系统摩擦转矩等于Mb。即：

式中，a为旋转角加速度。

同理，在电机的空载制动过程中，电机制动转矩加上系统摩擦转矩与惯性产生的制动转矩平衡，即：

式中，a′为旋转角减速度。

上文已提到a′=a，所以将式(5)与式(6)相加，即可将系统摩擦转矩消掉。这样做的目的就是尽量减少误差环节。即：

式(7)也可表示为：

其中：

2.3.2 可变惯量Jvar

卷取机上的铝卷可认为是一个空心圆柱体，它绕轴线的转动惯量可用空心圆柱体绕轴线的转动惯量公式来表示，即：

式中，ρ为铝带的密度；z为铝箔的卷紧系数；b为铝箔宽度；D0为收卷辊轴心直径；i为减速比。

2.3.3 总转动惯量Jtotal

综上所述，卷取机的总转动惯量Jtotal为：

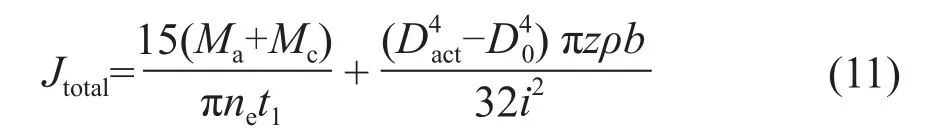
2.4 惯性转矩[4]

在收卷过程中，卷取机的卷径不断变大，卷筒的总转动惯量Jtotal也相应地增加，而卷取机的角速度w不断地降低，这就说明转动惯量和角速度均是时间t的函数，则卷筒上的惯性转矩MJ表示为：

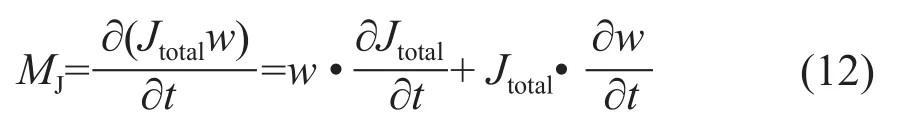
其中，可由式(13)求得，即：

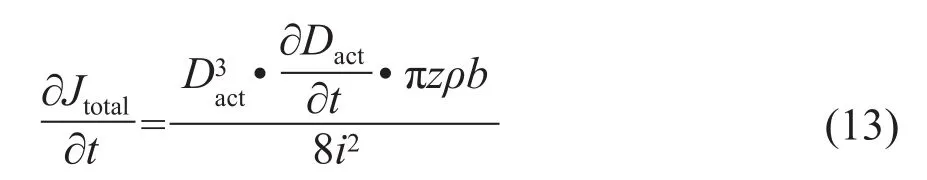
由于角速度w可由卷筒线速度V和卷径Dact表示，即：

由于线速度V和卷径Dact均是时间t的函数，因此对角速度w求偏导得到：

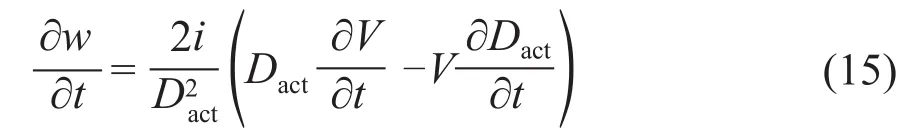
又因为卷筒每旋转一圈，卷径将增加2倍的铝带厚度h，因此有：

由上述推导最终可得到惯性转矩MJ为：

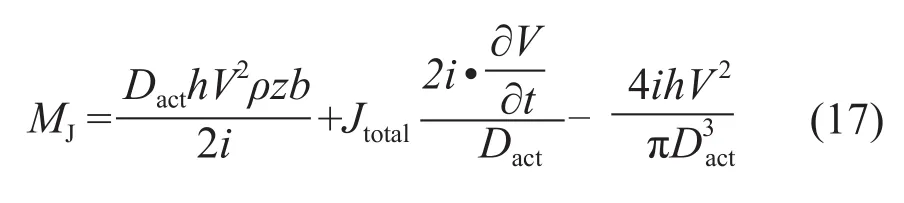
由式(17)可知，当铝带的型号确定好之后，影响惯性转矩的变量只有带材的线速度V、速度变化率和卷径Dact这3个变量。式(17)可由3个部分组成，第1部分中惯性转矩值同卷径值和线速度值成正比；第2部分为电机速度改变时所需的惯性转矩，当速度不变时该转矩为零，当卷取电机速度改变时该转矩不为零，为了使张力恒定，在转矩控制过程中要加上这部分转矩；第3部分为卷径改变时产生的惯性转矩的变化量。

2.5 小结

上文介绍了影响张力控制精度的设定转矩、摩擦转矩及惯性转矩等关键参数，并给出了如何获取这些参数的正确方法，可用以指导实际应用。

3 结论

根据铝带卷径变化大和系统稳定性要求高的特点，本文选用间接张力控制的方法，并给出了影响控制精度的关键参数的获取方法，该张力控制方法已应用在某厂的镀膜机上，根据伺服电机实际监测的转矩值和速度值，可以证明该卷取机张力控制取得良好的效果。又因为张力控制的精度高，所以带材速度波动小涂层的均匀性高，对于提高太阳能选择性吸收涂层的产品质量和生产效率都具有重要意义。

[1]王刚.基于Prof i bus的酸洗线卷取机张力控制系统设计[D].西安：西安科技大学, 2008.

[2]孙杰,李旭,谷德昊,等.高精确度铝箔张力控制策略的研究与应用[J].电机与控制学报, 2011, 15(12)： 74－77.

[3]Siemens. SINAMICS S120 2012 功能手册[Z].西门子, 2012-01.

[4]陈跃华.冷连轧卷取机恒张力控制技术[J].冶金自动化,2013, 37(1)： 35 － 37.