基于辐射条件的光伏系统容配比优化设计方法研究

中广核太阳能开发有限公司 ■ 牟娟 范忠瑶 易金印

0 引言

随着近年来国内光伏行业的发展日趋成熟，加之光伏政策倒逼机制，采用光伏电站系统精细化设计来推动电站成本下降已经成为市场的必然选择。优化光伏组件容量与逆变器容量的比值，即光伏-逆变器容配比，成为推动光伏电站全生命周期发电量提升和度电成本下降切实有效的途径之一。

目前光伏电站的光伏-逆变器容配比一般按照1：1设计，但根据电站光资源情况及实际运行状况分析，电站逆变器绝大部分时间都在小于额定功率的情况下运行，尤其在3类资源区更为突出，所以在一定程度上造成了资源的浪费。因此，在光伏电站系统优化设计中，适度提升光伏-逆变器容配比，有利于提升系统整体的经济效益。

光伏-逆变器容配比设计因地而异，不能仅凭经验方法，应更多考虑光伏组件的运行工况及当地气象条件才合理[1]。本文研究提出一种光伏系统容配比设计方法，建立组件在一定范围环境条件下的输出模型，根据Meteonorm软件数据库中的每10 min辐射值及温度，得出光伏阵列在一定范围环境条件下的实际输出功率，通过调整容配比计算弃光率，再考虑到系统的投资成本、运维成本、电价等因素，最后以系统投入/产出比最低为寻优目标得出某地的最佳光伏-逆变器容配比。

1 光伏-逆变器容配比设计方法研究

1.1 项目地多年代表辐射数据的选取

要确定某个项目地点的光伏-逆变器容配比，首先要了解当地一年四季每天的日辐射曲线，在此基础上才能计算逆变器的日输入/输出曲线，从而确定弃光率及最佳光伏-逆变器容配比。通过对比国内外各种辐射数据库，发现Meteonorm数据库中的辐射数据可以代表项目所在地未来多年的辐射情况。软件可以获得某地水平面和任一倾斜面上每min或每10 min的日均辐射数据，此数据来源于我国98个地面气象辐射观测站的20年均值。对于某一点的数据，根据较近的几个地面站的辐射数据，可采用插值法计算得出；对于距离地面站较远的地区，则采用卫星数据。

本文提出的光伏-逆变器容配比设计方法，采用Meteonorm 7.1.4版本中的每10 min倾斜面日辐射数据作为当地多年辐射数据的来源。

1.2 一定范围环境条件下逆变器侧实际输出功率的计算

组件超配设计时，逆变器在特定时间段会存在限功率运行，要计算这部分弃光率，需要先得出逆变器侧的实际输出功率。

此项计算分为两步：首先，计算出组件在一定范围环境条件下的实际输出功率；然后，确定组件输出至逆变器输出侧的效率。

1.2.1 组件工作温度的计算

光伏组件的输出功率与组件上的太阳辐照度及组件工作温度密切相关[2]。根据电站实际气象条件模拟组件的实际输出功率，是设计最佳光伏-逆变器容配比要重点解决的问题之一，而此问题的关键在于建立一定范围环境条件下组件工作温度的计算模型[3]。

基于正常工作温度条件(Nominal Operating Cell Temperature，NOCT)预测组件工作温度的方法被广泛应用于开放式支架系统[4]。一定范围环境条件下的组件实际工作温度Tc的计算公式为：

式中，Tair为环境温度，K；G为实际辐照度，W/m2；TcN为NOCT条件下的组件温度，K，取273+(45±2)；TaN为NOCT条件下的环境温度，K，取273+20；GTN为NOCT条件下组件表面的辐射量，W/m2，取800；η为组件转换效率；τβ为常数，一般取0.9[5]。

光伏组件的NOCT，即太阳辐照度为800 W/m2、环境温度为20 ℃、风速为1 m/s，无外部负荷，电池处于开路状态，电池片倾角与水平面成45°，支架结构为后背面打开状态。通常，NOCT的各参数值都可以直接从厂商提供的组件铭牌上得知。

光伏组件在实际运行时，根据所测得的现场实际太阳辐照度G和环境温度Tair，利用式(1)可计算得出组件的实际工作温度Tc。

1.2.2 组件输出功率的计算

一定范围环境条件下的组件实际输出功率P的计算公式为：

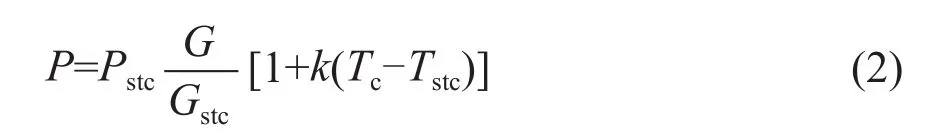
式中，Pstc为组件额定输出功率；Gstc为STC状态下的太阳辐照度，取1000 W/m2；Tstc为STC状态下的组件工作温度，取25 ℃；k为组件的功率温度系数。

根据式(2)，对于给定的组件，已知其STC状态下的太阳辐照度、工作温度和功率温度系数，可计算得出任意太阳辐照度和温度下的组件实际输出功率P。

1.2.3 逆变器侧实际输出功率的计算

在光伏系统中，从太阳辐射到光伏组件，再经汇流箱、直流电缆、直流配电到达逆变器及变压器的过程中，每个环节均存在损耗。但在本文光伏-逆变器容配比设计中，因为需要计算逆变器的实际输出功率来统计弃光率，所以需要确定逆变器之前的系统效率，如表1所示[6]。

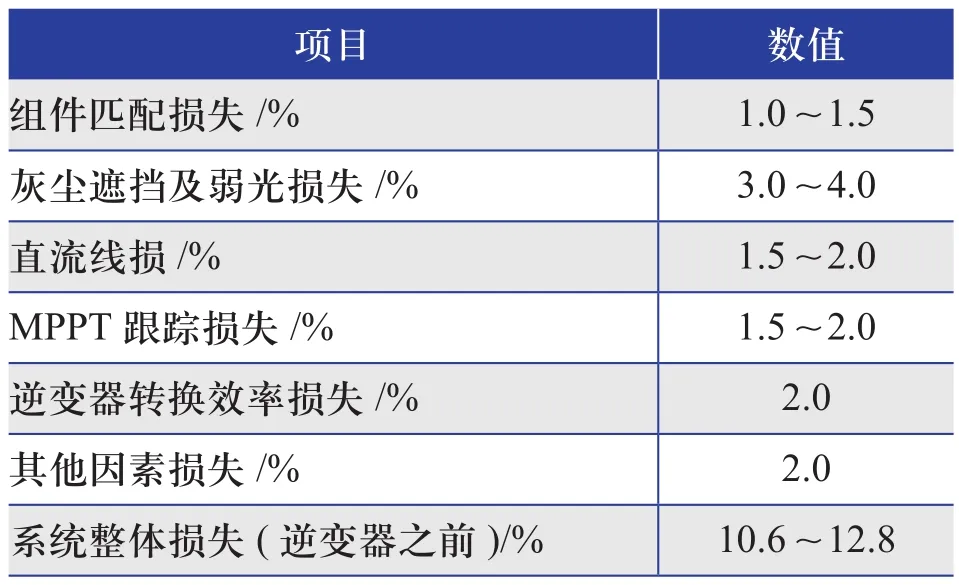
表1 系统效率示意图

容配比设计中，对于系统损耗的确定，可根据电站位置、系统技术方案、设备选型等情况合理确定，一般系统损耗约在10.6%～12.8%之间[7]。

根据上文的分析可知，通过输入某地实时的太阳辐照度和环境温度，考虑系统损耗，可计算出光伏阵列的实际输出功率；随着容配比的增大，组件容量的提高，逆变器的输出功率会高于额定功率，存在限光运行，根据逆变器的理论输出及实际输出，可计算得出每个容配比下的弃光率。

1.3 容配比优化目标的选定

投入/产出比(C/I Ratio)是指项目寿命期内的总成本与总收益的比值[8]，其计算公式为：

总成本包括系统初始投资、运行期总运维费用、总的财务费用及固定资产残值；总收益包括系统运行期的总发电收益，同时考虑折现率、弃光率及组件功率衰减的影响。投入/产出比RC/I在计算过程中几乎考虑了光伏电站整个寿命期的所有投入与产出，并考虑了资金的时间价值，适用于科技项目、技术改造项目和设备更新项目的技术经济评价指标；RC/I值越小，表明经济效果越好。

RC/I与内部收益率IRR的关系为[9]：

式中，nc为项目建设期，年；ng为项目运行期，年。在光伏项目中，一般nc=0.6，ng=25。

则式(4)可简化为：

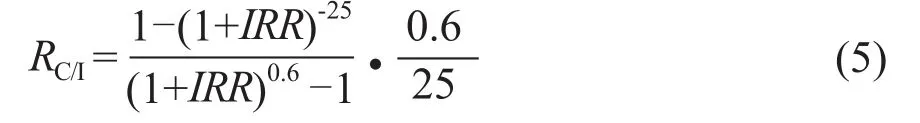
由式(5)可知，当项目的建设期和运行期确定后，RC/I与IRR存在一一对应的关系，如图1所示。

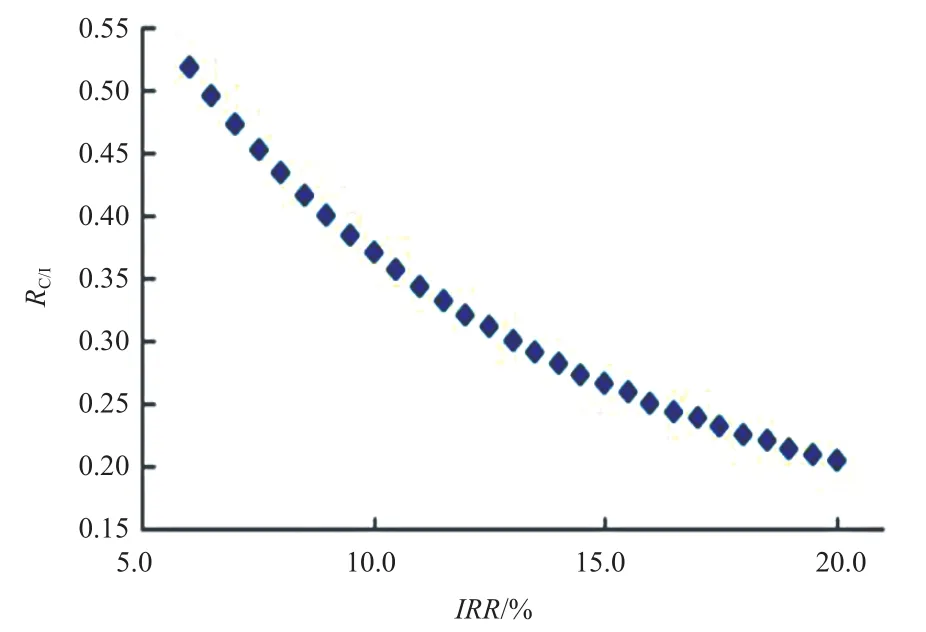
图1 R C/I与IRR的关系

与IRR相比，RC/I能更直观地表现项目的经济性和可行性；并且在项目建设期和运行期确定后，RC/I和IRR具有一一对应的关系，所以，本文选择RC/I作为容配比设计的寻优目标。

1.4 光伏-逆变器容配比优化设计的步骤

1)根据项目所在地的地址信息，利用Metenorm软件导出该地区每min或每10 min的倾斜面辐射数据和温度值。

2)根据式(1)、式(2)并结合系统效率，计算出组件在任意太阳辐照度、任意温度下的实际输出功率。

3)根据组件实际输出功率，结合系统效率分析结果，可计算出逆变器输出侧的实际输出功率。

4)设定逆变器输出功率范围，在组件超配设计时，逆变器可根据设定的功率范围限制功率输出，从而可计算出弃光率。

5)根据财务输入参数(投资、电价、贷款利率、折现率、运维成本等)，结合弃光率，计算得出每个容配比下的投入/产出比。

6)通过寻优不同容配比下投入/产出比最小值，实现光伏-逆变器容配比寻优。

2 3类资源区的算例容配比优化设计及经济效益分析

2.1 算例描述

在我国Ⅰ、Ⅱ、Ⅲ类光伏资源区内，各选择1个代表站点，按照上述计算方法分析当地的最佳光伏-逆变器容配比。

地点选择时需要重点考虑两方面：1)所选地点具有国家辐射监测站点，这样辐射数据来源会相对精确；2)所选地点在其所在资源区内具有一定代表性。

依据以上两点原则，共选择3个站点：Ⅰ类资源区选择玉树，Ⅱ类资源区选择北京，Ⅲ类资源区选择合肥，然后进行最佳容配比的算例设计。

2.2 算例的容配比优化设计

2.2.1 系统输入参数的确定

以1 MW光伏方阵为例，组件选择270 W多晶硅组件，系统总体投资按照7元/W计算；考虑目前的组件价格，组件每超装1 W，系统投资增加3.6元。组件功率衰减按照首年2.5 %，以后逐年0.7 %的比率计算；各项系统损耗(至逆变器直流侧)的取值如表2所示，在实际电站的优化设计中，要根据项目地点的实际情况和技术方案，合理确定各项系统损耗。本文结合实际算例，系统损耗取88.1 %。

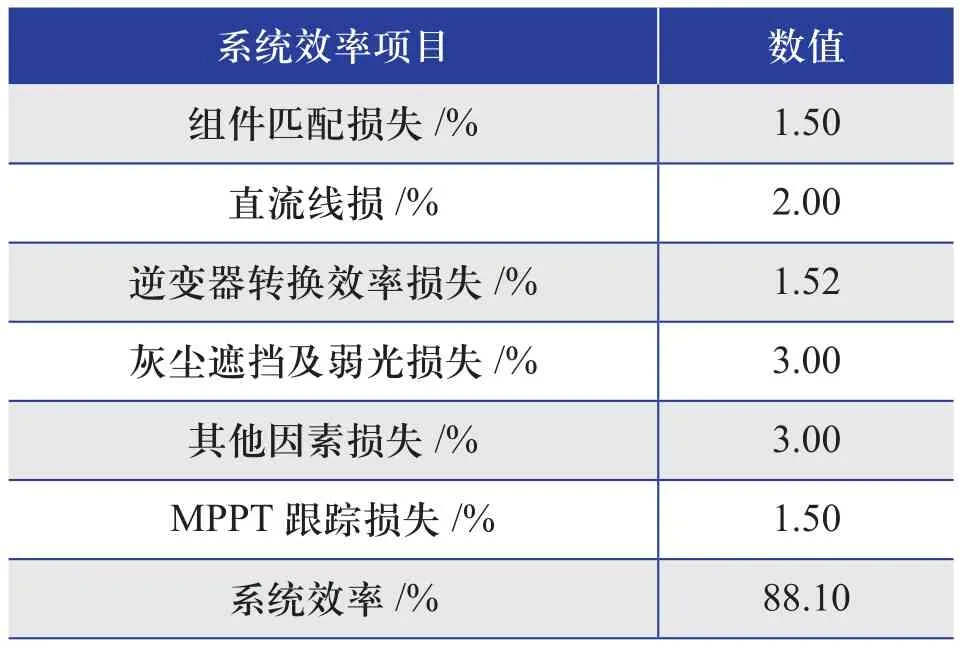
表2 系统效率的确定(至逆变器侧)

2.2.2 各资源区最佳容配比的确定

1)由Meteonorm软件导出一年中的每10 min辐射数据及温度值，辐射数据为1991～2010年20年的均值，包括水平面总辐射和某一倾角的倾斜面总辐射，其倾斜面上的辐射量计算模型采用perez模型[10]。

2)根据导出的辐射数据及温度值，利用式(1)和式(2)计算得出1 MW组件在实际环境中的实际输出功率，再根据88.1 %的系统效率计算得出逆变器的实际输出功率。

3)由于逆变器输出功率的限制，在增大组件配比时，逆变器输出功率会部分受限，从而计算得出弃光率。

4)输入财务指标参数，计算每个容配比下的投入/产出比。财务指标中，固定资产残值按照总投资的5%取值，总投资中70%来自银行贷款，运维成本按照120元/(kW·a)计算，不同资源区的电价、土地费用不同。各项边界条件如表3所示。3个地区不同容配比下的投入/产出比如表4及图2所示。

由图2可知，Ⅰ类资源区的玉树地区的最佳容配比为1.2：1，Ⅱ类资源区的北京地区的最佳容配比为1.45：1，Ⅲ类资源区的合肥地区的最佳容配比为 1.6：1。

为更直观说明逆变器对输出功率的限制所导致的部分弃光，各选择3个地区的一天逆变器限功率输出曲线，如图3所示。

表3 3个地区的各项边界条件

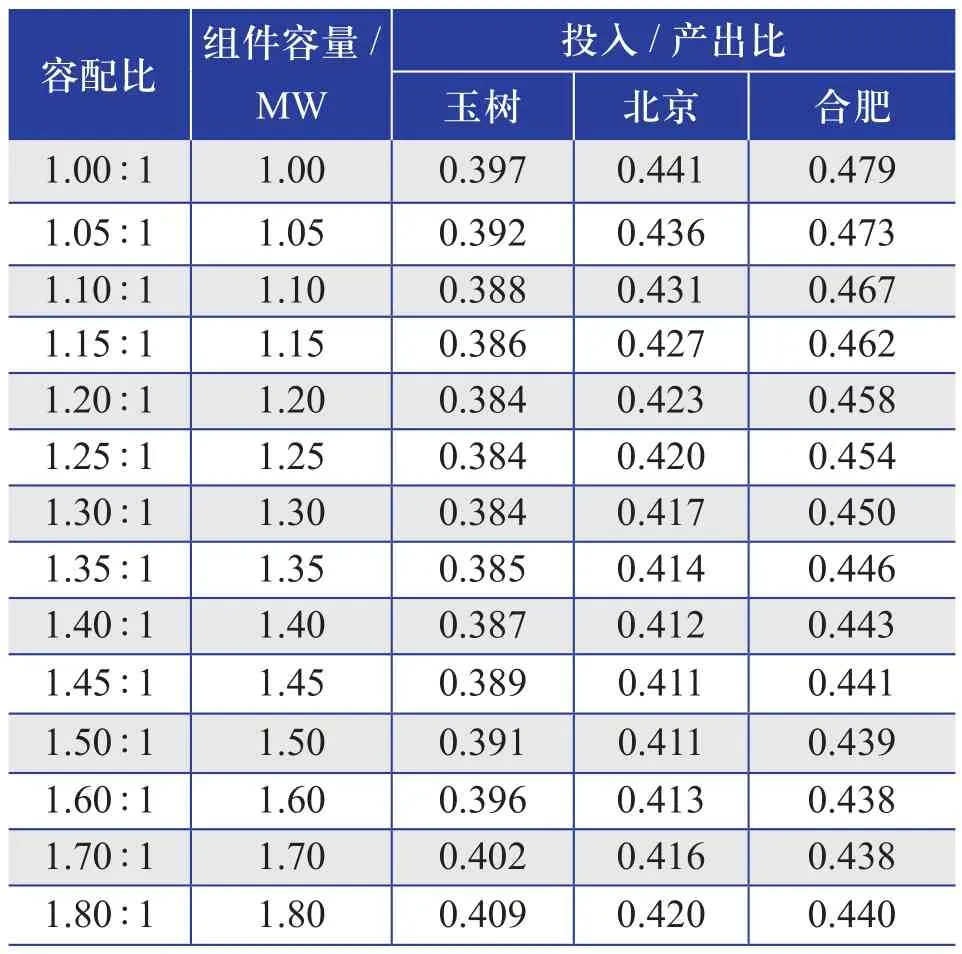
表4 3个地区在不同容配比下的投入/产出比

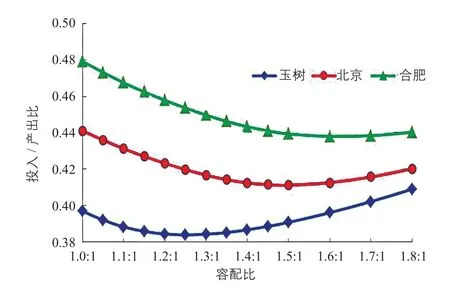
图2 3个地区在不同容配比下的投入/产出比折线图

图3 3个地区的全天限功率输出曲线

2.3 优化设计前后算例经济效益分析

以玉树地区为例，计算在最佳容配比设计下的电站经济效益提升。以10 MW光伏电站为例，玉树地区首年满负荷小时数为1539 h，暂不考虑电网限电，资本金出资比例为30%，系统造价按照7元/W计算，在容配比为1：1时，计算得出全投资内部收益率IRR为11.71%，投资回收期为7.43年。

在最佳容配比1.2：1下，考虑到组件成本和土地费用的增加，系统投资增长为7.724元/W[11]，运维成本和财务费用也有相应提高；但由于组件容量的增加，会存在自动弃光，经计算，首年弃光率为1.66%。10 MW光伏电站系统初始投资增加724万元，但每年发电量增加收入221万元，计算得出全投资内部收益率IRR为12.71%，投资回收期为6.5年。

两种容配比下的财务指标比较如表5所示。

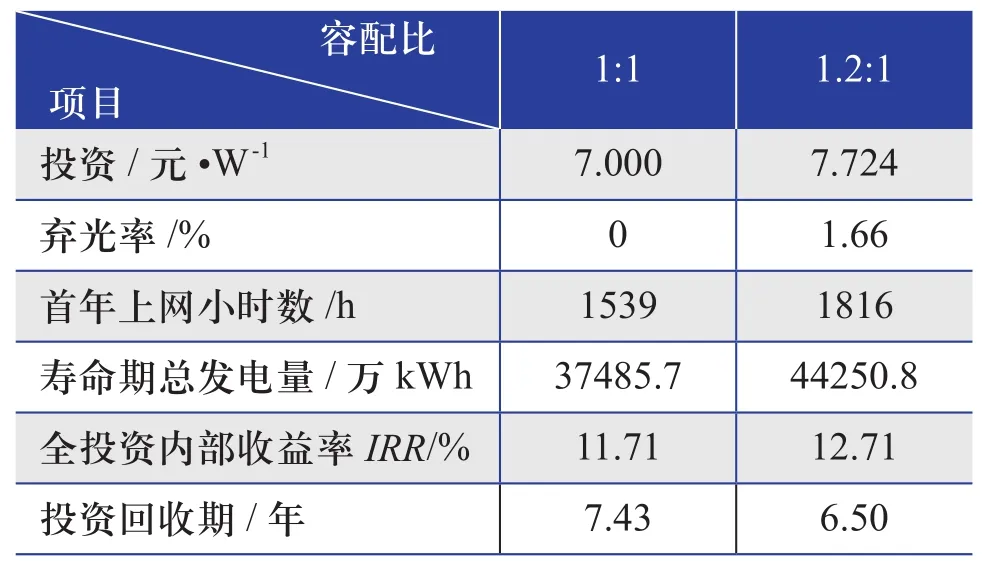
表5 最佳容配比与传统容配比财务指标比较

3 结语

本文提出了一种光伏电站最佳容配比的设计方法：首先建立组件功率输出模型；其次利用Meteonorm数据库中的辐射数据及温度值，确定逆变器交流侧输出曲线，并计算弃光率；通过以投入/产出比最低为寻优目标，寻找当地最佳的容配比。文中利用此方法分别验证计算了3类资源区3个项目地点的最佳容配比，并以玉树为例，分析了在最佳容配比设计下电站的增量经济效益，得出结论如下：

1)本文提出的容配比设计方法可用于具体工程优化设计。

2)计算电站投入/产出比时，要综合考虑项目所在地点的土地费用、运维成本及因超配带来的弃光损失，指标因地而异，指标的选取是否合理将直接影响到结果的准确度。

3)在最佳容配比下分析财务指标可知，从静态指标来看，3～4年增加的收益即可弥补初始投资的增加；从动态指标来看，采用最佳容配比可将项目IRR提高至少1%，并缩短投资回收期。

4)由于项目每10 min的辐射数据来自于Meteonorm数据库，而此数据库只能提供固定某一角度倾斜面上的辐射量，所以本文所述容配比设计方法仅适用于采用固定倾角安装的系统。

[1]王隆联, 唐彬伟. 基于运行工况的光伏容量优化配比算法分析[J]. 电器与能效管理技术, 2016, (7)： 26－29.

[2]恽旻, 孙晓, 周滢, 等. 辐照度和温度对光伏组件光电转换性能测量的影响[J]. 现代测量与实验室管理, 2015, (4)： 3－5.

[3]谢丹，鞠健, 于苗苗, 等. 光伏电池阵列布置模式的探讨[J].太阳能 , 2013, (23)： 28－31.

[4]Davis M W, Fanney A H, Dougherty B P. Prediction of Building Integrated Photovoltaic Cell Temperatures[J]. Journal of solar energy engineering, 2001, 123(3)： 200 － 210.

[5]Duffie J A, Beckman W A, Mcgowan J. Solar engineering of thermal processes[J]. A Wiley-Interscience Publication, 1980, 116(1)： 549.

[6]刘国忠, 范忠瑶, 牟娟, 等. 不同安装倾角对光伏电站发电量的影响研究[J]. 太阳能学报, 2015, 36(12)： 2973－2977.

[7]陈详. 光伏电站发电量的理论计算及差异分析[J]. 太阳能,2011, (1)： 39 － 40.

[8]王斯成. 如何提高光伏电站的效益[A]. 光伏精细化设计论坛[C]. 呼和浩特, 2016-07.

[9]刘朋杰. 一种新的项目评价指标[J]. 东北电力大学学报,2002, 22(3)： 53 － 55.

[10]牟娟. 几种倾斜面辐射量计算模型的对比分析[J]. 太阳能,2013, (23)： 50 － 51.

[11]牟娟. 光伏电站可调式支架经济效益分析[J]. 可再生能源,2013, 31(6)： 23 － 25.