简谐运动的解读
■河北省鸡泽县第一中学 高志彬
一、简谐运动的五个特征
1.动力学特征:F=-kx,“-”表示回复力的方向与位移方向相反,k是比例系数,不一定是弹簧的劲度系数。
2.运动学特征:物体做简谐运动的加速度与物体偏离平衡位置的位移成正比,且二者的方向相反,物体做的是变加速运动,远离平衡位置时,位移、回复力大小、加速度大小、势能均增大,速度大小、动能均减小,靠近平衡位置时则相反。
3.运动的周期性特征:相隔nT(n=1,2,3,…)的两个时刻,振子处于同一位置且振动状态相同。
4.对称性特征:
(1)相隔(n=0,1,2,…)的两个时刻,振子的位置关于平衡位置对称,位移、速度、加速度大小相等,方向相反。
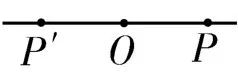
图1
(2)如图1所示,振子经过关于平衡位置O对称的两点P、P'(OP=OP')时,速度的大小、动能、势能相等,相对于平衡位置的位移大小相等。
(3)振子由P点到O点所用时间等于由O点到P'点所用时间,即tPO=tOP'。
(4)振子在往复运动过程中通过同一段路程(如OP段)所用时间相等,即tOP=tPO。
5.能量特征:振动的能量包括动能Ek和势能Ep,在简谐运动过程中,系统的动能与势能相互转化,系统的机械能守恒。
例1一弹簧振子沿x轴振动,平衡位置在坐标原点。t=0时刻,振子的位移x=-0.1m;t=s时刻,振子的位移x=0.1m;t=4s时刻,振子的位移x=0.1m。该振子的振幅和周期可能为( )。
A.0.1m,s B.0.1m,8s
C.0.2m,s D.0.2m,8s
解析:若振子的振幅为0.1m,s=,则振动周期的最大值为s,选项A正确,B错误。若振子的振幅为0.2m,由简谐运动的对称性可知,当振子由x=-0.1m处运动到负向最大位移处再反向运动到x=0.1m处,再经n个振动周期时所需总时间为s,则,所以振动周期的最大值为s,且t=4s时刻振子的位移x=0.1m,故选项C正确。若振子的振幅为0.2m,当振子由x=-0.1m经平衡位置运动到x=0.1m处,再经n个振动周期时所需总时间为s,则s,所以振动周期的最大值为8s,且t=4s时刻,振子的位移x=0.1m,故选项D正确。答案为ACD。
规律总结:(1)分析简谐运动中各物理量的变化情况时,一定要以位移为桥梁,当位移增大时,振子的回复力、加速度、势能均增大,速度、动能均减小;反之,则发生相反的变化。另外,各矢量均在其值为零时改变方向。(2)分析简谐运动的过程中要特别注意周期性和对称性。
二、简谐运动的图像
1.对简谐运动图像的认识:简谐运动的图像是一条正弦或余弦曲线,如图2所示。这个图像反映的是位移随时间的变化规律,图像随时间的增加而延伸,图像不代表质点运动的轨迹。
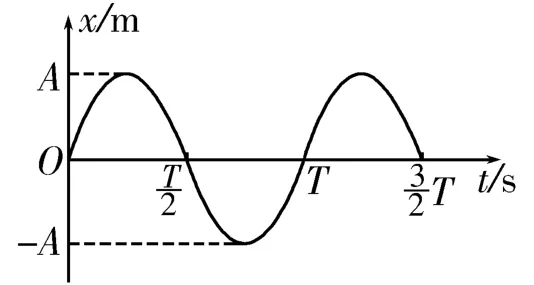
图2
2.图像信息:
(1)由图像可以得出质点做简谐运动的振幅、周期和频率。
(2)由图像可以确定某时刻质点离开平衡位置的位移。
(3)由图像可以确定某时刻质点的回复力、加速度的方向,因为回复力总是指向平衡位置,所以回复力和加速度在图像上总是指向t轴。
(4)确定某时刻质点速度的方向可以通过图像上质点在下一时刻位移的变化来判定。如果质点在下一时刻的位移增大,那么振动质点的速度方向就沿远离t轴方向;如果质点在下一时刻的位移减小,那么振动质点的速度方向就沿指向t轴方向。
(5)由图像可以比较不同时刻回复力、加速度的大小。
(6)由图像可以比较不同时刻质点的动能、势能的大小。
例2一质点做简谐运动,其位移和时间的关系如图3所示。
(1)求t=0.25×10-2s时质点的位移。
(2)在1.5×10-2s~2×10-2s时间内的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?
(3)在0~8.5×10-2s时间内,质点的路程、位移各多大?
解析:(1)由质点的位移—时间图像知振幅A=2cm,周期T=2×10-2s,简谐运动的表达式为x=Asin(ωt-)=-Acosωt=-2costcm=-2cos100πtcm。当t=0.25×10-2s时,x=-2coscm=cm。
(2)由质点的位移—时间图像可知,在1.5×10-2s~2×10-2s时间内的振动过程中,质点的位移变大,回复力变大,速度变小,动能变小,势能变大。
(3)在0~8.5×10-2s时间内经历个周期,质点通过的路程s=17A=34cm,质点的位移为2cm。
跟踪训练
1.某质点做简谐运动,其位移随时间变化的关系式为x=Asint,则( )。
A.第1s末与第3s末质点的位移相同
B.第1s末与第3s末质点的速度相同
C.第3s末至第5s末质点的位移方向都相同
D.第3s末至第5s末质点的速度方向都相同
2.一质点做简谐运动的位移—时间图像如图4所示,下列说法正确的是( )。
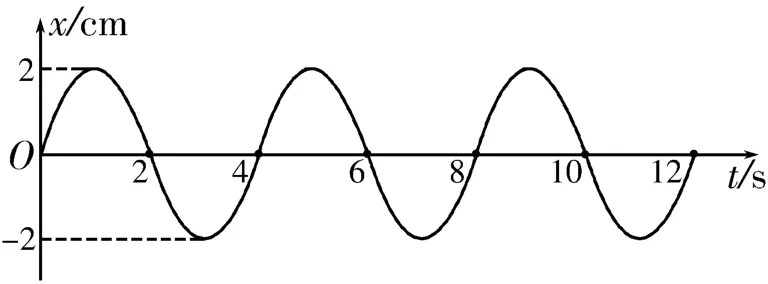
图4
A.质点的振动频率是4Hz
B.在0~10s时间内,质点经过的路程是20cm
C.第4s末质点的速度为零
D.在t=1s和t=3s两时刻,质点的位移大小相等,方向相同
参考答案:1.AD 2.B

