气体实验定律的两类模型问题剖析

■湖南省汨罗市一中 蒋 纬

气体实验定律的两类模型：(1)玻璃管液封模型;(2)汽缸活塞模型。这部分知识属于物理选修3—3模块，在高考中出题的概率为100%，且通常以计算题的形式出现。

一、玻璃管液封模型

例1如图1所示，一细U型管两端开口，用两段水银柱封闭了一段空气柱在管的底部，初始状态时气体温度为280K，图中封闭空气柱的长度L1=20cm，其余部分的长度分别为L2=15cm，L3=10cm，h1=4cm，h2=20cm。现使气体温度缓慢升高，取大气压强p0=76cmHg，求：

(1)气体温度升高到多少时右侧水银柱刚好全部进入竖直管?

(2)气体温度升高到多少时右侧水银柱与管口相平?

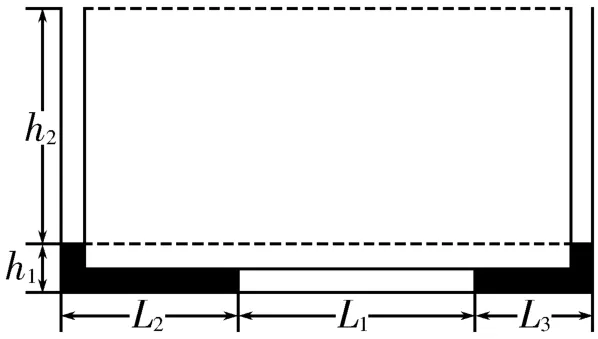
图1

解析：(1)设U型管的横截面积是S，以封闭气体为研究对象，初状态时的状态参量分别是p1=(76+4)cmHg=80cmHg，V1=L1S=20S。当右侧的水银柱全部进入竖直管时，水银柱的高度h=h1+L3=(4+10)cm=14cm，此时左侧竖直管中的水银柱也是14cm。气体的状态参量p2=(76+14)cmHg=90cmHg，V2=L1S+2L3S=40S。由理想气体的状态方程得，解得T2=630K。

(2)右侧水银柱全部进入右管后，产生的压强不再增大，所以左侧的水银柱保持不动，当右侧水银柱与管口相平时，气体的体积V3=L1S+L3S+h2S=50S，由盖-吕萨克定律得，解得T=787.5K。3

模型解读：求液柱封闭的气体压强时，一般以液柱为研究对象进行受力分析、列平衡方程。另外，需要注意以下四个问题。(1)液体因重力产生的压强大小p=ρgh(其中h为液柱的竖直高度);(2)不要漏掉大气压强，同时又要尽可能平衡掉某些大气的压力;(3)有时可直接应用连通器原理——连通器内静止的同种液体在同一水平面上各处的压强相等;(4)当液体为水银时，可灵活应用压强单位“cmHg”等，使计算简捷。

二、汽缸活塞模型

1.单一汽缸活塞模型的求解。

例2如图2所示，两端开口的汽缸水平固定，A、B是两个厚度不计的活塞，可在汽缸内无摩擦滑动，其横截面积分别为S1=20cm2，S2=10cm2，它们之间用一根细杆连接，活塞B通过水平细绳绕过光滑的定滑轮与质量M=2kg的重物C相连。活塞静止时汽缸中的气体温度T1=600K，汽缸两部分的气柱长度均为L。已知大气压强p0=1×105Pa，取g=10m/s2，缸内气体可视为理想气体。

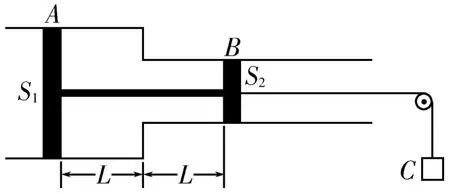
图2

(1)活塞静止时，求汽缸内气体的压强。

(2)若降低汽缸内气体的温度，当活塞A缓慢向右移动时，求汽缸内气体的温度。

解析：(1)设活塞静止时汽缸内气体的压强为p1，依活塞受力平衡得p1S1+p0S2=p0S1+p1S2+Mg，解得p1=1.2×105Pa。

(2)活塞A缓慢移动表明活塞受力平衡，因此汽缸内气体的压强保持不变。设初状态气体的温度为T1，末状态气体的温度为T2，由盖-吕萨克定律得解得T2=500K。

模型解读：求解汽缸活塞类问题往往需要综合考虑气体、汽缸或活塞等多个研究对象，灵活应用热学、力学等物理知识。另外，需要注意以下四个问题。(1)研究对象分两类，一类是热学研究对象(一定质量的理想气体)，另一类是力学研究对象(汽缸、活塞或某系统)。(2)对热学研究对象分析清楚初、末状态及状态变化过程，依气体实验定律列出方程;对力学研究对象要正确地进行受力分析，依力学规律列出方程。(3)注意挖掘题目的隐含条件，如关键字句包含的信息、几何关系等，列出辅助方程。(4)多个方程联立求解时，对得到的结果还需检验它们的合理性。

2.多系统问题的处理技巧。

例3如图3所示，两汽缸A、B粗细均匀，等高且内壁光滑，其下部由体积可忽略的细管连通。汽缸A的直径是B的2倍，汽缸A上端封闭，汽缸B上端与大气连通;两汽缸除A顶部导热外，其余部分均绝热，两汽缸中各有一厚度可忽略的绝热轻活塞a、b，活塞下方充有氮气，活塞a上方充有氧气。当大气压为p0、外界和汽缸内气体温度均为7℃且平衡时，活塞a离汽缸顶部的距离是汽缸高度的，活塞b在汽缸正中间。

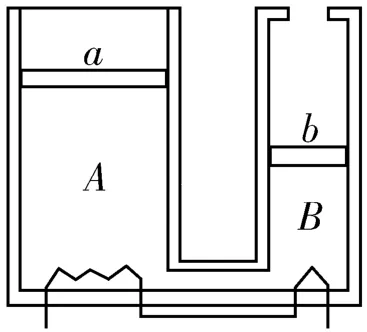
图3

(1)现通过电阻丝缓慢加热氮气，当活塞b恰好升至汽缸顶部时，求氮气的温度。

(2)继续缓慢加热，使活塞a上升，当活塞a上升的距离是汽缸高度的时，求氧气的压强。

解析：(1)活塞b升至汽缸顶部的过程中，活塞a不动，活塞a、b下方的氮气经历等压变化。设汽缸A的容积为V0，氮气初状态的体积为V1，温度T1=(273+7)K，末状态的体积为V2，温度为T2，则汽缸B的容积为由盖-吕萨克定律得，解得T2=320K。

(2)活塞b升至汽缸顶部后，由于继续缓慢加热，活塞a开始向上移动，直至活塞a上升的距离是汽缸高度的时，活塞a上方的氧气经历等温变化。设氧气初状态的体积为V1'，压强为p1'，末状态体积为V2'，压强为p'2，则V'1=V0，p'1=p0，V'2=V0。由玻意耳定律得p1'V1'=p2'V2'，解得p2'=

技巧解读：求解两个或多个汽缸封闭着几部分气体的多个系统问题时，往往以压强为桥梁建立起各系统间的关系，需要对各系统独立进行状态分析，还要确定每个研究对象的变化性质，分别应用相应的实验定律，并充分应用各研究对象之间的压强、体积、温度等量的有效关联。若活塞可自由移动，一般根据活塞平衡确定两部分气体的压强关系。

跟踪训练

1.如图4所示，在长度l=57cm的一端封闭、另一端开口向上的竖直玻璃管内，用4cm高的水银柱封闭着51cm长的理想气体，管内外气体的温度均为33℃，大气压强p0=76cmHg。现将水银徐徐注入管中，直到水银面与管口相平，此时管中气体的压强为多少?接着缓慢对玻璃管加热升温至多少时，玻璃管中刚好只剩下4cm高的水银柱?

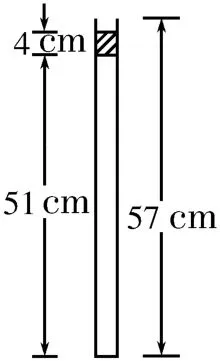
图4

2.如图5所示，一固定的竖直汽缸由一大一小两个同轴圆筒组成，两圆筒中各有一个活塞。已知大活塞的质量m1=2.5kg，横截面积S1=80cm2;小活塞的质量m2=1.5kg，横截面积S2=40cm2;两活塞用刚性轻杆连接，间距保持l=40cm;汽缸外大气的压强p=1×105Pa，温度T=303K。初始状态时大活塞与大圆筒底部相距，两活塞间封闭气体的温度T1= 495K。现汽缸内气体温度缓慢下降，活塞缓慢下移。忽略两活塞与汽缸壁之间的摩擦，取重力加速度g=10m/s2。求：

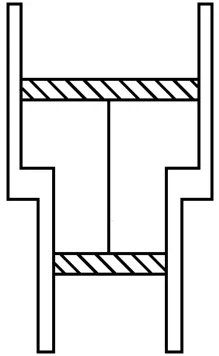
图5

(1)在大活塞与大圆筒底部接触前的瞬间，汽缸内封闭气体的温度。

(2)汽缸内封闭的气体与汽缸外大气达到热平衡时，汽缸内封闭气体的压强。

3.一U形玻璃管竖直放置，左端开口，右端封闭，左侧管内上部有一光滑的轻活塞。初始时，管内汞柱及空气柱长度如图6所示。用力向下缓慢推活塞，直至管内两边汞柱高度相等时为止。求此时右侧管内气体的压强和活塞向下移动的距离。已知玻璃管的横截面积处处相同;在活塞向下移动的过程中，没有发生气体泄漏;大气压强p0=75.0cmHg，环境温度不变。(保留三位有效数字)

图6

参考答案：

1.p2=85cmHg，T=318K。

2.(1)330K，(2)1.01×105Pa。

3.144cmHg，9.42cm。