时间序列分析法在北京市食物中毒预测中的应用

马晓晨 牛彦麟 吴阳博 王超 王同瑜 马蕊

食源性疾病是全球重点关注的公共卫生问题，造成严重的疾病负担。食物中毒是常见的食源性疾病，影响我国食品安全的主要问题，对其发病趋势进行早期预警、预测，为食物中毒控制工作提供参考依据，从而最大程度降低决策的盲目性。食物中毒的发生具有长期趋势、季节性、短期波动和不规则变动等特点。时间序列分析是运用历史的观点，根据系统有限长度的动态数据，分析序列的基本趋势、拟合理论模型并用于预测序列的未来发展趋势[1]。ARIMA模型是复合的季节模型，适合一些有季节变化的时间序列。现通过运用ARIMA模型对2004-2016年北京市13年食物中毒数据进行时间序列分析并建立预测模型，探讨通过ARIMA模型进行食物中毒发病情况预测的可行性，为预防和控制食源性疾病提供依据。

1 资料与方法

1.1资料来源 2004-2010年食物中毒发病人数数据来源于北京市卫生监督所历年食物中毒报表，2011-2016年食物中毒发病人数来源于北京市食源性疾病暴发监测系统。

1.2食物中毒的判定标准 食物中毒所有事件均经过流行病学调查，食物中毒的确定符合GB14938-94《食物中毒诊断标准及技术处理总则》的技术要求。

1.3研究方法 ARIMA预测模型，ARIMA(p，d，q)(P，D，Q)s，其中p和q为自回归和移动平均阶数，d为差分次数，P和Q为季节性自回归和移动平均阶数，D为季节性差分次数，s为季节周期。ARIMA模型建模的4个基本步骤：(1)序列平稳化。要求原始序列平稳，均数和方差不随时间变化;(2)模型识别。根据时序图和自相关图(ACF)和偏自相关图(PACF)，分析时间序列的随机性、平稳性和季节性，选择一个模型来拟合数据;(3)参数估计和模型诊断。通过拟合优度检验得到统计量对数似然函数、贝叶斯信息准则(BIC)等并进行假设检验，要求残差为白噪声;(4)模型预测。以2004-2015年各季度食物中毒发病人数拟合模型，利用2016年各季度发病人数和事件数检验模型预测效果，根据预测值得到95%置信区间，计算预测值与实际值的相对误差，以判断模型的预测精度，并进一步预测2017年食物中毒发病人数。

1．4统计学方法 采用SPSS 20.0建立2004-2016年各季度食物中毒发病人数数据库，并利用时间序列分析模块进行数据处理与分析。

2 结果

2．1序列平稳化 将北京市2004-2015年食物中毒的发病人数分别绘制序列图(图1)。由图1可知，北京市食物中毒发病人数呈明显的非平稳性和周期性。食物中毒发病人数呈明显的季节波动，第3季度出现中毒高峰，第1季度表现为低谷期。对食物中毒发病人数经自然对数转换、一次季节性差分后，基本消除了趋势性和季节性的影响，满足时间序列分析对于平稳性的要求(图2)。

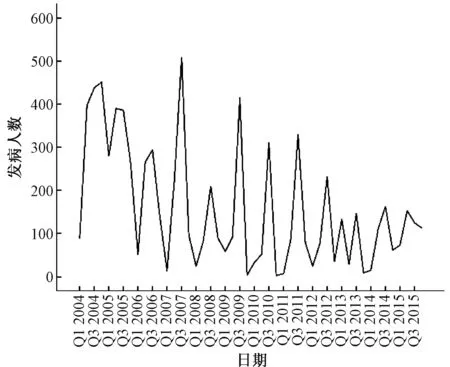
注：Q1为第1季度，Q3为第3季度。图1 北京市2004-2015年食物中毒季度发病人数时间序列图

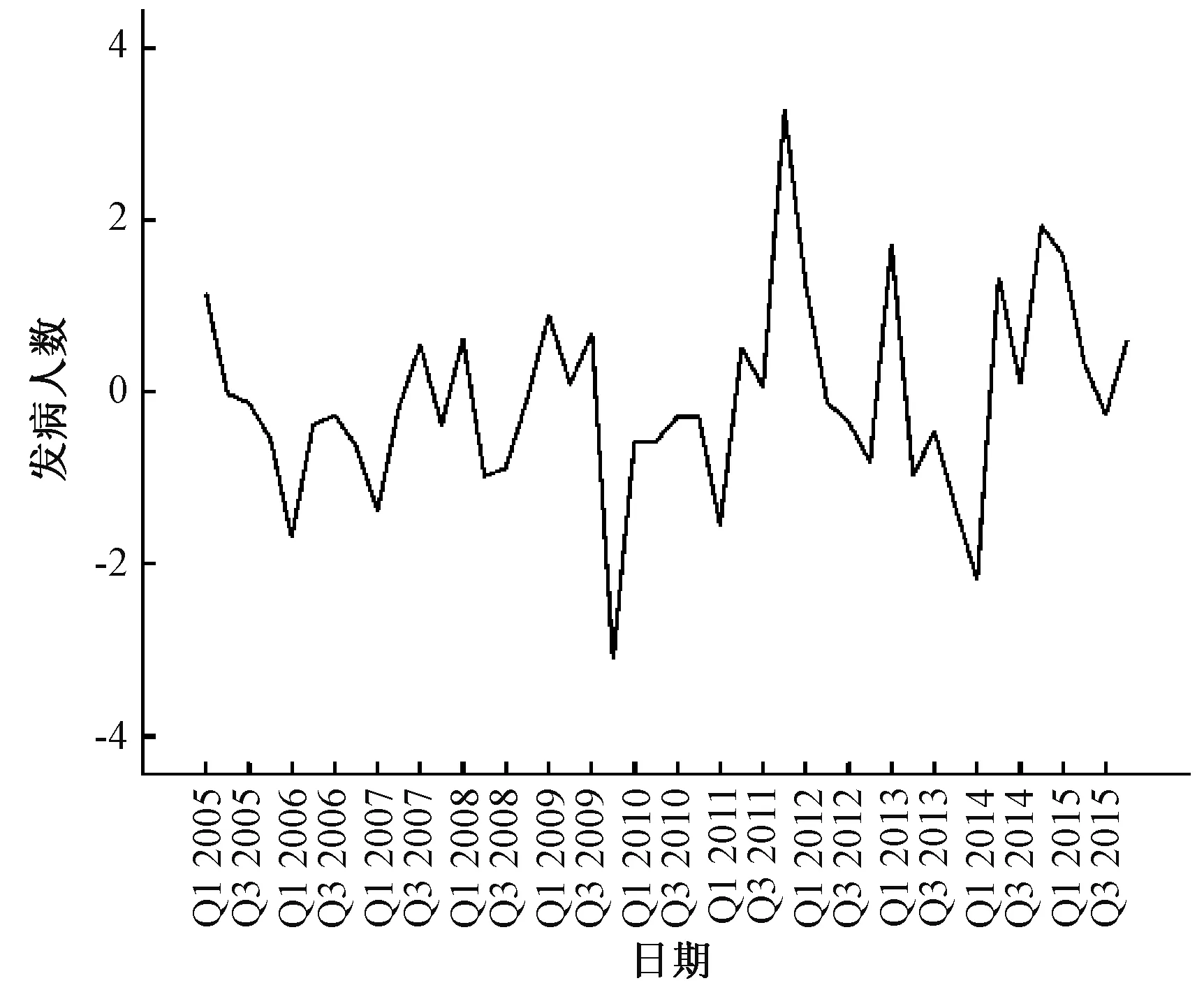
注：Q1为第1季度，Q3为第3季度。图2 经过自然对数和一阶季节差分后的食物中毒季度发病人数时间序列图

2．2模型的识别 经自然对数和一阶季节差分后可得到较为平稳序列，可初步估计食物中毒人数满足ARIMA(p，0，q)×(P，1，Q)4模型，4表示以4个季度为周期。根据ACF(图3)与PACF(图4)表明可初步选择p=1，q=0，ARIMA(1，0，0)×(P，1，Q)4。

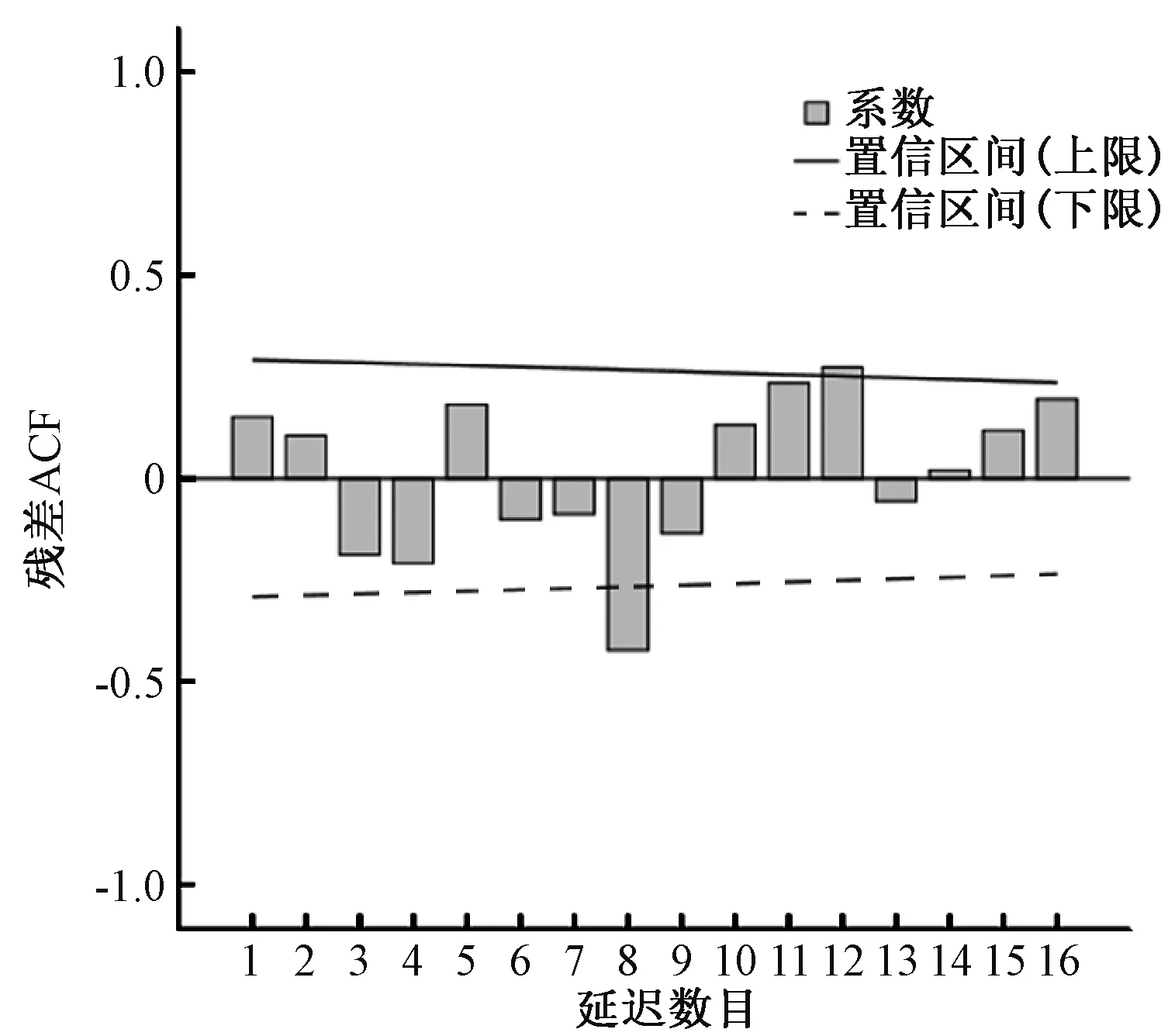
图3 经自然对数转换、一阶季节差分后的偏自相关图

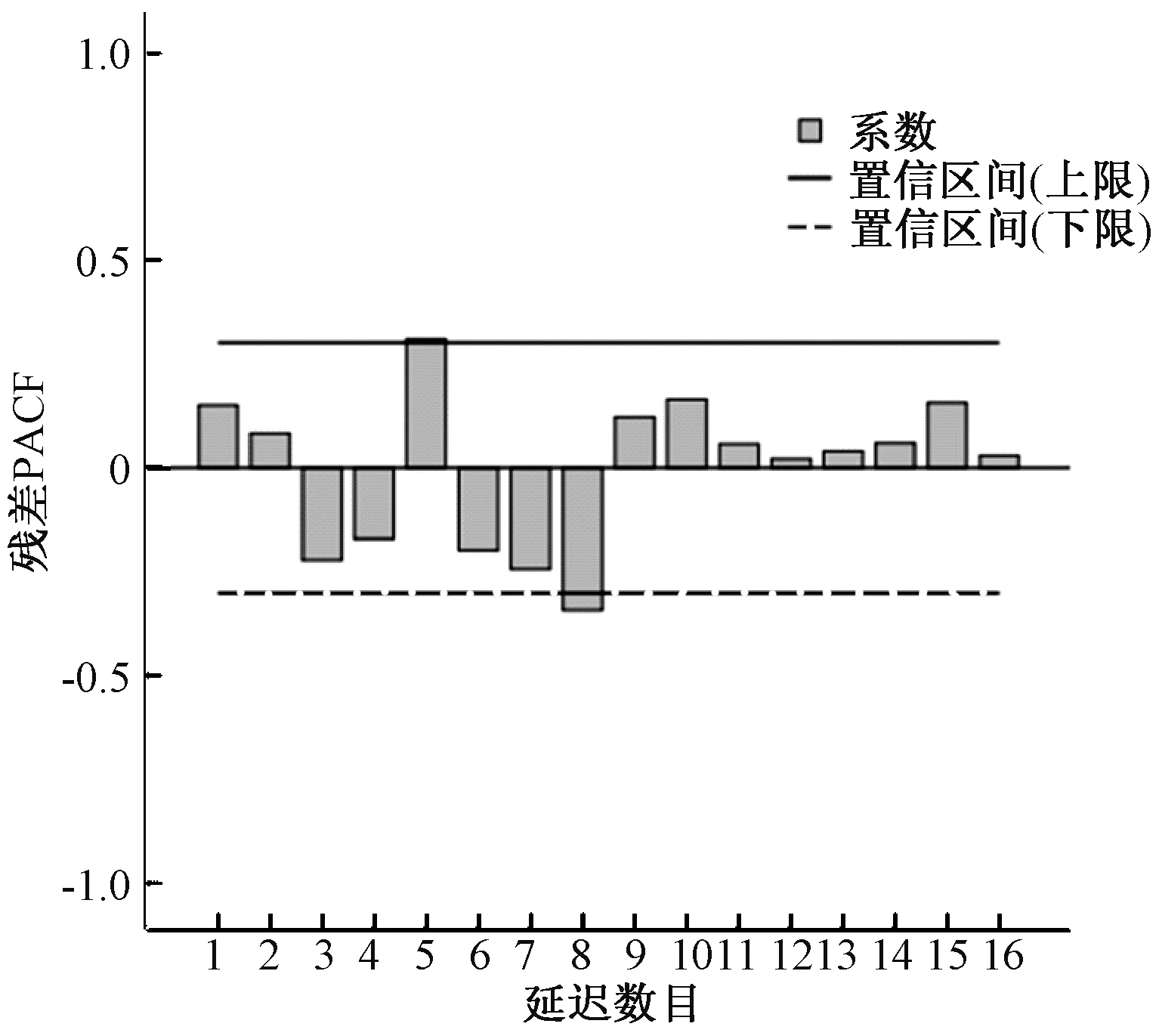
图4 经自然对数转换、一阶季节差分后的偏自相关图

2．3参数估计与模型诊断 对模型进行参数估计，SPSS 20.0自动对模型进行选择，食物中毒发病人数的模型为ARIMA(1，0，0)×(1，1，0)4为最优模型；通过运算标准BIC为9.263，调整R2为0.533，经检验模型参数经统计学检验得到P<0.05，具有统计学意义。残差的ACF图和PACF图(图5)显示残差的ACF和PACF均在置信区间内，且残差序列Ljung-Box检验统计量Q=17.03，P=0.383，差异无统计学意义，说明残差序列为白噪声，建立的模型恰当。

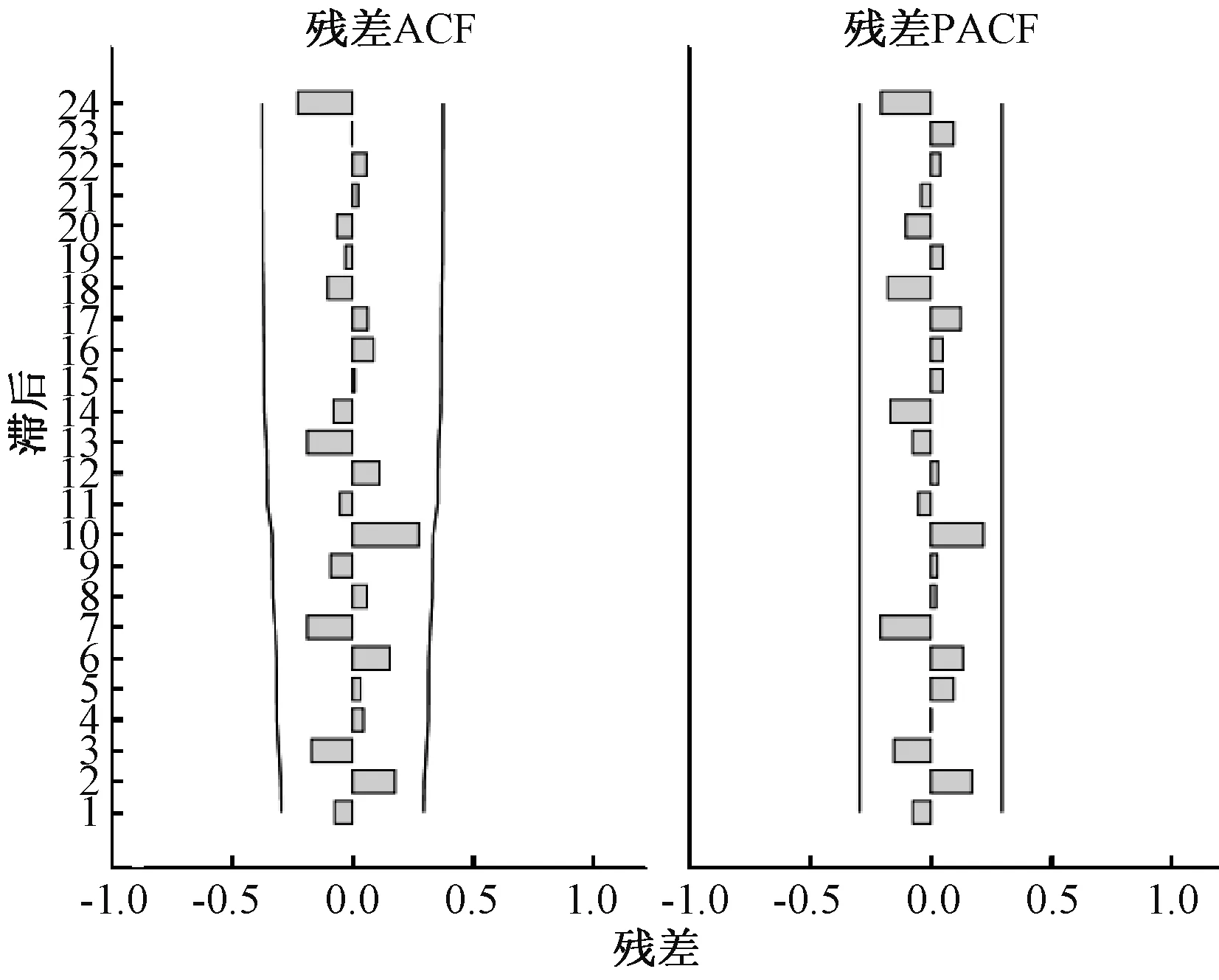
图5 模型ARIMA(1，0，0)×(1，1，0)4残差序列的ACF、PACF图

2．4模型预测 利用所建立的ARIMA(1，0，0)×(1，1，0)4模型，对2004-2015年北京市食物中毒发生人数进行拟合，对2016年北京市食物中毒发生人数进行预测，通过预测值与实际值的比较来验证模型，同时对2017年北京市食物中毒生人数进行预测。结果显示拟合值和实际值相比，虽然存在一定的差异性，但实际值均在拟合值的95%CI范围内(图6)。如表1所示，2016年的食物中毒人数预测值与实际值比较，得到平均相对误差率为6%。预测2017年北京市食物中毒的发生人数为264人(表2)。

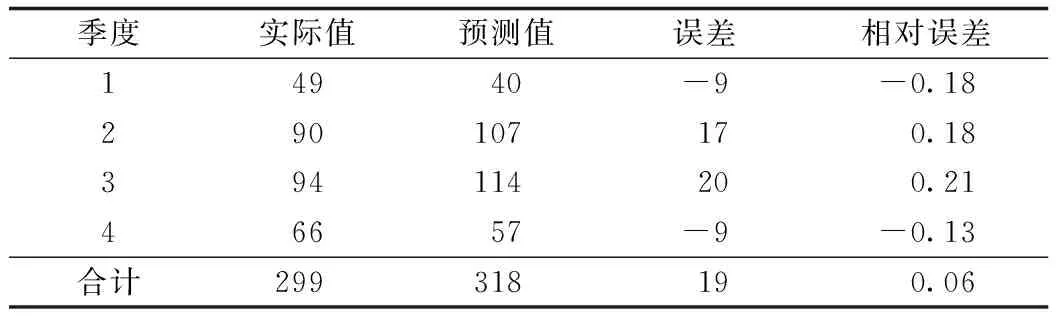
表1 2016年北京市食物中毒发生人数实际值与

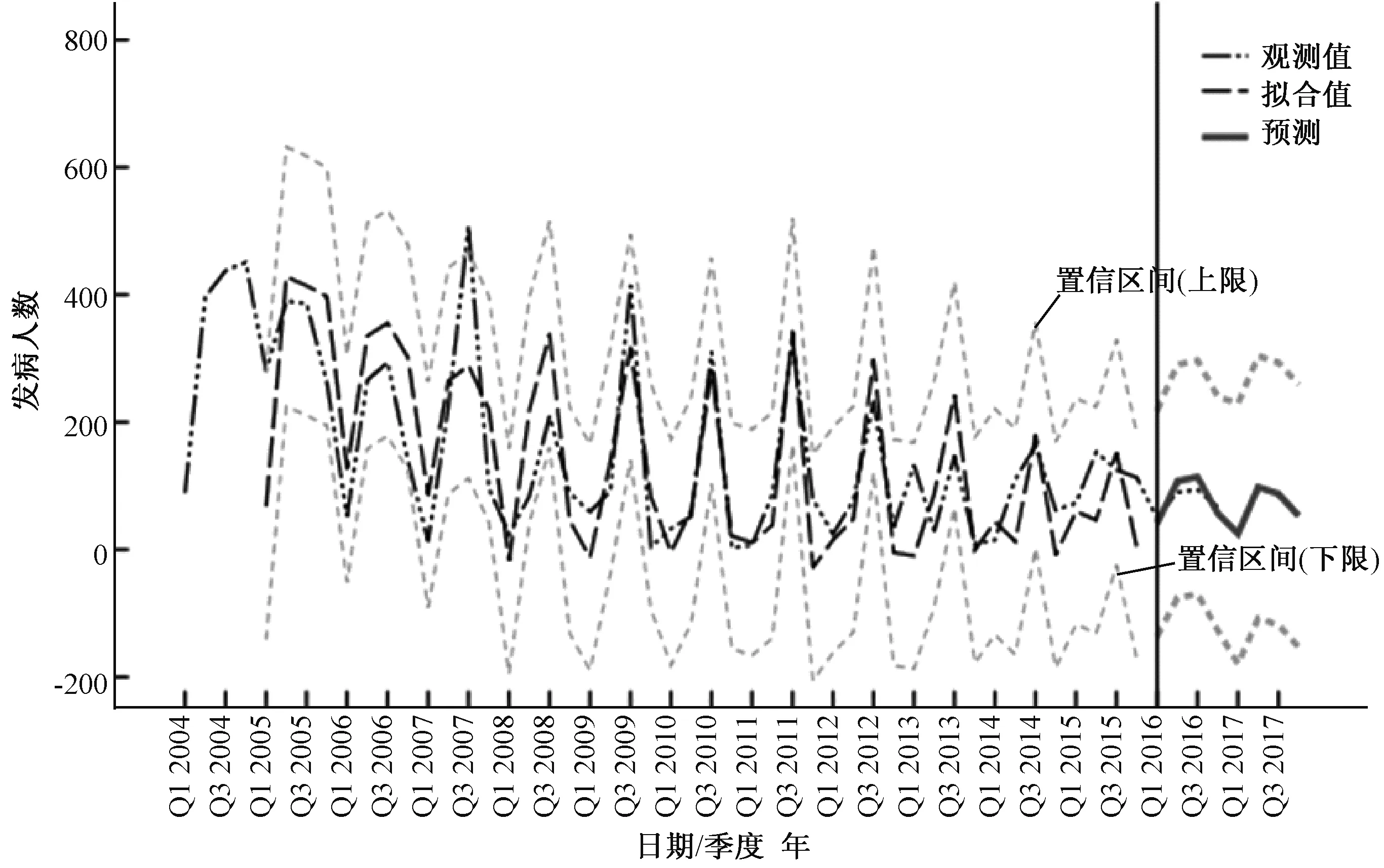
注：Q1为第1季度，Q3为第3季度。图6 北京市食源性疾病发生人数模型拟合序列图

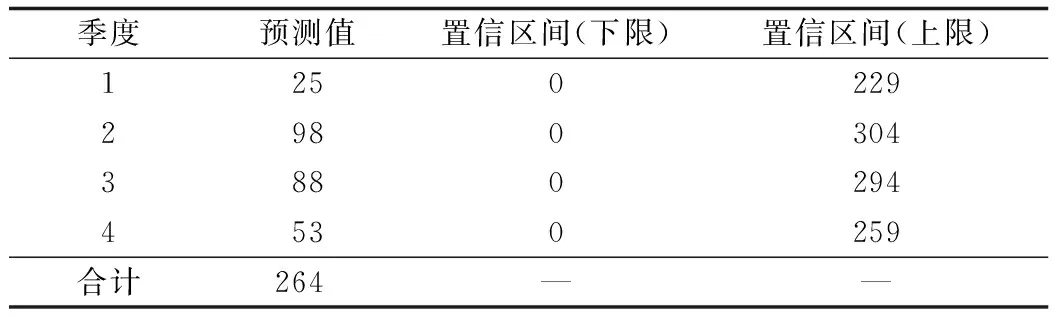
季度预测值置信区间(下限)置信区间(上限)1250229298030438802944530259合计264——

3 讨论

3.1目前用于疾病预测的模型很多，如多元回归分析、指数平滑分析等。与其他疾病相比，食物中毒影响因素较多，很难采用多元回归等模型对其进行预测。而时间序列模型能够充分利用一系列按时间顺序记录的数据，发现事物随时间变化的规律。ARIMA模型过程简便、短期预测精度较高，是目前应用较多的时间序列预测方法之一[2-6]。

3.2本研究选择了2004-2015年季度发病人数共48个数据建模，经过模型筛选，最终确立了ARIMA(1，0，0)×(1，1，0)4模型，并对2017年的发病情况进行了预测。结果表明模型可较好的拟合北京市食物中毒季度发病人数的变化规律，特别是在2010年以后预测的拟合值与实际值的走向基本一致，显示出较好的预测精度，各季度发病人数实际值都落入预测值的95%置信区间，说明运用ARIMA模型预测北京市食物中毒发病人数的变化趋势是可行的。不同研究在运用ARIMA模型对本地区数据进行拟合时，模型的预测误差不同，张爱红等[5]的研究拟合平均相对误差为2.70%，陈玲等[6]的研究为9.59%。本研究的中ARIMA模型预测误差为6.00%，可能与以下因素有关：一是用于建立模型的数据还不够多，二是某些年的食物中毒的发生受一些突发事件的影响。

综上所述, 可以运用ARIMA模型方法对北京市食物中毒发病人数进行预测，但值得注意的是食物中毒的发病人数受外界环境多种因素影响，要对其发生趋势进行更为准确的预测，还需要在模型中纳入其它影响因素。此外，单次分析建立的预测模型，只能用于短期预测。在实际工作中，应收集足够的时间序列数据，用新的实际值对已建立模型进行修正和重新拟合预测值，为科学制定食物中毒预防控制措施提供依据。

参考文献

[1] 孙振球，徐勇勇．医学统计学[M]．北京：人民卫生出版社,2002:351-372.

[2] 胡跃华，廖家强，冯国双，等．ARIMA模型在全国丙型肝炎疫情预测中的应用[J]．中国预防医学杂志,2015，16(4)：262-266.

[3] 朱平，侯晓艳，马平，等．南通市流感样病例时间序列分析及发病趋势的预测研究[J]．现代预防医学, 2015，42(1)：160-162.

[4] 高强，苏琦，范刚．ARIMA模型在2004-2014年淮安市其他感染性腹泻流行病学特征及发病趋势预测中的应用[J].中国预防医学杂志, 2016,17(14)：1953-1956.

[5] 张爱红，周培，申铜倩，等.乘积季节ARIMA模型在食源性疾病预测中的应用[J]．中国卫生统计，2014,31(1)：68-69.

[6] 陈玲，徐慧兰．自回归求和移动平均模型在湖南省食物中毒预测中的应用[J]．中南大学学报(医学版)，2012，37(2)：142-146.