一种利用振动响应识别裂纹转子参数的方法

史宏昊,冯长水



一种利用振动响应识别裂纹转子参数的方法

史宏昊,冯长水*

杭州电子科技大学机械工程学院, 浙江 杭州 310018

针对一类含裂纹的转子动力学特性及其参数识别，本文选取裂纹转子刚度模型——中性轴模型，提出适用于对中性轴模型的裂纹转子运动微分方程的求解方法，并研究了裂纹转子系统参数对动力学的影响。然后，采用反向求解思路，用龙格-库塔法拆分迭代裂纹转子运动微分方程，通过平均值法确定基因算法中的适应度函数，从而实现裂纹转子参数识别问题向求解动力学响应差异值最小化的最值优化问题的转化，最终使用基因算法对最值优化问题求解，并通过算例对该方法进行了验证，实现了低于0.6%相对误差的裂纹转子参数识别。

裂纹转子; 龙格-库塔; 参数识别; 基因算法

转子裂纹是一种旋转机械中较常见且危险的故障，但转子在出现裂纹后仍可以继续工作一定时间直至断裂或者达到刚度强度极限，这一段时间被称作裂纹转子的剩余寿命[1]。为充分利用裂纹转子的剩余寿命，达到最大经济效益，对裂纹转子中裂纹扩展与动态特性的在线监测逐渐发展起来，裂纹转子参数识别应运而生。

裂纹转子的参数识别是指基于己知系统的激励和响应求解该系统特性[2]。本文利用裂纹转子的振动输出识别裂纹是一个典型的反问题[3]，以反问题的求解思路和策略能更有效地解决这一问题。

本文以横向裂纹单盘对称Jeffcott转子作为研究对象[4]，裂纹在轴中部，时变刚度参考王宗勇等提出的裂纹刚度模型，即中性轴模型[5]。提出并发展适用于对中性轴模型下的裂纹转子运动微分方程的数值求解方法，应用该方法研究了裂纹转子系统中参数对动力学特性的影响。再采用反问题求解思路，使用龙格-库塔法拆分迭代裂纹转子运动微分方程，通过平均值法确定基因算法中的适应度函数，从而实现了裂纹转子参数识别问题向求解动力学响应差异值最小化的最值优化问题的转化；最终使用基因算法对最值优化问题进行求解，并通过两个算例对该方法进行了验证，实现了低于0.6%相对误差的裂纹转子参数识别。

1 中性轴模型下的裂纹转子运动微分方程

转子裂纹主要分为开裂纹与开闭裂纹，开裂纹指转动过程中裂纹保持开合状态，近似于不平衡量作用，开闭裂纹模型是指在转子运行过程中，裂纹随着轴转而进行开闭的状态，更能反映实际转子的运行情况[6]。裂纹转子动力学模型如公式(1)所示：

图 1 裂纹转子坐标系

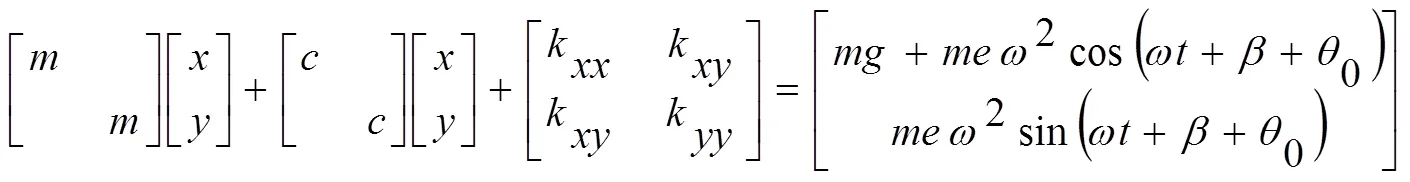
其中为质量偏心与裂纹方向之间的夹角，为质量偏心。

公式(2)即为无量纲化裂纹转子运动微分方程。

设裂纹转子系统中各参数[7]为：=25.4 mm，=32.1 kg，=2100 N∙s/m，=2.5×107 N/m，0=π。

其Matlab软件仿真结果如文献[7,8]。

2 基于遗传算法的裂纹转子参数识别

遗传算法(GA)是一种借助于自然遗传过程与生物的自然选择实现随机搜索的算法。该算法具有整体搜索特性、广泛性、含启发式的随机搜索以及无需借助辅助信息等特点[9]。其中适应度函数用于计算个体在群体中被使用的概率[10]。

通过模型仿真运算的数据与其实验数据具有统一性。本文将裂纹转子的参数识别作为一个反问题，并针对该反问题提出基于遗传算法的优化求解策略。该策略将裂纹转子参数识别这一反问题形式转化为以裂纹转子的实际振动响应与参数识别仿真结果的最小差值为优化目标的优化问题，进而利用遗传算法求解这一优化问题实现裂纹转子的参数识别。本文最后给出仿真研究对所提的方法和策略进行验证。

2.1 基于Runge-Kutta法的适应度函数

龙格-库塔(Runge-Kutta)方法[11]是一种在工程上应用广泛的高精度单步算法，此算法精度高，采取措施对误差进行抑制，属于数值解法中的一步法，即当计算y+1时，只用到前一步的值，适用于简化后的转子模型仿真计算；与当精度为4时，得到四阶龙格-库塔公式：

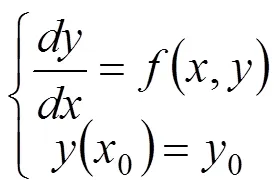
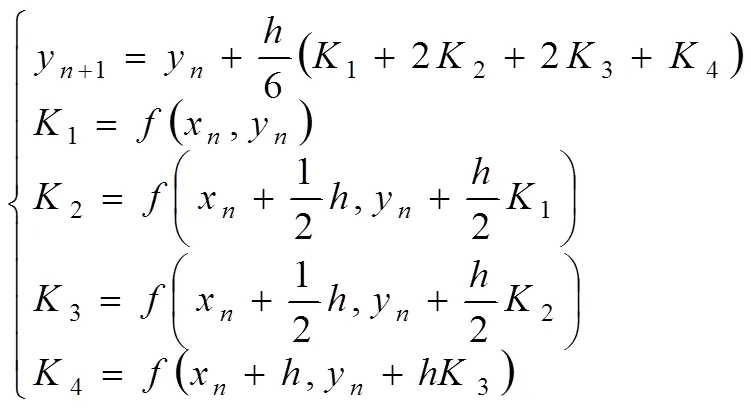
式中相邻两个点的间距=x+1-x称为步长，通过将高阶微分方程转化为一阶微分方程，然后通过迭代即可对该方程求解。

将裂纹转子运动微分方程组进行降阶，将裂纹角、质量偏心与裂纹方向夹角、无量纲化后质量偏心设为未知变量带入到龙格-库塔式中，即得到了含有上述三个未知变量的迭代公式。

已知响应，'，，'，分别对应轴位移、轴加速度、轴位移、轴加速度，用矩阵中a1，a2，a3，a4来表示，如式(8)所示

将矩阵中各项无量纲化后得到矩阵，其中b2=ɷa2、b4=ɷa4。

分别将矩阵中每一行项带入迭代，得到()矩阵，累加()并取均值，得到更为精确的迭代结果。

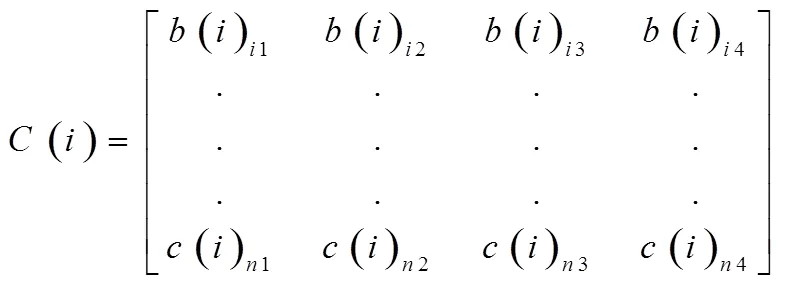
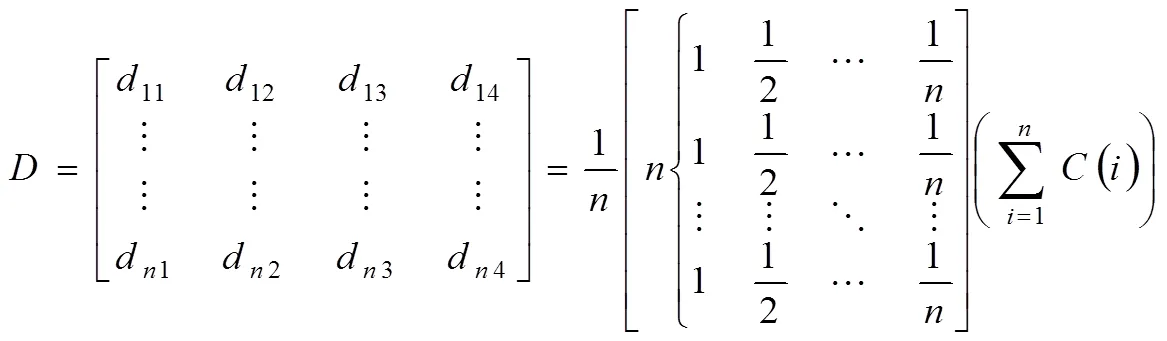
采用全局最优的方法，通过、矩阵中各项相对误差的累加来表示、矩阵中各个值的近似程度，即：

2.2 基于遗传算法解决最优化问题

选取无量纲化后，'，，'的作为染色体，因此其染色体数为4，适应度函数（Fitnessfun）如公式(9)所示

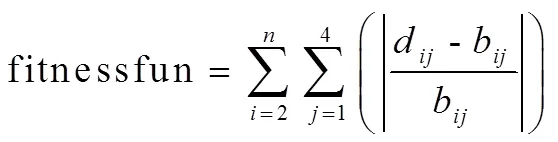
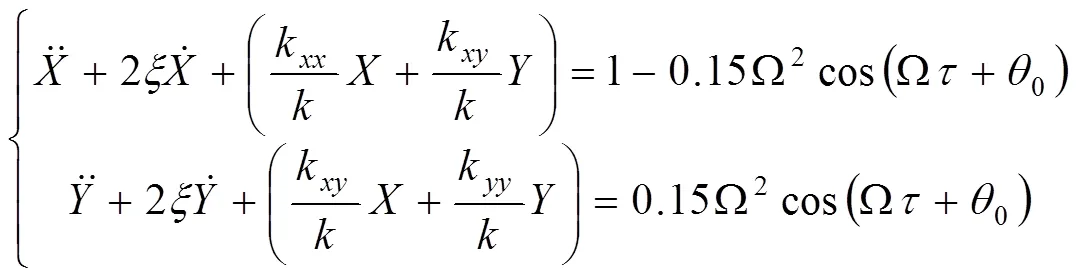
其稳定后的20组动力学响应结果由计算可得，用20×4的矩阵表示，

将矩阵中的数据带入矩阵中，其中=20，带入公式(10)，得到相对应的适应度函数，通过基因算法对裂纹转子系统中参数进行识别。识别结果如表1所示。

表 1 参数识别精度

识别后裂纹转子系统参数所对应的动力学响应用20×4的矩阵来表示。

矩阵与的裂纹转子系统动力学响应对比如图2所示，在所取的20组点处折线与星号基本重合，相比于算例一，算例二中动力学响应之间的差异值略微增大，通过多次试验后发现裂纹角的增大会导致动力学响应之间的差异值略微增大，但仍达到了参数识别的结果。

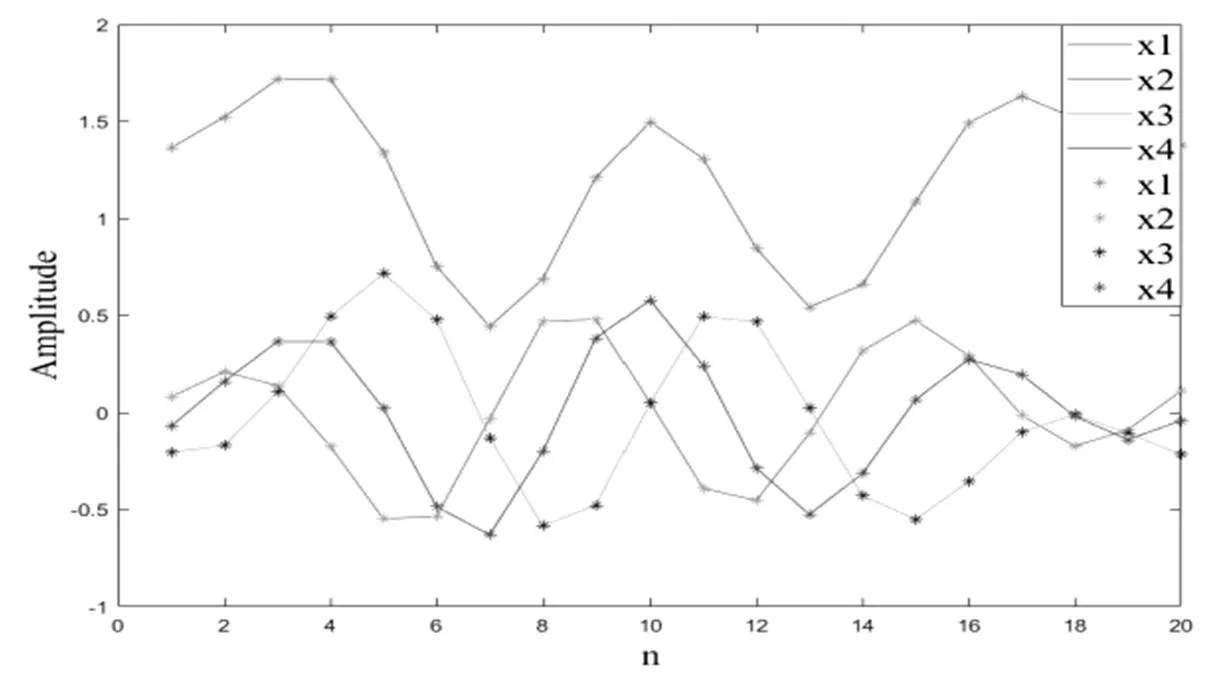
图 2 裂纹转子系统动力学响应对比图

3 结论

本文以含裂纹的转子系统为研究对象，建立刚性支撑裂纹转子模型，采用反问题求解思路，提出了一种基于遗传算法的裂纹转子参数识别方法，并通过遗传算法中的适应度函数改进，数值仿真得到更为精确的数值解，实现了最大相对误差低于0.6%。与传统的参数识别方法相比，该方法仅通过仪器测量出的响应（即坐标轴方向的位移及其加速度）就可以进行仿真计算，并且采用遗传算法求解，其易于实现、运算时间短以及精确性等特性使该方法具有一定的实用性和应用前景，可作为裂纹转子在线监测和诊断中的诊断手段。

本文只针对于Jeffcott转子模型情况，对于实际工况下的裂纹转子进行参数识别，还应在Jeffcott转子模型中考虑支承类型，对于油膜支承应加入非线性油膜力模型进行分析；还应考虑是否为多裂纹情况等等，上述模型已经实现实际运用，也适应于本文中裂纹参数识别方法。今后的研究应考虑一下几个问题：

（1）改进裂纹转子模型，使其更接近于所需工况，同时也适用于大尺寸裂纹情况；

（2）改进裂纹扩展模型，本文只是提出了理论上的裂纹扩展公式，实际工况下，应针对不同情况进行修正与扩充；

（3）将遗传算法与其他优化算法（比如模拟退火、蚁群算法等）相结合，提高其收敛性与精度。

[1] Wang CH, Brown MW. Life prediction techniques for variable amplitude multiaxial fatigue—Part 1: Theories[J]. Journal of Engineering Materials & Technology, 1996,118(3):367-370

[2] Belkheiri M, Rabhi A, Boudjema F,. Model Parameter Identification and Nonlinear Control of a Twin Rotor MIMO System - TRMS[J]. IFAC Proceedings Volumes, 2009,42(10):1487-1492

[3] Menshikov Y. Identification of Rotor Unbalance as Inverse Problem of Measurement[J]. Advances in Pure Mathematics, 2013,3(9A):20-25

[4] Kumar C, Rastogi V. A brief review on dynamics of a cracked rotor[J]. International Journal of Rotating Machinery, 2009,2009(2):1-6

[5] 王宗勇,林伟,闻邦椿.开闭裂纹转轴刚度的解析研究[J].振动与冲击,2010,29(9):69-72

[6] 高建,朱晓梅.转轴上裂纹开闭模型的研究[J].应用力学学报,1992(1):108-112

[7] 郭超众.具有呼吸裂纹的转子动力学特征提取及预诊方法研究[D].哈尔滨:哈尔滨工业大学,2014:23-41

[8] 朱厚军,赵玫,王德洋.Jeffcott裂纹转子动力特性的研究[J].振动与冲击,2001,20(1):1-4

[9] 杨丹,甘春标,杨世锡,等.含横向裂纹Jeffcott转子刚度及动力学特性研究[J].振动与冲击,2012,31(15):121-126

[10] Ishikawa T, Nakayama K. Topology Optimization of Rotor Structure in Brushless DC Motor With Concentrated Windings Using Genetic Algorithm Combined With Cluster of Material[J]. IEEE Transactions on Magnetics, 2012,48(2):899-902

[11] Hamdan M. Optimization of Small Wind Turbines using Genetic Algorithms[J]. International Journal of Applied Metaheuristic Computing, 2016,7(4):50-65

A Method Recognizing Parameters of a Cracked Rotor with Vibration Response

SHI Hong-hao, FENG Chang-shui*

310018,

Aiming at dynamic characteristics and parameter identification of a kind of cracked rotor, the stiffness model of the cracked rotor-neutral axis model was choosed to propose a numerical solution method for differential equations of cracked rotor under neutral axis model and study on the influence of parameters on dynamic characteristics of cracked rotor system. Then follow the inverse problem solution, the motion differential equation of cracked rotor was dismantled and iterated by using the Runge-Kutta method. The fitness function in genetic algorithm was obtained by using the average value method. Thus the transformation from the parameter identification problem of crack rotor to the optimal problem solving the minimization of the dynamic response difference value so as to realize the cracked rotor parameter identification problem solving the dynamic response to the most value optimization problem of minimizing the value difference. Finally, the genetic algorithm was used to solve the optimal problem and the example was used to verify the method. The relative error from parameter identification of the cracked rotor was realized below 0.6%.

Cracked rotor; Runge-Kutta; parameter identification; genetic algorithm

TB123

A

1000-2324(2018)03-0523-05

2017-02-10

2017-03-29

国家自然科学基金(11202061)

史宏昊(1992-),男,硕士研究生,主要研究方向为转子裂纹在线检测与分析. E-mail:794228483@qq.com

Author for correspondence. E-mail:csfeng@gmail.com