基于忆阻器交叉阵列的卷积神经网络电路设计

胡 飞 尤志强 刘 鹏 邝继顺

(嵌入式与网络计算省重点实验室(湖南大学) 长沙 410082) (湖南大学信息科学与工程学院 长沙 410082) (hu_qingfeng@126.com)

近年来，深度神经网络(deep neural network， DNN)在很多领域展现了独特的优势，比如计算机视觉、智能医疗、大数据处理、模式识别等.在2016年的“人机大战”中，由谷歌公司开发的基于深度学习工作原理的“阿尔法围棋”(AlphaGo)[1]以4∶1战胜韩国围棋高手，轰动一时.许多学者和百度、微软等高端互联网公司的研究表明深度学习在图像感知等方面的处理水平已经达到甚至超过了人类.

卷积神经网络(convolutional neural network， CNN)是目前研究最多、应用最为成功的一种多阶段全局可训练DNN模型，可以从经过简单预处理的数据甚至原始数据中学习到高阶的、抽象的、更接近本质的特征.CNN的提出在人工神经网络方向具有重要的里程碑意义，并且已经在人脸识别、车牌检测、目标跟踪和手写体识别等方面得到了广泛的应用.

DNN虽然可以取得很高的识别准确率，但网络复杂，需要大量的运算，消耗大量的能量与硬件资源.例如AlphaGo下围棋时，同时使用了上千个通用处理器和数百个图形处理器，每局棋耗电约3 000美元，这对大部分智能设备来说无法承受[2].目前，深度学习算法多在冯·诺依曼结构计算机上实现.冯·诺依曼机的基本特征为计算单元与存储单元分离，存储单元的低访问速度成为了如今计算性能提高的瓶颈.许多研究工作致力于给流行的机器学习算法设计加速器[3-4].

近几年，一种新型的器件——忆阻器引起了国内外学者的高度关注，被称为第4类基本电子元件，用来描述电荷与磁通量之间的关系[5-6].忆阻器可以根据流经自身的电荷量来改变阻值，具有存储[7]、逻辑运算[8-10]和模拟运算[11]等功能.

忆阻器可以实现学习与记忆功能，这种特性与神经网络中的突触有极大的相似性.忆阻器交叉阵列结构用于模拟量点积运算的想法引起了有关学者广泛的关注.研究表明采用模拟信号形式的交叉阵列结构比使用传统的高性能计算系统的计算性能更优[12].这使得忆阻器在神经网络计算方面具有独特的优势，为制造更快更节能且具有生物智能的模拟计算机带来了希望.

数字与模拟信号混合的忆阻器电路已经被广泛用于加速神经网络[13].2015年，一个可以实现准确点积运算的忆阻器交叉阵列结构与相应的编码方案被提出[14].2016年同一团队以实现1个卷积神经网络为目的，给出了更为详尽的设计方案[15].但是经过分析，该方案中的忆阻器交叉阵列并不能准确地存储偏置，然而偏置对神经网络识别效果作用很大.PRIME[16]是一个基于阻变式存储器(resistive random access memory, RRAM)的存内计算(processing-in-memory， PIM)结构，通过设计精细的外围电路来实现存储器的复用使得它可以高速地运行深度神经网络，其权值采用2个忆阻器单元分别存储正负权值[11].ISAAC(in-situ analog arithmetic in crossbar)[17]与PRIME都是以运行深度神经网络为目的，但是它们的数据编码与流水线设计完全不同.ISAAC把1个多位存储的数字拆分开来，用多个周期来进行不同位的运算，然后进行移位相加，同时忆阻权重的编码采用补码形式，避免了用2个阵列存储正负权重的方式.这种设计与软件实现具有相同的精确度，但是该设计并没有充分利用到忆阻器模拟元件的特性.并且此设计数模信号转换和模数信号转换频繁，数模转换器(digital-to-analog converter， DAC)和模数转换器(analog-to-digital converter， ADC)的面积开销较大.为了解决上述问题，本文主要有2个方面的贡献：

1) 提出1个改进的忆阻器交叉阵列结构，可以准确地存储权重与偏置.在末端连接1个反向放大器，结合相应的存储与编码方案，可以准确地实现神经网络中权重与偏置应有的作用.

2) 结合改进的忆阻器交叉阵列和CNN本身拥有的高容错性，设计了1个完整的CNN电路.其中，池化层的操作采用采样保持模块(sample and hold， SH)来暂存上层卷积操作的输出，然后直接进行池化操作，减少了1次数模-模数转换过程，减少了面积和识别时间.

本文基于忆阻器来研究并设计CNN电路，改变了传统的存储单元与运算单元分离的设计，实现了一部分数据存储与计算存在于1个单元，存在较大的理论与应用意义.本文的设计非常适合应用于DNN加速器，对将来人工智能技术产品化具有现实指导意义.

1 预备知识

本节首先对CNN模型进行简要的描述，然后简单介绍忆阻器应用于神经网络电路中的优势和忆阻神经网络.

1.1 卷积神经网络模型

CNN属于人工神经网络的一种，其隐藏层特殊的组织方式使得其在图像识别领域表现出优异的性能.受到生物视觉系统中局部敏感的启发[18]，CNN的设计引入了局部接受域，采用了接受矩阵数据作为输入的网络结构，并引入共享权重和池化(pooling)的想法来保证整个模型的性能[19].

如图1所示，一般CNN模型包括2个部分：特征提取部分和分类器部分.特征提取部分负责提取信息的特征;分类器部分负责对提取得到的特征进行识别,可以用贝叶斯网络等普通的神经网络模型来实现.下面主要介绍特征提取部分.

Fig. 1 Architecture of a CNN used for images recognition图1 用于图像识别的1个CNN结构

Fig. 2 Diagram of a convolution operation图2 卷积操作示意图

特征提取部分的基础结构包括2种隐藏层，即卷积层和池化层.卷积层可以被上层特征映射(feature map)的数量和尺寸、卷积核的尺寸和数量、跳跃因子、连接表等参数准确定义.如图1所示，第1个卷积层的输入是1张经过预处理后尺寸为28×28的图片，卷积核尺寸是5×5，向右和向下的跳跃因子都为1，提取出特征映射的尺寸是24×24.用6个卷积核分别对图片进行卷积，得到6张特征映射，相当于提取6种不同的特征.这里输入仅有1张图，输出有6张特征映射，所以连接表是1个1×6的全‘1’矩阵.

如图2所示，当执行卷积操作时，1个卷积核W在特征映射左上方根据跳跃因子参数的设定从左到右、从上到下进行移动.每次移动卷积核都对应特征映射上1个相同尺寸的局部接受域L′，L′与W相应位置上的数值进行乘法运算，再求和，加上偏置，最后通过激活函数得到1个新提取的特征值，存入下1层的特征映射中.

(1)

(2)

式(1)描述了图2这一时刻的计算过程.lp+i,q+j为局部接受域中的值，wi j为卷积核中相应的值，b′为偏置，y为提取的特征值，f( )为激活函数，一般取sigmoid函数，如式(2)所示.

池化层的目的是为了避免过拟合，一般取最大池化或平均池化.如图1第1个池化层操作过程为1张特征映射从左上方开始，从左向右、从上到下依次取相邻不重叠的2×2的局部接受域，最大池化即取这4个数的最大值，平均池化取这4个数的平均值，作为下1层的特征值.

1.2 忆阻神经网络

在生物和人工神经网络中，突触都是计算和信息存储的基本要素.1个人工神经突触需要记忆它的动态历史，通过前后神经元的神经活动来决定其存储的状态.图3描述了1个由忆阻器单元模拟生物神经元突触[20].忆阻器可以根据前后神经元的不同激活状态来自我调整忆阻器的阻值，这和生物神经突触的行为极为相似.

Fig. 3 Schematic illustration of using memristors as synapses图3 忆阻器突触的示意图

用忆阻器来实现突触主要有4个方面优势：

1) 忆阻器是无源器件，在断电后仍可以保持权值.

2) 忆阻器是模拟元件，其阻值存在最大值(称为Roff)和最小值(称为Ron)，且忆阻值可以在它们之间连续变化.这种特性更加符合生物突触状态的改变，并且具有更加强大的存储和计算功能.

3) 在传统的互补金属氧化物半导体(compl-ementary metal-oxide-semiconductor, CMOS)神经形态电路中，存储器与处理器之间的通信需要消耗时间与能量.忆阻器可以同时做存储与计算，缩短了响应时间.

4) 忆阻器可以与CMOS电路集成，CMOS构建神经元，忆阻器充当神经突触使得神经网络电路设计更加优越.

图4[21]是1个基于忆阻器交叉阵列的神经网络突触结构，模拟了4个前神经元与4个后神经元连接的中间突触，共包括16个突触，每个前神经元都和每个后神经元相连.输入信号以电压形式输入，突触权值以电导形式存储，根据欧姆定律可以实现输入电压Vin与忆阻器电导值G的乘法运算，又由于在电路中电流可以相加，则可以实现多个输入与多个权值的点积运算，再利用敏感电阻Rs读出电压，计算结果为

Vout=VinGRs.

(3)

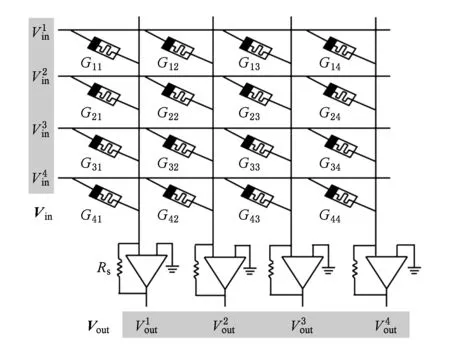
Fig. 4 Schematic of neuromorphic with memristor synapses in a crossbar configuration图4 交叉结构中的忆阻器突触的神经形态原理图

本文将使用忆阻器交叉阵列来存储卷积核和分类器的权重和偏置，并通过忆阻器的电路特性来实现原位的点积计算.

2 基于卷积运算的忆阻交叉阵列电路设计

使用忆阻器设计神经形态电路，主要用忆阻器替代神经突触，利用忆阻器的计算与存储特性，实现神经形态计算.本节提出了1个改进的忆阻器交叉阵列结构，通过增加3行忆阻器，可以更为准确地实现神经网络中普遍存在的点积运算.我们在电路中集成1个近似激活函数的器件可以实现神经元的功能.本节还改进了忆阻器的编码方案，进而设计了1个可用于卷积操作的忆阻器交叉阵列电路.

2.1 忆阻器交叉阵列中列电路设计

在神经元模型中，1个神经元同时接收多个前神经元发出的信号，进行相应的加权处理后，对神经元产生相应的刺激.图5展示了改进忆阻交叉阵列中1列(第j列)的详细设计，即网络中第j个后神经元与对其产生刺激的突触. 如图5所示，第j个后神经元与n个前神经元连接.神经元与神经元之间有刺激作用亦有抑制作用，映射到人工神经网络模型当中，突触权值有正值亦有负值.但是忆阻器的忆阻值只能为正，所以此设计同样使用前人2个忆阻值来存储1个权值的思路，这样设计可以实现与人工神经网络模型中相同的功能.将神经网络中权值矩阵W分为2个矩阵，分别将W中的正值的绝对值存储为W+，负值的绝对值存储为W-，W+与W-中其他的位置填充为0，既有：

W=W+-W-.

(4)

Fig. 5 Memristor crossbar column circuit图5 忆阻器交叉阵列中列电路突触电路示意图

如图5所示为神经网络中第j个后神经元对应的等效电路.因为反向放大器会使计算结果取反，本文中将负的权重矩阵W-存储进上半部分，上半部分对应的输入是原始信号，将W+存储进下半部分，下半部分的输入是取反后的原始信号，这样布局与之前学者的工作恰相反，可以得到1个正向的结果.

2.2 编码方案与神经元的设计

忆阻器的忆阻值并不能表示任意范围的实数，所以图5所示电路必须配合相应的编码方案才能发挥较好的作用.

理想状态下，忆阻器的忆阻值可以在最大值Roff和最小值Ron之间连续变化.本文根据2.1节提出的电路，对忆阻突触与偏置采用编码方案：

(5)

(6)

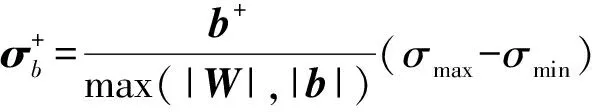
(7)

(8)

其中,σw和σb分别为存储权值和偏置的忆阻器编码后的电导值矩阵;σmax和σmin分别为忆阻器的最大电导值1Ron与最小电导值1Roff.分母为权值矩阵与偏置中绝对值最大的数的绝对值.⊕表示给矩阵中每一个元素加上一个常数.式(5)～(8)表示的编码方案可以表示任意权值和偏置.理想情况下这种编码方案可以实现准确的点积运算.

人工神经网络中，神经元的功能为接收前神经元输出的信号，进行处理，再发出信号.接收的信号为其所有前神经元的输出信号与相应权重的点积结果，处理为给点积结果加偏置，再将其输入激活函数，激活函数输出值即神经元的输出信号.

第2.1节中描述了点积与加偏置的过程.激活函数通常使用sigmoid函数，如式(2)所示.本文采用文献[15]中的方案，使用1个分段线性函数来代替sigmoid函数，分段函数为

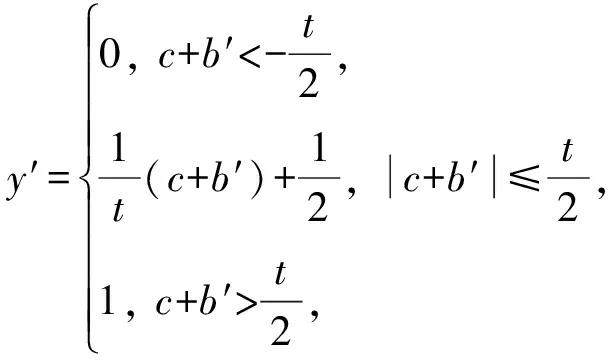
(9)

其中,c为点积结果，b′为偏置，二者之和为激活函数的输入值，1t为斜率，t的选取与实验中特征值的数据有关.当设t=10时，分段函数与sigmoid函数的比较如图6所示.图5中最后1行忆阻器与反向放大器部分可以实现此功能.

Fig. 6 Comparison of sigmoid function and linear function图6 sigmoid函数与分段线性函数的比较图

对反向放大器部分的忆阻器Ms进行编码：

(10)

经过计算可以得到:

(11)

(12)

经过上述设计，图5所示电路在理想状态下可以实现人工神经元模型的功能，即：

(13)

后续电路中设置最大电压为1V，最小电压为0V即可实现分段函数的功能.

2.3 忆阻交叉阵列电路设计

CNN中的突触是卷积核，由于CNN引入局部接受域结构，使得信号输入和神经元处理与上述情况略有不同.如图2所示，在CNN结构中，每个神经元的输入信号是1个方阵而不是1个向量.因此，我们需要把方阵拉直成向量形式来进行处理，如式(14)为起点位置p,q的3×3局部接受域的拉直处理：

(14)

CNN中卷积核结构设计如图7所示，其中局部接受域与卷积核的尺寸为n×n，卷积核同样需要拉直成1个向量，卷积核中的权值与卷积核对应的偏置值有正值也有负值，处理方法与图5相同.当1个局部接受域与卷积核是1个三维矩阵时，其操作与二维矩阵类似，最终都需要拉直成1个向量.然后把卷积核向量分成正值与负值2个向量，分别进行编码与写入.在电路运行过程中需要对输入信号进行取反，由于输入信号为模拟量，本文使用1个反向放大器来实现此功能，如图7所示，设置图中电阻R1与R2为相同值即可.在CNN中，每个卷积层包括多个卷积核，图7每列实现1个卷积核的功能，图7中共有k个卷积核.

Fig. 7 Diagram displaying the memristor crossbar design for convolution operation图7 处理卷积操作的忆阻器交叉阵列设计的示意图

经过这一部分详细的设计，图7所示的电路可以较为准确地实现1个局部接受域和卷积核尺寸为n×n，卷积核数量为k的卷积层的操作.基于此电路实现的卷积操作，具有高并行性.

3 忆阻卷积神经网络电路

本节将根据第2节中提出的忆阻器交叉阵列结构和编码方案，设计一个CNN电路结构，并且引入流水线技术来进一步提高所设计结构的性能.

3.1 总体结构

图8为设计的CNN电路整体结构.为了更加灵活地运行CNN算法，在1个加速芯片上设计了2种不同的计算单元C与C′，其中C是用来计算特征提取部分，C′是用来计算分类器部分.

如图8所示，每个计算单元C由1个静态随机存储器(static random access memory, SRAM)缓存、2个忆阻器交叉阵列结构(MC1与MC2)和2个池化存储(pooling and store, PS)模块组成.其中SRAM用于存储需要识别的信息(即CNN的输入);MC1与MC2分别用于存储CNN第1个卷积层与第2个卷积层的卷积核，并实现卷积操作.

Fig. 8 CNN architecture hierarchy图8 CNN整体电路结构层次图

当运行CNN时，从SRAM中将所需数据经过DAC传输给MC1，计算得到的模拟信号传送给PS. PS用来运行池化层的操作，并存储计算结果，这里是计算平均池化.如图8所示，PS结构由诸多小块组成，其数量与前面相连的忆阻器交叉阵列的列数相同(即卷积核的数量).每个小块由缓存、SH[22]、ADC和MC4这4个模块组成.由于CNN独特的网络结构，在网络正常运行时会生成大量的中间量，这些中间量存储在PS中的缓存中.

在卷积层与池化层之间，我们采用SH电路暂存卷积操作得到模拟信号，而不使用ADC变换后再存储.SH可以抓取MC1传送来的模拟信号并且保持，图8中MC4用于求尺寸为2×2的局部接受域特征值的平均值，所以每个SH模块有4个独立电路，分别抓取4个周期的输出结果，详细设计如图9所示.每个MC4都只由1列忆阻器组成，其中每1个输入线路都与1个独立的SH模块相连，每个交叉点采用1个忆阻器进行相连.取反部分和卷积核电路设计相同.

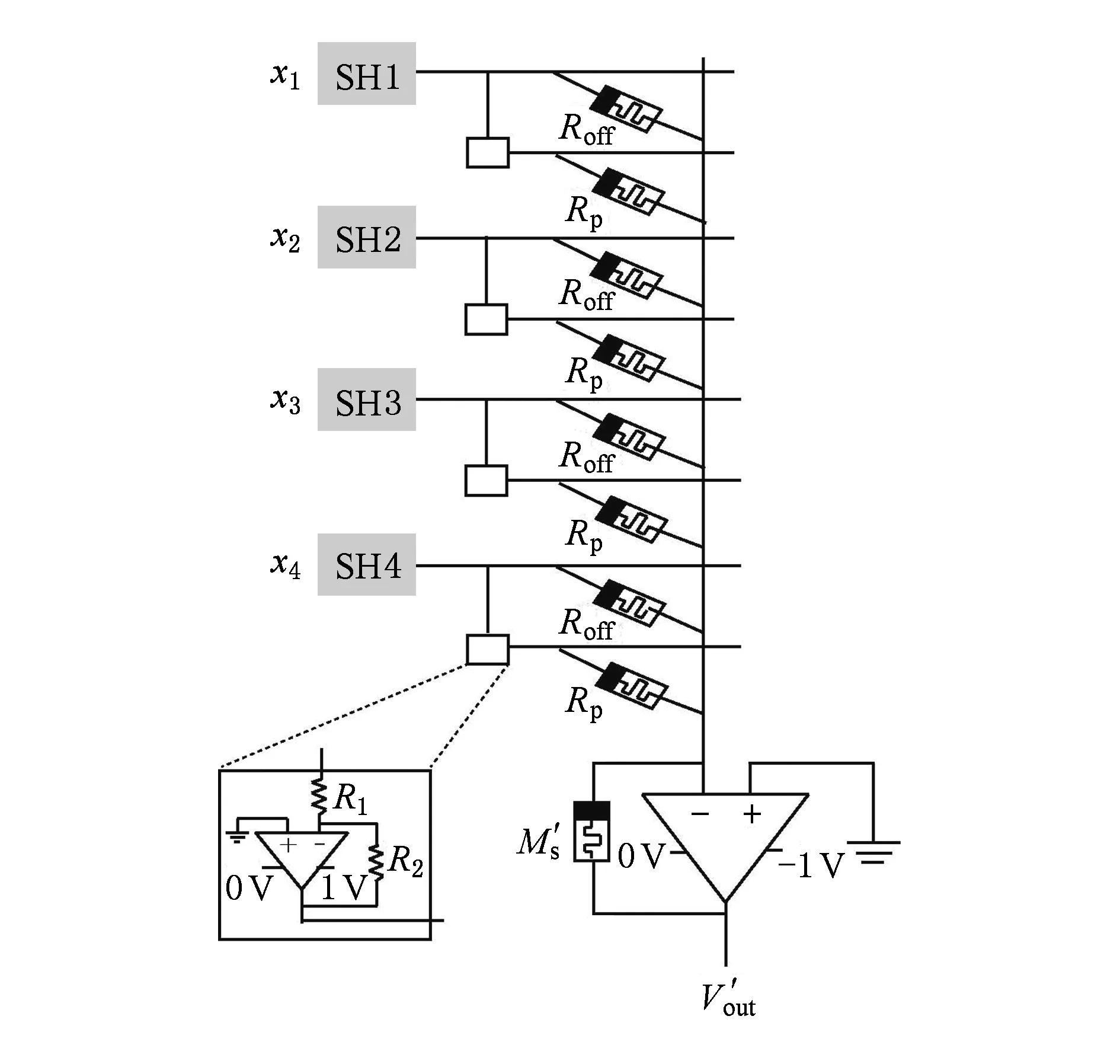
Fig. 9 Memristor crossbar used to compute ave-pooling图9 用于计算平均池化的忆阻器crossbar结构

卷积层每进行1次卷积操作会生成与卷积核数量相同的模拟信号，我们首先将其存入相应的SH模块中，等待满足要求再对其进行池化操作，这样和前人工作相比可以节省1组数模-模数转换过程.

求4个特征值的平均值可以看作2×2的局部接受域与大小为2×2元素都为1/4的矩阵做点积运算.因此，根据2.2节中的编码方案，对图9中各忆阻器编码：

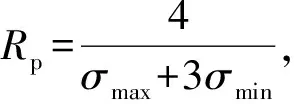
(15)

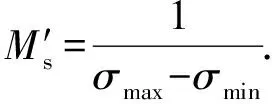
(16)

图9中，同样对信号进行取反，还有4个忆阻器都设为高阻态Roff，这样可以输出池化的结果，得到输出：

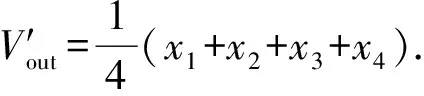
(17)

将输出信号进行模数转换存入缓存，等待进行第2层卷积操作.第2层卷积操作过程与第1次类似，只不过是在第1个PS模块所有的SRAM缓存中同时取相应的值输入MC2相应的DAC中.

C′模块用来完成分类器部分的计算，C部分提取的最终特征值都要传输给C′，由C′运行分类器部分的运算过程，得到最终结果.分类器部分采用普通的全连接网络.图8中C′部分由缓存、DAC,ADC和MC3组成.由路由装置将数据送入缓存，等待所需数据传输完毕，进行数模转换用MC3进行点积运算，再由模数转换成数字信号，经路由传送给外界，即运行完整个神经网络算法.

图8中1个路由同时连接3个C和1个C′，连接方式为硬连接，传输方向为从C到C′.由于在C′中只计算分类器部分，其运行周期数比C中特征提取部分的周期数少很多，所以在电路设计时可以给多个C匹配1个C′.

3.2 引入流水线技术

根据图1中描述的网络结构，以1张大小为28×28的图像为例，分析CNN的数据流动过程.在进行第1个卷积层的操作时，特征映射图中的特征值逐渐生成，如图10所示，左边特征映射中特征值1～26已经计算得到.此时虽然第1个卷积层的所有操作没有完成，但已经具备进行后面池化层的所有条件.在此时开始运行池化层的操作，既可以降低整个CNN算法运行的时间，又可以减少必要的缓存空间.

Fig. 10 Diagram displaying the pipe-line of feature values图10 特征值流水线示意图

上述流水线技术还可以改进，本文采用以池化部分的局部接受域为跳跃生成目标来进行卷积操作.如图10所示，即原始CNN卷积层的卷积过程都为从左至右、从上至下，本工作采用从左到右先生成1～2，然后再下跳生成25～26，这样可以符合SH的电路要求，也可以降低3～24部分的存储空间需求.

4 实验与结果分析

4.1 识别性能分析

实验采用如图1所示的CNN结构.参数设置如下：输入为28×28的灰度图片，第1层卷积层有6个5×5的卷积核，卷积操作中卷积核向右与向下移动，跳跃因子为1，2个池化层都是无交叉的2×2的局部接受域求平均的操作;第2个卷积层有12个5×5×6的卷积核;最后的分类器采用无隐藏层的简单全连接神经网络.

本实验采用MNIST数据集，包含70 000张手写体数字图片.实验中将其分为2部分，将其中60 000张作为训练集来训练CNN，其他10 000张作为测试集来测试训练结果以验证我们设计电路结构的有效性.

训练过程中以50张图片为单位，对训练集进行100次迭代训练，对权重及偏置进行更新，得到权重与偏置中的最大绝对值分别为4.927 9与4.719 3.如果我们将权重的最大绝对值设为大于4.927 9的任一个数，理论上可以使用本文设计的电路结构和编码方案来准确实现测试过程，但是对忆阻器进行写操作时本就存在误差.由图11可以看到权值与其对应编码的阻值对应是非线性关系，当最大绝对值是5时权值绝对值范围0～2.5由忆阻器超过99%的电阻范围来表示，根据图12权值分布有98%的权重在0～2.5之间，这样的分布可以使我们较为准确地对忆阻器进行写操作.我们也可以通过调整最大绝对值来更好地利用忆阻器电阻范围.

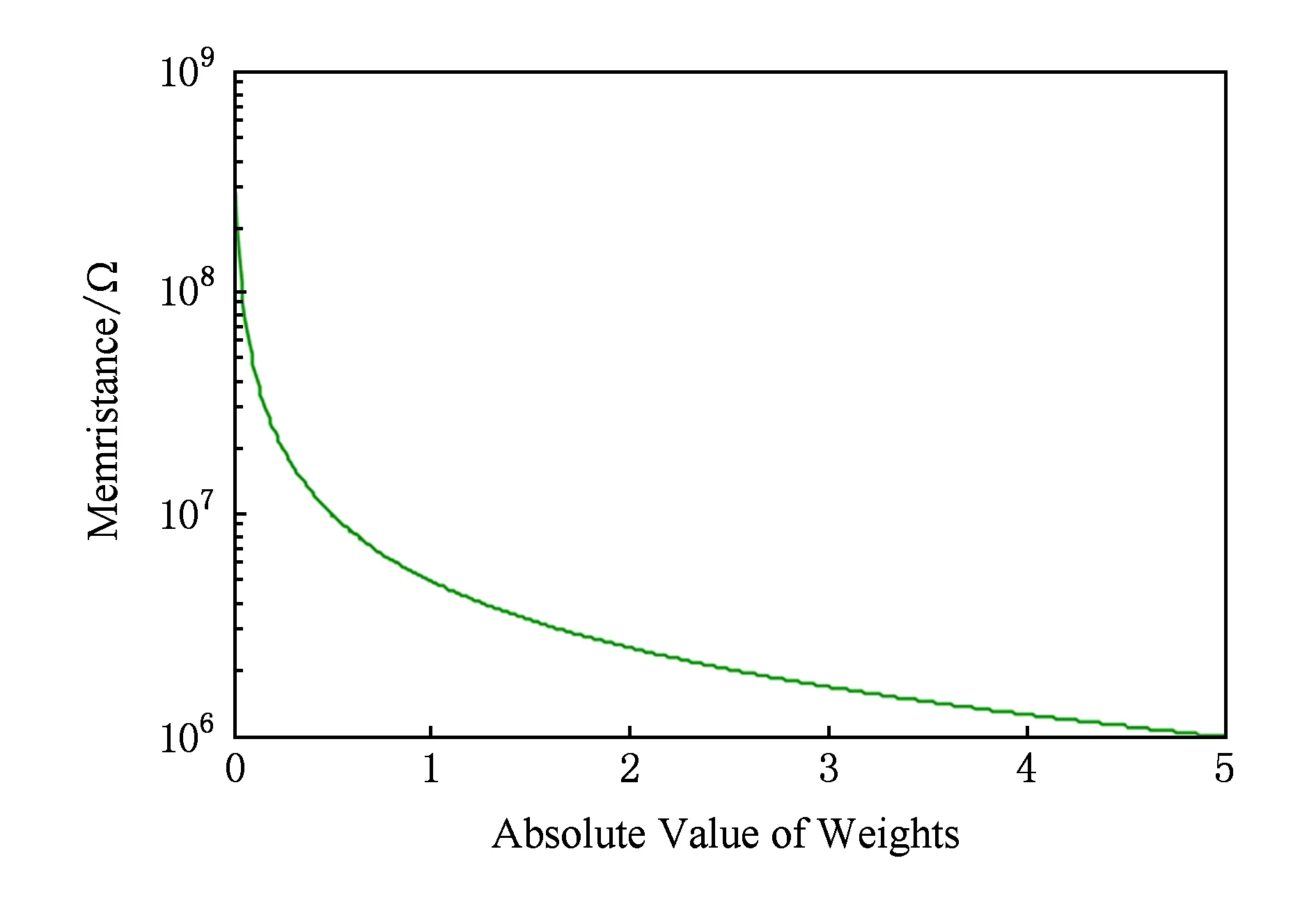
Fig. 11 Weights and memristance after encoding图11 权值与编码后对应的忆阻值

Fig. 12 Diagram displaying of weight distribution图12 权值分布图

实验中采用了1个简单线性的忆阻器模型[23]：

(18)

其中,δr代表忆阻器阻值的最大值Roff与最小值Ron的差值，δt代表时间最小步，Vm为施加在忆阻器上的电压值，Vth,pos是忆阻器的正向电压阈值，Vth,neg是忆阻器的负向电压阈值，tneg是忆阻器的阻值从Ron增加到Roff所需要的转换时间，tpos是阻值从Roff到Ron所需要的时间.参数设置如表1所示.写操作采用文献[15]中的写电路，考虑到忆阻器制作工艺不成熟，在本文的仿真实验中加入1 b写随机噪声，使得忆阻器的表示精度降低1 b.

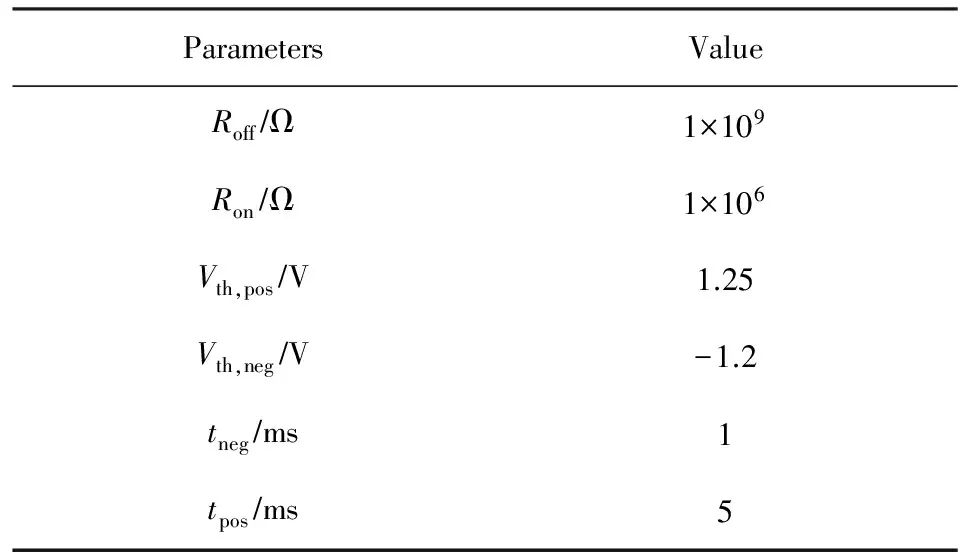
Table 1 Memristor Parameters表1 忆阻器参数

Fig. 13 Comparison chart of recognition error rate for different numbers of bit memristor图13 不同存储位数忆阻器的识别误差比较图

对实际的忆阻器物理器件，编码后进行写操作并不能准确地实现理想的状态调整，会存在读写噪声.实验中分别对忆阻器存储大小为4 b，6 b，8 b[16]信息的情况进行了仿真实验，并在实验中加入了随机噪声因素来比较各自的误差率，如图13所示.软件环境下测试集的误差率为1.08%，根据图13所示，随着迭代次数的增加，3个实验的误差率总趋势都越来越低.其中单个忆阻器能表示的信息越多，电路运行结果与软件结果越接近.由实验结果得出单个忆阻器存储6 b与8 b的电路实验结果中的误差率与软件实验结果中误差率的平均差距分别增加了0.039%与0.012%，可以得出与软件实验极其相似的结果.这也体现了CNN具有极好的容错性，在电路设计中忆阻器存储值存在微小的偏差不会对识别结果产生较大影响.

4.2 电路性能分析

在只考虑流水线的情况下，使用ISAAC[17]结构运行如图1所示的CNN.每次卷积操作需要22个周期完成，每个池化操作需要5个周期，完成图1所示的算法需要11 001个周期.文献[17]设置的周期为100 ns，即时钟频率为10 MHz.本文为了实验的可比较性，同样采用10 MHz的频率.采用本文设计的电路结构，使用1个C计算单元来计算特征提取部分，然后使用C′来识别，只需1 162个周期.

在考虑分布式的情况下，在GPU上实现ISAAC可以将1个卷积层的操作分布到不同的忆阻器交叉阵列结构中进行运算.ISAAC中1个tile可以同时运行48个图1所示同参数的CNN.1个tile的面积为0.372 mm2，1个芯片一共集成了168个tile，总面积为88 mm2.

为了比较上的公平，本文与ISAAC一样，使用CACTI 6.5在32 nm工艺下模拟各个buffer的面积，片外连接采用与ISAAC相同的方式.ISAAC没有给出忆阻器面积的估算方式，文献[24]给出在CMOS 65 nm工艺下，忆阻器面积可达10 nm×10 nm.考虑到金属线之间的间隔，本文对单个忆阻器的面积用20 nm×20 nm进行估算.注意到，相对于CMOS器件，忆阻器的面积很小，忆阻器交叉阵列的面积在整个电路中所占比例很小，对芯片面积的影响几乎可以忽略.各个部件参数及面积如表2所示，芯片总面积如表3所示.我们集成1 500个C与100个C′，总面积为62.37 mm2，加上片外面积共85.25 mm2.可并行运算1 500个整套图1中的CNN.

表4显示分别用软件，ISAAC和本文设计结构测试10 000条手写体数字的识别时间.其中使用软件运行时，我们在TensorFlow和CUDA的环境下采用python语言来编写程序.硬件配置为Intel CoreTMi7-6700K CPU@4.00 GHz×8，GPU 为 GeForce GTX 980，系统字长为64位.由表3和表4可以得出，本文设计的结构在相同面积的基础上运算速度是ISAAC的7.7倍.在1个不到1 cm2的芯片面积上，本文提出电路结构的运算速度比如上配置的单机快1 770倍.

Table 2 Structure Parameters表2 结构参数

Table 3 Chip Parameters表3 芯片参数

Table 4 Recognition Time Comparison表4 识别时间比较 s

5 结 论

本文采用数字-模拟混合信号的形式，利用忆阻器与传统CMOS器件结合设计出了1个可以实现完整CNN的电路结构.本文首先提出了1个改进的可以实现神经网络算法中普遍存在的点积运算的忆阻器交叉阵列电路.然后将此电路分别用于CNN中的卷积核、池化与分类器部分，设计出了1个可以完成具有2个卷积层和池化层的CNN电路.实验结果表明设计的结构大大降低了算法运行时间与硬件开销，仅存在微小的识别误差开销.

忆阻器作为1个新兴的器件，在纳米级工艺下与传统器件相结合设计电路时，受到了现有技术与传统器件的制约，其电路设计潜力尚未完全展示.下一步我们将开展用忆阻器来设计实现性能更高的CNN加速器，并实现原位训练.

[1]Silver D, Huang A, Maddison C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489

[2]Tao Jianhua, Chen Yunji. Current status and consideration on brain-like computing chip and brain-like intelligent robot[J]. Bulletin of Chinese Academy of Sciences, 2016, 31(7): 803-811 (in Chinese)

(陶建华, 陈云霁. 类脑计算芯片与类脑智能机器人发展现状与思考[J]. 中国科学院院刊, 2016, 31(7): 803-811)

[3]Wang Ying, Xu Jie, Han Yinhe, et al. Deepburning: Automatic generation of fpga-based learning accelerators for the neural network family[C] //Proc of the 53rd Design Automation Conf (DAC’16 ). Piscataway, NJ: ACM, 2016: Article No.110

[4]Wang Ying, Li Huawei, Li Xiaowei. Re-architecting the on-chip memory sub-system of machine-learning accelerator for embedded devices[C] //Proc of the 35th Int Conf on Computer-Aided Design. New York: ACM, 2016: Article No.13

[5]Chua L. Memristor-the missing circuit element[J]. IEEE Trans on Circuit Theory, 1971, 18(5): 507-519

[6]Strukov D B, Snider G S, Stewart D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80-83

[7]You Zhiqiang, Hu Fei, Huang Liming, et al. A long lifetime, low error rate RRAM design with self-repair module[J]. Journal of Semiconductors, 2016, 37(11): 94-98

[8]Wang Ying, Han Yinhe, Zhang Lei, et al. ProPRAM: Exploiting the transparent logic resources in non-volatile memory for near data computing[C] //Proc of the 52nd Annual Design Automation Conf. New York: ACM, 2015: Article No.47

[9]Borghetti J, Snider G S, Kuekes P J, et al. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication[J]. Nature, 2010, 464(7290): 873-876

[10]Liu Bosheng, You Zhiqiang, Li Xiangrao, et al. Comparator and half adder design using complementary resistive switches crossbar[J]. IEICE Electronics Express, 2013, 10(13): Article No.20130369

[11]Li Boxun, Yi Shan, Hu Miao, et al. Memristor-based approximated computation[C] //Proc of the 2013 Int Symp on Low Power Electronics and Design. Piscataway, NJ: IEEE, 2013: 242-247

[12]Taha T M, Hasan R, Yakopcic C, et al. Exploring the design space of specialized multicore neural processors[C] //Proc of the 2013 Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2013: 1-8

[13]Prezioso M, Merrikh-Bayat F, Hoskins B D, et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors[J]. Nature, 2015, 521(7550): 61-64

[14]Yakopcic C, Hasan R, Taha T M. Memristor based neuromorphic circuit for ex-situ training of multi-layer neural network algorithms[C] //Proc of the 2015 Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2015: 1-7

[15]Yakopcic C, Alom M Z, Taha T M. Memristor crossbar deep network implementation based on a convolutional neural network[C] //Proc of the 2016 Int Joint Conf on Neural Networks. Piscataway, NJ: IEEE, 2016: 963-970

[16]Chi Ping, Li Shuangchen, Xu Cong, et al. PRIME: A novel processing-in-memory architecture for neural network computation in reram-based main memory[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 27-39

[17]Shafiee A, Nag A, Muralimanohar N, et al. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 14-26

[18]Hubel D H, Wiesel T N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex[J]. The Journal of physiology, 1962, 160(1): 106-154

[19]LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324

[20]Jo S H, Chang Ting, Ebong I, et al. Nanoscale memristor device as synapse in neuromorphic systems[J]. Nano Letters, 2010, 10(4): 1297-1301

[21]Hu Miao, Strachan J P, Li Zhiyong, et al. Dot-product engine for neuromorphic computing: Programming 1T1M crossbar to accelerate matrix-vector multiplication[C] //Proc of the 53rd Design Automation Conf (DAC’16 ). Piscataway, NJ: ACM, 2016: Article No.19

[22]O’Halloran M, Sarpeshkar R. A 10-nW 12-bit accurate analog storage cell with 10-aA leakage[J]. IEEE Journal of Solid-State Circuits, 2004, 39(11): 1985-1996

[23]Wang Weiwei, You Zhiqiang, Liu Peng, et al. An adaptive neural network A/D converter based on CMOS/memristor hybrid design[J]. IEICE Electronics Express, 2014, 11(24): Article No.20141012

[24]Govoreanu B, Kar G S, Chen Y Y, et al. 10×10nm2Hf/HfOxcrossbar resistive RAM with excellent performance, reliability and low-energy operation[C] //Proc of the 2011 IEEE Int Electron Devices Meeting. Piscataway, NJ: IEEE, 2011: 729-732