基于混合编码的FPGA系统配置文件压缩算法
伍卫国 王超辉 王今雨 聂世强 胡 壮
1(西安交通大学电子与信息工程学院 西安 710049) 2 (国家数据广播工程技术研究中心(西安交通大学) 西安 710049) (wgwu@mail.xjtu.edu.cn)
近10年来,普适计算和物联网的兴起促进了嵌入式系统的发展,基于嵌入式系统的应用正在迅速占据着传统IT行业的市场份额.可重构计算(reconfigurable computing, RC)是继通用计算和专用集成电路(application specific integrated circuit, ASIC)之后的第3种计算模式,其综合了通用计算与ASIC的优点,一定程度上实现了计算速度与灵活性的并存.使用可重构计算技术的系统被称为可重构系统,主流的可重构系统依托于现场可编程门阵列(field programmable gate array, FPGA),实现了硬件资源的重复使用.在嵌入式应用中,可重构系统已经应用到汽车、医疗、广播、航空航天、高性能计算、数据存储、无线通信以及家庭网络等领域中,其应用价值的重要性不言而喻.
经典动态可重构系统模型如图1所示,其中包括应用任务的软硬件划分、调度与布局、布线、加载以及运行五大部分(如图1中虚线框1~5).应用程序中的任务按照自身属性,由任务划分器划分为软件任务或者硬件任务,软件任务添加到软件任务队列中,然后在软件运行环境中(一般为CPU)运行;硬件任务的执行需要经过5个阶段:1)硬件任务的调度.虚线框1为任务的调度过程.2)调度后的任务根据硬件资源需求,由布局器布局在FPGA的某块空闲资源区中,虚线框2中即为任务的调度与布局部分.3)布局后的任务需要与I/O资源或者内部其他硬件资源通信,这就涉及到重新布线的问题,虚线框3中为任务的布线部分.4)当布线完成后,需要将新生成的二进制配置文件配置到FPGA可重构资源的存储区中,确定各个可重构资源的逻辑功能,虚线框4为二进制配置文件的加载过程.5)当任务被配置到FPGA上,按照预先定义的逻辑功能运行,直到任务计算完成,虚线框5为任务在FPGA上运行过程.
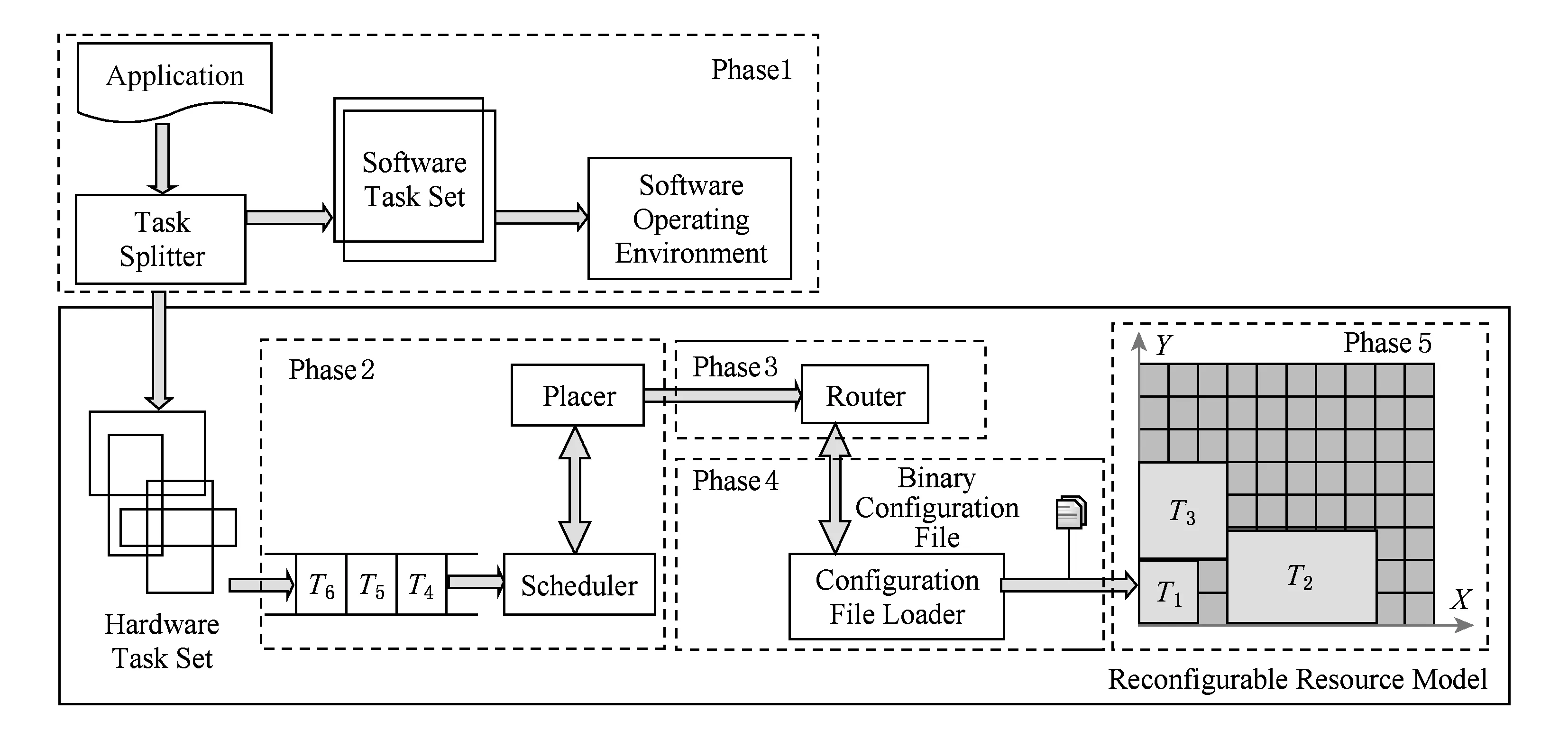
Fig. 1 Flow chart of classical dynamic reconfigurable system图1 经典动态可重构系统流程图
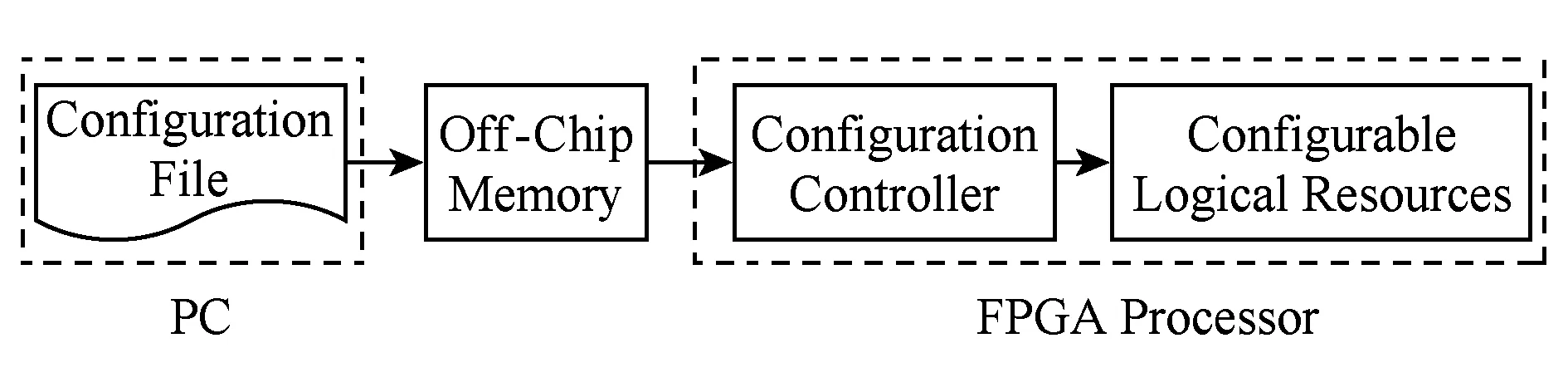
Fig. 2 Reconfigurable file configuration process (no compression)图2 可重构文件配置过程(不含压缩)
随着大规模集成电路技术的迅猛发展,FPGA工艺也在不断提高.Xilinx公司于2003年推出的Spartan3系列处理器采用90 nm工艺,到最新的VIRTEX系列可编程FPGA系列采用16~28 nm工艺.工艺上的提升不仅降低了能耗,最主要是增加了集成度,Spartan3系列处理器中的逻辑单元(logic cells, LC)个数最多为53 712个,而Virtex UltraScale处理器中LC数量为4 432 680个,与之对应的配置文件大小相当Spartan3系列处理器配置文件大小的82倍.考虑到其他硬件资源(I/O资源、布线资源、DSP资源、存储器资源和硬核微处理器资源等)的增加,近10年配置文件大小已经增加了百倍以上[1].图2为不含压缩过程的配置文件配置过程,在该过程中,主要有2个阶段耗时:1)配置文件从片外存储器或PC机传送到片内配置控制器(配置存储器);2)配置过程,即在配置控制器作用下将配置信息写入可编程逻辑块中并进行初始化操作(可编程逻辑块、寄存器、I/O缓存).JTAG(joint test action group)为FPGA常见配置文件下载方式之一.JTAG下载方式为串行传输模式,在测试时钟一定的情况下,配置文件传输时间完全由配置文件大小决定.这样,为了减少第1阶段耗费的时间,目前的解决方案为压缩配置文件.各大可编程逻辑设备(programmable logic device, PLD)制造商(Xilinx,Intel等)也意识到了压缩配置文件的重要性,在配置文件生成阶段都可以设置配置文件压缩方案.图3为含压缩过程的配置文件配置过程:
现在主流的FPGA处理器考虑到设计的安全性,对配置文件也进行了加密处理,这样可以防止设计拷贝以及逆向工程等非法操作.Xilinx公司和Intel公司FPGA处理器均采用了256b AES对称加密算法[2-3].加密解密消耗的时间不仅与算法本身相关,而且与加密文件大小相关.在加密前对配置文件进行压缩处理,可以大幅度减少加密和解密过程的时间代价.Xilinx公司和Intel公司最新FPGA处理器同时支持配置文件压缩与加密.由此可见,采用压缩方法对于解决第1阶段的耗时性还是很有帮助的.
1 国内外现状研究
可重构系统配置文件压缩技术的使用不仅在一定程度上减少系统配置时间,提高系统运行速率,满足实时性应用需求,而且降低了配置控制器内部存储代价,节约存储资源.对于配置文件压缩必须满足2个条件:1)无损压缩;2)解压算法实现代价低.在FPGA二进制配置文件配置过程中,最小的配置单位为帧.配置帧中的每1b二进制数据都代表着芯片中某个可配置资源中寄存器的高低位,即配置帧信息的改变就有可能改变可配置资源的功能.为了保证可重构系统正常运行和可重构模块功能不受改变,压缩算法必须采用无损压缩方式.配置文件经过压缩后可以在一定程度上减少系统配置时间,但并不是配置文件经过压缩处理过后就能够提高配置速率,解压缩过程也是很重要的一个环节.若解压缩过程所消耗的时间代价过大或者消耗硬件资源过多,那么该压缩算法就不适合对配置文件压缩.近几年,国内外学术界对压缩配置文件提高可重构系统配置速率展开了广泛的研究,现有的压缩技术分别侧重4个方面:压缩算法、降低解压缩代价、动态可重构和修改硬件结构.
1) 提升压缩率
研究主要集中在通过改进经典的压缩算法降低配置文件压缩率,从而达到提高配置速率、减少存储代价为目标.Vliegen等人[4]提出一种基于单片机远程配置FPGA的解决方案,其压缩算法采用了行程编码压缩算法,该算法易于实现并且可以达到较为理想的压缩效果;Tefan[5]针对Xilinx公司Virtex 4系列FPGA器件提出了2种专用压缩算法,基于LZW的压缩算法和基于二进制算术编码器压的缩算法,该作者使用了较少的硬件资源分别实现了这2种压缩算法;有些学者通过提出新的配置环境或者划分配置文件等预处理操作,然后结合基于字典的压缩算法实现高压缩比[6-7];Jia等人[8]通过在JTAG配置模式中分别增加基于定长行程编码与解码方案实现配置文件的压缩与解压缩;采用该种思路的还有文献[9-11].从压缩算法出发来解决配置文件压缩的优势在于可以充分利用压缩文件自身的特征,结合现有的优秀压缩算法进行压缩处理,获得较为理想的压缩率.但是,这往往会导致在提高压缩率的同时忽略了解压缩过程在配置过程中的重要地位,造成解压缩电路复杂,时间开销大.
2) 降低解压缩代价
FPGA中的配置控制器需要对可配置资源中所有可编程资源进行重新配置,需要输出完整的配置信息,因此解压缩过程是必要的环节.解压缩算法是通过FPGA内部硬件逻辑资源实现的,解压缩算法的性能与复杂程度也是严重影响配置性能的关键因素之一.国内外许多学者以解压缩效率为重点研究目标,对压缩算法进行了大量研究.Jafri[12]采用LZSS压缩算法对配置文件进行压缩,其优势在于可以针对LZSS算法实现高效的并行解压缩算法;Qin等人[13]提出了一种具有解压感知的压缩算法,目的是为了更高效的完成解压缩算法;Nabina等人[14]在传统的配置控制器里结合了基于ICAP (internal configuration access port)优化的解压缩算法,实现了高速率的配置文件解压缩过程;Jordan等人[15]从硬件实现角度进行改进,通过将固定硬件实现解压算法与基于LUT实现解压算法相结合的思想达到了灵活性与资源代价平衡的目的.
3) 动态可重构配置
动态可重构系统配置文件由2部分构成:静态可重构区域配置信息和动态可重构配置信息.静态可重构区域配置信息完全相同,对多个配置文件而言这部分内容为冗余数据.许多研究者就从这个角度出发进行关于动态可重构系统配置文件压缩研究.Liu等人[16]实现了基于FPGA重构技术的雷达信号处理系统,通过分析雷达信号处理的核心算法,找出不同算法对应配置文件的重复部分并删除,达到压缩配置文件的目的;Sellers等人[17]对静态可重构部分的配置信息进行了分析,通过删除初始化配置信息中所有“0”帧信息和相关的写入命令达到了压缩初始化配置信息的目的;Gu等人[18]从3个层次进行配置文件压缩:配置帧内、配置帧间和配置文件级压缩;Beckhoff等人[19]通过分析静态可重构区域配置信息和动态可重构配置区域各自的特征,对这2部分采用不同的压缩算法以提高整体压缩率.
4) 修改硬件结构
还有一些压缩方案是通过修改配置系统结构或者考虑其他配置因素从而进一步提高压缩率.Xie等人[20]用可寻址配置文件寄存器替代传统移位寄存器,并且在FPGA内部实现了以帧为单位的解压电路,从而提高了配置速率.
本文依据各种压缩思路的优缺点,选用行程编码压缩思想(run length encoding, RLE)为核心对配置文件进行压缩.首先通过统计配置文件信息,确定定长RLE压缩算法相关参数.然后对定长RLE压缩算法进行优化,结合Huffman编码方式实现变长RLE压缩算法.最后,采用掩码思想对变长RLE压缩结果进行2次压缩,进一步降低压缩率.
2 配置文件压缩算法
FPGA配置文件是在用户前期开发结束后,通过集成开发工具生成的用于配置FPGA芯片中可重构资源的二进制文件[21].FPGA配置时需要将配置文件从本地开发环境(运行在PC或工作站上的EDA软件),或外部存储系统传输到FPGA内部存储空间,然后再由内部控制器进行配置控制.对配置文件压缩处理可以减少外部传输时间,提高配置速率.本节首先对可重构系统配置过程进行详细介绍;然后针对动态可重构系统特征与要求,结合行程编码压缩算法探索多位压缩元配置文件最优压缩参数;然后对压缩文件进行深入分析,对行程编码压缩算法进行改善,最终实现二进制配置文件高效压缩.
2.1 可重构系统配置流程
本节首先从整体上介绍FPGA动态可重构系统的通用配置模型,然后通过Xilinx Virtex -Ⅱ系列FPGA的配置模型详细介绍配置过程[10],Virtex -Ⅱ系列FPGA为Xilinx 高端FPGA的入门级产品,其硬件结构最具有代表性,最后以该模型为基础,对动态可重构系统的配置时间代价进行分析,提出优化配置时间方案.
图4为动态可重构系统的通用配置模型图,主要由内外2部分组成.外部主要由非易失性存储器与存储控制器组成,非易失性存储器存储配置文件,存储控制器控制片外存储器的工作.内部FPGA部分主要由配置控制器、片内高速缓存、配置端口以及配置单元存储区组成.传统的配置控制器和配置端口协议均由软核IP实现,目前FPGA为了减少系统配置时间,这2部分采用硬件实现并集成在FPGA芯片中[22].片内高速缓存的核心作用是存储从片外高速存储器传输的配置数据,配置控制器与片内高速缓存通信,将配置数据发送给配置端口.配置控制器也与配置端口通信,当配置端口内部缓冲区饱和时,配置控制器控制片内高速缓存停止向配置端口发送数据.配置端口将配置信息传送至相应的可重构单元配置存储区,实现可重构单元逻辑功能.
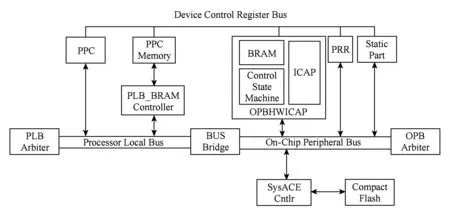
Fig. 5 Virtex -Ⅱ series PPGA dynamic reconfigurable system图5 Virtex -Ⅱ系列PPGA动态可重构系统配置
动态可重构系统配置过程可以被划分为2个阶段:1)通过片外存控制器进行配置数据下载,他控制片外高速存储器将配置数据传输给片内高速缓存;2)为配置控制器将高速缓存区配置数据通过配置端口加载至可重构单元配置存储区.2部分以流水线方式同时运行,直至配置文件被全部传输至配置单元存储区或者第1阶段全部配置数据被传输至片内高速缓存.配置过程中2个阶段是分离的,第1阶段可以在第2阶段开始前将全部配置数据下载至片内高速缓存(在片内缓存容量充足前提下),提高系统配置速率.
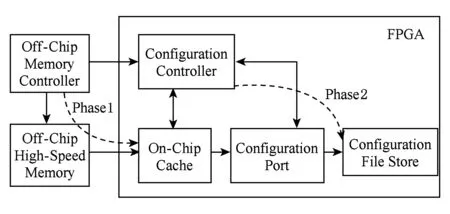
Fig. 4 General configuration model of dynamic reconfigurable system图4 动态可重构系统通用配置模型
图5为Xilinx Virtex -Ⅱ系列FPGA动态可重构系统配置图[23].灰色部分为FPGA外围设备,白色部分为FPGA内部结构. PPC(PowerPC)为嵌入式处理器,控制整个配置流程,其功能也可使用软核嵌入式处理器Microblaze实现.PLB_BRAM controller分别与PLB总线与PPC Memory相连,控制双方数据传输.OPBHWICAP是一种配置协议控制器[24],他采用有限状态机控制ICAP对动态可重构区域(partially reconfigurable regions, PRR)与静态区域(static part)进行配置.OPBHWICAP中的BRAM为配置缓冲区,一般由FPGA内部BRAM组成,大小为2KB. SysACEcntlr( system advanced configuration environment controller)是Xilinx提供的高级配置环境,实现外部微型存储器(compact flash,CF)与内部总线之间的高速通信[25].FPGA重构配置过程可划分为3个阶段(如图5所示):
1) PPC向System ACE cntlr发出指令,将外部存储器中配置数据以块(block)为单位传输至FPGA内部存储器PPC Memory.
2) PPC控制PLB_BRAM controller将配置数据以字(word)为单位传输至ICAP配置缓存器BRAM.
3) 当ICAP配置缓存器饱和时,PPC控制OPBHWICAP将配置数据通过ICAP加载至可重构单元配置存储区.
3个阶段以流水线方式执行,直到配置文件全部加载到配置存储区,配置过程结束[26].
根据上述配置过程描述,FPGA配置过程3个阶段可被简化为EM-PPC,PPC-ICAP,ICAP-CM,其中EM(external memory)为外部存储器,RT(reconfigure time)表示可重构系统配置时间:
RT=RTEM-PPC+RTPPC-ICAP+RTICAP-CM,
(1)
其中,RTEM-PPC,RTPPC-ICAP,RTICAP-CM分别表示配置阶段EM-PPC,PPC-ICAP,ICAP-CM所需时间.文献[24]对3个阶段占据整个配置时间的比例进行统计,结果如表1所示:
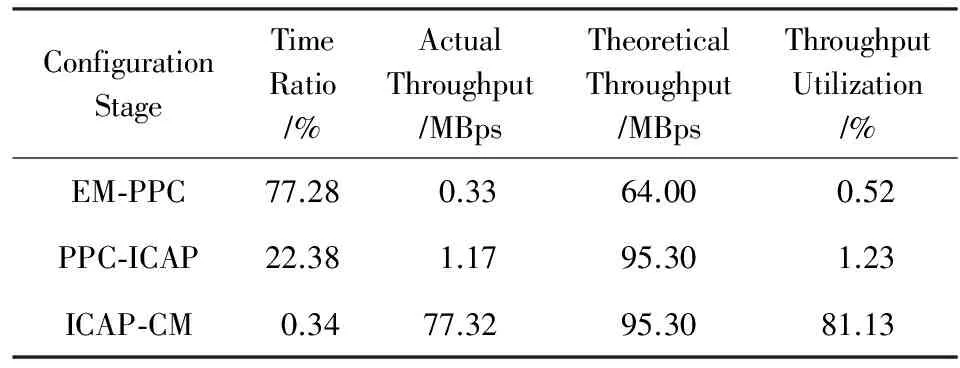
Table 1 Statistics of Configuration Time Ratio, Port Throughput and Theoretical Throughput
表1中的外部存储器为CF卡.从表1可知:1)EM-PPC阶段时间代价最高,约占可重构配置时间的77.28%;2)EM-PPC阶段吞吐量利用率最低,仅占理论吞吐量的0.52%.由表1可得,对EM-PPC配置阶段进行优化,可大幅度提高配置速率,依据Amdahl定律:

(2)
其中,P为EM-PPC所占时间百分比,S为该阶段优化时间加速比,满足S≥1.
可以采用2种思路对该阶段传输速率进行优化:1)提高吞吐量;2)压缩配置文件.表1中采用CF卡的最大传输速率为64 MBps,若将配置文件提前传输到DDR2@ 800 MBps高速存储器中,则EM-PPC加速比S=12.5,对应的Speedup=3.46,即配置时间减少到原始配置时间的28.9%.如将配置文件压缩为原始配置文件大小的50%,则配置时间减少到原始配置时间的72.72%.本文旨在不修改硬件结构的前提下,对通用动态可重构系统配置时间进行优化,本文选用配置文件压缩思想进行配置时间优化.
2.2 RLE配置文件压缩算法
通过对动态可重构系统配置过程分析,本文选用压缩配置文件思路减少系统配置时间.通过对国内外研究现状分析,本文根据2级制配置文件的特征,采用行程编码无损压缩算法RLE进行配置文件压缩.本节首先对RLE压缩算法进行介绍.其次依据benchmark中二进制配置文件特征选择RLE压缩算法参数.然后对定长RLE压缩算法结果进行分析,结合Huffman编码思想实现变长RLE压缩算法.最后,根据变长RLE压缩结果中“0”“1”分布规律,采用掩码压缩思想实行2次压缩,实现掩码变长RLE压缩算法.
RLE压缩算法是一种简单高效的无损压缩算法,该算法将压缩信息视为字符串序列,核心思想是将字符串序列中连续相同字符统计表示,实现文本压缩目标.对于连续相同字符采用字符加计数方式进行表示,对于不重复字符,计数为1.RLE压缩结果可采用元组(C,L)表示,C为被压缩字符,L为计数.例如字符串“AAAAABBCCCCD”经过压缩后,结果为“A5B2C4D1”.本文将RLE压缩算法移植到对二进制配置文件的压缩,字符串序列转换为位序列,压缩单位由字节转换为位.不同于字符串压缩,二进制文件压缩结果中C与L使用二进制表示.如位序列“11111100011111000000”经过压缩后的中间结果为“16031506”,然后将计数L采用二进制表示,结果为“111001111010110.序列压缩前长度为20 b,压缩后位长度为15 b,实现压缩的目的.在解压过程中,由于C与L均为二进制表示,无明确分界点,解压失败.解决思路有2种:1)采用压缩标记位的定长压缩表示格式,如图6(a)所示;2)采用无压缩标记位的定长压缩表示格式,如图6(b)所示.

Fig. 6 RLE binary compressed format图6 RLE二进制压缩表示格式
本文采用带标记位的定长压缩表示方法,减少未重复数据带来的计数位长度代价,本文后续所指定长压缩均为带标记位的定长压缩.采用定长压缩方法得到的压缩率的取值范围:
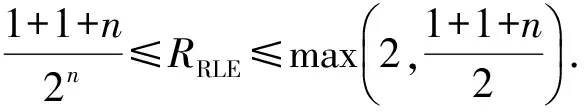
(3)
其中,m∈+,n∈+.此时,压缩率RRLE的取值范围:
(4)
同样,在最糟糕的情况下仍然会出现压缩膨胀.
定长RLE压缩算法中的压缩元C长度m与计数L长度n可根据配置文件特征进行选择,追求最小压缩率.本节以Xilinx 系列FPGA配置文件为代表,对配置文件的分类和组成进行相关介绍,对benchmark中重复数据进行分析,采用理论结合实验的方式来确定最优m,n组合.
Xilinx FPGA应用程序开发工具(ISE和Vivado)可以按照需求不同生成5种格式配置文件,对应后缀名分别为:bit,rbt,bin,mcs,hex,不同配置文件对应不同配置环境.bit文件包含配置文件组成中的所有部分:冗余头部信息、配置信息、CRC校验信息和冗余尾部信息.冗余头部信息主要包括当前工程名称、芯片型号和编译时间等信息,由于工程名长度不定,一般头部信息长度约为72 B.配置信息为配置文件的主体部分,进行可重构计算单元、路由单元以及存储单元的信息配置.校验信息对配置信息进行校验.冗余尾部信息由12个32 b的空操作组成,这部分不会被加载到FPGA中,目的是给予配置器充足的时间完成配置过程.本文以.bit格式配置文件为原始数据进行二进制配置文件压缩研究.
图8为Xilinx Kintex-7 XC7K325T 芯片部分二进制配置文件片段[2](16进制表示、Xilinx官网提供).FPGA配置以帧为最小配置单位,每帧大小为32 b.从图8中可以得出2个结论:1)配置帧帧内存在大量的重复数据;2)配置帧帧间也存在大量重复数据.根据配置帧长度和帧内重复的特征,本文拟给压缩元长度m分别赋值为1,2,4,8,16,32.依据压缩元连续出现的频数计算获取相应的计数L长度n值,从中选出1组理论压缩率最低的(m,n)元组作为定长压缩参数.本文采用理论结合实验的方法选取最优参数组合,实验数据为V5_DES56.bit.压缩率RREL计算为
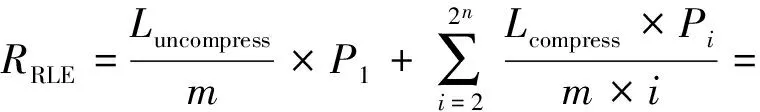
(5)
其中,Luncompress为未压缩表示格式长度,Lcompress为压缩表示格式长度.

Fig. 8 Kintex-7 XC7K325T binary configuration file图8 Kintex-7 XC7K325T 二进制配置文件片段
当m=1时,不需要对配置文件做任何处理,直接统计压缩元(0或1)在不同计数L下的重复频数,并计算对应配置数据占配置文件大小百分比.当压缩元重复频数大于计数L可表示范围时,采用截断方法处理.如当n=8时,可表示的最大数值为256,当统计频数大于256时,采取截断处理,重新压缩.因为不会出现计数L=0的情况,所以本文采用(L-1)对应的二进制数表示计数L.如连续260个“1”被压缩为(1,1,11111111)(1,1,00101011).当m=1,n=8时,统计结果如表2所示.
当m=1,n=8,压缩标记为“0”时,压缩格式长度为2;压缩标记为“1”时,压缩格式长度为10.此时理论压缩率:
(6)
其中,Pi为L=i对应配置数据大小占据配置文件百分比.将表中相关数据带入式(6),计算可得RRLE值为109.42%,即采m=1,n=8元组时,理论压缩率为109.42%,出现压缩膨胀现象.究其原因,主要是因为当n=8时,压缩格式长度为10,若原始数据连续长度小于10的重复数据均会产生压缩膨胀现象,而此部分所占比例为38.41%,膨胀部分占据比例过高.后续需要将n值减小,降低膨胀部分所占比例.当n值分别取3,4,5,6,7时对应的压缩率如表3所示.

Table 2 Statistics of Corresponding Data (m=1,n=8)表2 m=1,n=8对应数据统计表

Table 3 Different n Value Compression Rate (m=1)表3 m=1对应不同n值压缩率表
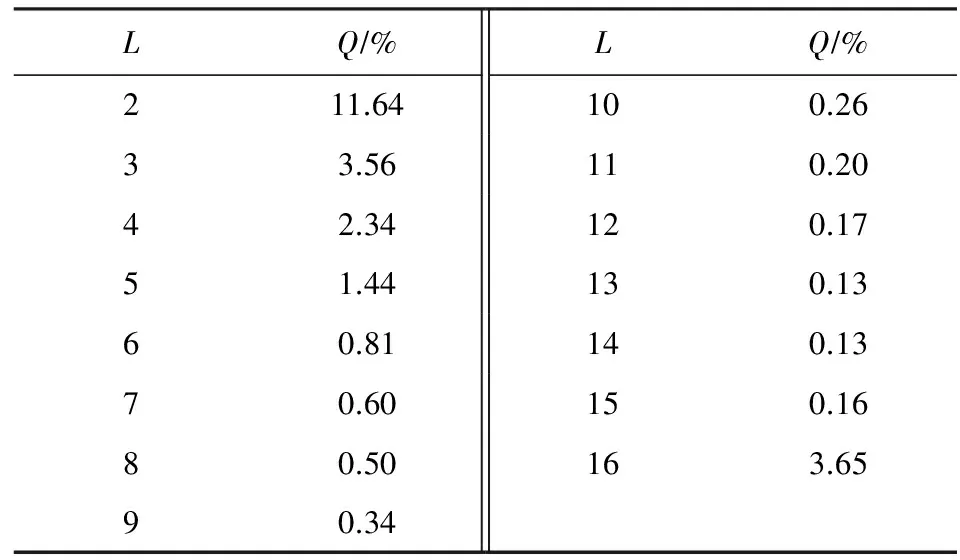
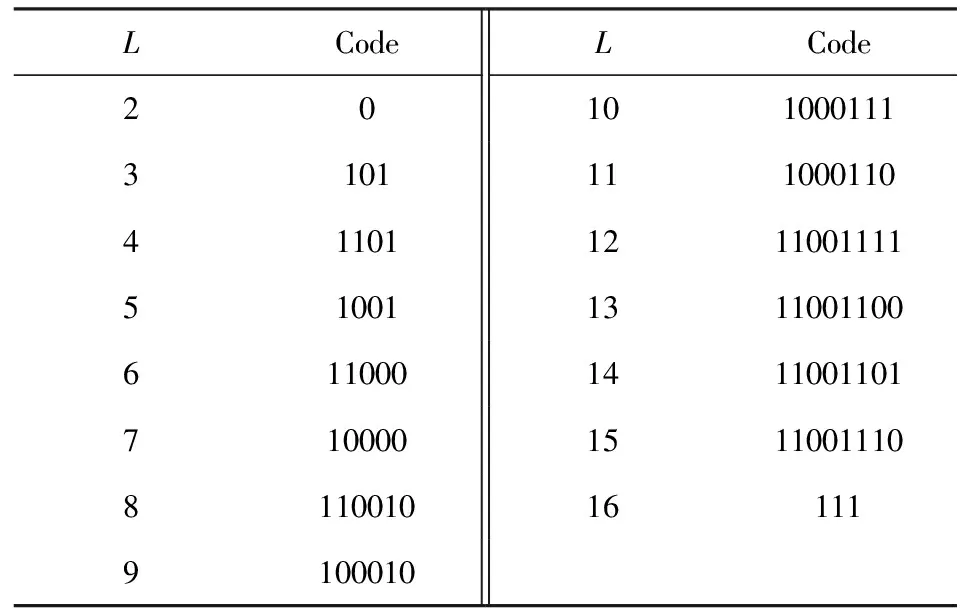
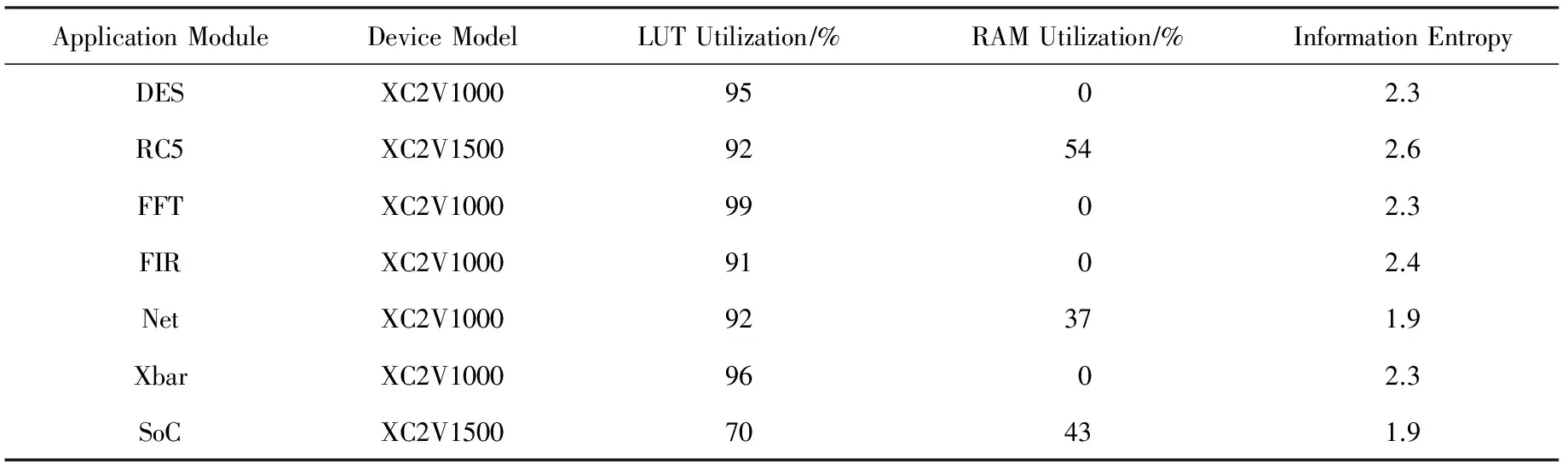
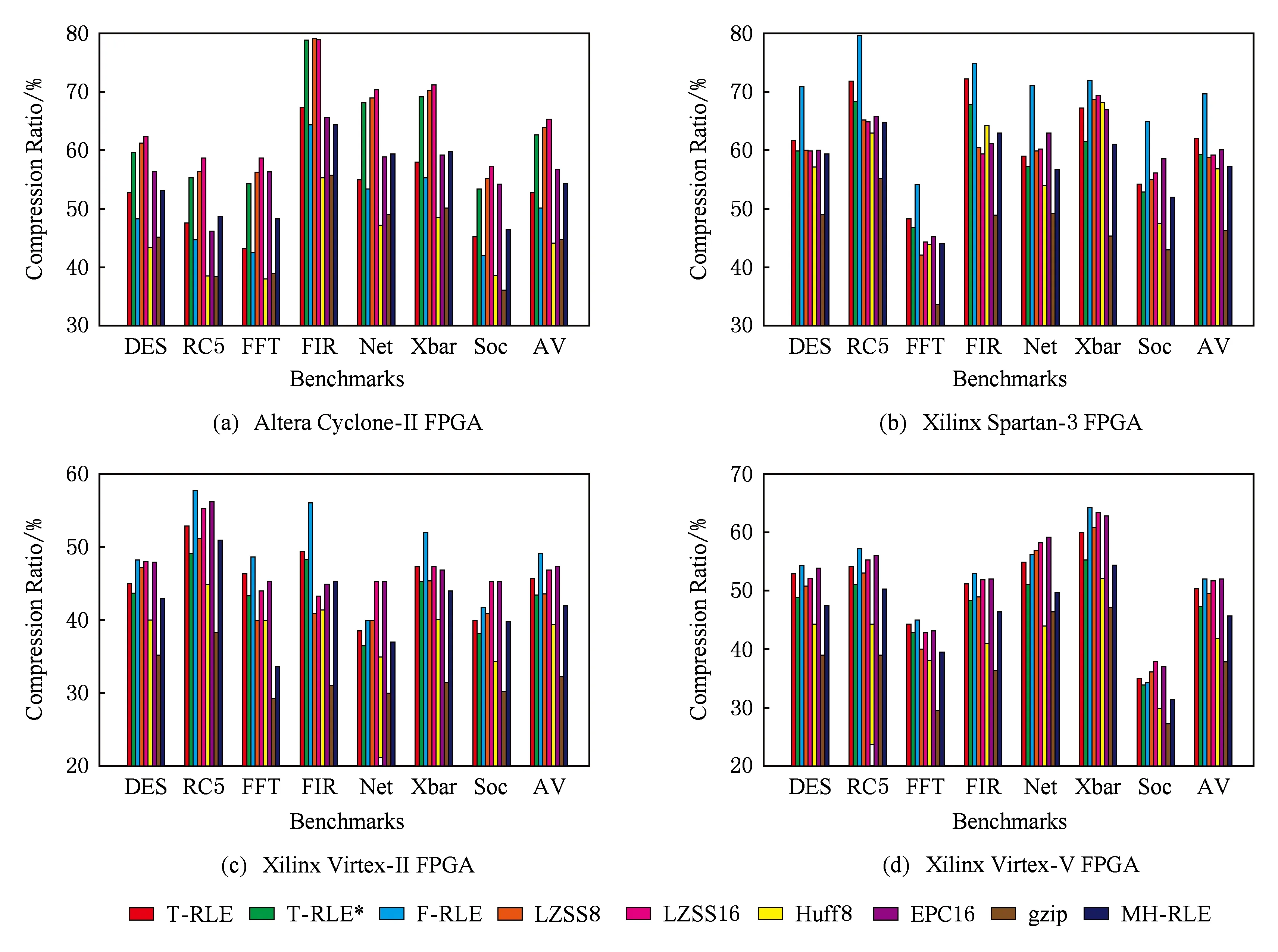
从上述计算结果可知,当压缩元C长度m=1时,计数L长度n=5时压缩率最低,压缩效果最好.当n=1或者n=2时,附加压缩标记位,在任何情况下都是压缩膨胀.同样,随着n值越来越大,压缩格式长度n+2值也会增大,计数L 同理,计算当m分别为2,4,8,16,32,n分别为1~10时的压缩率并进行汇总,当m分别为2,4,8,16,32时的最佳压缩率如表4所示: Table 4 The Optimal (m,n) Compression Ratio Statistics表4 最优(m,n)元组压缩率统计表 由上述理论计算结果可知,当m=4,n=4时定长RLE压缩算法取得最优压缩效果.本文后续将m=4作为通用二进制配置文件的最佳压缩元长度向变长RLE压缩算法进行改善,进一步降低压缩率. 定长RLE压缩格式后n位为计数长度,可以表示计数范围为[1,2n].当采用定长压缩方案m=4,n=4时,计数L=2的二进制表示为“0001”,其中前3个“0”起到占位作用.当计数L=3或4时,前2个“0”起到占位作用,他们的存在与否并不会对计数值产生影响,只是起到辅助解压的作用.根据统计结果可以预测,当计数长度为n,计数L∈[2,2n-1]占据配置文件比例远高于L∈[2n-1+1,2n],并且对于同一个m值,随着n值增大,前半部分占据的比例会越来越高.L∈[2,2n-1]时,计数格式都会存在占位“0”,若可以将占位“0”删除掉,会对压缩效果产生明显改善,降低压缩率. 定长RLE压缩格式的优势在于解压缩简单,只需按照相应标记位长度、压缩元长度m和计数长度n进行解释实现解压过程.例如,当m=4,n=4时的压缩数据如图9(a)所示,按照定长RLE压缩算法,对应的解压数据如图9(b)所示.如果将压缩数据中的占位“0”删除,则压缩数据如图9(c)所示.解压时,前1个压缩格式中的计数长度不能确定,前1个压缩格式中的计数部分与后1个压缩格式中的压缩标记位甚至压缩元重合(图9(c)阴影部分),无法正确解压.如果可以动态识别计数部分长度,如图9(d)所示,就可在不增加附加信息的前提下正确解压.本文采用Huffmam编码方式对计数部分进行编码,解决动态识别计数部分长度问题. Fig. 9 Compression and decompression图9 RLE压缩与解压缩示意图 Huffman编码是David Huffman于1952年提出的一种变长信息编码方式.Huffman编码首先统计编码字符在文件中出现的频率.依据统计信息构建一棵二叉树,该二叉树又被称为Huffman树.通过Huffman树为每个字符提供唯一的二进制编码.将编码文件中的每个字符用对应的二进制编码替换,得到编码文件.Huffman编码核心思想是将出现频率高的字符用较短的二进制表示,出现频率低的字符用较长的二进制表示,保证编码文件最小.Huffman编码又被称为最优前缀编码,因为Huffman树确保每个字符对应的二进制编码都不会是其他二进制编码的前缀.本文利用Huffman编码的带权路径最短与前缀性解决RLE压缩格式中计数部分长度动态识别问题,提出变长Huffman Run Length Encoding (H-RLE)压缩算法.通过m=4,n=4的统计结果介绍H-RLE压缩思想.当m=4,n=4时,计数L不同长度出现次数的概率Q如表5所示: Table 5 Frequency of Different L表5 不同L对应频率统计表 然后依据Huffman编码算法对2~16分别编码,结果如表6所示: Table 6 Huffman of Different L表6 不同L对应Huffman编码 然后根据式(7)计算理论压缩率: (7) 其中,|C(i)|表示计数重复次数i对应的编码位数.将相关数据带入计算式得出RRLE为58.76%,计算结果表明,采用Huffman编码表示计数部分可以降低压缩率. H-RLE跳出了定长RLE压缩算法计数部分n位限制,消除了占位“0”,降低了压缩率.上述示例中重复数据出现频数被限制在了L∈[1,16](n=4).依据m=4,n=8的统计结果可知,L=256出现的频数为1586,占据整个配置文件的19.4%.按照上述压缩表示方式,连续256个压缩元被划分为16(256/16)个L=16的8 b长度压缩格式,压缩后的长度为128 b,该部分压缩率为12.5%.如果可以将L=256进行Huffman编码(假设256对应的Huffman编码长度为20 b),那么该部分的压缩率就可达到2.44%.本文综合考虑Huffman编码长度与配置文件统计结果选择最大L值.当L=512时出现的频率为973,占据整个配置文件的23.8%;当L=1024时出现的频率为458,占据整个配置文件的22.4%;当L=2048时出现的频率为212,占据整个配置文件的20.74%;当L=4096时出现的频率为78,占据整个配置文件的15.26%.假设当L=2048时对应的Huffman编码长度为25 b,该部分的压缩率可达到0.37%;当L=4096时对应的编码长度为26 b,该部分对应的压缩率为0.19%,相对于L=2048,文件整体压缩率降约低了0.18%,改善不大.本文选择最大L=2048,并根据此数据对测试文件进行重新统计,获取较优Huffman编码.表7给出L为部分数值时对应频率: Table 7 Frequency of Extended L表7 扩展的L值对应频率统计表 对应的Huffman编码如表8所示: Table 8 Huffman Coding of Extended L表8 扩展的L值对应Huffman编码 当计数L>2 048时,按照截断方法处理.从表8可知,当L>16时并没有采用等差增长的方式进行统计,而是采用了公比为2的等比增长方式统计.假如按照等差增长方式,编码位数增长较快,当L=2 048时,需要上千位编码表示.采用公比为2的等比增长方式有2个优势:1)随着L值的等比增长,编码位数增加缓慢,减少编码长度,降低压缩率;2)当统计数据不属于编码数据中的某一数值时,可采用较少次数的截断方法表示该数据(类似于二分查找思想).例如当统计次数为448时,可以采用256-128-64这种2次截断3个压缩格式的方式表示,表示长度为48 b.如果不存在L=64 b和L=128 b对应的Huffman编码,需要采用256-32-32-32-32-32-32这种6次截断7个压缩格式表示,表示长度为100 b.L∈[2,16]采用等差增长是因为该部分所占频率占据了[2,2 048]中的99.3%,若采用截断方式,会增加表示长度.本文根据统计结果以及编码方式,将L≤2 048中未编码的值采用截断处理,然后计算理论压缩率: (8) 其中,S为经过编码处理的L值集合.将相应的数据带入式(8)可得其压缩率为53.43%. 按照H-RLE压缩算法对测试文件进行压缩,理论计算得到的最小压缩率为53.43%.其中包含未压缩部分的40.93%与压缩部分的12.50%.从式(8)可以得出2点结论:1)原始文件中未压缩部分P1占据32.74%,这部分导致压缩率RREL>40.93%;2)其余67.26%部分被压缩至12.50%,表明配置文件中连续重复的“0”或者“1”较多,“0”,“1”分布并不均匀.由结论1可知,如果不对未压缩部分进行处理,压缩率将不会产生明显改善.本文后续对H-RLE压缩结果进行分析,依据分析结果采用掩码压缩思想,提出Mask Huffman Run Length Encoding (MH-RLE)压缩算法进行2次压缩,进一步降低压缩率,提升压缩效果. 掩码压缩最初提出主要是为了优化静态字典压缩算法,采用掩码的方法,提高字典的覆盖范围.在静态字典压缩算法中,需要将原始数据与字典条目进行匹配,若匹配成功,用该条目在字典中的位置表示该数据.在二进制静态字典压缩过程中会存在许多数据与字典中数据仅相差n位,这样的数据不能被压缩.将这些数据与字典中的某1条目进行异或操作,可以得出n个差异位置.由于异或操作具有可逆性,解压时只需将对应位置的“0”修改为“1”,然后与字典数据进行异或运算.例如假设字典条目为“01000100”,原始数据为“01000000”,异或结果为“00000100”,即数据不同位为第5位.解压时只需将“00000000”中第5位修改为1,然后字典条目“01000100”进行异或运算,得出结果为原始数据“01000000”. 本文根据原始文件“0”,“1”分布不均匀的特征,对压缩后的文件进行统计分析,得出“0”占据变长RLE压缩后文件的21.14%,“1”占据 78.86%.根据“0”,“1”分别所占比例,本文以5 b为单位长度,以1 b为掩码长度进行掩码压缩,压缩格式如图10所示: Fig. 10 Mask format图10 掩码格式 掩码标识为“0”表示5 b原始数据未被处理,即5 b原始数据与“00000”进行异或运算,得出结果中含有“1”的数量count≥2.掩码标识为“1”表示异或运算结果中含有“1”数量为0或1.3 b数据表示“1”出现位置,即“001”至“101”表示“1”从左至右出现的位置.本文用“000”表示5 b原始数据为“00000”,用“111”表示5 b原始数据为“11111”.由于配置文件是以配置帧为单位进行配置,而配置帧的大小为32 b,非5的整数倍,本文对于剩余位数采取掩码为“0”的非压缩处理并且不采用补位处理,保证后续配置过程的正确性. 当掩码格式确定后,本文对H-RLE压缩后的结果进行重新处理,实现MH-RLE压缩算法:1)对每5 b数据与“00000”进行异或运算;2)统计运算结果中“1”的数量count,当count≥2,输出0,count≥1时输出为1;3)统计输出结果中0和1所占百分比.根据处理结果可知,0所占百分比为27.21%,1所占百分比为 72.79%.然后计算理论压缩率: (9) 其中,RREL_MASK表示MH-RLE压缩率.将上述统计结果以及RREL=53.43%带入式(9),计算理论压缩率为48.56%. 可重构系统配置文件压缩过程在集成开发环境中通过软件压缩算法实现,压缩时间代价对动态可重构系统配置性能没有影响.本节不考虑压缩时间,仅从压缩率角度评价本文提出的MH-RLE压缩算法性能.本节首先对测试数据集中的二进制配置文件进行简单介绍,然后通过本文提出的压缩算法对所有测试文件进行压缩,最后将压缩结果与多种优秀的压缩算法的压缩结果进行对比,评价本文压缩算法的优劣. 本次实验测试数据集来源于Department of Computer Science 12[27].为了保证压缩算法对不同应用程序的有效性,测试集包含了3种FPGA应用领域程序模块,其中包括加密模块DES和RC5、信号处理模块FFT与FIR、网络通信模块Net(network router)与Xbar (crossbar).上述6种应用程序占据LUT资源90%以上.测试集增加了SoC模块配置文件,占据LUT资源70%左右,确保在不同资源利用率下的压缩算法性能.为了体现压缩算法对各种FPGA芯片对应配置文件压缩效果,测试数据分别由2个生产商的4个系列FPGA芯片组成,分别为:Altera Cyclone -Ⅱ,Xilinx Spartan-3,Xilinx Virtex -Ⅱ,Xilinx Virtex-V.表9~12介绍各种应用模块在不同FPGA芯片上对应可重构资源利用比例信息. Table 9 Resources Using Rate of 7 Applications in Altera Cyclone -Ⅱ Table 10 Resources Using Rate of 7 Applications in Xilinx Spartan-3 Table 11 Resources Using Rate of 7 Applications in Xilinx Virtex -Ⅱ Table 12 Resources Using Rate of 7 Applications in Xilinx Virtex-V 图11为9种压缩算法分别在4个系列FPGA芯片测试环境下的压缩率比较图.9种压缩算法分别为T-RLE,T-RLE*,F-RLE,LZSS8,LZSS16,HUFF8,EPC16,GZIP和本文提出的MH-RLE.其中HUFF8为Huffman压缩算法的实现,之中的8表示以8b为单位建立Huffman树.GZIP为Linux环境下常用压缩程序,实验中使用的GZIP版本为1.3.5.为了忽略各种压缩算法对个别配置文件具有较低压缩率,实验采用均值(AV)比较各个压缩算法的性能(图11中每幅图的最右边类别).从图11中可以看出,各种压缩算法对不同配置文件的压缩性能表现各不一样,不能依据某1组实验结果确定某个压缩算法的性能,本节主要参考AV值来分析MH-RLE压缩算法性能.MH-RLE在Altera Cyclone -Ⅱ,Xilinx Spartan-3,Virtex -Ⅱ,Virtex-V FPGA芯片的平均压缩率分别为:54.36%,57.32%,41.98%,45.61%. 首先,从图11可得,MH-RLE压缩率高于HUFF8与GZIP.在二进制配置文件压缩算法中,Huffman算法首先将配置信息全部遍历,然后根据指定压缩元长度统计压缩元频数,建立相应的静态Huffman树,最后依据Huffman树进行压缩,也可以在第1次变量过程中动态建立Huffman树.Huffman压缩算法具有较优的压缩率,但是解压硬件资源消耗过大.配置文件解压过程需要由硬件完成,Huffman解压过程需要将Huffman树存入硬件资源,需要耗费大量的硬件资源,Huffman解压所需硬件资源为其他压缩算法对应解压资源的40倍左右.GZIP核心思想是通过LZSS压缩算法的变形算法对配置文件进行首次压缩,然后将压缩结果采用Huffman压缩算法进行2次压缩,所以GZIP压缩算法虽然具有较优的压缩率,但是解压缩硬件代价比Huffman压缩代价更高,在可重构系统中一般不会采用GZIP压缩算法.MH-RLE压缩算法虽然也采用了Huffman压缩思想,但是Huffman树对应的叶子节点仅有22个,并且静态建立,即该Huffman树对所有配置文件压缩与解压均有效,不会因为配置文件不同而重新修改解压算法的实现. Fig. 11 Compression ratio comparison图11 压缩率比较图 其次,相对于Xilinx系列FPGA对应配置文件,在Altera系列FPGA对应配置文件中,MH-RLE压缩算法性能明显下降.图11(a)中MH-RLE压缩算法压缩率比T-RLE*,LZSS8,LZSS16,EPC16压缩算法压缩率低,比T-RLE和F-RLE压缩算法压缩率高.在图11(b)~(d)中,MH-RLE压缩率仅高于HUFF8和GZIP压缩算法,主要原因是MH-RLE压缩算法中的所有参数均来源于对Xilinx系列FPGA配置文件数据的统计,而Altera系列对应的配置文件描述方式(非公开)与Xilinx系列有所不同,所以MH-RLE压缩算法针对Altera系列FPGA配置文件的压缩性能不如Xilinx系列FPGA配置文件. 最后,本节通过具体数据表现MH-RLE压缩算法相对于其他8种压缩算法压缩率降低比例,数据计算方式为RMH-RLE-Rother,计算结果如表13所示,其中,“-”表示压缩率降低. Table 13 Comparison of Compression Ratio Optimization表13 MH-RLE压缩率优化比较表 % 根据本文提出的FPGA配置文件压缩算法,进行相应的硬件解压缩电路设计,由于配置文件是以1帧二进制数据(32 b)的形式进行数据存储和传输,因此,结合MH-RLE压缩算法的特点,将解压电路设计为外部、内部2个部分,其中解压缩外部电路如图12所示,由队列缓存(queue buffer)、输入缓存(input buffer)、解压缩模块(MH-RLE decoder)、输出缓存(output buffer)组成,其中队列缓存按配置帧缓存被压缩后的配置文件数据,输入缓存以配置帧为单位依次从队列缓存中抽取数据,解压缩模块实现MH-RLE解压缩算法,输出缓存放置原始配置文件数据,等待后续电路读取. 图13为解压缩内部电路实现,开发工具为XILINX ISE Design Suite 13.4,开发语言为VHDL,以解压缩模块的顶层电路设计图形式进行展示.其中InputBuffer用于接收1帧(32b)二进制数据,Judgment判断是否进行了掩码压缩和Huffman压缩,根据判断结果通过使能信号(EN)调用Mask或Huffman进行相应的解压缩实现,由于本文的压缩算法为2次压缩,因此需要Mbuffer对中间数据进行暂存,OutputBuffer进行解压后的数据存储. Fig. 12 External decode circuit图12 解压缩外部电路 Fig. 13 Internal decode circuit图13 解压缩内部电路 将上述解压缩电路与文献[28-29]中的解压缩电路进行硬件资源使用量对比,文献[28]采用了掩码压缩与Huffman编码相结合的方式实现压缩算法,其解压电路所需的Slice数量为250个,针对Huffman编码的解压电路需要将整个Huffman树存入硬件,从而耗费大量的硬件资源,本文提出的MH-RLE压缩算法对Huffman压缩进行了改进,解压电路所需Slice只占到其解压电路所需Slice的1/3(84个).而与传统的基于LZSS压缩算法的解压缩电路实现[29]占用45个Slice相比,MH-RLE解压电路所需硬件略高,但是为了提高压缩比,减少数据传输时间,在现有的硬件资源相对充足的前提下,以牺牲少许资源为代价来得到更快的运行速率是值得的. 本文以RLE压缩算法为基础,提出MH-RLE配置文件压缩算法.首先,针对优化定长RLE压缩算法的性能,本文采用统计方式对测试文件进行统计,以理论计算的方式选择出最优的压缩元长度m与计数长度n.然后,针对定长压缩算法计数部分“0”占位的缺憾,采用Huffman编码方式对计数表示部分进行编码,实现变长H-RLE压缩算法.本文依据压缩元连续分布信息,选取22个编码单位并进行Huffman编码,该方式的优势在提高压缩率的前提下,减少解压缩硬件消耗代价.对H-RLE压缩后的数据进行分析,采用掩码压缩思想进行2次压缩,实现了最终的配置文件压缩算法MH-RLE.仿真实验表明,MH-RLE压缩算法相对于大多数配置文件压缩算法均有较好的压缩性能,并且更适合于Xilinx系列FPGA配置文件压缩.MH-RLE的平均压缩率为49.82%,相较于其他6种压缩算法均有不同程度的提升,最多可提升12.4%.后续研究可以针对Altera系列FPGA重新设计MH-RLE压缩算法参数,使得该算法可以对Altera系列FPGA配置文集也有较低的压缩效率. [1]Xilinx Inc. Expanding the all programmable SoC portfolio[EB/OL]. [2016-05-21]. http://www.xilinx.com/products/silicon-devices/soc/zynq-7000/silicon-devices/index.htm [2]Xilinx Inc. 7 series FPGAs configurable logic block user guide,version1.8: Userguide[EB/OL].[2016-05-21]. http://china.xilinx.com/support/documentation/user_guides/ug474_7Series_CLB.pdf [3]Altera Corporation. Configuration, design security, and remote system Upgrades in ArriaII devices[EB/OL]. 2012-07 [2016-05-21]. https://www.altera.com/content/dam/altera-www/global/en_US/pdfs/literature/hb/arria-ii-gx/aiigx_51009.pdf [4]Vliegen J, Mentcns N, Verbauwhede I. A single-chip solution for the secure remote configuration of FPGAs using bitstream compression[C] //Proc of the 8th IEEE ReConFig. Piscataway, NJ: IEEE, 2013 [5]Tefan R. Bitstream compression techniques for Virtex 4 FPGAs[C] //Proc of the 18th IEEE FPL. Piscataway, NJ: IEEE, 2008: 323-328 [6]Tajammul M A, Jafri S M A H, Hemani A, et al. Private configuration environments (PCE) for efficient reconfi-guration, in CGRAs[C] //Proc of the 24th IEEE ASAP. Piscataway, NJ: IEEE, 2013: 227-236 [7]Inoue H, Yamada J, Yoneda H, et al. Test compression for dynamically reconfigurable processors[J]. ACM Trans on Reconfigurable Technology and Systems, 2011, 4(4): 205-210 [8]Jia Rui, Wang Fei, Chen Rui, et al. JTAG-based bitstream compression for FPGA configuration[C] //Proc of the 11th IEEE Int Conf on Solid-State and Integrated Circuit Technology. Piscataway, NJ: IEEE, 2012 [9]Wu Weiguo, Yang Zhihua, Yu Guoliang. A reconfigurable configuration compression algorithm based on contextually adaptive arithmetic coding[J]. High Technology Letters, 2011, 21(5): 443-450 (in Chinese) (伍卫国, 杨志华, 余国良. 基于上下文自适应算术编码的可重构配置信息压缩算法[J]. 高技术通信, 2011, 21(5): 443-450) [10]Duhem F, Muller F, Lorenzini P. Reconfiguration time overhead on field programmable gate arrays: Reduction and cost model[J]. LET Computers & Digital Techniques, 2012, 6(2): 105-113 [11]Abdelhadi A, Lemieux G G F. Configuration bitstream reduction for SRAM-based FPGAs by enumerating LUT input permutations[C] //Proc of the 6th IEEE ReConFig. Piscataway, NJ: IEEE, 2011: 20-26 [12]Jafri S M A H, Hemani A, Paul K, et al. Compression based efficient and agile configuration mechanism for coarse grained reconfigurable architectures[C] //Proc of the 2nd IEEE IPDPSW. Piscataway, NJ: IEEE, 2011: 290-293 [13]Qin Xiaoke, Muthry C, Mishra P. Decoding-aware compression of FPGA bitstreams[J]. IEEE Trans on Very Large Scale Integration (VLSI) Systems, 2011, 19(3): 411-419 [14]Nabina A, Nuńez-Yańez J L. Dynamic reconfiguration optimisation with streaming data decompression[C] //Proc of the 20th IEEE FPL. Piscataway, NJ: IEEE, 2010: 602-607 [15]Jordan M C, Vaidyanathan R. MU-decoders: A class of fast and efficient configurable decoders[C] //Proc of the 1st IEEE Int Symp on Parallel & Distributed. Processing. Piscataway, NJ: IEEE, 2010 [16]Liu Bo, Zhu Wanyu, Liu Yang, et al. A configuration compression approach for coarse-grain reconfigurable architecture for radar signal processing[C] //Proc of the 6th IEEE Int Conf on Cyber-Enabled Distributed Computing and Knowledge Discovery. Piscataway, NJ: IEEE, 2014: 448-453 [17]Sellers B, Heiner J, Wirthlin M, et al. Bitstream compression through frame removal and partial reconfiguration[C] //Proc of the 19th Int Conf on Field Programmable Logic and Applications. Piscataway, NJ: IEEE, 2009: 476-480 [18]Gu Haiyun, Chen Shurong. Partial reconfiguration bitstream compression for Virtex FPGAs[C] //Proc of the 1st IEEE Image and Signal Processing. Piscataway, NJ: IEEE, 2008: 183-185 [19]Beckhoff C, Koch D, Torresen J. Portable module relocation and bitstream compression for Xilinx FPGAs[C] //Proc of the 24th IEEE Int Conf on Field Programmable Logic and Applications. Piscataway, NJ: IEEE, 2014 [20]Jing Xie, Wang Yabin, Chen Liguang, et al. Fast configuration architecture of FPGA suitable for bitstream compression[C] //Proc of the 8th IEEE ASICON. Piscataway, NJ: IEEE, 2009: 126-130 [21]Xu Wenbo, Tian Geng, Xilinx FPGA: Development and Application[M]. 2nd ed. Beijing: Tsinghua University Press, 2012: 85-102 (in Chinese) (徐文波, 田耘. Xilinx FPGA开发实用教程[M]. 2版. 北京: 清华大学出版社, 2012: 85-102) [22]Delorme J, Nafkha A, Leray P, et al. New OPBHWICAP interface for realtime Partial reconfiguration of FPGA[C] //Proc of the 4th IEEE ReConFig. Piscataway, NJ: IEEE, 2009: 386-391 [23]Xilinx Inc. System ACE configuration solution for Xilinx FPGAs,version3.0.1[EB/OL]. (2007-12-17)[2016-05-21]. http://china.xilinx.com/support/documentation/white_papers/wp151.pdf [24]Hemnath P, Prabhu V. Compression of fpga bitstreams using improved rle algorithm[C] //Proc of the 2nd IEEE Int Conf on Information Communication and Embedded Systems. Piscataway, NJ: IEEE, 2013: 834-839 [25]Xilinx Inc.Vivado design suite user guide embeded processor hardware design[EB/OL]. (2007-12-17)[2016-05-21]. http://china.xilinx.com/support/documentation/sw_manuals/xilinx2015_4/ug898-vivado-embedded-design.pdf [26]Xilinx Inc. Xilinx FPGA configuration details.[EB/OL].[2016-05-21]. http://www.eefocus.com/sxl630828191/blog/12-12/290582_7f03c.html (in Chinese) (Xilinx. Xilinx FPGA配置细节详解[EB/OL].[2016-05-21]. http://www.eefocus.com/sxl630828191/blog/12-12/290582_7f03c.html) [27]Department of Computer Science in University of Erlangen Nuremberg. Design methodology for embedded systems made upon small networks of hardware reconfigurable nodes and connections[EB/OL]. [2016-05-21]. http://www.reconets.de/bitstreamcompression/ [28]Seong S W, Mishra P. Bitmask-based code compression for embedded systems[J]. IEEE Trans on Computer-Aided Design of Integrated Circuits and Systems, 2008, 27(4): 673-685 [29]Koch D, Beckhoff C, Teich J. Bitstream decompression for high speed FPGA configuration from slow memories[C] //Proc of the 6th IEEE FPT. Piscataway, NJ: IEEE, 2008: 161-168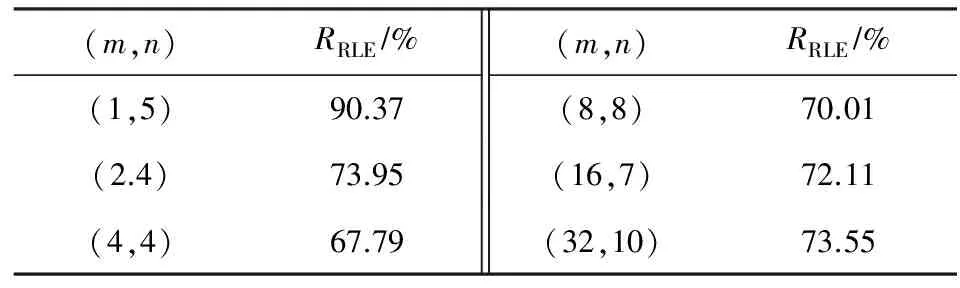
2.3 H-RLE压缩算法

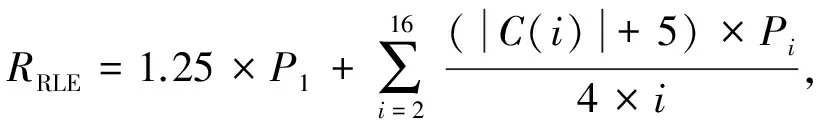



2.4 MH-RLE压缩算法


3 MH-RLE压缩算法性能测试与评价
3.1 实验数据
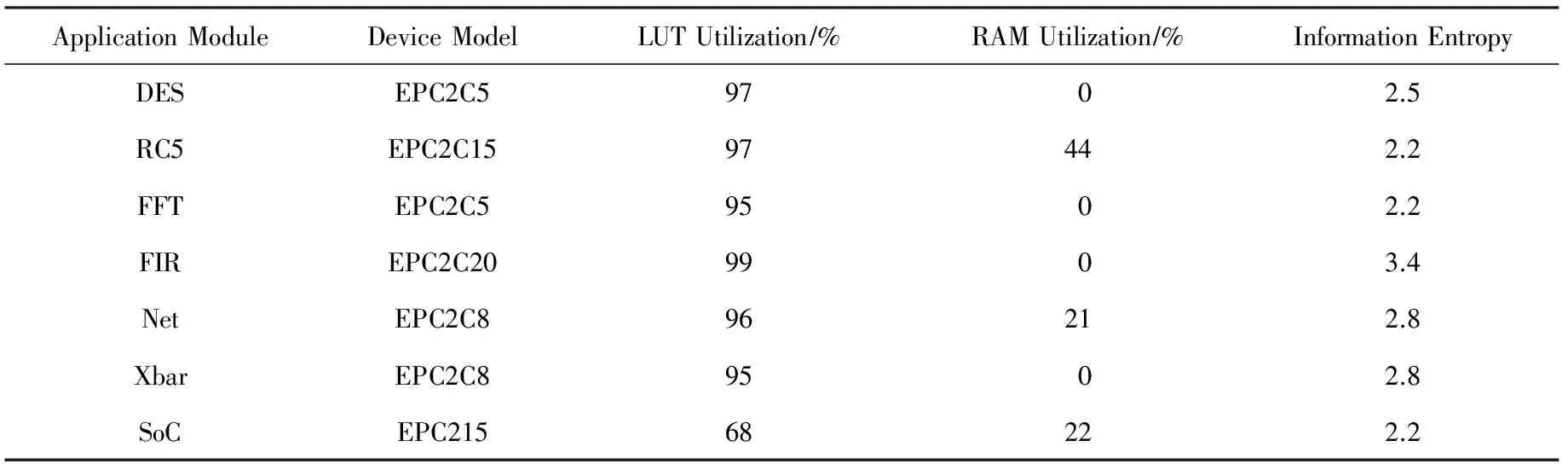


3.2 测试与评价

4 解压电路介绍


5 结论与展望

