基于网格热度值的船舶规律路径提取算法
李建江 陈 玮 李 明 张 凯 刘雅俊
1(北京科技大学计算机科学与技术系 北京 100083) 2(中国科学院电子学研究所 北京 100190) (willchen.ustb@gmail.com)
对移动目标历史轨迹数据的挖掘已成为目前研究的热点之一,其应用涉及到气象监测、交通流量控制、智能导航、犯罪行为检测等多个领域.然而,受特定背景、技术设备和人为等因素的影响,轨迹数据常常具有倾斜的分布,再加之先验知识不足,从而导致算法不稳定、可扩展性差.
移动目标不仅仅局限于人类自身,海运大数据给海事领域提供了可供挖掘的海量信息.利用这些信息分析船舶的运行规律不仅可以提高海运管理水平,还对航海安全有指导性的意义.船舶自动识别系统(automatic identification system, AIS)是一种数字辅助导航系统,它由相关硬件(包括船载设备、岸基设施等)和软件(涉及网络、现代通信、计算机、电子信息等技术)组成.随着无线通信、GPS(global positioning system)等相关技术的发展,海上AIS数据被用于规律路径提取,这对预测与理解移动目标活动的行为具有重要的意义.为此,本文借助网格方法对海量轨迹数据进行压缩,从而提出了基于密度度量方式“热度因子”的规律路径提取算法,为管理部门提供管理依据,有效地改善和提升管理者的决策水平.
1 相关工作
目前,挖掘移动目标轨迹已成为研究热点之一.GPS和移动设备的发展为用户行为习惯的挖掘提供了独特的机会[1].给定源和目的地可以分析个人频繁经过的轨迹并寻找个性化路线[2],根据位置驱动来分析人们的日常规律,从而发现热点地区[3].由于用户频繁经过的地方很可能是其感兴趣的空间,而分析用户频繁经过的地区又可以发现用户之间的相似度[4],这对于旅游推荐[5-6]等系统意义重大.人类轨迹的挖掘不仅对交通[7]、旅游、商业等有巨大帮助,还可用于检测一些异常行为[8].
目前,有很多方法可被用于分析移动目标的轨迹,比如基于图的聚类分析[9]、基于贝叶斯模型、Markov模型以及时间序列的轨迹分析[10],这些方法大都基于监督学习来推断人们的移动规律[11],需要设定目标移动的模式或形状[12],然后通过拟合外推出符合特定模式的轨迹[13].实际上,由于数据分布的不均匀以及沟通成本等现实问题,很难有足够的经验作为已知条件,并且现有的轨迹聚类方法很难将时间和空间位置信息进行有效结合,比如文献[14]给出了一种“划分-聚合”的TRACLUS轨迹聚类方法,该方法先将轨迹划分为一系列子轨迹,然后使用线段密度聚类方法再聚合成完整轨迹.但是,该方法没有考虑到轨迹数量的爆发式增长,可扩展性较差.文献[15]中使用网格方法来寻找城区中的热点区域,但需要给定初始阈值去筛选高密度网格,而且没有考虑到网格粒度的影响,所以其扩展性和适用性尚无法让人满意.由于移动目标的轨迹一般是由驾驶人的主观意愿和路网客观约束的结果,这种不确定性使得挖掘轨迹中的频繁模式显得尤为重要,而在这些频繁模式中规律路径又是海路交通中的一个重要特征[16-17].例如借助聚类和中心线拟合等路网提取方法从车辆的GPS轨迹中挖掘城市主干路网[18],在文献[19]中用一种投影的方法来提取这种长时间、可共享的路径,有效地避免了子路线指数般的生成.在路网交通轨迹分析中,不仅要考虑轨迹运动的几何信息,还要结合交通语义信息来确定道路交通类型,并根据变化类型进行增量信息融合[20].以上这些方法对于抗震救灾、导航定位等场合都非常重要.
船舶的航线分析和规划是现代海上交通管理系统必不可少的内容,Venskus等人[21]用一种自适应算法检测海洋交通中任何非标准的运动;Junghans等人[22]预测了目标运动区域内的轨迹以及该区域内的空间范围和方向,并利用线性回归方法确定区域内的目标运动模式;也有学者用贝叶斯模型[23]来构建一组关键路径作为支撑路径[24],能发现与该路径具有相似模式的所有路径.由于与基于密度的簇有着紧密关系,聚类算法可找出任意形状的簇,因此被广泛应用于目标轨迹的预测模型[25].
上述方法考虑了移动目标的某一特定模式的分析,但无法发现不同目标、不同形状的轨迹,而且可扩展性欠佳,无法适用于爆发式增长的海量轨迹数据.本文提出基于网格热度值的规律路径提取算法,该算法在压缩大量轨迹数据的同时又保持了轨迹的原有形状和密度信息,能有效地发现不同形状的规律路径.
2 数据准备和基本定义
先前关于路径挖掘的研究大多基于模式分类,此类方法的精确度完全依赖于其支撑路径的定义,效率不高且可扩展性较差.利用距离与密度,基于网格热度值的聚类算法可找出任意形状的轨迹簇,而且其效率也很高[26].图1给出了本文中目标规律路径提取的具体框架,可实现从给定目标的大量历史信息中提取出规律路径.

Fig. 1 The frame of rule path extraction based on the grids图1 基于网格的规律路径提取框架图
2.1 数据准备
移动目标的历史轨迹表示为空间上连续运动的位置点的集合,为了挖掘出海上移动目标的运动模式,本文采用AIS船舶数据来具体分析.不同于地面上移动目标的运动模式,船舶在水上的运动特征表现为灵活性差、速度较低、转向幅度较平缓、航行时空跨度大等特征,因此船舶的轨迹在空间位置上表现为光滑、时空跨度大的曲线集合.这里,定义R={P1,P2,…,Pi,Pi+1,…,Pnum}为在某个时间段内移动目标对应的轨迹点集合,其中,Pi=pi,ti表示移动目标对象在时刻ti经过的位置pi=(xi,yi).表1给出了部分AIS原始数据中目标的轨迹信息.
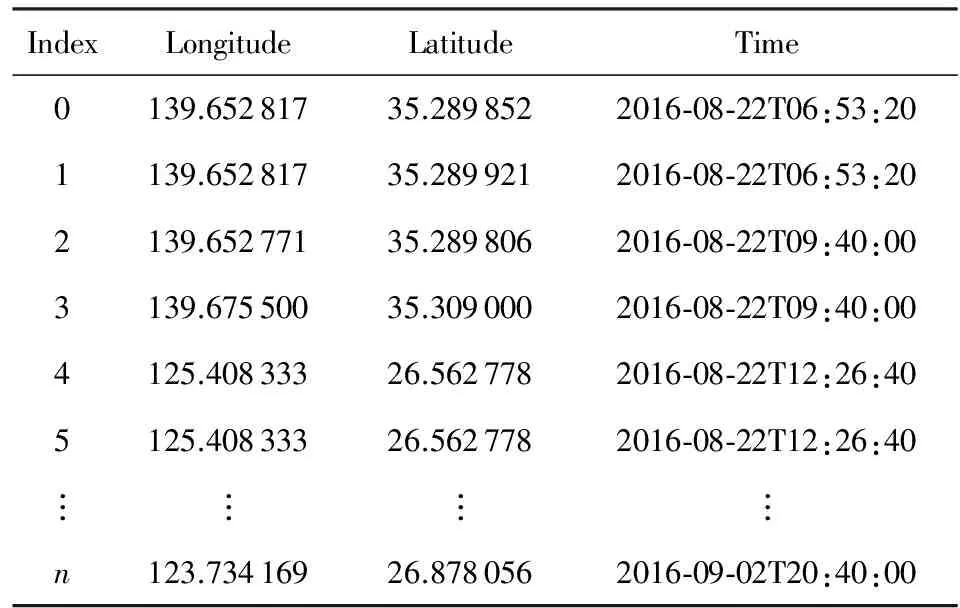
Table 1 The Data Points Set of AIS表1 AIS原始数据点集
2.2 网格映射
由于网格能将空间高维数据离散化,突破维数灾难[27],同时有效克服“距离”障碍,并且能配合有效的密度聚类算法隔离“噪声”.在本文中,网格粒度scale由网格划分层次l表示:
scale=360°×2-l,
(1)
式(1)表示将360°划分为2l份.其中,单位网格对应的角度用scale来表示,当前网格粒度的划分层次用l来表示.为了方便计算和理解,将经纬度映射到直角坐标系中,其转换公式为
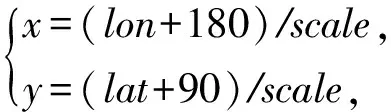
(2)
其中,x与y为第l层网格gxy的坐标,lon和lat分别为经纬度.为了尽可能在压缩数据量的同时又不丢失数据,本文给出了网格“热度值”的定义.其中,“热度值”指轨迹点落在一个网格的次数或频率,Vg表示为网格gxy的“热度值”,其计算方法为

(3)

Fig. 2 Original trace points and grid maps图2 原始轨迹点和网格映射图
其中,g=gxy表示当前网格;(x,y)′为轨迹点pi映射后的网格坐标;N为所有的轨迹点数;vi为一个二进制变量,其值等于1时表示点pi落到g内,其值等于0时表示没有落到该网格内.因此,利用式(1)与式(2),可以将给定的轨迹点映射至某个网格中.
如图2所示,左边的一系列轨迹点经过映射得到右边的网格点,其网格热度值V3,4=7,V3,3=2,V3,1=0,….因此,可记单个网格为Gi=gi,Vi,其中,gi表示网格的位置,Vi表示该网格的“热度值”,该“热度值”不仅蕴含了目标的“规律”信息,还在不丢失数据的前提下涵盖了密度信息,最重要的是能压缩大量的轨迹数据,提高效率.
2.3 方向定义
关于路径提取的研究,如基于网格的规律路径提取、基于图像边缘检测的路径提取[28]等研究,通过构造方向矩阵来判断路径的方向.方向矩阵通过对1个网格的所有邻居做标记来指示方向信息,该方法设计简单且易于实现,同时也带来了巨额的内存开销,而且对数据准确性依赖较高,抗干扰能力弱.因此,仅仅依靠邻居网格是无法正确判断路径方向的.此外,目标轨迹点与路径之间的关系还需要满足3个条件:
1) 一条路径上的轨迹点具有分布均匀、密度高、连续性好的特点;
2) 一组有序的轨迹点构成的路径应该是分段光滑、跨区域的,小短线不能作为路径;
3) 路径可以是开放的,也可以是闭合的,即路径的形状不一.
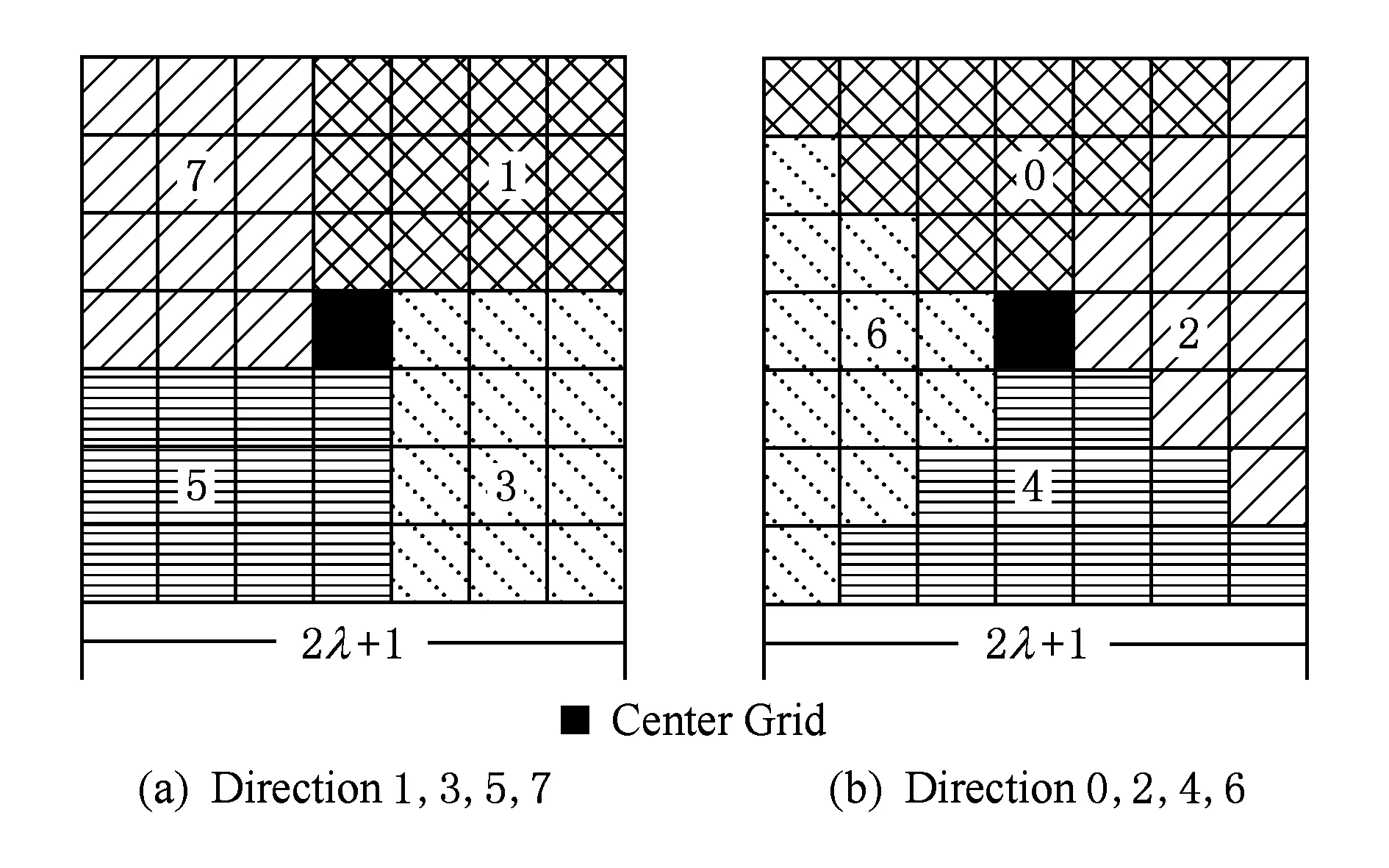
Fig. 3 Eight directions in the square图3 方形领域内8个方向示意图

根据轨迹点与路径之间的上述关系,针对的求解可得2个约束条件:

2) 在λ搜索到的一组光滑路径中,其全局平均误差不能超过δ2.

max(eg)≤δ1,g∈SN,
(4)
(5)

(6)
在本文中,λ的初始值可取初始网格划分层数l0,记为λ0.而l0的值可由原始轨迹点的经纬跨度来估算.定义第li层网格粒度下对应的滑动窗口步长为λi,且λi=k×λ0.则有:

(7)


(8)


(9)
由式(9)可知,其在第1象限内是单调递减函数,2△l与步长的增大倍数k之间存在最优解,而网格的层数l与轨迹精度密切相关.因此,给定1个网格划分l就可大致确定λ的取值,相应的误差也将得以估计;相反,给定误差值约束,则λ的范围也能大致估算出来.
2.4 相关性度量方式
空间自相关理论认为,空间位置邻近对象间的相关性要远远大于疏远的对象间的相关性,而且距离越近,相互关联的程度就越高.本文的路径提取算法使用基于局部热度因子来确定路径的方向,这里的热度因子不仅表示轨迹点的密度,还表示了其空间分布上的聚集程度.本文在由给定参数λ所确定的邻域中,不指定固定的密度和邻近阈值,而是结合密度、热度值和邻近关系来确定路径的方向信息.
局部热度因子表示为
(10)
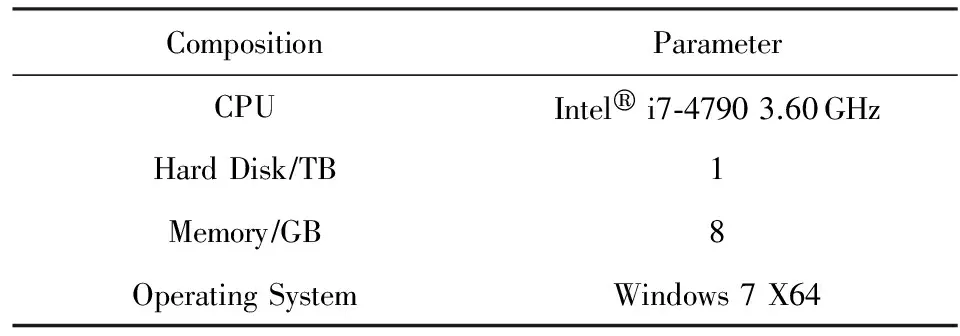
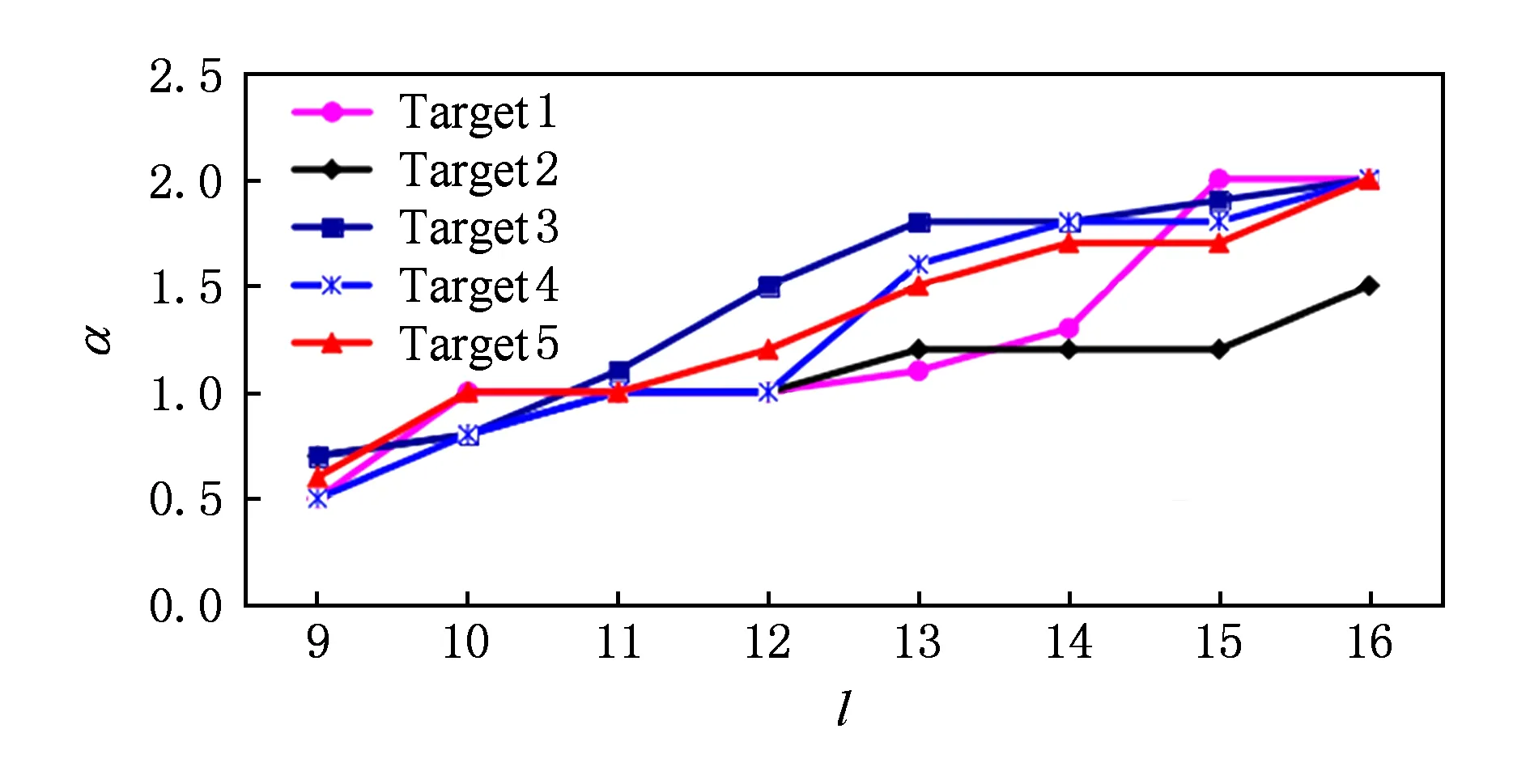
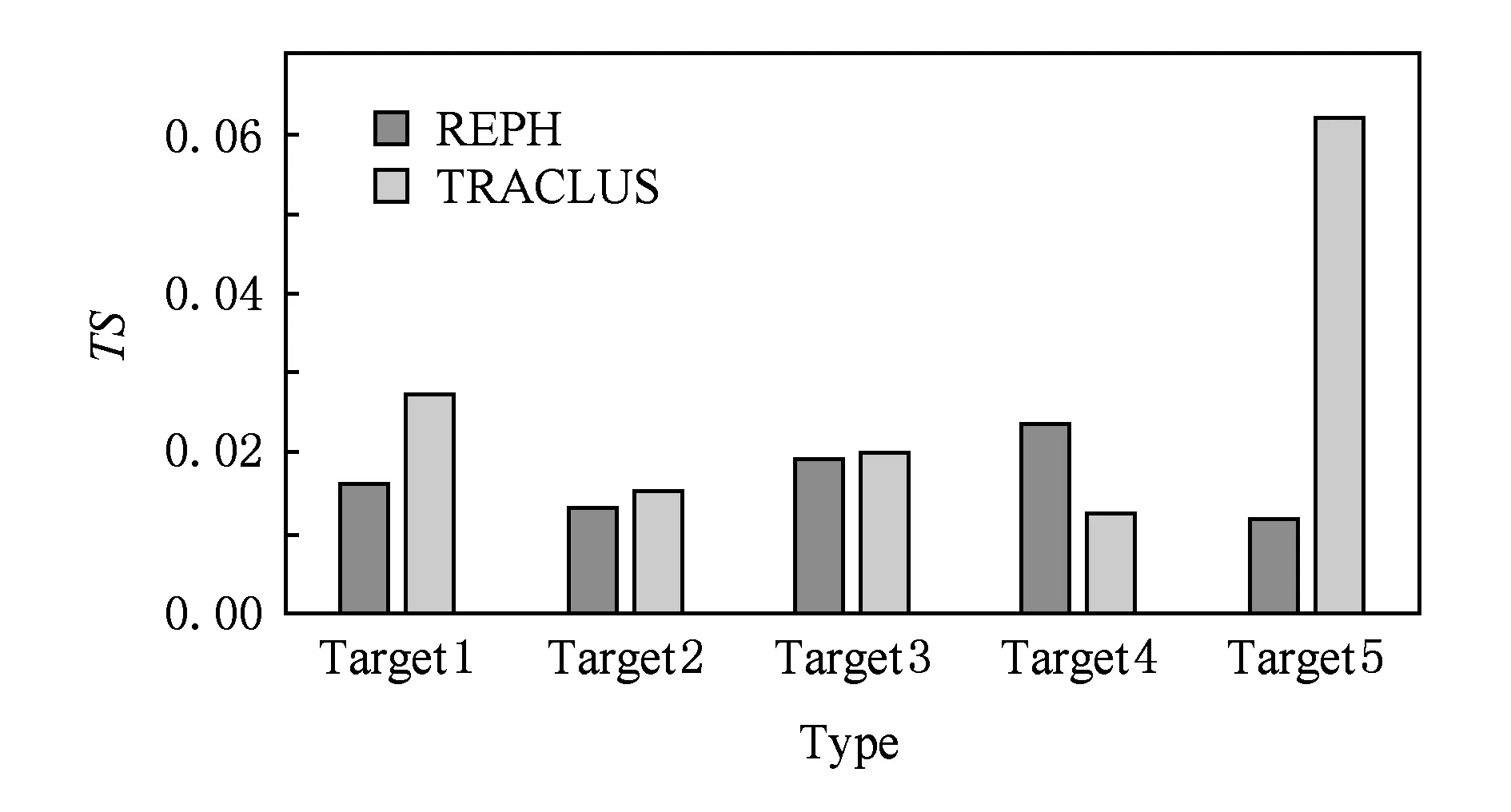
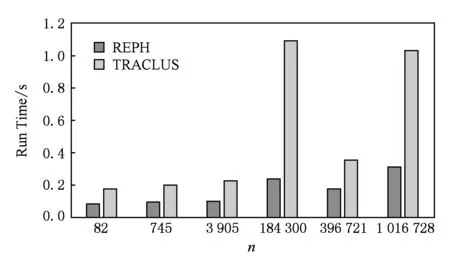
其中,rdk(g←g′)为第k个方向上网格g′到当前网格g的相对距离,该相对距离表示从g′到g所经过的最少网格数.为了更加精确地表示在某个方向上网格点的紧密程度,引入Tdk=2-q,0 (11) Fig. 4 The schematic of the heat factor 图4 热度因子影响解析示意图 判断完方向后,根据相对距离,按由小到大的顺序,将该方向的网格依次添加到对应路径栈中.当相对距离相等时,热度值大的优先入栈,直到该方向的所有网格都入栈.例如当前的路径轨迹点序列为Ri={3,1,2,1,1,1,1,2,4,5,4},则下一个窗口的中心点选为最后入栈的网格,如图5所示: Fig. 5 The schematic of the heat factor 图5 热度因子影响解析示意图 使用上述方法,依次向前滑动,直到该窗口内搜索不到任何点,则一条完整的路径搜索结束,如图6所示,当前路径序列为Ri={3,1,2,1,1,1,1,2,4,5,4,4,8,3,6,4,2,1,2,2,1}.很明显,上述搜索方法是一种在局部最优方向提取路径的贪婪算法.前面已讨论λ的求解能将局部最大误差和全局平均误差控制在某个范围内.所以,这种在局部最优方向提取路径的贪婪算法可在全局范围内得到不错的路径序列. Fig. 6 The schematic of the heat factor 图6 热度因子影响解析示意图 先从所有轨迹点中筛选出“起始点”,也就是一条路径的起始位置,这不仅能提高路径提取的准确性,也能减少路径提取的效率.首先,对“起始点”做3点定义: 1) 最边界点作为起始点的优先级最高; 2) 从“起始点”出发,只在单一方向上有路径,即在多个方向上有路径的点不作为起始点; 3) 热度区也可以作为“起始点”. 这里的“起始点”不仅指单个网格,而应该是一系列符合起始点定义的网格集合.为了简单起见,可从起始点集合中选取热度值最大的中心点作为“代表”.一条轨迹的起始点可被定义为S(g,c),其中,g为该起始点对应的网格集合的“中心点”,c表示起始点包含的网格数目.在一些分布规律性不强的轨迹点中,起始点的初始集合很可能为空,但这并不会影响路径提取的效果.在分布较为规律的轨迹中,对起始点的初始集合的筛选在很大程度上能够提高算法效率和精度. 算法1. 基于网格热度值的规律路径提取算法(RPEH). 输入:一组无序网格点集合R={g1,g2,…,gnum}、阈值λ; ① For eachgiinR ②Visit(gi)←False; ③ End For ④InitStack(s); ⑤ For eachgiinR ⑥ IfVisit(gi) is False then ⑦Push(s,gi); ⑧g←Pop(s); ⑨ADJs et=JudgeDirection(g); ⑩ IfADJs etis Null then 在算法1中,步骤①~④初始化原始网格和栈;在步骤⑤~⑦中依次取出一个点来判断其是否被访问过,如果没有被访问则将其入栈;步骤⑧⑨中,将栈顶元素取出,并计算λ确定的范围内的方向.JudgeDirection(g)是计算g周围8个方向的热度因子并比较其大小,然后选择热度因子影响最高的一个方向,并按照相对距离从小到大、热度值从大到小的顺序将该方向上所有网格存入ADJs et中;步骤⑩,当ADJs et=∅时,说明t周围的8个方向上已无可访问网格.此时,按从底到顶的顺序将栈s中的点依次输出,构成一条规律路径.接着返回到步骤⑤,以下一个网格为起点开始搜索;在步骤~中,当ADJs et≠∅时,依次将ADJs et的点入栈,并将每个点的访问状态标记为True,接下来跳转到步骤⑧继续进行递归搜索,一直到搜索不到为止;在步骤中,当所有的网格都被搜索过一遍后,该算法结束,并返回n条路径 大量实践发现,对于大部分移动对象来说,其运动路径都不会出现明显的棱角,在平直的道路上也不可能完全沿着直线运动;相反,往往受障碍物或其他对象的干扰而沿曲线运动.道格拉斯-普克曲线能使用较少的点保持曲线基本形状和趋势.该曲线给定阈值后可有效去除多余的点,并保留曲线的基本形态.一条移动目标的轨迹应该是分段光滑的. 本文通过设置局部的曲率阈值来去除路径上的异常点.除了路径的首末2个点,中间依次邻接的3个点形成一个夹角θ.当其值小于阈值α时,则删除3个点中位于中间的那个点.依次计算,直到删除该曲线所有的“尖角”点以形成一条较为光滑的曲线.如图7所示,该方法可有效去除路径中的“尖角”. Fig. 7 The process of exception handling图7 异常点处理示意图 插值在图像处理领域应用广泛,可有效消除轨迹中较为明显的“锯齿”现象. 三次样条是其中使用较为广泛的一种. 但是,当被插值点为稀疏分布时,该插值方法将带来比较大的误差.为了弥补该缺点,本文先使用贝塞尔曲线将插值点增多并保存轨迹原有的局部弯曲特性,然后利用样条插值方法对整体进行拟合,最终使路径提取的准确性得以提高.算法2给出了对RPEH算法提取出的路径进行异常点去除和光滑处理的过程. 算法2. 异常点去除和光滑处理算法(BAS). 输入:一条有序路径Ri={g1,g2,…,gm}、光滑度α; ① Fori←1 tom ② Doθ←Angle(gi-1,gi,gi+1) ③ Ifθ<αthen ④Remove(gi); ⑤i←i-1; ⑥ End If ⑦ End For 其中,步骤①~⑦去除搜索到的路径序列中的异常点;步骤⑧使用二阶贝塞尔曲线,对去除异常点后的路径序列中连续3点形成的夹角小于一定阈值的“尖角”来进行光滑处理;为实现对轨迹的整体拟合,步骤⑨使用了三次样条插值方法.其中,根据距离来估算三次样条的拟合采样点数,在该算法中设定至少需要20个采样点. 本节将主要从算法的准确性、可扩展性和性能这3个方面进行测试,并使用海上交通AIS数据[29]来验证该算法的有效性. 不同的聚类算法目标函数相差很大,有基于距离的,有基于图聚类和谱分析性质的,还有些是基于密度等.因此,还没有统一的标准进行聚类的评价,而应根据具体应用来具体分析.针对AIS数据的实际特点,本文使用2种方法对提出的基于网格热度值的规律路径聚类分析算法的聚类效果进行评价. 1) 外部方法.鉴于经纬度位置信息的优点,将每条路径通过可视化的方法展示出来以便进行评价.该评价方法具有简便、直观的特点. 2) 内部方法.路径的聚类效果可根据轨迹的内部信息来评价.为具体评价聚类效果,本文使用如下3种度量方式: 为所有点的平均分离度.该值越大,则轨迹簇间的分离效果越好;反之,则越差.定义TS=TRSR为评价轨迹簇聚类效果的指标,该值越接近0说明效果越好,而当值大于等于1时说明聚类效果较差. ③ 异常点分离度.当轨迹簇数为1时,SR不再适用.为了更好地评价1条轨迹的聚类效果,可用该轨迹上的异常点分离度SP来替代SR. 表2给出了测试所用运行环境的相关配置情况,表3给出了测试的AIS数据集的类型和大小.AIS数据不仅包括如船号、类型这样的静态数据,还包括类似经纬度和时间这样的动态数据.此外AIS数据还具有精度高、丢失数据少的特点.因此,根据船舶的具体情况和测量经验,网格层数l取值范围为 [9,16]. Table 2 The Configuration of the Running Environment表2 测试所用运行环境的配置情况 Table 3 Test Data Set表3 测试数据集 Fig. 8 The diagram of the relationship between l and α图8 网格划分层数l与异常点去除阈值α关系图 针对上述5种典型目标,实际测得的网格层数l与阈值α折线图如图8所示.从图8可以看出,在网格划分粒度不同的情况下,这5种类型目标的变化不是很剧烈,即说明α的值对轨迹的精度影响并不大,且网格层数在9 ~ 16之间时,α取值范围在[0.5,2].可取α初始值为1,然后迭代寻找其最优值.图9给出α=1时,层数l与λ的关系柱状图.从图9可以看出,每当层数l增加1,λ会增大2倍左右.综上所述,当选取某个初始网格划分粒度,例如l0=11之后,则取λ0=11,α0=1.要提取某个目标轨迹的路径,可通过轮换变量法依次求解l,λ,α这3个变量的最优值. Fig. 9 The diagram of the relationship between l and λ图9 网格划分层数l与λ关系图 本文选取5种不同类型船舶,根据提出的基于网格热度值的规律路径聚类分析算法,计算出其轨迹,并与实际的目标轨迹进行比较,结果如图10所示.从图10可以清晰地看出,这5种类型船舶的航行路线基本符合它们的活动路线. Fig. 10 The visual figure of target track图10 目标轨迹航线可视化图 表4给出了5个目标轨迹簇的紧凑度和分离度的统计结果.可以看出,Target4的TS值最大,说明其聚类效果最差,这符合Target4的实际轨迹最为复杂这一真实情况,但其他几个目标的聚类效果较好.对于目标轨迹复杂的情况,我们会在后面的研究中做进一步的介绍. Table 4 The Evaluation Results of Cluster表4 聚类评价结果 图11给出了本文提出并实现的REPH算法与常用的TRACLUS[14]算法之间聚类效果的对比情况.可以看出,除了Target4之外,REPH算法比TRACLUS算法的TS都要小,说明当目标轨迹比较规律时,本文提出并实现的REPH算法其聚类效果明显更好. Fig. 11 The comparison of clustering effect with RPEH and TRACLUS图11 与TRACLUS算法的聚类效果对比图 本文提出并实现的基于网格热度值的船舶规律路径提取算法,其进行聚类分析所耗费的时间如图12所示.从图12可以看出,随着原始轨迹点数目的爆发式增长,该算法所花费的时间并未急剧增加,而是以较为平缓的趋势(图12中的虚线)增长,其原因在于本文提出的方法在很大程度上压缩了数据,提高了计算效率. Fig. 12 The relationship of trace points and running time图12 轨迹点数和运行时间关系图 从图12还可以看出,原始轨迹点数为184 300,396 721,1 016 728的目标轨迹压缩接近100%,这些目标虽有十几万甚至上百万个轨迹点,但基本上都集中在一个固定区域,这也揭示了在图12中原始轨迹点数为184 300的目标的计算时间反而比原始轨迹点数为3 905的目标轨迹的计算时间短的原因.总的来说,通过数据压缩,本文提出的算法的性能显著提高,能够满足实际需要. 图13给出了本文提出并实现的REPH算法与常用的TRACLUS算法之间性能的比较,从中可以看出本文提出并实现的REPH算法的性能明显优于TRACLUS算法,尤其是当数据量较大的时候.因此,无论是从聚类效果还是从性能方面,本文提出并实现的基于网格热度值的规律路径提取算法REPH都有明显的优势. Fig. 13 The comparison of clustering effect with RPEH and TRACLUS图13 与TRACLUS算法的聚类性能对比图 本文提出了一种基于网格热度值的船舶规律路径提取算法,通过计算局部方形邻域内的热度因子来判断路径的方向,并利用异常点去除和光滑处理相结合的方法,能够有效地发现移动目标不同形状的轨迹.最后,以可视化的方式对提取出的路径进行了直观展示,并通过算法精度和性能测试表明了算法的可行性.实验结果表明:与常用的TRACLUS算法相比,本文提出并实现的基于网格热度值的船舶规律路径提取算法具有更好的聚类效果而且性能更高. 本文提出的算法属于无监督的聚类分析算法,当遇到分布稀疏且不规律的轨迹时其局部误差可能会变大.因此,在后续的工作中,将进一步引入时间密度和时间序列来对复杂的轨迹进行处理.此外,我们还会引入基于活动图的复杂模型来表示目标的运动模式,这种模型不仅能识别规律的航线,还能处理复杂的船舶活动状态和时序等信息.本文的规律路径提取算法无论是对未来研究工作的进一步开展还是对海上船舶的行为预测都有重要意义,对海陆交通提供更有效的服务奠定了基础. [1]Choujaa D, Dulay N. Predicting human behaviour from selected mobile phone data points[C] //Proc of the 12th ACM Int Conf on Ubiquitous Computing. New York: ACM, 2010: 105-108 [2]Chang Kaiping, Wei Lingyin, Yeh M Y, et al. Discovering personalized routes from trajectories[C] //Proc of the 3rd ACM SIGSPATIAL Int Workshop on Location-Based Social Networks. New York: ACM, 2011: 33-40 [3]Farrahi K, Gatica-Perez D. What did you do today?Discovering daily routines from large-scale mobile data[C] //Proc of the 16th ACM Int Conf on Multimedia. New York: ACM, 2008: 849-852 [4]Li Quannan, Zheng Yu, Xie Xing, et al. Mining user similarity based on location history[C] //Proc of the 16th ACM SIGSPATIAL Int Conf on Advances in Geographic Information Systems. New York: ACM, 2008: Article No.34 [5]Zheng Yu, Zhang Lizhu, Xie Xing, et al. Mining interesting locations and travel sequences from GPS trajectories[C] //Proc of the 18th Int Conf on Worlid Wide Web. New York: ACM, 2009: 791-800 [6]Alivand M, Hochmair H. Extracting scenic routes from VGI data sources[C] //Proc of the 2nd ACM SIGSPATIAL Int Workshop on Crowdsourced and Volunteered Geographic Information. New York: ACM, 2013: 23-30 [7]Zheng Jiangchuan, Lionel M. An unsupervised framework for sensing individual and cluster behavior patterns from human mobile data[C] //Proc of the 2012 ACM Conf on Ubiquitous Computing. New York: ACM, 2012: 153-162 [8]Liao Lin, Patterson D J, Fox D, et al. Learning and inferring transportation routines[J]. Artificial Intelligence, 2007, 171(5/6): 311-331 [10]Huang Xin, Luo Jun, Wang Xin. Finding frequent sub-trajectories with time constraints[C] //Proc of the 2nd ACM SIGKDD Int Workshop on Urban Computing. New York: ACM, 2013: Article No.13 [11]Zheng Yu, Li Quannan, Chen Yukun, et al. Understanding mobility based on GPS data[C] //Proc of the 10th Int Conf on Ubiquitous Computing. New York: ACM, 2008: 312-321 [12]Zhang Kun, Wang Cuirong, Li Shaoheng. An automatic detection and segmentation algorithm of video multiple moving targets for computer vision[C] //Proc of the 7th Int Conf on Internet Multimedia Computing and Service. New York: ACM, 2015: Article No.48 [13]Griffin T, Huang Y, Seals S. Routing-based map matching for extracting routes from GPS trajectories[C] //Proc of the 2nd Int Conf on Computing for Geospatial Research & Applications. New York: ACM, 2011: Article No.24 [14]Lee J G, Han Jiawei, Whang K Y. Trajectory clustering: A partition-and-group framework[C] //Proc of the 2007 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2007: 593-604 [15]Hio C, Bermingham L, Cai Guochen, et al. A hybrid grid-based method for mining arbitrary regions-of-interest from trajectories[C] //Proc of Workshop on Machine Learning for Sensory Data Analysis. New York: ACM, 2013: 5-8 [16]Guo Limin,Ding Zhiming,Hu Zelin,et al. Prediction of uncertainty trajectory based on road network[J]. Journal of Computer Research and Development, 2010, 47(1): 104-112 (in Chinese) (郭黎敏, 丁治明, 胡泽林, 等. 基于路网的不确定性轨迹预测[J]. 计算机研究与发展, 2010, 47(1): 104-112) [17]He Yuanhao, Wei Haiping, Zhou Ye, et al. Algorithm for extracting regions of interest from vehicle GPS trajectory[J]. Engineering of Surveying & Mapping, 2016, 25(5): 47-51 [18]Ouyang Hong, Liu Jianxiong, Liu Yizhi, et al. An extraction method of road network based on walking GPS trajectories[J]. Computer & Modernization, 2014(2): 124-128 [19]Falvi G, Pedersen T B. Mining long, sharable patterns in trajectories of moving objects[J]. Geoinformatica, 2009, 13(1): 27-55 [20]Yang Wei,Ai Tinghua. A method for road network updating based on vehicle trajectory big data[J]. Journal of Computer Research and Development, 2016, 53(12): 2681-2693 (in Chinese) (杨伟, 艾廷华. 基于车辆轨迹大数据的道路网更新方法研究[J]. 计算机研究与发展, 2016, 52(12): 2681-2693) [21]Venskus J, Kurmis M, Andziulis A, et al. Self-learning adaptive algorithm for maritime traffic abnormal movement detection based on virtual pheromone method[C] //Proc of Int Symp on Performance Evaluation of Computer and Telecommunication Systems. Piscataway, NJ: IEEE, 2015: 1-6 [22]Junghans C, Gertz M. Modeling and prediction of moving region trajectories[C] //Proc of ACM SIGSPATIAL Int Workshop on GeoStreaming. New York: ACM, 2010: 23-30 [23]Shiga M, Mamitsuka H. Variational Bayes co-clustering with auxiliary information[C] //Proc of the 4th MultiClust Workshop on Multiple Clusterings, Multi-View Data, and Multi-Source Knowledge-Driven Clustering. New York: ACM, 2013: Article No.5 [24]Deshmukh A A, Aylett R. Exploring socially intelligent recharge behaviour for human-robot interaction[C] //Proc of the 2014 ACM/IEEE Int Conf on Human-Robot Interaction. New York: ACM, 2014: 150-151 [25]Park N H, Lee W S. Statistical grid-based clustering over data streams[J]. ACM SIGMOD Record, 2004, 33(1): 32-37 [26]Hung C C, Peng W C, Lee W C. Clustering and aggregating clues of trajectories for mining trajectory patterns and routes[J]. The VLDB Journal, 2015, 24(2): 169-192 [27]Hinneburg A, Keim D A. Optimal grid-clustering: Towards breaking the curse of dimensionality in high-dimensional clustering[C] //Proc of the 25th Int Conf on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1999: 506-507 [28]Neves R F P, Zanchettin C, Mello C A B. An adaptive thresholding algorithm based on edge detection and morphological operations for document images[C] //Proc of ACM Symp on Document Engineering. New York: ACM, 2013: 107-110 [29]Cai Xinmei. AIS application and development[J]. Mechanical and Electrical Equipment, 2011, 28(2): 28-30 (in Chinese) (蔡新梅. AIS应用与发展[J]. 机电设备, 2011, 28(2): 28-30)



3 规律路径提取算法
3.1 起始点筛选
3.2 规律路径提取算法
3.3 异常点去除



4 实验与结果
4.1 评价指标
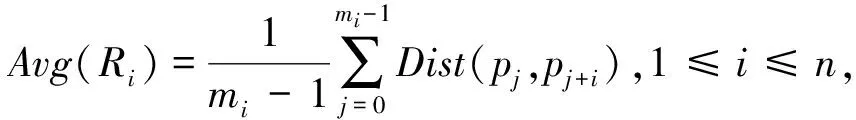
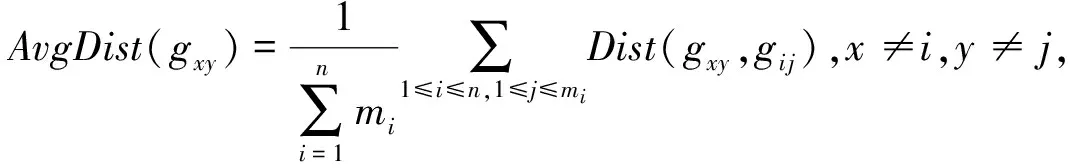
4.2 数据集


4.3 聚类效果评价


4.4 性能对比

5 总 结