基于主成分特征的快速分形图像压缩算法

张爱华，唐婷婷，汪玮玮，张 璟

(南京邮电大学 理学院，江苏 南京 210023)

0 引 言

在如今以计算机技术为基础的信息化社会[1]，图像资源丰富了人们的生活，图像通信的需求日益增长，所以对准确、高效的图像压缩方法的需求也更为迫切。分形是对没有特征长度但具有一定意义下的自相似图像和结构的总称。随着多媒体信息的发展，生活中对于图像压缩的需求日益增加。传统编码研究已经比较成熟，但图像质量和编码效率难以提高。因此许多新的图像压缩编码相继提出，基于分形的图像压缩编码就是其中一种。它利用图像的自相似性及比例特性[2]进行图像压缩，通过减少图像几何冗余来实现压缩。把像素点灰度值的顺序排列看成向量是图像压缩编码中常见的做法，在分形压缩编码中，传统特征向量法具有维数高[3]的缺点，高维时邻近搜索效果也不好，导致编码耗时过长。

主成分分析法[4]是统计学的一种重要方法，用于数据集简化，可由线性变换将原始数据变换为一组各维度线性无关的表示，用于提取数据的主要特征分量，适用于对各种高维数据进行降维。主成分分析法近年来在图像识别、去噪、重构方面都有应用，在图像压缩上主成分分析法可以排除众多信息互相重叠造成的冗余[5]。因此文中基于基本分形图像压缩理论，用主成分分析法构造图像特征，减少了搜索时间，为解决分形图像编码耗时过长的缺点提供了有效的方法。

1 基本分形算法

在基本分形算法[6-7]，把待编码的图像I分割成一组互不重叠的大小为n×n的R块以及尺寸为2n×2n的D块(D块允许有重叠)。求像素平均，将D块收缩为R块大小与R块匹配，所有收缩过的D块经过8个等距变换后构成码本Ω。为了寻求R块的最佳匹配块，需要解决下面的极小化问题：

‖R-(s·Dm+o·I)‖=

(1)

其中，m为R块的最佳匹配块序号；s为对比度因子；o为亮度偏移。

通常解决问题1是十分困难的，在实际应用中，通常忽略式1中的约束|s|<1，对不满足约束的对比因子作截断处理以补偿[8]。因此，式1的内层约束极小化问题转化为下述问题进行求解：

(2)

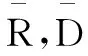
此时，匹配误差为：

(3)

接着用全搜索法求解问题1的外层极小化问题：

(4)

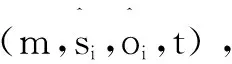
文中先对图像子块做标准化处理[10-11]，然后做主成分分析处理，也就是先求出其协方差，通过求协方差的特征值和特征向量，找到最大特征值对应的向量，作为原图像子块的主成分，通过求主成分对应向量来定义图像规范块的特征。在搜索匹配块时，在初始匹配块的邻域内搜索主成分特征接近的匹配块，搜索大小由预先设置的剔除条件确定。

2 算法理论依据

2.1 主成分特征的理论基础

在基本分形做法中，图像块被读取的形式往往是矩阵。而在矩阵理论中，特征值代表了信息量。特征值和特征向量求法众多，图像子块特征[12]往往与搜索的准确性以及解码图像质量息息相关，因而选好图像块的特征是关键。主成分分析过程能够去除图像的相关性[13]，能够对图像信息进行有效降维。文中采用如下方式来定义图像块的特征：

定义1：设大小为n×n的图像块X=(xi,j)∈RN×N，对数据X做标准化处理，即对每一个指标分量做标准化处理：

(5)

其中样本均值和样本标准差为：

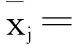
(6)

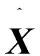
(7)

也就是主成分分析法求解了如下的特征问题：

λiui=Cui,i=1,2,…,n

(8)

其中，λi为C的一个特征值；ui为相应的特征向量。

对特征向量按特征值大小降序排列，仅需要k个主成分时，主成分分析法的变换表示为：

(9)

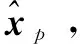
定义2(最大主成分特征)：一个图像子块X=(xi,j)n×n的主成分特征可以定义为：

(10)

理论基础为下述定理并给出证明：

定理：设R,D∈RN×N，则有不等式:

(11)

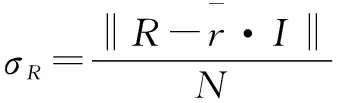
证明：定义子块B=[bi,j]n×n∈RN×N为：

可以得到‖B‖2=2N。

由柯西—许瓦兹[16]不等式知：|〈x,y〉|2≤〈x,x〉〈y,y〉或|〈x,y〉|≤‖x‖·‖y‖。

|S(R)-S(D)|2=

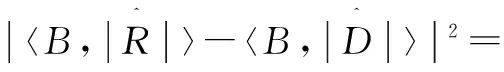
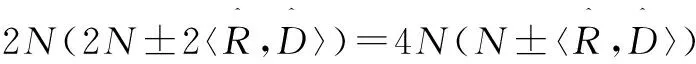
(12)

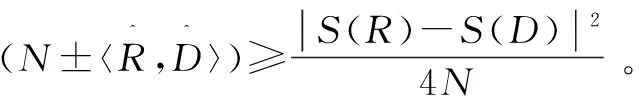
由式4和式12可知：

E(R,D)2=

(13)

2.2 搜索方案

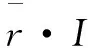
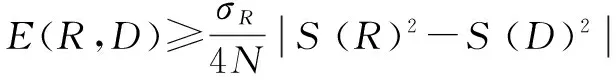
上式表明：若D块和R块的主成分特征相差较大，则匹配误差也较大，此时D不能匹配R；反之，如果D匹配R，即E(R,D)最小，由式11可知S(D)应该与S(R)非常接近。它表明R块的最佳匹配D块在主成分特征意义下一定是与R最相近的Dc∈Ω(Dc称为初始匹配块)的近邻。搜索时，先将码本中的D块求取其主成分特征，再按升序进行排列[18]，即满足S(Di)≤S(DI+1)。再使用二分法在主成分特征中搜索与S(R)相差最小的初始匹配块:

Dc={D∈Ω|min|S(D)-S(R)||}

(14)

最后，在邻域N(Dc)={DI∈Ω:l≤|i-c|≤r}中搜索最佳匹配块Dm(i)，使匹配误差E(R,Dm(i))<ε(ε为误差阈值)。显然N(Dc)∈Ω，将搜索空间变为局域搜索。编码时间会因搜索空间缩小而减少，从而达到加快编码速度的效果。

此外，研究表明，码本Ω中的小方差码本块可以预先排除[19]，不仅能减少码本容量，而且可以提高解码图像的质量。因此，可用缩减后的容许码本Ωη={D∈Ω:σD≥η}去置换码本Ω。

2.3 仿真算法描述

(1)把图像分成互不重叠的B×B块，记为R块，其中每个像素点的灰度值做标准化处理R∈N。以纵横方向步长均为δ的像素生成尺寸为2B×2B的D块，再对每个图像块采用4-邻域像素平均得到B×B大小的块，考虑8种等距变换，组成子块集合构成码本Ω。

(2)设定初始化参数τ>0，码本块的标准阈值为η，误差阈值设为ε，初始邻域半径为k，扩域步长为L。

(3)设定码本阈值η>0，把缩减后的容许码本记为Ωη：Ωη={D∈Ω|σD≥η}。

(4)计算每个D∈Ωη的主成分特征S(D)，并按照S(D)进行升序排列。

(5)计算R的标准差。如果σR≥τ，则计算R块的主成分特征S(R)，用二分搜索法在码本Ωη中找到与R特征接近的初始匹配DC块，搜索过程在DC的左右方向进行，直到满足E(R,Dm(i))<ε(ε为误差阈值)为止。

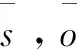
(7)对其他的R块(σR≥τ)，重复步骤5、6。

3 仿真实验及结果

图像仿真采用方块分割,实验对象为三幅不同类型512×512标准测试图像，它们分别是Lena,Boats,Peppers。选取R块大小为8×8，D块大小为16×16，步长σ=8，仿真程序使用MATLAB 2009编写，测试参数为编码时间(s)，峰值信噪比PSNR(dB)[20]。

通过实验将文中算法与基本算法的编码性能进行比较。主成分特征算法的编码时间与解码图像质量跟R块的分类阈值τ，容许码本阈值参数η，搜索效果与邻域半径大小k有关。对于参数τ和η，固定其取值，默认τ=4，η=30。根据三幅图像的仿真数据，将文中算法同基本算法的结果列表进行比较分析。

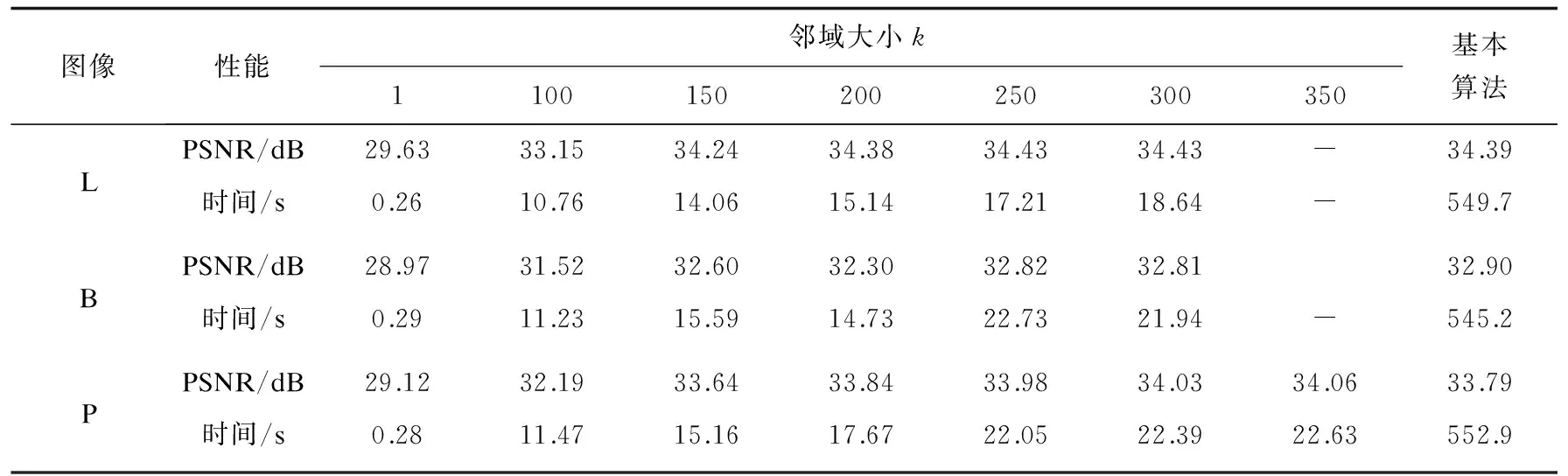
表1 文中算法随邻域k变化的实验结果

下面针对选用的三幅图像，在相同实验条件下，测试基本分形编码方法与文中方法(τ=4，η=30)的编码性能优劣，实验结果见表1。从表中数据可以看出，在k=100重构图像质量平均下降1.41 dB的情况下，可以加快平均编码速度48倍以上。文中给出在k=100时，三幅测试图的基本分形算法结果和文中分形算法结果，见图1。

图1 算法结果

从表1和图1可知，主成分特征算法与基本分形算法相比，从主观上看，基于主成分特征算法基本上不改变重构图像的质量；从客观上看，基本算法、文中算法可以在不影响高信噪比的基础上，减少运算时间，提高结构相似度。综上所述，文中算法可以在保证一定图像质量的前提下，大幅提高编码速度和结构相似度。

4 结束语

传统分形压缩编码中通常具有提取的图像特征冗余过多的缺点，文中提出了一种基于主成分分析法的分形压缩改进方法，通过对图像子块尽可能提取有效信息，然后用该信息定义图像特征，在不影响图像质量的前提下，提高了编码速度。全局搜索通常耗时较长，文中引进邻域搜索，可以根据搜索情况来调节搜索范围，有较强的灵活性。实验结果表明，该算法相对基本分形算法更加简洁有效。

参考文献：

[1] 冯泽森,王崇国.计算机与信息技术基础[M].第3版.北京:电子工业出版社,2007.

[2] FALCONER K.分形几何:数学基础及其应用[M].第2版.北京:人民邮电出版社,2007.

[3] 李高平.分形法图像压缩编码[M].成都:西南交通大学出版社,2010.

[4] 刘 涛,杨风暴.主成分分析在图像压缩中的应用[J].哈尔滨师范大学自然科学学报,2008,24(4):69-72.

[5] 鲁书山,沈小林,樊凯强.主成分分析法在数字图像压缩中的的应用[J].科技与创新,2016(23):98.

[6] JACQUIN A E.Image coding based on a fractal theory of iterated contractive image transformations[J].IEEE Transactions on Image Processing,1992,1(1):18-30.

[7] HE Chuanjiang,XU Xiaozeng,YANG Jing.Fast fractal im-

age encoding using one-norm of normalised block[J].Chaos Solitons & Fractals,2006,27(5):1178-1186.

[8] 杨兴全.基于分形理论的图像压缩研究[D].哈尔滨:黑龙江大学,2008.

[9] BARNSLEY M F,SLOAN A D,ELTON J H,et al.Fractal transform compression board:US,US5384867A[P].1995.

[10] 张 敏,李陶深,钟淑瑛.基于Matlab的主成分分析方法(PCA)的实现[J].广西大学学报:自然科学版,2005,30:74-77.

[11] 赵慧琳,王林泉,葛 元.人脸图像定位与标准化算法[J].计算机工程,2003,29(22):158-160.

[12] 袁宗文,鲁业频,杨汉生.半叉迹特征的快速分形图像编码[J].计算机工程与应用,2016,52(3):197-201.

[13] 姜 虹.主成分分析的图像压缩与重构[J].电子设计工程,2012,20(5):126-128.

[14] 李俊秀.基于主成分分析的半局部块匹配图像降噪算法研究[D].太原:中北大学,2014.

[15] ZHANG Lin,ZHANG Lei,MOU Xuanqin.FSIM:a feature similarity index of image quality assessment[J].IEEE Transactions on Image Processing,2011,20(8):2378-2386.

[16] 周一鸣,张 超,张曾科.基于图像子块特征的快速分形图像编码算法[J].计算机应用研究,2008,25(2):458-459.

[17] 何传江,黄席樾.基于图像块叉迹的快速分形图像编码算法[J].计算机学报,2005,28(10):1753-1758.

[18] HE C,YANG S X,HUANG X.Variance-based accelerating scheme for fractal image encoding[J].Electronics Letters,2004,40(2):115-116.

[19] 庄振静,何传江,申小娜.基于规范块半范数的快速分形编码算法[J].计算机工程与应用,2010,46(2):170-173.

[20] 汪明华,李高平.基于相似比的变邻域搜索的快速分形编码算法[J].西南民族大学学报:自然科学版,2016,42(6):682-687.