基于权重自适应形态学的周期性噪声去除方法

戴 丹，张兴刚

(1.贵州大学 计算机科学与技术学院，贵州 贵阳 550025； 2.贵州大学 物理学院，贵州 贵阳 550025)

0 引 言

数字图像的噪声主要产生于图像的获取和传输过程。图像去噪是指减少或去除数字图像中的噪声的过程。去噪效果的好坏直接影响到图像分割、图像识别等后续的图像处理效果。根据实际图像特点及噪声特点，国内外研究人员提出了多种去噪算法[1-4]。周期性噪声一般产生于图像采集过程中的电气或电机的干扰，表现为图像中周期性的冲击[5]。周期性噪声不但会影响图像的质量，还会破坏图像所携带的信息，因此需要去除。去除周期性噪声的传统方法是在频域进行处理，但是，在滤除周期性噪声的同时容易造成图像的失真或降噪效果不理想[6]。Yaroslavsky等提出利用维纳滤波去除周期性噪声[7]，该方法需要建立精确的噪声模型，会耗费大量的时间而且比较困难。Aizenberg等提出了频率中值滤波器[8]和窗口高斯陷波滤波器[9]以去除周期性噪声。频率中值滤波器在选择阈值和除子时需要多次实验；窗口高斯陷波滤波器需要人工选择阈值。Ji等提出了软形态学滤波器[10]，设定两个满足条件的结构元素和膨胀腐蚀的次数，然后利用膨胀腐蚀的方法去除周期性噪声。该方法比较简单，但去噪效果不是很理想。

根据周期性噪声的特点，文中给出了一种基于权重自适应形态学的周期性噪声去除方法。根据噪声特点，采用不同尺度和方向的结构元素来构建权重自适应的复合级联滤波器，并对其进行了仿真实验。

1 基本形态学滤波

数学形态学是分析几何形状和结构的数学方法，基于集合理论与晶格理论，它的目标是定量描述出图像的几何结构。形态学的基本思想是利用一个结构元素去探测一个图像，目的是寻找原始集合的特征，并进行图像处理，得到结果与结构元素的一些特性有关[11]。

形态变换按照应用场景可以分为两种形式：二值变换和灰度变换。二值变换处理集合，灰度变换处理函数。文中探讨灰度图像的形态学变换。形态学基本变换包括腐蚀、膨胀、开运算和闭运算。这四种基本变换的定义如下[12]：

设f(x,y)是输入的灰度图像，b(x,y)是结构元素，f(x,y)关于b(x,y)的形态学膨胀和腐蚀的公式分别为：

(f⊕b)(s,t)=max{f(s-x,t-y)+b(x,y)|(s-x),(t-y)∈Df;

(x,y)∈Db}

(1)

(f⊖b)(s,t)=min{f(s+x,t+y)-b(x,y)|(s+x),(t+y)∈Df;

(x,y)∈Db}

(2)

f(x,y)关于b(x,y)的开运算和闭运算分别为：

(f∘b)=(f⊖b)⊕b

(3)

(f·b)=(f⊕b)⊖b

(4)

灰度开运算一般能平滑图像的轮廓，消减狭窄的部分，抹平突出的细节；灰度闭运算也能平滑图像的轮廓，但它主要是填充背景中狭窄以及凹陷的部分，消除小洞[13]。根据灰度开、闭运算的这些作用，可以设计去除图像中噪声的形态学滤波器。通过对开运算和闭运算的组合运用，可构成形态学开-闭滤波器(OCF)和形态学闭-开滤波器(COF)。其定义分别如下：

OCF(f)=(f∘b)·b

(5)

COF(f)=(f·b)∘b

(6)

根据集合运算与形态运算的特点，OCF和COF具有递增性、平移不变性、幂等性和对偶性等性质[14]。

2 权重自适应的多方向形态学滤波

在使用形态学对图像进行去噪的过程中，适当地选择结构元素的大小和形状可以提高去噪的效果。而且，若使用不同尺度和方向的多结构元素，可以更多地保持图像的几何特征。因此在提出的形态学去噪算法中将使用不同尺度的结构元素对图像的周期性噪声进行串行处理，并将不同方向的串行处理结果与原始图像进行差异值计算以自动确定权值向量。

2.1 多方向元素选取

虽然形态学开-闭滤波器和形态学闭-开滤波器可以同时抑制图像中的正负脉冲噪声,但若只使用单一结构的结构元素，则输出图像中与结构元素的大小和方向不同的几何特征不易被保留。所以文中不采用单一结构元素，而是采用不同尺度和方向的结构元素序列构成复合形态滤波器。由于方形和圆形的结构元素会使图像的边缘产生较大的损失，而且结构元素越大，输出越模糊不清[15]，因此，采用不同方向的线性结构元素，结构元素的大小限制在3×3到5×5的范围内。将结构元素表示为集合Spq，p表示方向，q表示大小，则有：

Spq={S11,S12,…,S1p,S21,…，Spq}

(7)

2.2 权重自适应的多方向形态滤波器

在进行形态滤波去噪时，根据周期性噪声的特点，尝试采用同一方向的结构元素按照从小到大的顺序构成类似于串联电路的串行滤波器。即对含有噪声的图像先使用较小的线性结构元素进行形态学开-闭滤波和形态学闭-开滤波，然后再将滤波结果用较大的线性结构元素进行同样的处理。最后得到串行滤波输出图像。

同理，将不同方向的线性结构元素所构成的串行滤波器构成类似于并联电路的并行滤波器，再通过自适应权值算法构建权重自适应的复合级联滤波器，如图1所示。

图中，输入图像f(x,y)经过某个方向的结构元素进行串行滤波的结果为gi(x,y),i=1,2,…,p，输出图像为G(x,y)，a1,a2,…,ap为p个方向的结构元素的权值。权值可以使用串行滤波的结果图像与含有噪声的原始图像进行差值计算的方式来确定，输出图像通过对串行滤波的结果进行加权求和的方式来得到，则有：

(8)

(9)

3 实验结果与分析

为验证文中复合级联滤波去噪算法的有效性，选择一幅人脸图像，加入周期性噪声及混合噪声，通过构建不同的串、并复合级联滤波器来进行去噪实验。同时，为验证文中算法的优越性，分别使用均值滤波、中值滤波及高斯低通滤波进行对照。

为了对去噪后的图像质量进行评价，引入两个定量评价的指标：峰值信噪比(PSNR)和结构相似性(SSIM)。

PSNR是一种全参考的图像质量评价指标，评估去噪后的图像与原始图像的接近程度，值越大，则去噪效果越好[16]。若原始图像为Y，去噪后图像为X，图像的大小为M*N，则PSNR定义如下：

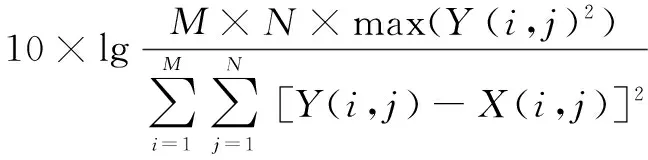
(10)

SSIM是一种衡量两幅图像相似度的指标。若原始图像为x，去噪后图像为y，这两张图像的结构相似性可按照以下方式求出[17]：

(11)

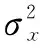
3.1 周期性噪声去除

实验将最常见的正弦周期性噪声添加到原始图像上，分别使用4种滤波方法去除正弦周期噪声，结果如图2所示。

从图2可以看出，权重自适应的复合级联滤波效果较好，而且较好地保持了图像的几何特征；均值滤波和中值滤波对周期性噪声几乎没有明显的去除效果；高斯低通滤波能很好地去除周期性噪声，但图像变得模糊、图像灰度发生较大变化、几何特征有所改变。

图2 周期噪声滤波的结果

图3(a)为4种滤波结果的PSNR曲线。可以看出，文中算法比均值滤波、中值滤波及高斯低通滤波的PSNR值分别提高了0.585 0、1.802 5及7.715 6，表明文中算法具有比较明显的优势。图3(b)为4种滤波结果的SSIM曲线。可以看出，中值滤波的结果与原图像的相似性最小，而文中算法的结果与原图像最相似，表明文中算法性能较好，这与PSNR值的结果是一致的。

图3 周期噪声滤波的PSNR和SSIM比较

3.2 混合噪声去除

实际生活中的图像可能会同时受到周期性噪声及其他噪声的污染。因此，考虑上面提到的几种滤波方法对混合噪声的去除能力。

图4是对原始图像同时添加ω=30的正弦曲线噪声及密度为0.02的椒盐噪声图像，以及分别使用上述4种滤波方法去除噪声的结果。

图4 混合噪声滤波的结果

图4表明，文中所述的权重自适应的复合级联滤波对混合噪声的滤除效果比较好；均值滤波对周期性噪声和椒盐噪声的去除效果不好；中值滤波能较好地去除椒盐噪声，但对周期性噪声几乎没有明显的去除效果；高斯低通滤波使图像变得模糊。

图5(a)和图5(b)为4种滤波算法对含有混合噪声的图像进行滤波后的PSNR和SSIM比较。可以看出，相较于周期性噪声，文中算法和均值滤波的PSNR有所减小；除了中值滤波，其余3种滤波算法的SSIM都明显减小，表明这几种算法对周期性噪声去除的效果比对混合噪声去除的效果要好。

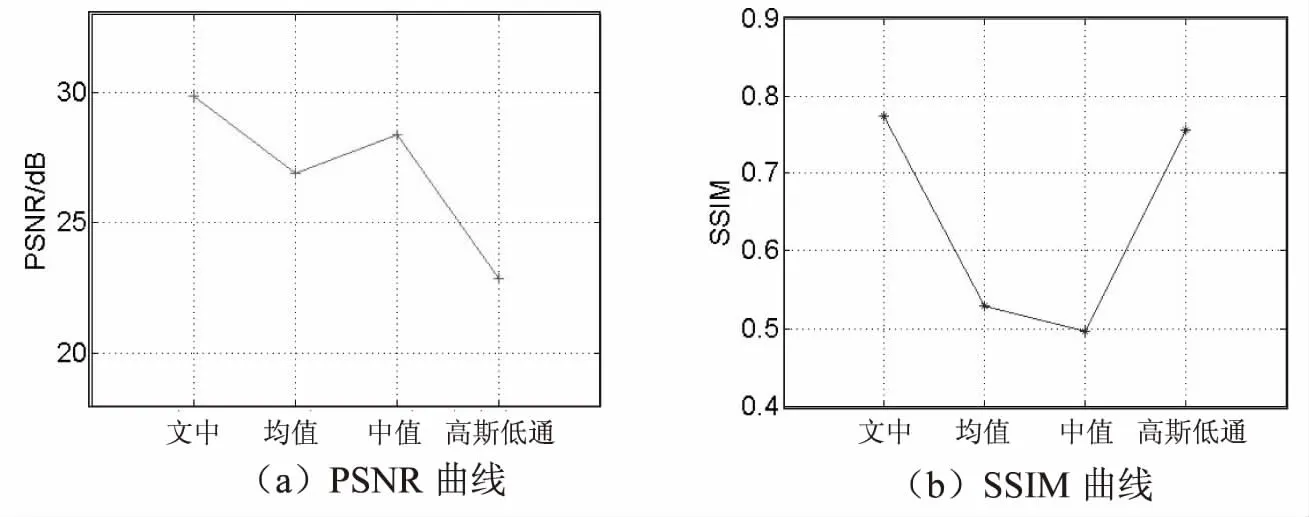
图5 混合噪声滤波的PSNR和SSIM比较

4 结束语

文中使用了不同尺度和方向的结构元素来构建权重自适应的复合级联滤波器，并讨论该滤波方法对周期性噪声及混合性噪声去除的性能。从仿真结果来看，该方法恢复的图像比均值滤波、中值滤波及高斯低通滤波等现有算法具有更高的峰值信噪比和结构相似性，说明该方法在噪声去除及保持图像的几何形状和信息方面有较好的表现。

参考文献:

[1] 李传朋,秦品乐,张晋京.基于深度卷积神经网络的图像去噪研究[J].计算机工程,2017,34(3):253-260.

[2] 王智文,李绍滋.基于多元统计模型的分形小波自适应图像去噪[J].计算机学报,2014,37(6):1380-1389.

[3] 李 彦,汪胜前,邓承志.多尺度几何分析的图像去噪方法综述[J].计算机工程与应用,2011,47(34):168-173.

[4] 黄玲俐.一种改进权重的非局部均值图像去噪方法[J].计算机技术与发展,2016,26(6):16-19.

[5] HUDHUD G A A,TURNER M J.Digital removal of power frequency artifacts using a fourier space median filter[J].IEEE Signal Processing Letters,2005,12(8):573-576.

[6] SILVA R D D,MINETTO R,SCHWARTZ W R,et al.Adaptive edge-preserving image denoising using wavelet transforms[J].Pattern Analysis and Applications,2013,16(4):567-580.

[7] YAROSLAVSKY L,EDEN M.Fundamentals of digital optics[M].Boston:Birkhauser,1996.

[8] SUR F,GRÉDIAC M.Automated removal of quasiperiodic noise using frequency domain statistics[J].Journal of Electronic Imaging,2015,24(1):013003.

[9] AIZENBERG I,BUTAKOFF C.A windowed Gaussian notch filter for quasi-periodic noise removal[J].Image & Vision Computing,2008,26(10):1347-1353.

[10] ZHEN Ji,LI Qi,WU Qinghua.Reducing periodic noise using soft morphology filter[J].Journal of Electronics,2004,21(2):160-162.

[11] PINGEL T J,CLARKE K C,MCBRIDE W A.An improved simple morphological filter for the terrain classification of airborne LIDAR data[J].ISPRS Journal of Photogrammetry & Remote Sensing,2013,77:21-30.

[12] 耿 帅.基于数学形态学的图像去噪[D].济南:山东师范大学,2012.

[13] HEIJMANS H M.Composing morphological filters[J].IEEE Transactions on Image Processing,1997,6(5):713-723.

[14] 赵春晖,孙圣和.一类多结构元素并行复合形态滤波器[J].哈尔滨工业大学学报,1997,29(2):64-67.

[15] 陈 峥.基于Bandelets的周期噪声去除[D].石家庄:河北师范大学,2015.

[16] 江巨浪,章 瀚,朱 柱,等.高密度椒盐噪声的多方向加权均值滤波[J].计算机工程与应用,2016,52(6):204-208.

[17] WANG Zhou,BOVIK A C,SHEIKH H R,et al.Image quality assessment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.