改进的新型蝙蝠算法
吕赵明,张颖江
(湖北工业大学 计算机学院,湖北 武汉 430068)
0 引 言
在许多科学计算中都会遇到最优化问题,最优化问题是通过对无限可行的方案进行寻优从而得到最优的方案。传统的优化算法,如线搜索、非线性搜索、线性规划和整数规划等,对函数有一定要求,对高维、非线性的问题计算复杂度大,在实际工程中不适用。20世纪50年代中期一些研究者摆脱了经典数学优化方法,受生物群体行为特点、觅食方法等机理的启发,提出了仿生智能优化算法,如进化算法、粒子群算法、人工蜂群算法等,对传统算法无法处理的问题可以求解到较好的结果。
Yang Xinshe教授受蝙蝠利用回声定位的能力在黑暗中捕食猎物和躲避障碍物行为的启发,在2010年提出了蝙蝠算法(BA)[1-2]。在对基本的蝙蝠算法进行试验研究后,发现基本蝙蝠算法存在易陷入局部最优、求解精度不高等缺陷。文献[3]通过自适应改变蝙蝠的步长,提高了算法的求解精度。文献[4]把差分进化算法应用到蝙蝠算法中,提高了算法的性能。文献[5]提出每只蝙蝠动态自适应地调整自己的飞行速度和方向,不仅提高了全局搜索性能,而且有效避免了过早收敛。
在上述研究的基础上,文中提出了基于细菌觅食算法算子改进的新型蝙蝠算法。为了避免陷入局部最优,融合细菌觅食算法的趋化算子来提高算法的局部搜索能力;为了提高算法的求解精度,增加了试探扰动因子来充分搜索解空间,采用随机惯性权重[6]来平衡算法的探索能力和挖掘能力。
1 蝙蝠算法
基本蝙蝠算法的仿生原理是模仿蝙蝠的回声定位的机制设计的仿生智能优化算法。该算法将空间中捕食的蝙蝠模拟为问题的解,将蝙蝠不断变化的位置模拟为问题函数的适应度值,将蝙蝠捕食过程中不断变化的频率、脉冲速率、音强模拟为解的优化搜索过程,整个群体的运动在问题求解空间中产生从无序到有序的演化过程[1-2]。
具体的仿真数学模型为蝙蝠在d维空间中位置和速度的更新,通过以下公式实现:
fi=fmin+(fmax-fmin)β
(1)
(2)
(3)

xnew=xold+εAt
(4)
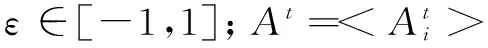
在迭代过程中,一旦蝙蝠发现了猎物,其脉冲发射的响度Ai通常会减小,而脉冲速率ri会相应增加。其调整方式表示为:
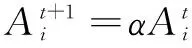
(5)
(6)
其中,α为音强的衰减系数;γ为脉冲速率增加系数。对于任何0<α<1和γ>0的量都有:
(7)
通过多次试验,发现α=γ=0.9效果较好。初始化时每只蝙蝠都应该有不同的音强和脉冲速率,如果新解被更新,它们的音强和脉冲速率将相应更新,也就意味着蝙蝠正在向最优解移动。
基本蝙蝠算法的计算步骤如下:
步骤1:设置算法的基本参数,包括种群大小、空间维数、音强衰减系数α、脉冲频率fi、脉冲速率增加系数γ、最大音强A、迭代次数;
步骤2:初始化蝙蝠种群的位置、速度、脉冲速率ri和音强Ai,计算每只蝙蝠的适应度值,找出当前蝙蝠的最佳位置和适应值;
步骤3:通过式1~3调整频率来更新蝙蝠的位置和速度;
步骤4:根据产生的随机数,如果(rand>ri)对当前最佳解的位置进行随机扰动产生新位置,并计算新解;
步骤5:根据产生的随机数和产生的新解,如果(rand 步骤6:判断新解是否优于全局最优解,若优于全局最优解,则更新最优解和最优蝙蝠位置; 步骤7:判断是否满足最大迭代次数,不满足转步骤3; 步骤8:对结果进行分析输出,算法结束。 细菌觅食算法(bacterial foraging optimization,BFO)[7-9]是K.M.Passino在2002年模仿细菌在人体肠道内寻找食物的行为提出的群体智能算法,该算法有三个算子,分别是趋化算子、繁殖算子、迁徙算子。算法在进行搜索时按照三个算子的执行顺序依次执行,从而使得待求的解不断更新,不断逼近最优解。 趋化算子是算法的核心部分,决定着细菌能否找到食物源,对算法的性能和收敛性有着极其重要的影响。其中包括翻转和前进两种算子,翻转算子表示细菌向任意方向移动的模式;前进算子表示在细菌翻转后,若适应值没有得到改善而沿着同一方向移动若干步,直到达到最大移动次数或其适应度值稳定的模式。相对应的公式如下: Xi(j+1,k,l)=Xi(j,k,l)+rand()×step×Φ(i) (8) (9) 其中,Xi(j,k,l)表示细菌个体i当前的位置,j表示细菌的第j代趋化算子,k表示细菌的第k代繁殖算子,l表示细菌的第l代迁徙算子;step表示前进步长;Φ(i)表示细菌的随机翻滚方向;Xrand(j,k,l)表示当前个体领域内的一个随机位置。 基本蝙蝠算法在寻优过程中,当搜索到近似解后会出现停滞现象,表明此时种群没有进化能力,导致种群多样性受到限制而最终陷入局部最优解,对高维复杂函数问题就会明显地出现寻优精度不高的现象,可见种群的多样性及种群的质量对蝙蝠算法的性能起着决定性作用。基本蝙蝠算法往往是随机初始化一定数量的种群,这样会出现种群的不均匀现象,导致算法陷入局部最优。基本蝙蝠算法在调整自身速度时是通过随机频率、位置差和上一代的速度来更新当前速度的,缺乏对父代速度继承的特性,这样算法缺乏均衡搜索的能力。从算法的步骤4和步骤5可以看出,蝙蝠发现猎物后,若适应值和音强没有同时减小,则当前蝙蝠的适应度值不改变,另外若适应值没有当前最小适应值优,则丢弃该位置,这样可能跳过邻近最优解[10-15]。 基于以上分析,文中采用细菌觅食算法的趋化算子来改善种群的均匀度,提高种群的质量,从而改进蝙蝠算法的局部搜索能力;增加随机惯性权重来提高蝙蝠对父代的继承性,从而均衡搜索能力;增加试探扰动因子来提高算法搜索的充分性和求解精度。 为了改善种群的均匀度,提高种群的质量,融合细菌觅食算法的趋化算子。细菌觅食算法的趋化算子是细菌躲避有害区域向食物源区域聚集的行为。趋化算子又包括翻转算子和前进算子,翻转算子是通过先将每只细菌进行翻滚,使其向一个随机方向前进一个步长后判断适应值是否得到改善,若适应值得到改善,则细菌继续在这个方向上前进指定的步数,若此时细菌的适应度值不再改善或达到了指定的步数,则算法结束[8]。由此可见,前进算子使细菌个体在自己的领域范围进行了深度的寻优搜索,这样在领域内能找到更加优秀的解,从而增强了算法的局部搜索能力。在经过趋化算子后,每个个体都靠近了食物丰富的区域,改善了最初的位置,就整个群体来看,整个种群得到了均匀化,提高了整个群体的质量。 趋化算子的搜索步骤如下: 步骤1:根据式8和式9计算翻转算子; 步骤2:判断群体的适应度值是否得到改善; 步骤3:若得到改善,群体执行前进算子; 步骤4:判断群体的适应度值是否得到改善; 步骤5:若得到改善,判断是否达到指定的最大前进次数,若没有达到跳转到步骤3; 步骤6:判断趋化算子的执行次数,若达到,算法结束并输出优化后的群体,否则跳转到步骤1继续执行。 为了提高蝙蝠对父代的继承性,从而均衡搜索能力,使用下面的速度调整公式: (10) w=μ+σ*N(0,1) (11) μ=μmin+(μmax-μmin)*rand(0,1) (12) 其中,μmax,μmin为随机权重平均值的最大值和最小值;σ为随机权重的方差;N(0,1)为标准正态分布的随机数。 为了提高算法搜索的充分性和求解精度,在蝙蝠更新位置后若不满足局部搜索或飞向猎物的条件,对当前的蝙蝠进行试探扰动,保持蝙蝠在邻域内的游动状态,而不是根据速度公式飞到下一个位置,根据试探扰动的新位置的适应度值试图更新当前最佳位置及最优值。若适应值未得到改善,说明原蝙蝠(位置更新前的蝙蝠)寻优能力差,因此再通过试探扰动因子更新原蝙蝠位置,在下次迭代过程中由更新后较优的位置为起点继续搜索。这样不仅确保了蝙蝠的灵活性而且增加了搜索的全面性和求解的精度。其试探扰动因子公式如下: (13) (14) 其中,u×rand(1,d)为试探扰动因子,u为[0,1]之间的随机数,d为维数。 综上所述,新型蝙蝠算法的计算步骤如下: 步骤1:设置算法的基本参数,包括种群大小、空间维数、音强衰减系数α、脉冲速率增加系数γ、最大音强A、最大迭代次数等; 步骤2:初始化蝙蝠种群的位置和速度、脉冲速率; 步骤3:根据式8和式9对蝙蝠群体执行趋化算子; 步骤4:计算每只蝙蝠的适应度值,找出当前蝙蝠的最佳位置和适应值; 步骤5:通过式1、式3和式10调整频率来更新蝙蝠的位置和速度; 步骤6:根据产生的随机数,如果(rand>ri)对当前最佳解的位置进行随机扰动,产生新位置,并计算新解; 步骤7:根据产生的随机数和新解,如果(rand 步骤8:若步骤7不成立,则根据式13对当前蝙蝠进行试探扰动并计算新解,若新解优于当前最优解,则更新蝙蝠当前位置和最优解,否则根据式14进行试探扰动,更新原蝙蝠位置; 步骤9:判断是否满足最大迭代次数,不满足转步骤5; 步骤10:对结果进行分析输出。 实验采用Windows7 64位操作系统,处理器为Intel(R)Core(TM)i3-2120 3.30 GHz,内存4 G,编程实验环境为MatlabR2013a。 为了验证改进的新型蝙蝠算法(WRBFBA)的寻优性能,与基本的BA算法和基本的粒子群算法进行对比,从经典的测试函数中选取5个不同维数的函数进行实验,如表1所示。 表1 标准测试函数实验参数 群智能优化算法的初始参数设置对算法的优化性能起着关键作用,因此为了验证算法的可比性,分别对WRBFBA算法、基本BA算法和基本PSO算法的初始参数进行一致性设置: 每种算法的种群数都设置为s=40,迭代次数为300,趋化算子次数Nc=40,最大前进次数Ns=5,独立运行20次。对基本的BA算法,蝙蝠的频率范围f∈[0,2],初始脉冲速率r0=0.75,脉冲速率增加系数γ=0.9,最大脉冲音强A=0.7,脉冲音强衰减系数α=0.9。WRBFBA算法基本参数同BA算法一致,其中趋化算子中步长c=0.000 5,随机权重平均值的最大值mean_max=0.9,随机权重平均值的最小值mean_min=0.4。在PSO算法中学习因子c1=c2=2,惯性权重ω=0.5、σ=0.2。 表2是分别使用算法WRBFBA、PSO和BA对5个测试函数进行实验得到的结果。可以看出,WRBFBA算法在函数的最优值、最差值、平均值和标准差这四个指标中对四个高维复杂函数的寻优精度比BA算法和PSO算法高;对于f2f4和f5这样具有较多的局部最小值的函数,WRBFBA算法搜索到的最优值比BA算法和PSO算法精度高并且f5搜索到最优值-1。对于f3这样很难辨别搜索最优值方向和搜索到全局最优值的函数,算法WRBFBA的寻优结果比BA算法和PSO算法得到的寻优结果误差较小。 表2 三种算法实验结果对比 从图1~4每种算法的收敛情况可以看出, WRBFBA算法快速向下收敛,明显比BA算法和PSO算法收敛速度快;BA和PSO算法收敛到一定值后基本保持不变的趋势;由此可见改进的新型蝙蝠算法不仅避免了陷入局部最优解,而且提高了算法的收敛速度和寻优精度。 图1 三种算法对函数f1的收敛曲线 图2 三种算法对函数f2的收敛曲线 图3 三种算法对函数f3的收敛曲线 图4 三种算法对函数f4 的收敛曲线 针对基本蝙蝠算法存在的问题,提出采用细菌觅食算法趋化算子改进蝙蝠种群的多样性和质量,从而改进蝙蝠算法的局部搜索能力,利用试探扰动因子来提高算法的求解精度和充分性,采用随机惯性权重来均衡算法的探索能力和挖掘能力。实验结果表明,提出的新型蝙蝠算法比基本的BA算法和PSO算法的寻优性能有明显的提高。下一步将对蝙蝠算法参数设置理论及实际的应用进行研究。 参考文献: [1] YANG Xinshe.A new metaheuristic bat-inspired algorithm[C]//Studies in computational intelligence.Berlin:Springer,2010:65-74. [2] GANDOMI A H,YANG Xinshe,ALAVI A H,et al.Bat algorithm for constrained optimization tasks[J].Neural Computing & Applications,2013,22(6):1239-1255. [3] 张宇楠,刘付永.一种改进的变步长自适应蝙蝠算法及其应用[J].广西民族大学学报:自然科学版,2013,19(2):51-54. [4] 肖辉辉,段艳明.基于DE算法改进的蝙蝠算法的研究及应用[J].计算机仿真,2014,31(1):272-277. [5] WANG Xiaowei,WANG Wen,WANG Yong.An adaptive bat algorithm[C]//9th international conference on intelligent computing theories and technology.Nanning,China:[s.n.],2013:216-223. [6] 龚 纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,2012:163-179. [7] PASSINO K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems,2002,22:52-67. [8] 杨淑莹,张 桦.群体智能与仿生计算:Matlab技术实现[M].北京:电子工业出版社,2012:196-200. [9] DAS S,BISWAS A,DASGUPTA S,et al.Bacterial foraging optimization algorithm:theoretical foundations,analysis,and applications[M]//Foundations of computational intelligence.[s.l.]:[s.n.],2009:23-55. [10] PAN T S,KIEN D,NGUYEN T T,et al.Hybrid particle swarm optimization with bat algorithm[C]//Proceeding of the eighth international conference on genetic and evolutionary computing.Nanchang,China:[s.n.],2015:37-47. [11] WANG Yong,CAI Zixing,ZHOU Yuren,et al.Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique[J].Structural and Multidisciplinary Optimization,2008,37(4):395-413. [12] 伊进田,刘云连,刘 丽,等.一种高效的混合蝙蝠算法[J].计算机工程与应用,2014,50(7):62-66. [13] 王 丽,王晓凯.一种非线性改变惯性权重的粒子群算法[J].计算机工程与应用,2007,43(4):47-48. [14] 盛孟龙,贺兴时,王慧敏.一种改进的自适应变异蝙蝠算法[J].计算机技术与发展,2014,24(10):131-134. [15] LAAMARI M A,KAMEL N.A hybrid bat based feature selection approach for intrusion detection[M]//Bio-inspired computing:theories and applications.Berlin:Springer,2014:230-238.2 细菌觅食算法
3 新型蝙蝠算法

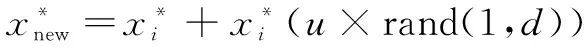
4 实 验
4.1 实验环境和测试函数

4.2 实验参数设置
4.3 实验结果及分析





5 结束语

