基于加速度和角速度的羽毛球动作识别研究

文/吴可涵 吴端坡 陈婷 陈柏平 范剑琪

1 概述

在运动中采集数据，并将数据进行分析完成动作识别是近几年体育产业智能化的热点。基于运动识别的产品和服务也逐渐普及。通过用户运动产生的数据来识别用户运动的动作、状态、运动量等数据，并根据这些信息反馈给用户一些合理的健康运动建议是目前市场的主流。

动作识别主要有两种研究方向，一是基于惯性传感器的动作识别，比如文献[1]使用三轴加速度传感器采集用户动作数据，基于隐马可夫模型针对时间序列建模实现手势识别。文献[2]基于三轴加速度传感器采集数据，利用主成分分析进行人体动作识别。另一种是采用视频监控，运用图像处理的方式进行动作识别，比如文献[3]中针对复杂环境，使用深度图像技术进行手势识别，手势平均识别率可达98.4%。

传统羽毛球赛场上运用摄像设备监控运动员运动以捕获人体姿势，通过图像处理进行分析。由于这种方式需要高质量的摄像设备和复杂的图像处理，动作识别的周期长，成本高，不适用于日常羽毛球运动。

本文给出一种基于加速度和角速度传感器的羽毛球动作识别方法。比起传统的视频监控，图像处理的方法，本文提出的方法成本低，速度快，可移动，适用于用户日常的羽毛球运动。

本文基于MPU9250九轴传感器设计了数据采集模块，该模块体积小，质量轻，使用便捷，适用于羽毛球运动爱好者日常运动。通过采集用户运动时挥拍的加速度和角速度信号，经过信号预处理后，通过滑动窗口检测进行挥拍捕捉并提取动作的特征参数，构建特征向量代入基于马氏距离的羽毛球击球动作判别算法进行动作识别。

2 数据采集模块

本课题组设计实现了一套可用于穿戴羽毛球动作数据采集的硬件系统，如图1所示。

该系统基于MPU9250九轴传感器，通过IIC协议与主MCU控制单元之间进行数据通信和连接。MPU9250采集三轴加速度、三轴角速度信号。其中三轴角速度采样速率最高8KHz，三轴加速度采样速率最高4KHz。MPU9250采集数据经模/数转换器后通过IIC接口传输于MCU，再由MCU主控制器通过UART端口发送的蓝牙模块，实现与移动端的数据传输。系统整体上精简，模块体积大小为27mm×30mm，可放置于羽毛球拍底部，质量为22克，不影响用户运动体验。此外整个系统具备低功耗的特点，整体功耗较小。实测使用3伏纽扣电池作为供电电源，可持续使用2个小时以上，满足用户运动时长需要。

3 动作信号识别系统

3.1 系统整体结构设计

基于加速度和角速度的羽毛球动作识别系统的设计如图2所示。

将数据采集模块传感器装置于羽毛球拍底部。模块的采样频率为10Hz，运动中获取的模拟信号通过模/数转换变成数字信号，导入动作识别系统。经过数字滤波和特征值计算完成信号预处理，再使用活动窗后检测进行挥拍捕捉以提取特征值，合并所有挥拍动作的特征值构建特征向量，将特征向量代入动作识别算法进行判别。

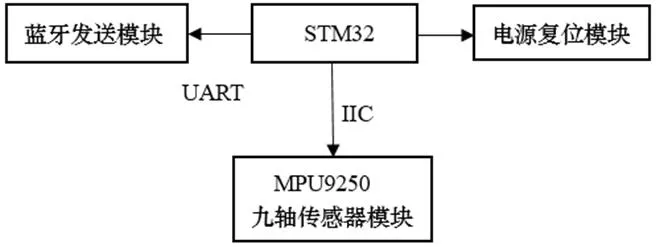
图1：可穿戴羽毛球动作数据采集模块

3.2 信号预处理

3.2.1 数字滤波

羽毛球动作的加速度、角速度信号主要为低频信号。本文采用的信号采集设备频率为10Hz，根据奈奎斯特采样定理，采集的信号最高频率为5Hz。而信号在激励、检测、传输的过程中会受到噪声的影响，同时，运动过程中球拍的抖动也会引入干扰噪声。所以，必须对动作信号进行滤波以去除高频噪声的干扰。本文采用双线性变化法设计Butterworth低通IIR数字滤波器对信号进行滤波。

3.2.2 特征值计算

在实际运动中，球拍的使用不分方向。因此，具有方向的三轴加速度信号和三轴角速度信号直接作为动作的特征值不合理。不妨计算合加速度信号和合角速度信号以排除动作方向的干扰。考虑到挥拍瞬间产生较大的加速度和角速度，不妨计算加速度信号的方差以观测不同动作。综上，本文以合加速度信号、合角速度信号和加速度信号的方差作为特征值，构建特征向量。

因此，记第t时刻采集到的三轴加速度信号 为 axt，ayt，azt， 三 轴 角 速 度 为 jxt，jyt，jzt。分别计算t时刻的合加速度At，加速度方差Dt，合角速度Jt。计算公式如下：

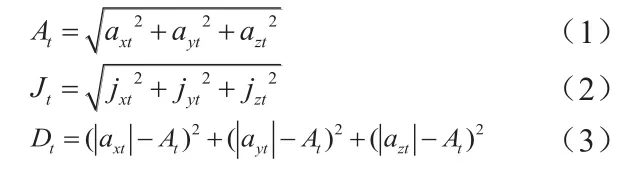
3.3 挥拍捕捉：活动窗口检测

羽毛球运动是连续的，但动作识别需要将动作独立出来单个分析。在羽毛球运动中，一个回合至多挥拍一次，之后会停顿较短时间，而挥拍时加速度和角速度会有较大的起伏，可以利用此特点在连续的加速度数据流中检测可能包含挥拍动作的数据段。

本文通过设置门限阈值自动检测挥拍动作窗口。没有挥拍时，采集到的数据流相对稳定，当做出挥拍动作时，加速度和角速度数据明显变化。设D(t)为t时刻采集计算得到的合加速度方差，U为设置的门限阀值，将D(t)与前后m个采样点逐个进行比较，若：

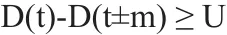
则t时刻的采样点可判断为挥拍数据点。通过滑动检测窗口，合并相邻的连续挥拍动作点，即可检测出可能包含运动信息的数据段。图3是采集的连续运动数据流，虚线为检测出的挥拍动作窗口，表示单次挥拍动作的数据段。

在实际数据处理中，可根据不同用户动作幅度不同设置不同阀值。而羽毛球挥拍周期在一秒至二秒之间，所以窗口宽度m可以取10-20。

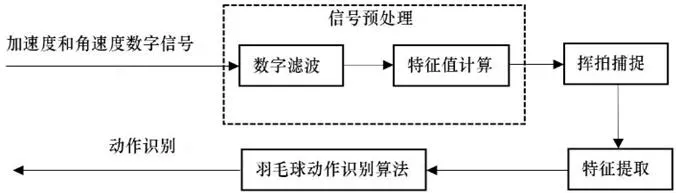
图2：动作信号处理整体结构

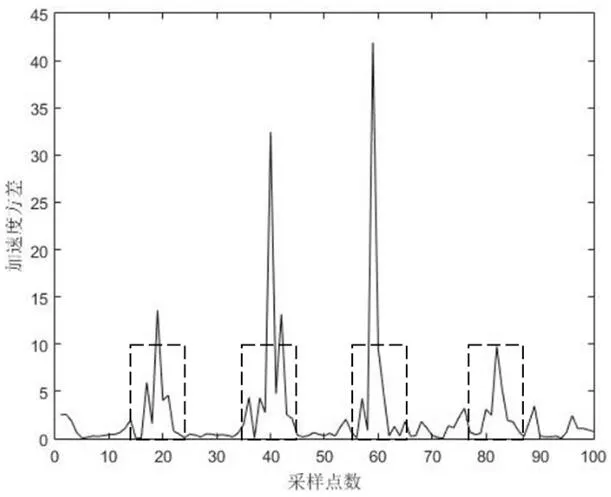
图3：挥拍动作活动窗口检测

图4：可穿戴羽毛球动作数据采集模块

3.4 特征值提取

运动过程中，加速度和角速度是连续变化的，但动作识别需要针对某一次单个数据段进行分析。由于活动窗口检测到的每一次挥拍动作数据段内都存在最大值。在排除了方向对数据的干扰基础上，数据段内的最大值点可以作为某一次挥拍动作的特征值。因此，本文在滑动窗口检测的基础上，将符合要求的数据段内的极大值点所对应的时间点视作挥拍动作捕捉点。合并每一个挥拍动作捕捉点的合加速度、合角速度、加速度方差，构建特征向量。得到的合加速度特征向量为CA=[At1, At2,…, Atn]，合角速度特征向量为CJ=[Jt1, Jt2, …, Jtn]，加速度方差特征向量为CD=[Dt1, Dt2, …, Dtn]。

3.5 羽毛球动作识别算法

3.5.1 距离判别算法

距离判别法的主要思想是计算待测向量到各个总体的距离，通过比较距离的大小来确定待测向量属于的总体。

表1：抽球、挑球、挡球动作特征值范围

表2：实验结果

3.5.2 马氏距离

考虑到加速度、角加速度、加速度方差三钟特征值之间的相关性和单位的不同，在进行距离判别算法时，采用的距离可使用马氏距离。

设有n维向量X=[x1, x2, x3,…, xn]T, Y=[y1,y2, y3,…, yn]T,则马氏距离为：

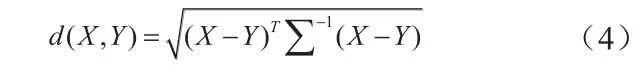
其中 为总体协方差矩阵。

设一个总体G的均值向量 ，总体协方差矩阵为 ，则n维向量X=[x1, x2, x3,…, xn]T与总体G的马氏距离为：

3.5.3 Mahalanobis距离判别

设有n个总体G1, G2,…, Gn每个总体的均值向量为 μ1, μ2,…, μn和协方差∑1,∑2,…,∑n。对于一个新的样本Xi，根据式（2），分别计算样本到每一个总体的马氏距离，记dij(Xi, Gj)为第i个样本到第j个总体的马氏距离。

定义：得到判别准则为：

3.5.4 算法详解

根据马氏距离判别法，本文提出一种基于加速度和角速度的羽毛球动作判别算法。步骤如下：

记G为已知所有挥拍动作为的总体，G包含所有挥拍动作的加速度向量CA，合角速度向量CJ，加速度方差向量CD，得G=[CA,CJ,CD]。

第一步：数据预处理，根据式（1）、（2）、（3）计算所有待识别样本t时刻的合加速度，合角速度和加速度方差。得到合加速度向量XA=[XAt1,XAt2,…,XAtn]，合角速度向量XC=[XCt1,XCt2,…,XCtn]和加速度方差向量XD=[XDt1,XDt2,…,XDtn]；

第二步：根据3.4小节提出的活动窗口检测进行挥拍捕捉。记录该动作的合加速度、合角速度、加速度方差。再根据3.5小节提出的方法提取特征值，合并所有挥拍动作的合加速度、合角速度、加速度方差，得到挥拍动作的合加速度特征向量CA、合角速度特征向量CJ、加速度方差特征向量CD；

第三步：CA、CJ、CD分别和G代入式（5），得到挥拍动作各特征向量与总体特征向量的马氏距离向量dA、dJ、dD；

第四步：将dA、dJ、dD代入式（6），根据式（7）进行判别。

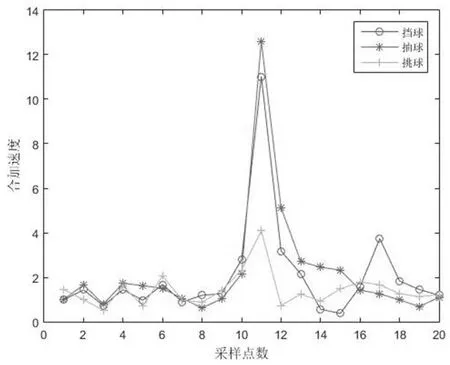
图6：一次抽球、挡球和挑球动作的合加速度

图7：一次抽球、挡球和挑球动作的合角速度

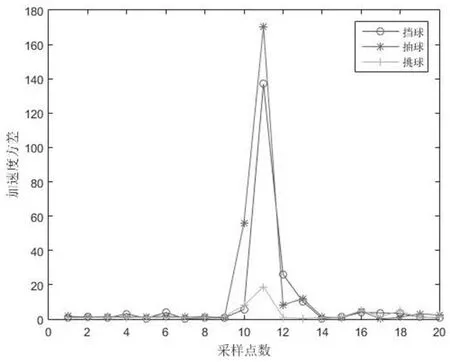
图8：一次抽球、挡球和挑球动作的加速度方差

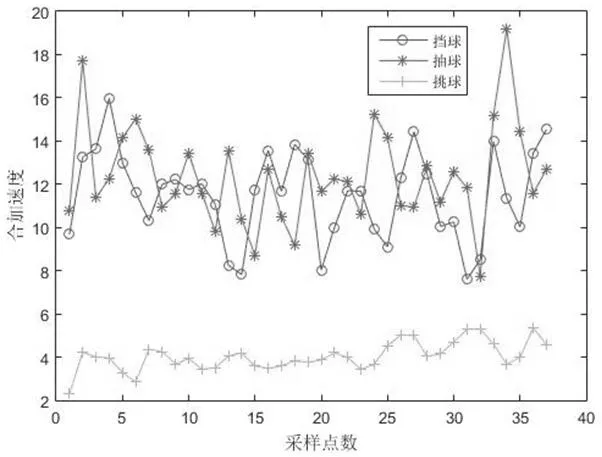
图9：三类击球动作合加速度特征值分布

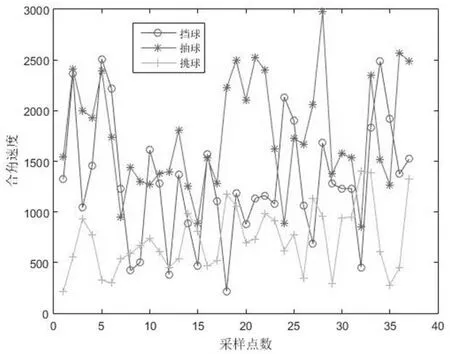
图10：三类击球动作合角速度特征值分布

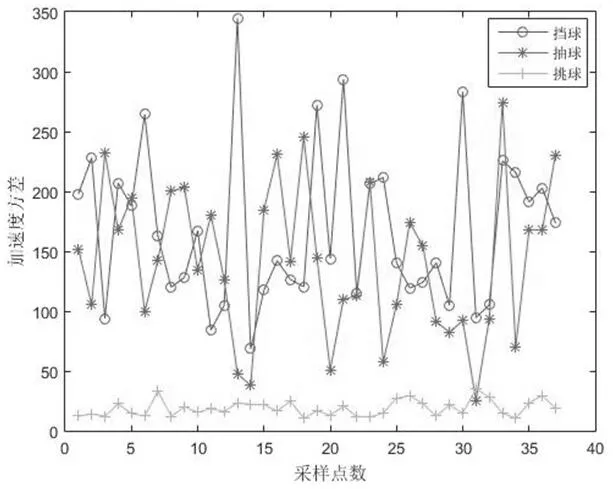
图11：三类击球动作加速度方差特征值分布

4 实验测试与分析

4.1 实验测试

为验证本文羽毛球动作识别算法的有效性，本课题组将数据采集模块(如图4)按图5所示安装于羽毛球拍底部。实际测试中，设置模块信号输出频率为100Hz，采样频率为10Hz。

为获取准确的羽毛球动作测试样本，本项目组要求专业的羽毛球运动员进行抽球、挑球和挡球三个动作的演示，每个动作分别完成若干次，并对击球动作时间进行记录和标记。图6-图8分别为经过活动窗口检测捕捉到的一次抽球、挑球和挡球的合加速度、合角速度及加速度方差三种数据流平均值对比。

4.2 击球动作分析

本文针对运动员完成的抽球、挑球、挡球三种击球动作进行了数据采集和统计，经过数据预处理、活动窗口检测捕捉挥拍动作，计算各动作的合加速度、合角速度和加速度方差三种特征值，得到三类动作的特征值折线图如图9-图11所示。

对比抽球、挡球和挑球动作的三类特征值统计数据，结合文献[16]中关于不同动作具有不同的加速度和角加速度的相关结论，可以得到三类动作的特征值范围如表1所示。

4.3 动作识别算法验证

将4.2小节中经过统计计算得到的各类动作的特征值作为已知总体代入算法；再要求运动员分别完成抽球、挡球、挑球三种击球动作各110次，将数据流作为样本代入算法，得到表2的结果。

算法平均识别率为92.7%，说明本文提出的识别算法能有效识别该三类羽毛球击球动作。

5 总结

本文设计并实现了一套基于加速度和角速度传感器的羽毛球动作识别方案。硬件上，基于MPU9250九轴传感器设计了数据采集模块，使用蓝牙实现数据传输。软件算法上，将采集到的信号先进行滤波，滤除抖动等因素带来的噪声干扰，然后计算合加速度、合角速度以及加速度方差以除去挥拍方向的干扰。再通过窗口检测捕捉挥拍时间点，提取挥拍时间点的合加速度、合角速度以及加速度方差构建特征向量，代入基于马氏距离的动作识别算法进行击球动作识别。本文提出的羽毛球动作识别方案可以自动捕捉用户挥拍的有效动作，解决了挥拍方向对动作识别干扰的问题。经过实验测试，算法对抽球、挑球和挡球三类羽毛球动作的平均识别率为92.7%，能有效识别该三类击球动作。

此外，本文只针对抽球、挑球和挡球三类击球动作进行了实验测试，对于其他羽毛球击球动作依然适用。同时，本文提出的基于加速度和角速度的羽毛球动作识别方法可以推广于其他球拍类运动，例如网球、乒乓球等。

参考文献

[1]刘蓉,刘明.基于三轴加速度传感器的手势识别[J].计算机工程,2011,37(24):141-143.

[2]李锋,潘敬奎.基于三轴加速度传感器的人体运动识别[J].计算机研究与发展,2016,53(03):621-631.

[3]曹雏清,李瑞峰,赵立军.基于深度图像技术的手势识别方法[J].计算机工程,2012,38(08):16-18.

[4]Blanche T J,Swindale N V.Nyquist interpolation improves neuron yield in multiunit recordings[J].Journal of neuroscience methods,2006,155(01):81-91.

[5]陈虹兵,常芬,王雨,黄亚男.基于MATLAB双线性变换法IIR滤波器的设计[J].电脑知识与技术,2016,12(17):215-217.

[6]童晓兵,张玉明,徐以涛.“数字信号处理”课程中双线性变换法的探讨[J].电气电子教学学报,2014,36(02):68-70。

[7]陈哲.高水平羽毛球男单项目比赛时间与击球位置特征分析及研究[D].上海体育学院,2011.

[8]周博翔.基于加速度传感器的人体运动姿态识别[D].长沙理工大学,2014.

[9]洪远泉,周永明,郑春龙.基于距离判别的心电身份识别技术研究[J].科学技术与工程,2014,14(18):252-255.

[10]Deng Zhongmin,Bi Sifeng,Sez Atamturktur.Stochastic model updating using distance discrimination analysis[J].Chinese Journal of Aeron autics,2014,27(05):1188-1198.

[11]Liu W M,Chou K C.Prediction of protein structural classes by modified mahalanobis discriminant algorithm[J].Journal of protein chemistry,1998,17(03).

[12]李玉榕,项国波.一种基于马氏距离的线性判别分析分类算法[J].计算机仿真,2006,23(08):86-88.

[13]Kamoshita T,Tabata K,Okano H,et al. Optimization of a Multidimensional lnformation System Using Mahalanobis Distance[J].Journal of Quality Engineering Society,1998,6(03):91-99.

[14]吴香华,牛生杰,吴诚鸥,秦伟良.马氏距离聚类分析中协方差矩阵估算的改进[J].数理统计与管理,2011,30(02):240-245.

[15]Hajjar C,Hamdan H.Interval data clustering using selforganizing maps based on adaptive Mahalanobis distances[J].Neural Networks,2013,46:124-132.

[16]陈立勋.羽毛球运动员正手搓、推、勾击球动作一致性的生物力学分析[D].北京体育大学,2016.