巧借三角换元 妙解高考试题

☉江苏省张家港市塘桥高级中学 周 浩

换元思想是一种经典的数学思想方法，而三角换元是其中最重要的一种.经常借助三角换元，把题中的相关代数、向量、几何等问题转化为三角问题，选择一些合适的三角函数（或三角函数式）去代换关系式中的变数，由自变量的范围限制角的范围，利用三角函数中的相关知识，将所求问题化归为三角问题，用来解决相关问题中的最值问题或取值范围问题等，是实现解题目标的一种非常有效的转化策略.特别在高考中，经常采用三角换元来解决相应的问题.

一、代数式中的三角换元

例1 （2017年北京卷）已知x≥0，y≥0，且x+y=1，则x2+y2的取值范围是______.

分析：结合条件x+y=1加以三角换元，通过代数式x2+y2的三角变换，利用三角函数的相关公式的转化，结合三角函数的图像与性质来确定其取值范围问题.

点评：解决本题的方法较多，各有特色，各有所长.而根据三角关系式sin2α+cos2α=1，很自然地联想到引入三角元素，采用三角换元，结合三角函数的相关知识来解决问题.

二、向量中的三角换元

例2 （2017年浙江卷）已知向量a，b满足|a|=1，|b|=2，则|a+b|+|a-b|的最小值是______，最大值是______.

分析：结合条件|a|=1，很自然联系起a=（cosα，sinα），进而借助三角换元思想，把相应的平面向量的相关知识转化为三角函数知识，结合三角函数的图像与性质来确定平面向量中的最值问题.

解析：设a=（cosα，sinα），b=（2，0），则a+b=（cosα+2，sinα），a-b=（cosα-2，sinα），

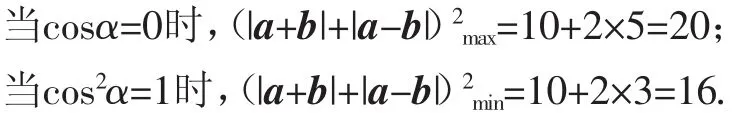
点评：在解决平面向量问题时，往往通过构造平面直角坐标系，根据向量的条件引入三角元素，通过三角换元，结合向量的坐标运算与模运算等来转化为三角关系式问题，结合三角函数的图像与性质来确定最值问题.

三、解析几何中的三角换元

例3（2017年江苏卷）在平面直角坐标系xOy中，A（-12，0），B（0，6），点P在圆O：x2+y2=50上.若P—→A·P—→B≤20，则点P的横坐标的取值范围是______.

分析：根据点P在圆上的条件引入三角元素，设出相应的三角参数坐标，结合平面向量的坐标表示与数量积公式建立不等关系，并结合同角三角函数基本关系式来确定cosα的取值范围，进而数形结合来确定点P的横坐标的取值范围.

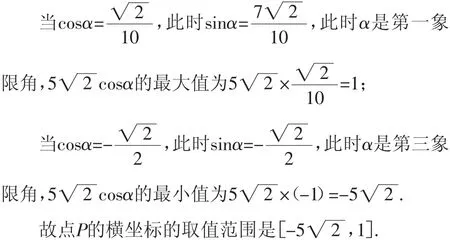
点评：在解析几何中，往往结合直线的方程、圆的方程、圆锥曲线的方程等引入三角元素，结合相应方程的三角参数，把解析几何问题转化为三角函数问题，也是解决一些解析几何中的最值问题比较常见的一种思维方式.

四、实际应用中的三角换元

例4（2017年全国卷Ⅱ）在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系.曲线C1的极坐标方程为ρcosθ=4.

（1）M为曲线C1上的动点，点P在线段OM上，且满足|OM·||OP|=16，求点P的轨迹C2的直角坐标方程；

（2）设点A的极坐标为），点B在曲线C2上，求△OAB面积的最大值.

分析：（1）通过化曲线C1的直角坐标方程，设出点P，M的坐标，通过条件建立关系式，化简即可得点P的轨迹C2的直角坐标方程；（2）根据点B在圆C上引入三角元素，通过三角换元，结合三角形的面积公式转化为三角关系式，进而确定△OAB面积的最大值.

解析：（1）设P的直角坐标为（x，y），曲线C1的直角坐标方程为x=4.因为O，P，M三点共线，则点M的坐标为

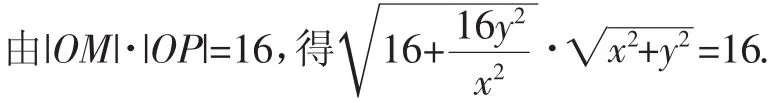
因为x＞0，化简整理可得x2+y2-4x=0（x≠0），

因此C2的直角坐标方程为（x-2）2+y2=4（x≠0）.

（2）在直角坐标系中，点A的坐标为，则直线OA的方程为设点B的坐标为（x，y），则点B到直线OA的距离为

又|OA|=2，则△OAB面积

又点B在圆C：（x-2）2+y2=4（x≠0） 上，可设B（2+2cosα，2sinα），

所以△OAB面积的最大值为

点评：在解决一些相关应用问题中，经常通过借助三角换元思想，依据题设的特殊性，适当引入角参数，由自变量的范围限制角的范围，利用同角关系和三角变化等，将相应的应用问题化归为三角问题来解决，达到目的.

其实，三角换元的优点在于通过对题中条件或结构的有规律的“模式识别”，充分利用题目中的有效信息，积极思考，自主构建合适合理的解题方法，加强对数学化归与转化思想的理解和认识.因此，在教学实践过程中，教师应注重引导学生对问题结构特征的分析和把握，发展学生的认识力，培养学生的创造力，这样对学生的全面解题能力的发展将大有裨益.H