基于中智加权相似度量的尺度自适应视觉目标跟踪算法

胡珂立，范恩，叶军，沈士根，谷宇章

（1.绍兴文理学院，浙江 绍兴 312000；2.中国科学院上海微系统与信息技术研究所，上海 200050）

1 引言

随着“平安城市”的进一步建设以及人们对安全生活、生产需求的进一步提升，以物联网为代表的多项技术不断发展。视觉传感器是物联网感知世界的关键途径，众多视觉传感器产生的海量数据须经编码[1]传输，与视觉传感数据紧密相关的视觉分析[2,3]也是当前最重要的环境感知手段之一。视觉目标跟踪[4-6]的任务为锁定监控区域内兴趣目标，时刻感知其位置信息。视觉目标跟踪是进行后续高级分析任务的重要基础。由于现实场景中面临诸多挑战，提升视觉目标跟踪性能仍是一个挑战性问题。

均值漂移算法由Comaniciu等人[7,8]提出，并被用于视觉目标跟踪。采用颜色直方图作为目标特征。在目标跟踪过程中，算法通过最小化跟踪目标与候选目标区域概率密度函数的距离来确定当前目标位置。由于均值漂移跟踪算法采用颜色直方图特征和高效的目标区域定位策略，能有效地克服运动模糊、目标形变等挑战。然而，当背景区域与目标特征相近时，该算法极易发生偏移，最终导致跟踪失败。鉴于此种问题，一些新的度量方式或特征被引入，例如Cross-Bin度量[9]、SIFT 特征[10]、纹理特征[11]，在一定程度上提升了算法顽健性。Tomas等人[12]将背景信息引入，并提出了基于背景加权的方法。在目标尺度估计方面，Tomas等人[12]采用了前向后向稳定性检测方法，经改进的此均值漂移算法的表现超过了多数性能优异的跟踪算法。此外，在尺度更新方面，Robert等人[13]采用差分尺度空间滤波器的策略，也取得了一定成效。尽管众多学者做了很多努力，但视觉目标跟踪仍是一个开放问题。鉴于均值漂移跟踪算法的高效性，寻求一种恰当的方式以充分利用目标信息和背景信息提升目标位置估计的顽健性仍十分必要。

中智集理论[14]由Smarandache提出，相较于传统的模糊理论，中智集理论除了对真（truth）、假（falsity）分量进行表述外，还专门对不确定（indeterminacy）分量进行了处理。中智集理论在处理不确定信息方面展现出很大优势。为了将中智集理论用于工程领域，参考文献[15]提出了单值中智集的概念，将真、假、不确定分量的值限定在0到1的闭区间范围内。为将单值中智集用于工程决策，参考文献[16]提出了余弦相似量测。鉴于中智理论的有效性，其被广泛用于计算机视觉[17-23]、汽轮机故障诊断[24]、治疗方案选择[25,26]、聚类理论等[17,27-29]。参考文献[17,18,21-23]将中智集理论用于图像分割，其中参考文献[17]提出了中智相似聚类方法；参考文献[18]将不确定滤波器引入图像分割；参考文献[21]引入核约束，提出了核空间中智模糊均值聚类算法。在参考文献[19]中，率先将单值中智集引入视频目标跟踪算法中，提出了面向图像颜色域和深度域的中智真、假、不确定分量的度量方法，并利用单值中智交叉熵完成了颜色和深度空间的信息融合，以此提升了跟踪算法性能。参考文献[30]利用中智相似度量建立新的权值，一定程度上提升了跟踪算法的顽健性，然而其将 3个中智分量同等看待，且采用固定尺度信息，一定程度上限制了算法性能。

本文引入中智加权相似度量，提出了尺度自适应的中智均值漂移视觉跟踪算法，主要贡献如下：

（1）提出了中智分量加权的思路，并将其引入余弦相似度量；

（2）针对帧间目标特征稳定度和目标背景差异性提出了相应属性下的真、不确定、假量测计算方法，并利用加权余弦相似度量建立权值向量；

（3）针对目标尺度自适应更新问题提出了目标尺度缩小/扩大的真、不确定、假量测计算方法，并提出了中智框架下的尺度更新策略。

2 中智余弦相似度量

2.1 单值中智集

单值中智集是中智集的重要组成部分，单值中智集的提出使得中智理论用于科学与工程问题成为可能。单值中智集中每个元素对应的真、不确定和假分量均为实数数值。假定X是一个全集，在X中的单值中智集A可以表示为：

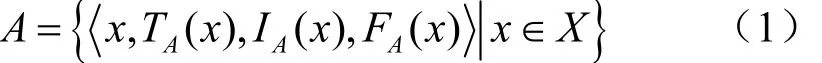
其中，T(x)、I(x)和F(x)分别表示对应元素的真、不确定和假分量量测函数，且TA(x)、IA(x)、FA(x)∈[0,1]，0≤TA(x)+IA(x)+FA(x)≤3。

假定是一个可供选择的集合，是一个条件属性集合，依照式(1)，Ai可以被表示为：

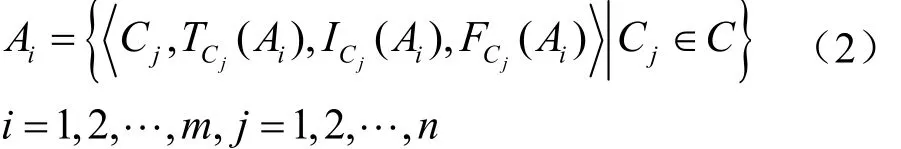
其中，TCj(Ai)、ICj(Ai)和FCj(Ai)是在条件属性Cj下针对Ai的真、不确定和假分量量测函数，且TCj(Ai)、ICj(Ai)、FCj(Ai)∈[0,1]，0≤TCj(Ai)+ICj(Ai)+FCj(Ai) ≤3。多条件属性下的集合A为多属性单值中智集。

2.2 余弦相似度量

参考文献[31]中提出了一种面向多属性单值中智集的余弦（向量形式）相似度量测方法，Ai与Aj在属性Ck下的相似度可以表示为：

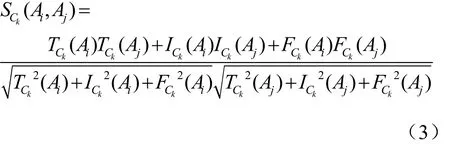
假定A*代表中智集范畴内理想情况下的选择，则任一选择Ai同A*的加权相似度可以表示为：

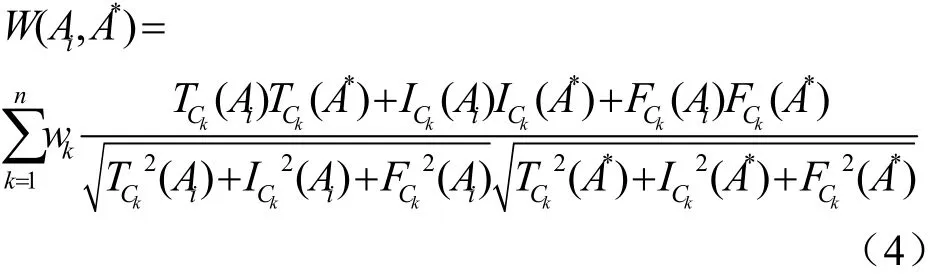
其中，wk∈[0,1]，wk是对应于属性Ck的权值，且

2.3 加权余弦相似度量

观察式（4），可以发现该加权相似度仅是对不同属性的加权，然而在实际应用中，有时须强化各分量内部的T、I、F分量中的一个或多个值。现有的中智相似度量算法并没有这项考虑，因此，将Ai同Aj之间的相似度表示为：

其中，α、β、γ∈[0,1]，分别为T、I、F分量的权值，且满足α+β+γ=1。可以看到，式（5）中的主体部分实际是计算向量和向量之间的余弦值。因此，很容易得出如下3个结论：

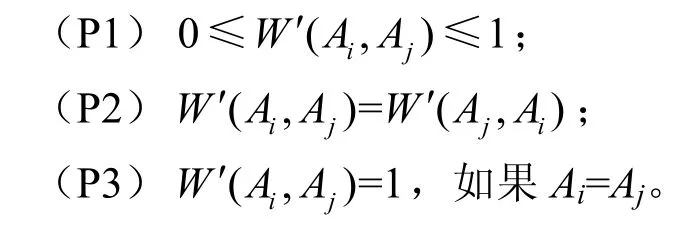
假定A*代表理想选择，则Ai同A*之间的相似度可表示为：

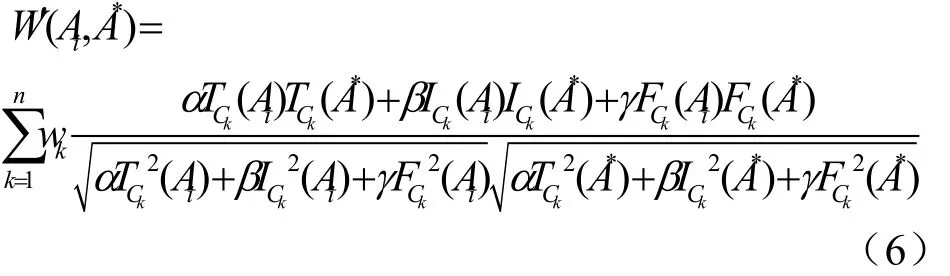
3 权值向量构建

为提升均值漂移跟踪算法的顽健性，本文以目标特征、背景特征为出发点，从帧间稳定度和帧内相似度两个方面对均值漂移跟踪算法进行约束。

3.1 均值漂移跟踪算法

均值漂移算法通常采用核加权颜色直方图，在选定跟踪目标后（通常用矩形框选定目标区域），目标特征被表示为：

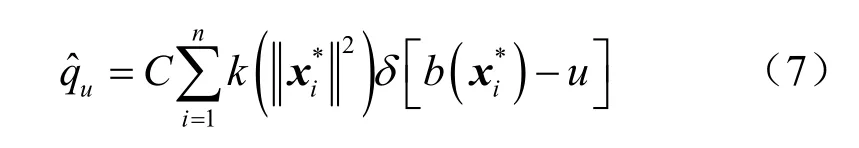
其中，ˆu是直方图的一个分量，假定有m个分量，则有为相对矩形框中心的图像坐标，b(x)是一个映射函数，它将x像素点位置的颜色信息映射在 1～m区间内的某一个数值上。k(x)为核函数，核函数要求具有等向性、凸和单调递减性。δ(x)是克罗内克函数，C为归一化参数，n为目标区域像素点总数。

在跟踪过程中，需要选取候选目标，提取候选目标直方图特征与目标特征比对。假定y是候选目标区域（同尺度矩形框）的中心坐标，候选目标特征可表示为：

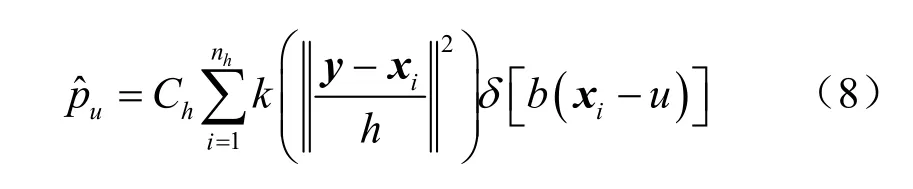
其中，xi为候选区域内的像素点坐标，nh为候选区域总像素点数，Ch为归一化参数。

巴氏相关系数被用来衡量目标特征和候选目标特征的相似度，该相似度被表示为：

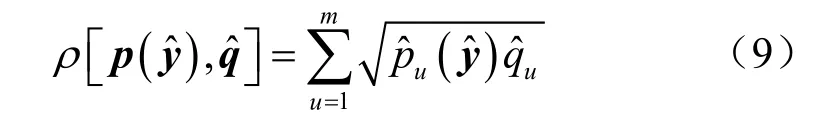
上一帧确定的目标区域通常会被作为下一帧的首个候选目标区域。新一帧目标区域须使得最大。针对该项目标，假设当前候选目标区域中心点图像坐标为0，则下一个候选目标中心点坐标应为[7,8]：

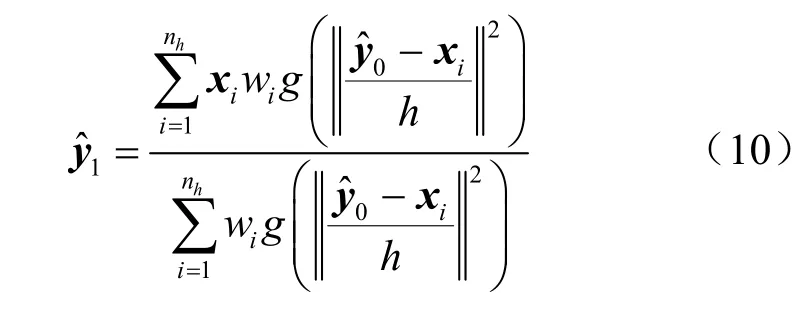
其中，式（10）中的wi可通过式（11）计算：

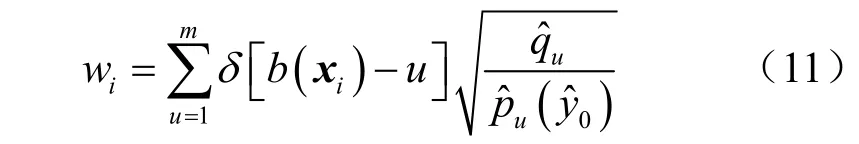
3.2 多属性中智度量

为顽健完成视觉目标跟踪问题，须强化帧间特征较稳定的特征以及和背景特征差异较大的特征。鉴于此，本文以直方图特征每个分量为分析对象，提出了两种基于单值中智集的T、I、F量测。

对于帧间稳定条件属性Cs，借助3σ理论，t时刻的T、I、F量测分别被定义为：

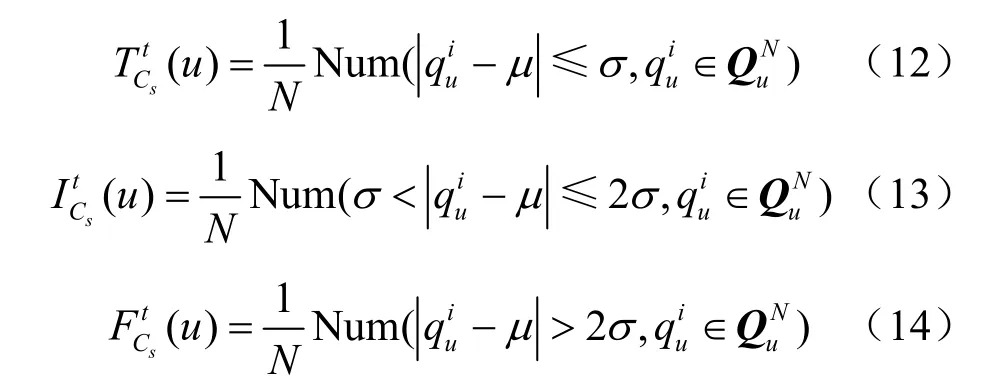
其中，时刻到t时刻目标跟踪位置特征直方图中的第u个分量的集合，μ为该集合的均值，σ为该集合的标准差，N表示该集合中总元素数。可以发现，和分量的含义分别为t时刻前连续N帧时序内满足条件和的u分量数量占总元素数的概率。

对于目标特征强度及目标/背景差异属性Cb，相应的t时刻的T、I、F量测分别被定义为：

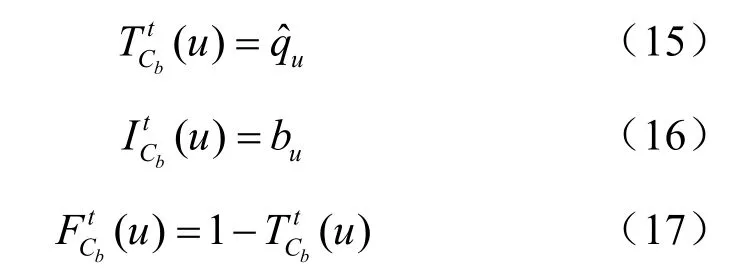
其中，ˆu为目标特征直方图的第u个分量，bu为背景区域特征直方图的第u个分量。在本文中，背景区域被定义为目标区域的等比例外扩区域，两个区域中心均为原目标区域中心。假定目标区域为Go，则背景区域Gb=λGo−Go，λ为扩大系数。bu的计算依据式（7），本文并非在每一帧均更新bu，而是当前帧背景区域特征与bu差异较大时才将其作为新的背景特征。

3.3 权值计算

将式（12）～式（17）代入式（6），便可以得到直方图中第u个分量的中智权值：

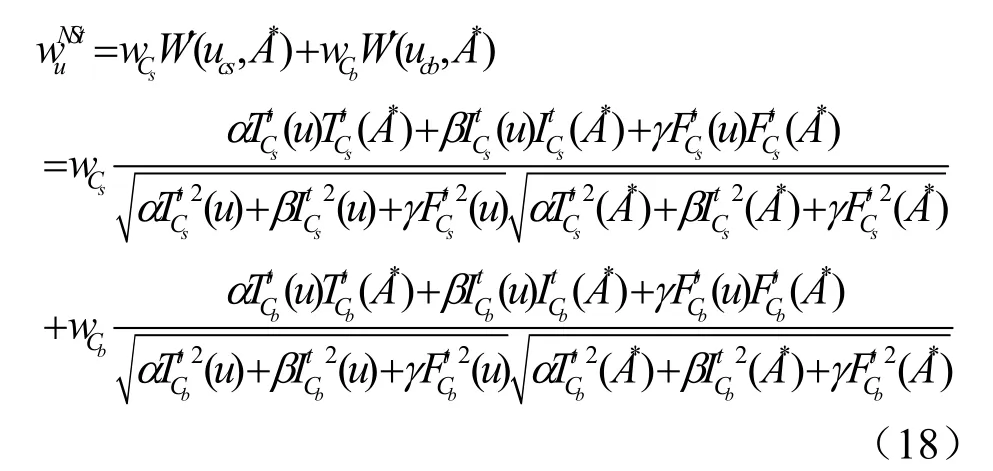
其中分别为两个条件属性对应的权值，此处的理想选择A*在任一属性条件下均被定义为由此，式（18）可以简化为：

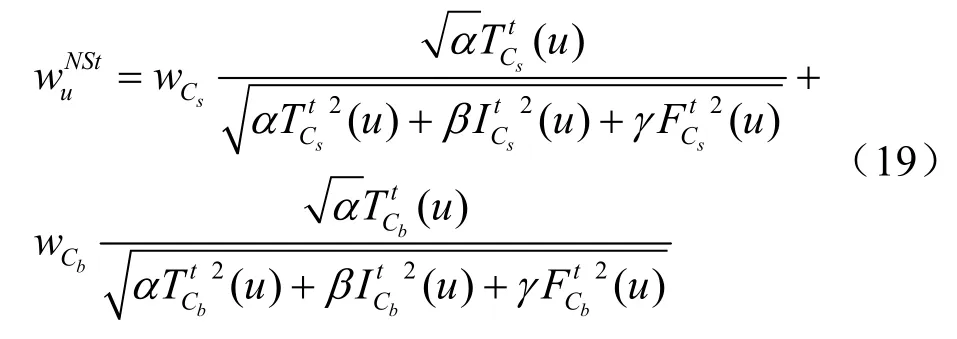
4 尺度自适应方法

在跟踪目标的过程中，目标成像大小可能会发生变化，当跟踪目标框的尺度变化长时间无法适应目标成像尺寸时，易发生跟踪失败。本文将目标候选区域特征与目标特征的相似度作为可靠信息，将目标候选区域特征与背景区域特征的相似度作为不确定信息，首次将中智集理论引入目标尺度更新策略中。

在当前帧目标位置确定后，开始分析是否需要进行尺度更新。首先考虑尺度缩小的情况，基于本文对可靠信息和不确定信息的分析，缩小尺度对应的T、I、F量测分别被定义为：

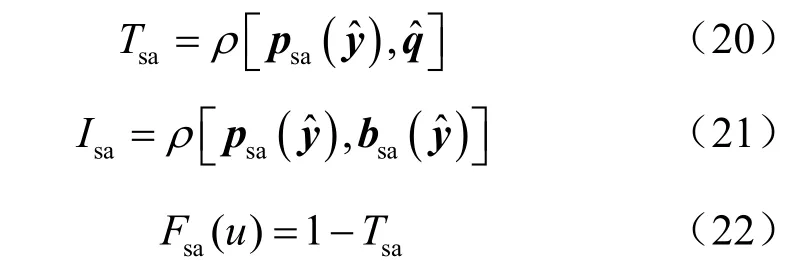
其中，为当前帧目标区域缩小后对应小区域的特征直方图，确定缩小区域的方式与式（16）中背景区域的确定方法类似，同样以当前目标区域为参考，区域中心不变，长宽按同比例缩小λsa倍，λsa为对应的缩放系数。为初始目标直方图。为当前区域对应背景区域的特征直方图。容易发现，Tsa为目标区域缩小后与初始目标特征的相似度，Isa为目标区域缩小后对应背景区域与的相似度。

与式（18）类似，此处的理想选择A*在任一属性条件下也被定义为，将式（20）～式（22）代入式（6），可以得到：

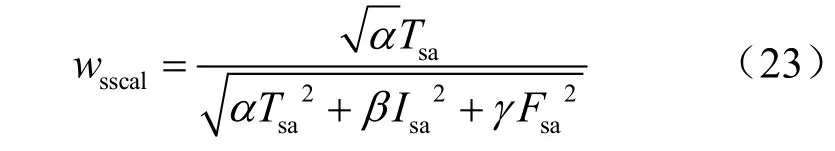
依据同样的策略，可以获得放大尺度对应的中智相似度权值wbscal，其中放大系数为λba。本文取

得到wsscal和wbscal后，可依照式（24）确定当前帧尺度：

其中，s为比例因子，且满足s＞1。该比例因子的设定是为了避免尺度调整过于频繁，或调整时受到噪声干扰。确定λnew后，将目标跟踪框放大λnew倍作为新的跟踪框。

5 中智加权相似度量尺度自适应跟踪算法流程

将本文提出的跟踪算法称为中智加权相似度量尺度自适应均值漂移算法，具体流程如下。

步骤1 在初始帧选取待跟踪目标区域，依据式（8）计算目标特征直方图和初始背景直方图b。

步骤 2 读入新的视频帧。

步骤 3 以上一帧的目标位置作为当前帧目标位置的搜寻起始点0。

步骤 4 以0为起始点，依据式（25）、式（10）和式（19）计算新的目标位置yˆ1。

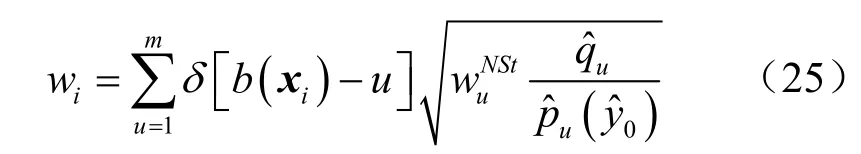
步骤5 若不满足，将重复执行步骤4。

步骤6 依据式（20）～式（24）计算新的目标尺度，更新目标跟踪框。计算当前帧目标背景特征直方图，若

步骤7 输出目标跟踪框，重复执行步骤2～步骤7，直至跟踪结束。

6 实验结果与分析

将本文提出的算法在一些具有挑战性的视频序列中进行了测试，测试序列信息见表1（其中英文缩写含义复杂背景（BC）、快速移动（FM）、运动模糊（MB）、形变（DEF）、光照变化（IV）、平面内旋转（IPR）、低分辨率（LR）、遮挡（OCC）、平面外旋转（OPR）、尺度变化（SV）），共计12 396帧，测试序列中包含了复杂背景、快速移动、运动模糊、形变、光照变化、平面内旋转、低分辨率、遮挡、平面外旋转和尺度变化等挑战。

鉴于提出的算法完全基于均值漂移框架，在选取对比算法时，主要选取了近期基于均值漂移框架表现较优异的算法。为了测试算法性能，将算法与 ASMS[12]、NEUTMS[30]和 KMS[7,8]算法进行了比较。ASMS是近期表现较好的均值漂移框架下的跟踪算法，它在跟踪的同时能够自适应调整尺度信息；NEUTMS是基于中智余弦相似度量的均值漂移算法，其在某些方面的性能已超过了ASMS算法；鉴于本文算法完全基于KMS算法改进，为显示改进效果，也将其引入。除ASMS以外，KMS和NEUTMS在跟踪过程中均不更新尺度信息。为方便阐述，下文以WNEUTSMS表示本文提出的算法。

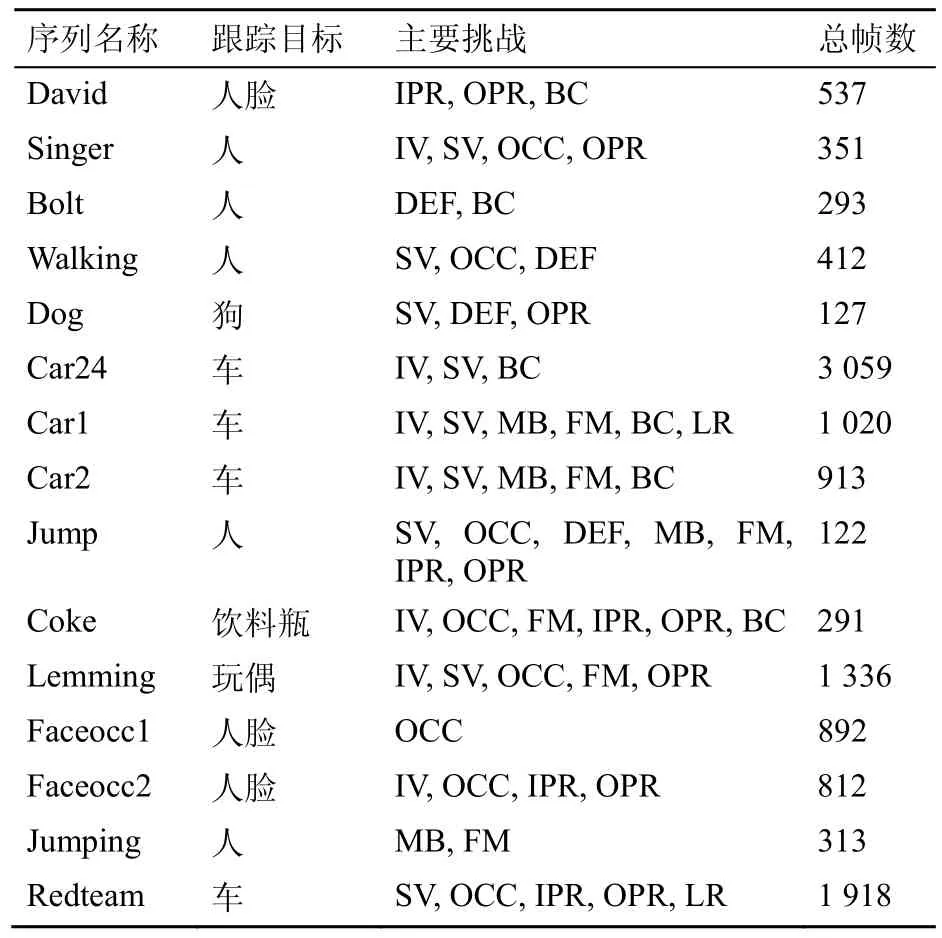
表1 测试视频序列信息

6.1 参数设置

在测试过程中，所设定的参数值均保持不变。计算式（12）～式（14）时涉及的总帧数N被设定为10；计算背景区域时的扩大系数λ被设定为1.6；式（19）中均被设定为0.5，即两类条件属性在权值向量生成时的贡献等分；式（19）、式（23）中的α、β、γ分别被设定为0.5、0.25、0.25，这里适当强化了真分量的贡献；涉及尺度自适应更新过程缩小和放大系数的λbsa和λba均被设定为0.3，式（24）中的比例因子s被设定为1.1；式（24）中的λ0须被设定为一个较小的值，以避免目标框剧烈变化，此处λ0=0.04；算法流程中的ε0和ε1分别被设定为0.1、0.5。

6.2 评价标准

本文主要采用了两种评价方式，一种是中心点误差，该误差是指由算法获得的目标框中心坐标与人为标记的实际目标中心坐标之间的欧氏距离；另一种是跟踪成功率，其测量基准是跟踪目标区域和实际目标区域的重叠度，该重叠度可表示为：

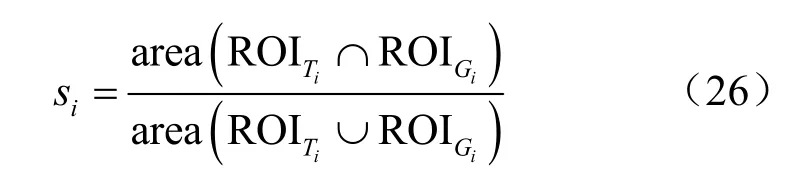
其中，ROITi为第i帧中由跟踪算法获得的目标框区域，ROIGi为第i帧真实目标框区域。通过设定一个最小重叠度r，相应的跟踪成功率可表示为：

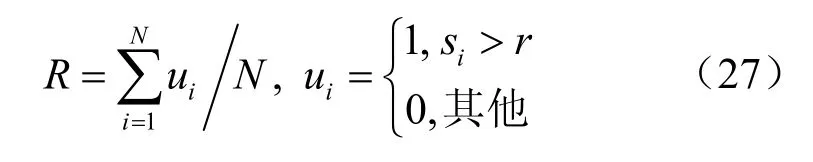
其中，N为视频序列的总帧数。

6.3 目标跟踪结果

图2、图4、图6、图8给出了相应视频序列的跟踪截图，图1、图3、图5、图7给出了对应视频序列跟踪结果的成功率曲线和中心点误差曲线，定量分析了几种算法的跟踪效果。接下来针对各序列展开详细分析。

（1）David序列

图1 David序列跟踪性能曲线

图2 David序列跟踪结果

该序列中各跟踪算法面临的主要挑战包括目标平面内旋转、平面外旋转和相似背景等。从图2可以看到，除了KMS算法，其他3种跟踪算法在前330帧左右表现均较好。在第65帧，受到相似背景区域的干扰，KMS算法发生偏移。从第84帧可以看到KMS算法已失败。在第339帧，可以看到ASMS算法估计了一个过大的尺度，导致目标框较大且开始发生偏移，最终导致跟踪失败（第360帧）。在第430帧中，受背景干扰和目标旋转影响，NEUTMS算法发生了较大偏移。综合图1，可以发现，在此序列中，WNEUTSMS算法表现最好。

（2）Signer序列

该序列中包含的挑战包括光照变化、尺度变化等。从图 4中可以发现，在第 87帧，除了WNEUTSMS和ASMS算法以外，其他算法均已远远偏离了目标位置。从尺度估计上，ASMS在前87帧的表现较好，WNEUTSMS算法给出的目标框相对较小，其原因主要是光照变化导致目标背景发生了剧烈变化，而歌手主体部分仍保持白色主色调，受帧间稳定度约束，目标框锁定在特征较稳定的区域。从第87帧开始，仅WNEUTSMS算法估计的目标位置准确，且在目标特征恢复时能给出恰当的目标尺度（见第274帧、第322帧）。观察图3（b），可以发现虽然ASMS算法的中心位置估计尚可，但其估计的目标尺度远大于目标真实尺寸。综合图3、图4，可以发现，在本序列中，WNEUTSMS算法综合表现最优。

（3）Bolt序列

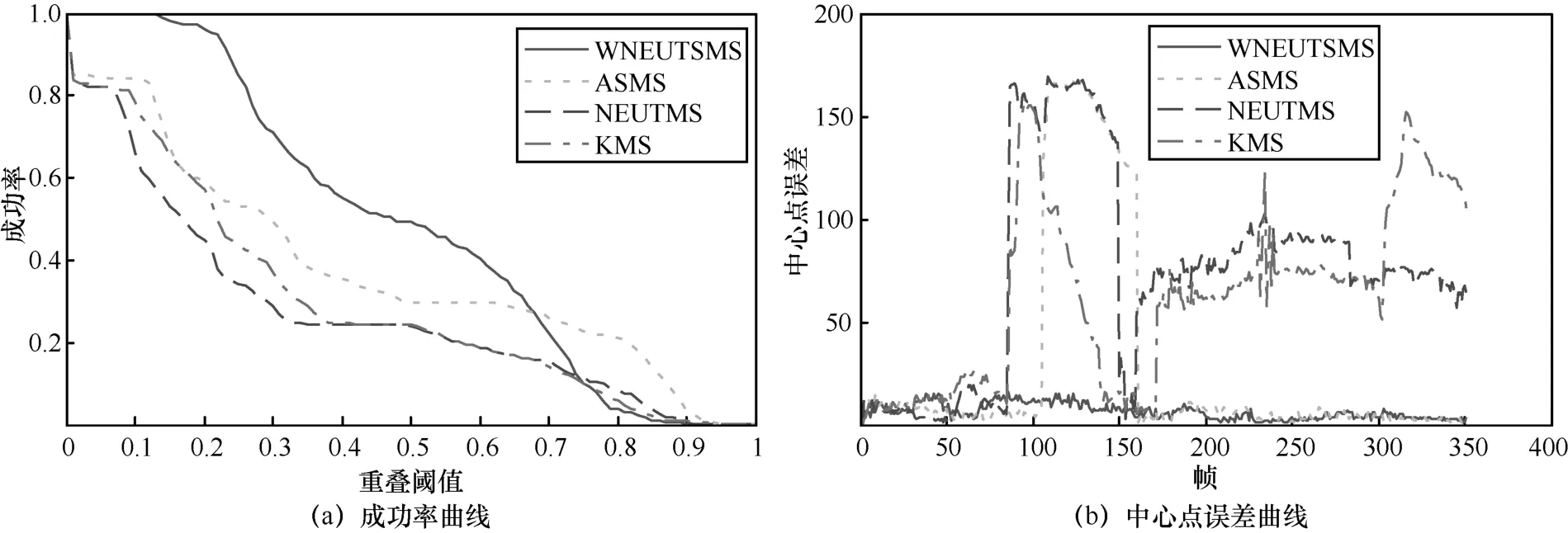
图3 Singer序列跟踪性能曲线

图4 Singer序列跟踪结果

该序列包含的挑战主要有目标形变、复杂背景等问题。观察图5（b），可以发现，从第200帧左右开始，除了 WNEUTSMS算法，ASMS、NEUTMS和KMS算法的跟踪结果均已发生较大偏移，跟踪失败。观察图 6，可以看到在该序列的前半段，4种算法均能较好的完成目标跟踪。在第180帧，算法效果开始出现分化，受 Bolt旁边运动员外观信息干扰，除WNEUTSMS算法外的其他算法受到干扰。借助于尺度估计、帧间稳定特征信息和目标个体特征强化，WNEUTSMS算法较好地完成了目标跟踪。然而，仔细观察后，会发现WNEUTSMS算法估计得到的目标尺度略小于目标成像尺寸，这也是导致在重复率门限较高时，该算法的成功率反而低于其他算法的主要原因。深究造成这一现象的原因，主要是因为目标奔跑速度快、步幅大，导致身体下半部分特征信息极不稳定，故而导致尺度估计偏小。

（4）Walking序列

该序列中主要包含尺度变化、遮挡、目标形变等挑战。观察图7（b），可以发现，相比其他3种算法，WNEUTSMS算法在第 150～170帧、在第200～230帧，在第 250～300帧，均得到了较准确的目标中心点位置。从图8中可以看到，在行人接近车辆之前，各算法表现均较好（见第10帧、第143帧）。在第154帧，因行人本身有不少部分呈现黑色特征，在行人靠近黑色车辆时，4种算法均不同程度上受到黑色车辆的影响，其中ASMS偏离目标中心点最远，WNEUTSMS算法偏离最小，且估计的目标尺寸最接近目标成像大小。从第 153帧起，受背景车辆的干扰，ASMS算法已无法完成尺度信息的准确估计，故而逐步导致算法失败，而WNEUTSMS算法能够给出相对合理的目标框尺寸，这在图7（a）成功率曲线上也有所体现。

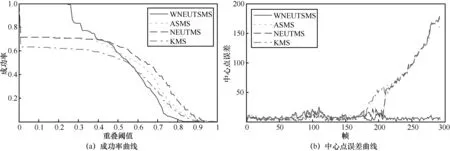
图5 Bolt序列跟踪性能曲线

图6 Bolt序列跟踪结果

为评价本文算法在所有测试序列中的表现，将TRE和OPE评价引入。为完成TRE评价，每个测试序列被分为20份序列片段（各序列片段对应原序列不同起始帧，但均以原序列结束帧为终止），每一个跟踪算法均在每份测试序列片段中进行测试。对于OPE评价，每个测试序列是从第一帧测试到最后一帧，且仅测一次。图9和图10分别给出了基于TRE、OPE评价的面向表1所示整个测试序列集的测试结果，表2和表3分别给出了各跟踪算法应对不同挑战的 TRE-AUC、OPE-AUC分值。AUC分值为成功率曲线中对应成功率曲线与横纵坐标轴围成区域的面积，该值越大，表明算法越顽健。TRE-AUC分值与TRE成功率曲线对应，OPE-AUC分值则与OPE成功率曲线对应。

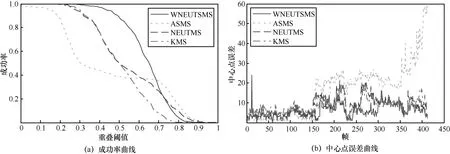
图7 Walking序列跟踪性能曲线

图8 Walking序列跟踪结果

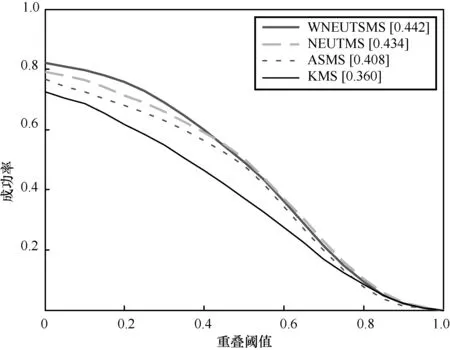
图9 所有测试序列TRE成功率曲线

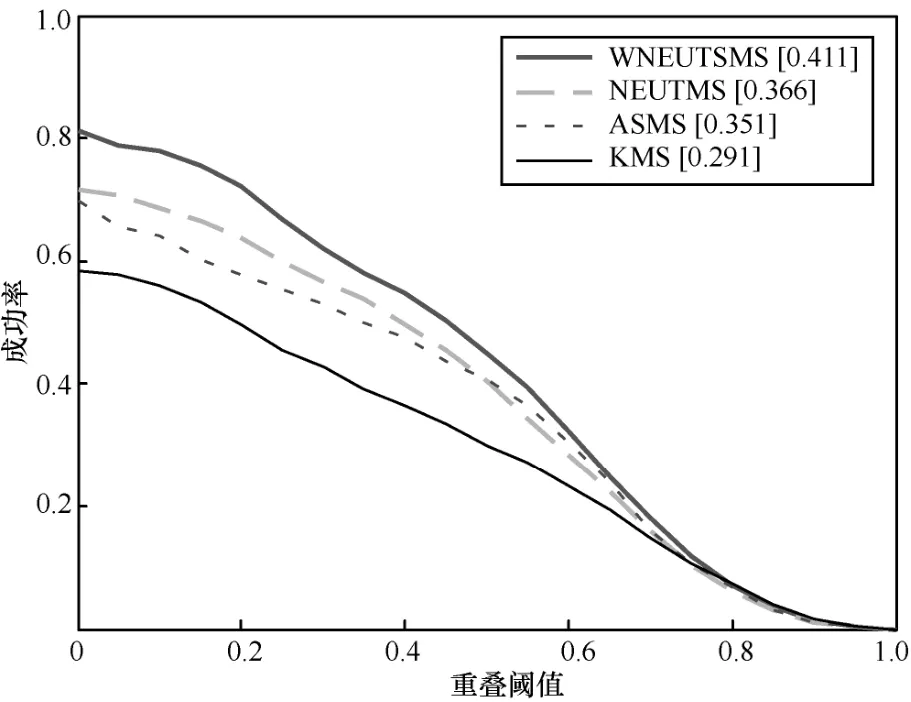
图10 所有测试序列OPE成功率曲线

综合分析图9、图10和表2、表3，WNEUTSMS算法总体表现较好。观察表 2，WNEUTSMS算法在应对复杂背景、光照变化、平面内旋转、遮挡和平面外旋转时表现最好；在应对形变挑战时仅次于NEUTMS算法，其原因主要在于大范围的形变可能会造成目标跟踪框尺度估计不准确；在应对低分辨率和尺度变化时的表现仅次于ASMS算法，其原因主要在于在低分辨率情况下，仅有较少的信息能够被用来提升算法性能。对于OPE评价，WNEUTSMS算法在应对快速移动、运动模糊、形变、平面内旋转、遮挡和平面外旋转时表现最好。在应对复杂背景、光照变化时仅次于ASMS算法。

综合以上分析，可以发现，本文算法（WNEUTSMS算法）在确定目标位置时将目标帧间特征稳定性和背景信息引入，同时强化“真”量测分量；在确定目标尺度时联合考虑目标特征信息和目标背景信息。多类信息融合考量提升了算法在应对背景干扰、光照变化、尺度变化等挑战时的顽健性。

7 结束语

本文提出了一种面向单值中智集的分量加权余弦相似度量，并基于此在中智框架内提升了均值漂移视觉跟踪算法的顽健性。针对目标帧间特征稳定性和目标/背景相似度两种属性，本文提出了相应的真、不确定、假量测计算方式，然后利用分量加权余弦相似度量构建了新的权值向量，用于修正传统均值漂移跟踪算法的权值。此外，本文首次提出了基于中智加权余弦相似度量的尺度更新算法。实验结果表明，本文提出的视觉跟踪算法能较好应对相似背景、光照变化和尺度变化等挑战。

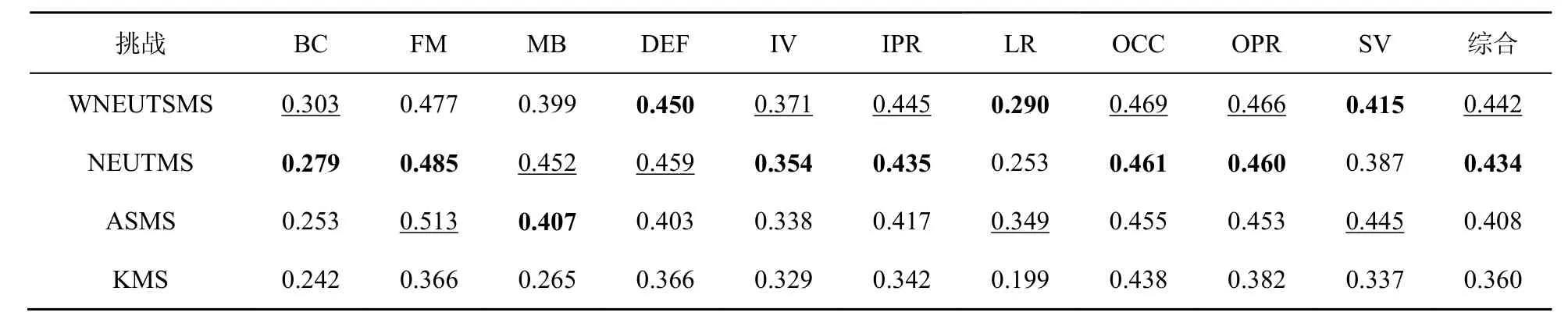
表2 各跟踪算法应对不同挑战的TRE-AUC分值

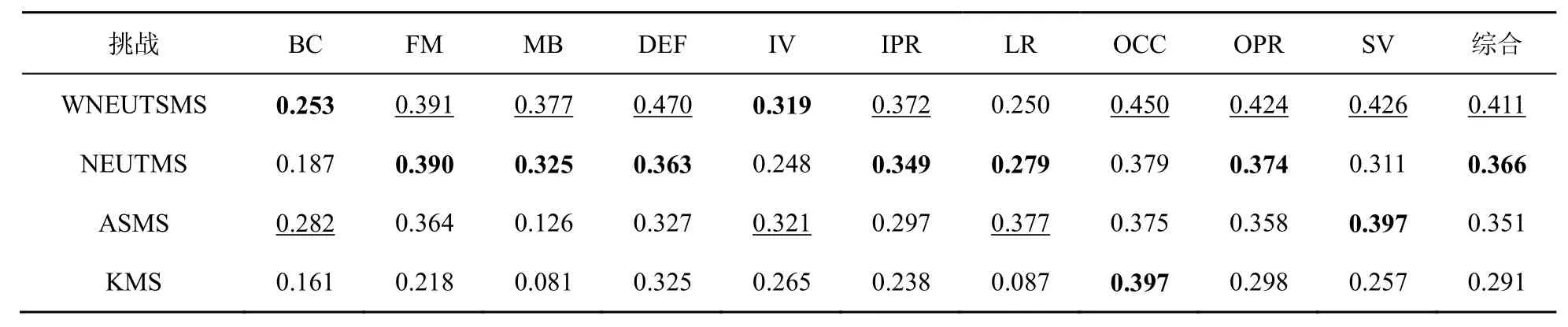
表3 各跟踪算法应对不同挑战的OPE-AUC分值

参考文献：

[1]赵利平, 林涛, 周开伦, 等.一种多色度格式级联编码的AVS2全色度图像编码算法[J].电信科学, 2018, 34(4)： 57-67.ZHAO L P, LIN T, ZHOU K L, et al.A multi-chroma format cascaded coding method for full-chroma image in AVS2[J].Telecommunications Science, 2018, 34(4)： 57-67.

[2]唐彪, 金炜, 符冉迪, 等.多稀疏表示分类器决策融合的人脸识别[J].电信科学, 2018, 34(4)： 31-40.FU B, JIN W, FU R D, et al.Face recognition using decision fusion of multiple sparse representation-based classifiers[J].Telecommunications Science, 2018, 34(4)： 31-40.

[3]颜文, 金炜, 符冉迪.结合 VLAD特征和稀疏表示的图像检索[J].电信科学, 2016, 32(12)： 80-85.YAN W, JIN W, FU R D.Image retrieval based on the feature of VLAD and sparse representation[J].Telecommunications Science, 2016, 32 (12)： 80-85.

[4]YILMAZ A, JAVED O, SHAH M.Object tracking： a survey [J].ACM Computing Surveys, 2006, 38(4)： 13.

[5]WU Y, LIM J, YANG M H.Online object tracking： a benchmark[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 23-28, 2013, Portland, OR,USA.Piscataway： IEEE Press, 2013： 2411-2418.

[6]SMEULDERS A W M, CHU D M, CUCCHIARA R, et al.Visual tracking： an experimental survey [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7)：1442-1468.

[7]COMANICIU D, RAMESH V, MEER P.Real-time tracking of non-rigid objects using mean shift[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 13-15,2000, Hilton Head Island, SC, USA.Piscataway： IEEE Press,2000： 142-149.

[8]COMANICIU D, RAMESH V, MEER P.Kernel-based object tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5)： 564-577.

[9]LEICHTER I.Mean shift trackers with cross-bin metrics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 34(4)： 695-706.

[10]ZHOU H, YUAN Y, SHI C.Object tracking using SIFT features and mean shift[J].Computer Vision and Image Understanding,2009, 113(3)： 345-352.

[11]BOUSETOUANE F, DIB L, SNOUSSI H.Improved mean shift integrating texture and color features for robust real time object tracking[J].The Visual Computer, 2013, 29(3)： 155-170.

[12]VOJIR T, NOSKOVA J, MATAS J.Robust scale-adaptive mean-shift for tracking[J].Pattern Recognition Letters,2014(49)： 250-258.

[13]COLLINS R T.Mean-shift blob tracking through scale space[C]//IEEE Conference on Computer Vision Pattern Recognition (CVPR), June 16-22, 2003, Madison, WI, USA.Piscataway： IEEE Press, 2003： 234-234.

[14]SMARANDACHE F.Neutrosophy： neutrosophic probability,set and logic[M].Rehoboth： American Research Press, 1998：105.

[15]WANG H, SMARANDACHE F, ZHANG Y Q, et al.Single valued neutrosophic sets[J].Multispace and Multistructure,2010(4)： 410-413.

[16]YE J.Vector similarity measures of simplified neutrosophic sets and their application in multicriteria decision making[J].International Journal of Fuzzy Systems, 2014, 16(2)：204-211.

[17]GUO Y, ŞENGÜR A.A novel image segmentation algorithm based on neutrosophic similarity clustering[J].Applied Soft Computing Journal, 2014(25)： 391-398.

[18]GUO Y, XIA R, ŞENGÜR A, et al.A novel image segmentation approach based on neutrosophic C-means clustering and indeterminacy filtering[J].Neural Computing and Applications,2016： 1-11.

[19]HU K, YE J, FAN E, et al.A novel object tracking algorithm by fusing color and depth information based on single valued neutrosophic cross-entropy[J].Journal of Intelligent and Fuzzy Systems, 2017, 32(3)： 1775-1786.

[20]GUO Y, SENGUR A.A novel 3D skeleton algorithm based on neutrosophic cost function[J].Applied Soft Computing Journal,2015(36)： 210-217.

[21]崔西希, 吴成茂.核空间中智模糊聚类及图像分割应用[J].中国图象图形学报, 2016, 21(10)： 1316-1327.CUI X X, WU C M.Neutrosophic C-means clustering in kernel space and its application in image segmentation[J].Journal of Image and Graphics, 2016, 21(10)： 1316-1327.

[22]张桂梅, 王大雷.结合 LPG&PCA 的中智学图像分割[J].中国图象图形学报, 2014, 19(5)： 693-700.ZHANG G M, WANG D L.Neutrosophic image segmentation approach integrated LPG&PCA [J].Journal of Image and Graphics, 2014, 19(5)： 693-700.

[23]郑肇葆, 潘励, 郑宏.中智逻辑图像分割方法的研究与分析[J].武汉大学学报(信息科学版), 2015, 40(2)： 143-146.ZHENG Z B, PAN L, ZHENG H.Research and analysis of neutrosophic logic image segmentation (NLIS) method[J].Geomatics and Information Science of Wuhan University, 2015,40(2)： 143-146.

[24]YE J.Single-valued neutrosophic similarity measures based on cotangent function and their application in the fault diagnosis of steam turbine[J].Soft Computing, 2015,21(3)： 817-825.

[25]MA Y X, WANG J Q, WANG J, et al.An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options[J].Neural Computing and Applications, 2016： 1-21.

[26]YE J, FU J.Multi-period medical diagnosis method using a single valued neutrosophic similarity measure based on tangent function[J].Computer Methods & Programs in Biomedicine,2016(123)： 142-149.

[27]ANTER A M, HASSANIEN A E, ELSOUD M A A, et al.Neutrosophic sets and fuzzy C-means clustering for improving CT liver image segmentation[J].Advances in Intelligent Systems and Computing, 2014(303)： 193-203.

[28]GUO Y, SENGUR A.NECM： neutrosophic evidential C-means clustering algorithm[J].Neural Computing and Applications,2015, 26(3)： 561-571.

[29]GUO Y, SENGUR A.NCM： Neutrosophic c-means clustering algorithm[J].Pattern Recognition, 2015, 48(8)： 2710-2724.

[30]HU K, FAN E, YE J, et al.Neutrosophic similarity score based weighted histogram for robust mean-shift tracking[J].Information, 2017, 8(4)： 122.

[31]YE J.Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment[J].International Journal of General Systems, 2013,42(4)： 386-394.