基于激光全息法的复式光子晶体计算机仿真研究

戚志明, 张 凡

(1. 广东开放大学 广东理工职业学院, 广州 510091;2. 华南理工大学 物理与光电学院, 广州 510641)

0 引 言

随着光子学、半导体物理学及微加工技术的发展,人工微结构的研究蓬勃发展,光子晶体是其中最重要的一类微结构,其潜在的基础研究价值和广阔的应用前景引起了人们的广泛关注。光子晶体是由介电材料周期排列而成的人工微结构[1-3],是一种能在亚波长尺寸上控制光子行为的特殊人工结构,具有类似于半导体的能带结构,可在亚波长尺度上控制光子运动,被认为是最有可能替代硅半导体的新型材料,被喻为光子学中的半导体。

光子晶体具有许多独特的物理性质,例如光子禁带、光子局域[2-5]。其中光子禁带是由布里渊区边界的多重散射产生的特殊频率范围,落在该频率范围内的电磁波在光子晶体内部沿任何方向均无法传播,人们利用光子禁带制作了宽带全角介质反射镜、光子晶体发光二极管、光子晶体天线等[6-9];光子局域是在完整光子晶体中引入缺陷打破对称性产生的,它位于光子禁带中,具有很高的态密度[10-12],人们提出了光子晶体微腔、光子晶体波导等应用[13-15]。除了光子禁带和光子局域,人们发现光子晶体通带存在的奇特色散特性能够产生多种有趣的反常折射效应[16-20],包括负折射[21-25]、自准直[26-29]和超棱镜效应[30-31]。其中负折射指的是入射光和折射光位于法线同一侧的现象,通常产生于负色散能带[32],其群速度跟波矢方向相反;自准直效应的主要特点是光在界面上的折射方向几乎不受入射角度的影响,而且在光子晶体内部传播时几乎不发生衍射,故又称无衍射光传播,它一般产生于光子能带面的平坦区域;超棱镜效应是指折射光的角度对波长或者入射角度变化极端敏感的现象,其分光的灵敏程度可比传统棱镜高100到1 000倍,而体积只有常规棱镜的百分之一大小[30],超棱镜效应一般产生于光子能带第一布里渊区边角附近,相应的等频线表现出极端的各向异性,从而使得光子晶体内部的折射角对波长或入射角度的变化极其敏感。这些反常折射效应在众多领域有着十分重要的应用,例如用于设计光分束器、光开关、光波导等器件[31,33-34]。

随着对光子晶体研究的进一步深入,人们提出了复式晶格光子晶体的概念。通过类比晶格结构的分类,光子晶体可分为简单晶格光子晶体和复式晶格光子晶体(后文简称为简单光子晶体和复式光子晶体),其中前者由单个晶格组成,后者则由2套或以上简单光子晶体相互嵌套而成。相比简单光子晶体,复式光子晶体具有更丰富的物理特性,例如,它具有更低的结构对称性,可以解除光子能带简并造成的对光子带隙宽度的限制,增大完全光子禁带范围,例如通过选择合适的参数和占空比可在二维复式正方晶格光子晶体中实现类似三维光子晶体的完全光子禁带[35]。此外复式光子晶体具有多套可灵活设计的几何参数和材料参数,具有更多的设计和调控自由度,这为人们进一步研究光子晶体更多的新颖物理性质和潜在应用提供了更广阔的舞台。

在光子晶体制备方面,人们提出了多种制作方法,主要包括精密机械加工技术[36]、半导体微加工技术[37]、逐层叠加方法[38-39]、激光直写法[40]、胶体自组装[41]和激光全息法[42-44]等。精密机械加工技术主要应用于制作晶格周期常数在厘米至毫米量级的微波波段光子晶体,对于更小晶格常数的光子晶体无能为力;半导体微加工技术是基于半导体成熟工业技术发展起来的,是一种制备近红外、可见光波段光子晶体的可靠方法,但是该方法工艺复杂,造价比较昂贵;逐层叠加法是利用半导体硅处理技术将许多层二维周期结构按一定规律叠加构成三维光子晶体,这种方法虽然可得到高质量的拥有完全带隙的光子晶体,然而其制造工艺繁琐,造价相当昂贵;胶体自组织法生长的颗粒一般为球形,适用于制作面心立方或体心立方等三维光子晶体,但其占空比控制困难;激光直写法利用光敏材料的双光子聚合反应,由聚焦的飞秒激光逐点刻写微结构,其效率较低,聚合的单元一般为椭球。与上述方法不同,激光全息法利用多束相干激光干涉产生光强有序分布的周期全息图样,并记录于合适材料上得到所需微结构,是一种适用于制作各种维度光子晶体的极具潜力的微加工技术,它具有大面积、制作成本低、高效灵活、干涉图样丰富等独特的优势,已被用于制作二、三维周期结构和准晶结构等各类微结构[42-46],而且还可结合实际需要进行多次曝光制作缺陷等。尤其值得指出的是,激光全息法中参与干涉的光束数量可根据需要灵活选取,通过调整干涉光束构型等参数获得不同维度、不同类型的复杂图样或复式微结构,这使得激光全息法在制作复式光子晶体方面具有独特的优势。

本文从多光束干涉原理出发,从理论上研究多光束干涉产生复式光子晶体的实现机理及光束配置,利用计算机编程模拟多光束干涉,系统研究单束、两束和三束光的偏振度变化对光子晶体元胞形状及对比度的影响,发现可产生圆环、缺口环、弯月形、矩形等多种不同元胞形状的复式光子晶体。这些研究表明激光干涉法在设计特殊元胞形状的复式光子晶体中具有独特的优势,对复杂光学微结构的实验制备具有指导意义。

1 多光束全息干涉法及复式光子晶体形成机理

1.1 全息干涉法原理

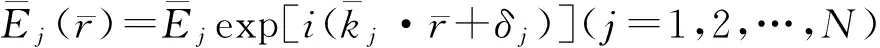
(1)

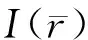
1.2 复式光子晶体形成机理及计算机仿真

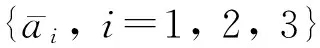
结合上述分析和式(2)可看出,当非共面光束超过3束(N>3)时,将有3个或以上独立的波矢差,一般而言将产生三维的光子晶体,然而在特殊配置情况下,也可出现二维的复式光子晶体。下面以6束光产生二维复式三角光子晶体为例,系统研究复式光子晶体实现机理及光束偏振组合的影响规律。

(a)—光束配置; (b)—偏振分解示意图(以为例); (c)—光束配置投影图及图1 复式三角光子晶体光束配置及示意图Fig.1 Beam configuration for triangular CPC and schematic sketch of

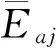
干涉结果清晰程度是全息干涉效果的重要指标,采用干涉对比度进行描述:

(3)

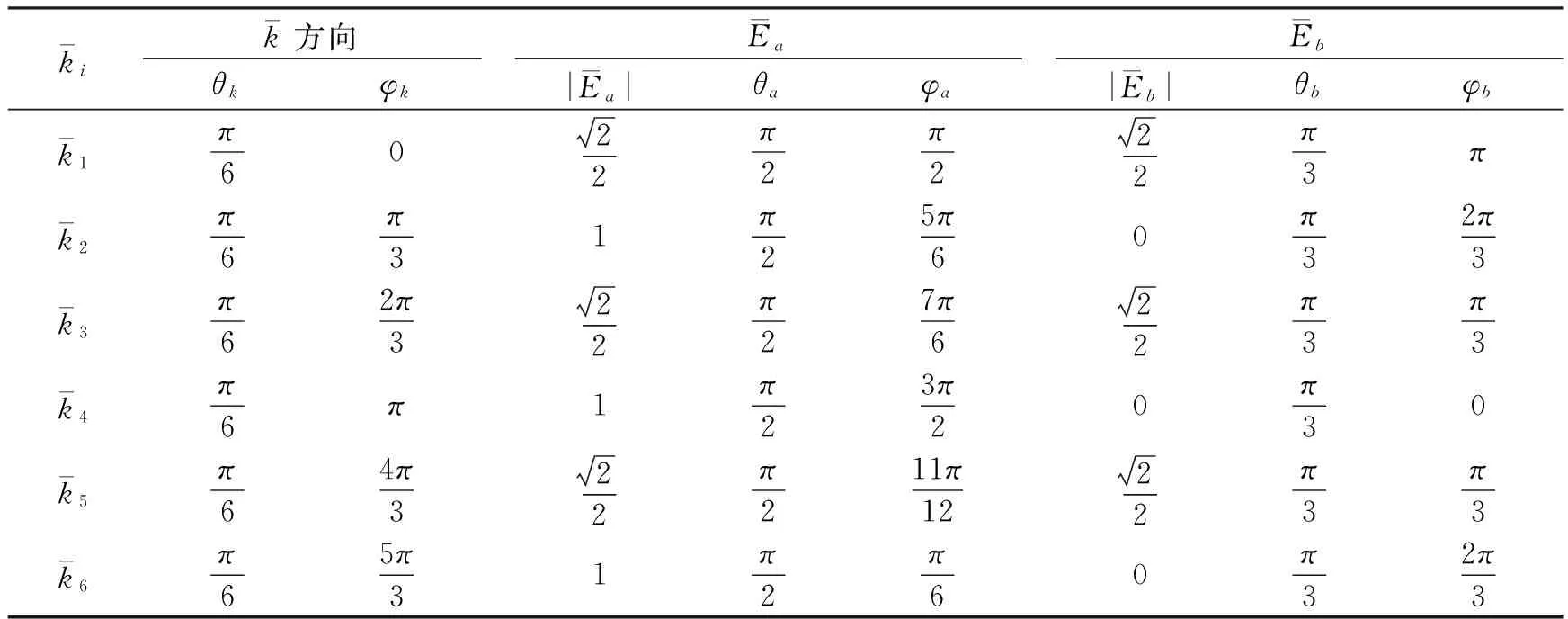
其中,Imax、Imin分别为干涉光强的最大、最小值。当Imin=0时,V=1,干涉条纹最清晰,此时称为完全相干;当Imax=Imin,光强呈全明或全暗,无干涉条纹,此时称为完全不相干;当0

(a)—阈值为3; (b)—阈值为7。图2 复式三角光子晶体仿真实例Fig.2 Simulation examples of triangular CPC

kik方向θkφkEa|Ea|θaφaEb|Eb|θbφbk1π6022π2π222π3πk2π6π31π25π60π32π3k3π62π322π27π622π3π3k4π6π1π23π20π30k5π64π322π211π1222π3π3k6π65π31π2π60π32π3

2 偏振组合对复式光子晶体元胞的影响研究

由公式(2)分析可知,光子晶体的产生与参与干涉光束的偏振密切相关,各光束的偏振度以及偏振组合方式均对其元胞形状和对比度有显著影响。由于光束偏振可为线偏振、椭圆偏振、圆偏振等不同的形式,再考虑到椭圆偏振光的不同偏振度,干涉光束的偏振组合种类十分繁多,难以一一分析。为简便起见,本文重点探讨单束偏振变化、2束或3束干涉光的偏振度同时变化(保持其他各光束的偏振度为0)3种情况下,光束偏振组合对光子晶体元胞形状和对比度的影响。其他更复杂的偏振组合情况,例如各束光的偏振同时变化[具体演变过程为线偏振→椭圆偏振→圆偏振→椭圆偏振(主轴旋转90°)→线偏振(旋转90°)],可按类似方法进行研究,在此不予赘述。

2.1 单束光偏振度变化影响

γ1=0,V=0.9998γ1=0.5,V=0.9920γ1=1.0,V=0.9751γ1=106,V=0.9250

图3单个偏振(γ1)变化的仿真结果
Fig.3 Simulations for variation ofγ1

2.2 2束光偏振度同时变化影响

下面讨论2束光的偏振度同时变化对光子晶体微结构的影响。同样从最简单的偏振组合情况出发,即γj=0 (j=1,2,…,6),由于光束配置的对称性,经过分析发现所有可能的组合可简化归纳为邻(γ1、γ2)、间(γ1、γ3)、对(γ1、γ4)3种情况(其他各光束的偏振度保持为0)。

γ1=γ2=0,V=0.9998γ1=γ2=1.0,V=0.9661γ1=γ2=2.0,V=0.9633γ1=γ2=106,V=0.9588

图4 “邻”情况:(γ1、γ2)同时变化的仿真结果Fig.4 Simulations for adjacent case (γ1, γ2)

图5 “间”情况:(γ1、γ3)同时变化的仿真结果Fig.5 Simulations for separated case (γ1, γ3)

图6 “对”情况:(γ1、γ4)同时变化的仿真结果
Fig.6 Simulations for opposite case (γ1,γ4)

2.3 3束光偏振度同时变化情况

下面讨论3束光偏振度同时变化的影响。同样从最简单的偏振组合即γj=0 (j=1,2,…,6)出发,由于光束配置的对称性,3束光偏振度同时变化的所有可能组合可简化归纳为A(γ1、γ2、γ3)、B(γ1、γ2、γ4)、C(γ1、γ3、γ5)3种情况。

γ1=γ2=γ3=0,V=0.9998γ1=γ2=γ3=1.0,V=0.9761γ1=γ2=γ3=2.0,V=0.9631γ1=γ2=γ3=106,V=0.9424

图7 A(γ1、γ2、γ3)同时变化的仿真结果Fig.7 Simulations for case A(γ1, γ2, γ3)

图8 B(γ1、γ2、γ4)同时变化的仿真结果Fig.8 Simulations for case B(γ1, γ2, γ4)

图9 C(γ1、γ3、γ5)同时变化的仿真结果
Fig.9 Simulations for case C(γ1,γ3,γ5)

3 结 论

本文从理论上研究了激光全息法产生复式光子晶体的实现机理,以6束光干涉产生复式三角光子晶体为例研究了光束配置设计原理。进一步利用计算机仿真技术,系统探讨了单束、2束、3束干涉光的偏振度和偏振组合对元胞形状和对比度的影响。研究表明,通过控制偏振组合可实现圆环、缺口环、弯月状、矩形等各种独特形状的元胞,甚至可获得反结构光子晶体。随着偏振度的增加,对比度主要呈下降趋势(仅3束光的B情况先降后升),但下降幅度各异。以上研究不仅丰富了激光全息法制备光子晶体的内涵,而且为探索复杂、独特元胞的微结构制备提供了行之有效的途经,有助于提高实验效率。

参考文献:

[1]JOANNOPOULOS J D,JOHNSON S G,WINN J N,et al. Photonic grystals: Molding the flow of light[M]. 2nd ed. Princeton: Princeton University Press, 2008.

[2]YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Phys Rev Lett, 1987,58(20):2059-2062.

[3]JOHN S. Strong localization of photons in certain disordered dielectric superlattices[J]. Phys Rev Lett, 1987,58(23):2486-2489.

[4]刘紫雁,唐吉玉,刘娟,等. 介质环型三重晶格光子晶体的带隙[J]. 激光与光电子学进展, 2017,54(11):111603.

[5]陈敏,万婷,王征,等. 宽绝对禁带的一维磁性光子晶体结构[J]. 物理学报, 2017,66(1):014204.

[6]苏安,欧阳志平,王高,等. 二元级联结构光子晶体的全向反射镜功能[J]. 激光与红外工程, 2016,45(S2):S221001.

[7]YIN Y F,LAN W Y,LIN T C,et al. High-speed visible light communication using GaN-based light-emitting diodes with photonic crystals[J]. Journal of Lightwave Technology, 2017,35(2):258-264.

[8]WEILY A R,ESSELLE K P,SANDERS B C. Photonic crystal horn and array antennas[J]. Phys Rev E, 2003,68(1):016603.

[9]FUMEAUX C,FUJITA M,YAMADA R,et al. All-dielectric integration of dielectric resonator antenna and photonic crystal waveguide[J]. Optics Express, 2017,25(13):14706-14714.

[10]FIGOTIN A,GORENTSVEIG V. Localized electromagnetic waves in a layered periodic dielectric medium with a defect[J]. Phys Rev B, 1998,58(1):180-188.

[11]XIAO X,WANG W,LI S,et al. Investigation of defect modes with Al2O3and TiO2in one-dimensional photonic crystals[J]. Optik-International Journal for Light and Electron Optics, 2016,127(1):135-138.

[12]宗易昕,夏建白,武海斌. 介质/介质和金属/介质光子晶体的光子能带和光子态密度[J]. 激光与光电子学进展, 2016,53(3):031602.

[13]钱琛江,谢昕,杨静南,等. 二维平板光子晶体微腔与波导的耦合[J]. 激光与光电子学进展, 2017(3):1-13.

[14]TONG W,WANG J,WANG J,et al. Magnetically tunable unidirectional waveguide based on magnetic photonic crystals[J]. Applied Physics Letters, 2016,109(5):053502.

[15]TERADA Y,MIYASAKA K,KONDO K,et al. Optimized optical coupling to silica-clad photonic crystal waveguides[J]. Optics Letters, 2017,42(22):4695-4698.

[16]GRALAK B,ENOCH S,TAYEB G. Anomalous refractive properties of photonic crystals[J]. J Opt Soc Am A, 2000,17(6):1012-1020.

[17]BRAVO-ABAD J,OCHIAI T, SNCHEZ-DEHESA J. Anomalous refractive properties of a two-dimensional photonic band-gap prism[J]. Phys Rev B, 2003,67(11):115116.

[18]FOTEINOPOULOU S,SOUKOULIS C M. Electromagnetic wave propagation in two-dimensional photonic crystals: A study of anomalous refractive effects[J]. Phys Rev B, 2005,72(16):165112.

[19]LI Z. Anomalous transport of light in photonic crystal[J]. Science China(Information Sciences), 2013,56(12):120405.

[20]STALIUNAS K,MAIGYTE L,BOTEY M,et al. Beam shaping in two-dimensional metallic photonic crystals[J]. Journal of the Optical Society of America B, 2014,31(4):686-690.

[21]OHLINGER K,OLVERA I,LIN Y K. Negative refraction behaviors in two-dimensional elliptical-rod photonic crystals in a centered rectangular lattice[J]. J Appl Phys, 2009,106(2):023516.

[22]UMMER K V,VIJAYA R. All-angle negative refraction effects and subwavelength imaging in photonic crystals with honeycomb lattice[J]. Journal of Nanophotonics, 2017,11(3):036005.

[23]ROMANO S,DE LUCA A C,DE TOMMASI E,et al. Observation of resonant states in negative refractive photonic crystals[J]. Journal of the European Optical Society, 2014,9(1):14006.

[24]UMMER K V,VIJAYA R. All-angle negative refraction effects and subwavelength imaging in photonic crystals with honeycomb lattice[J]. Journal of Nanophotonics, 2017,11(3):036005.

[25]MENG F,LI S,LIN H,et al. Topology optimization of photonic structures for all-angle negative refraction[J]. Finite Elements in Analysis & Design, 2016(S117/118):46-56.

[26]KOSAKA H,KAWASHIMA T,TOMITA A,et al. Self-collimating phenomena in photonic crystals[J]. Appl Phys Lett, 1999,74(9):1212-1214.

[27]WITZENS J,SCHERER A. Efficient excitation of self-collimated beams and single Bloch modes in planar photonic crystals[J]. J Opt Soc Am A, 2003,20(5):935-940.

[28]LEE S G,JUNG S Y,LEE J,et al. Self-collimation-based photonic crystal Mach-Zehnder demultiplexer[J]. Journal of Physics D Applied Physics, 2016,18(9):095103.

[29]ZUO Y F,LI P L,LUAN K Z,et al. Heterojunction polarization beam splitter based on self-collimation in photonic crystal[J]. Acta Physica Sinica, 2018,67(3):034204.

[30]KOSAKA H,KAWASHIMA T,TOMITA A,et al. Superprism phenomena in photonic Crystals[J]. Phys Rev B, 1998,58(16):10096-10099.

[31]LIANG W,LIU X,YIN M. Large-angle beam splitter with sensitive adjustable power ratio based on superprism effect[J]. Journal of Physics D-Applied Physics, 2013,46(49):495109.

[32]NOTOMI M. Theory of light propagation in strongly modulated photonic crystals: Refractionlike behavior in the vicinity of the photonic band gap[J]. Phys Rev B, 2000,62(16):10696-10705.

[33]崔珂珂,李培丽,郑加金. 基于光子晶体自准直效应的太赫兹波开关[J]. 光电子·激光, 2017,28(8):824-829.

[34]任坤,范景洋,任晓斌. 非互易光传输方向的主动调控[J]. 光学学报, 2017,37(7):0726003.

[35]冯志芳,王义全,张道中,等. 利用复式原胞实现二维光子晶体中的完全带隙[J]. 北京工业大学学报, 2004,30(3):390-392.

[36]YABLONOVITCH E,Gmitter T J,Leung K M. Photonic band structure: the fcc case employing non-spherical atoms[J]. Physical Review Letters, 1991,67(17):2295-2298.

[37]LONCAR M,DOLL T,VUCKOVIC J,et al. Design and fabrication of silicon photonic crystal optical waveguides[J]. Journal of Lightwave Technology, 2000,18(10):1402-1411.

[37]NODA S,YAMAMOTO N,IMADA M,et al. Alignment and stacking of semiconductor photonic bandgaps by wafer-fusion[J]. Lightwave Technology Journal of, 1999,17(11):1948-1955.

[38]ÖZBAY E,ABEYTA A,TUTTLE G,et al. Measurement of a three-dimensional photonic band gap in a crystal structure made of dielectric rods[J]. Phys Rev B, 1994,50(3):1945-1948.

[40]JIA T,BABA M,SUZUKI M,et al. Fabrication of two-dimensional periodic nanostructures by two-beam interference of femtosecond pulses[J]. Optics Express, 2008,16(3):1874-1878.

[41]JIN C J,MCLACHLAN M A,MCCOMB D W,et al. Template-assisted growth of nominally cubic (100)-oriented three-dimensional crack-free photonic crystals[J]. Nano Letters, 2005,5(12):2646-2650.

[42]MAO W D,ZHONG Y C,DONG J W,et al. Crystallography of two-dimensional photonic lattices formed by holography of three noncoplanar beams[J]. Journal of the Optical Society of America B: Optical Physics, 2005,22(5):1085-1091.

[43]LU H,ZHAO Q L,ZHANG Q Y,et al. Fabrication of two-dimensional superposed microstructure by interference lithography[J]. Appl Opt, 2012,51(3):302-305.

[44]吕浩,尤凯,兰燕燕,等. 非对称光束干涉制备二维微纳光子结构研究[J]. 物理学报, 2017,66(21):217801.

[45]SUN X H,WU Y L,LIU W,et al. Fabrication of ten-fold photonic quasicrystalline structures[J]. AIP Advances, 2015,5(5):057108.

[46]王霞,吕浩,赵秋玲,等. 激光全息光刻技术在微纳光子结构制备中的应用进展[J]. 光谱学与光谱分析, 2016,36(11):3461-3469.