Gas emission source term estimation with 1-step nonlinear partial swarm optimization-Tikhonov regularization hybrid method☆

Denglong Ma *,Wei Tan Zaoxiao Zhang ,Jun Hu

1 School of Food Equipment Engineering and Science,Xi'an Jiaotong University,Xi'an 710049,China

2 State Key Laboratory of Multiphase Flow in Power Engineering,Xi'an Jiaotong University,Xi'an 710049,China

3 School of Chemical Engineering and Technology,Xi'an Jiaotong University,Xi'an 710049,China

4 School of Chemical Engineering,Northwest University,Xi'an 710069,China

1.Introduction

Gas emission may lead to potential safety risk,thus source estimation for emission event is vital to the safety management and risk treatment[1,2].For example,CO2gases stored in geological reservoir may flee from the site and leak into atmosphere[2].In this case,identifying the source parameters such as source strength and location is important to estimate the leakage source.Researchers have done many work about source term identification with different inverse problem solution methods.Corresponding to the forward gas dispersion process,the source estimation is an inverse problem,as shown in Fig.1.For forward dispersion,the concentration distribution is predicted with the information of source term,atmosphere and terrain condition.But in the inverse problem,the source terms like emission rate and location are required to be determined when the concentrations of leakage gases are known as well as atmosphere and terrain condition.

Fig.1.Illustration of inverse gas emission process.

To solve this problem,many methods have been proposed.Because inverse dispersion problem is ill-posed,the ill-conditional results are often obtained by solving the inverse dispersion equations directly.For instance,the solution results from inverse dispersion equations depend on the boundary condition and initial parameters greatly and output error may be caused by slight input variation.Therefore,different optimization methods were utilized to estimate the gas leakage source parameters and some parameters in other inverse problem[3-5].Cantelli[6],Chen[7],and Luo et al.[8]used optimization methods to reconstruct the source term under different cases.Ma et al.compared different optimization methods including simplex,pattern search,genetic algorithm(GA)and their hybrid algorithms to identify source parameters[9,10].Although optimization methods can deal with ill posed problem and estimate multiple parameters simultaneously,there are still some problems in error treatment and uncertainty analysis.Stochastic probability methods seem to be the better method with probability results,which are more acceptable than single estimate values with optimization methods to solve inverse problem.Zhao et al.proposed differential evolution and probability hybrid method to estimate kinetic parameters for biochemical systems[11].Cang et al.used Kalman filtering method to estimate catalytic activity using an unscented in condensation reaction[12].Hazarta[13],Kopka[14],Guo[15]and Zhang et al.[16]combined Bayesian inference and Markov Chain Monte Carlo(MCMC)method to estimate the gas emission parameters for point source,mobile source and indoor source.Flesch et al.proposed a computation process for forward and backward gas dispersion simulation in atmosphere under different space dimensions based on Lagraagian stochastic(LS)model[17].But both MCMC and LS method have the problem in low computation efficiency,especially for large computation space,as discussed by Ma et al.[18].Minimum relative entropy(MRE)method is also a probability method based on Bayesian interface.Neupauer et al.applied MRE method to solve linear inverse problem[19].Ma et al.coupled MRE method with particle swarm optimization(PSO)algorithm to estimate gas emission source[20].Their results showed that MRE-PSO method improved the computation efficiency greatly.However,MRE method depends on the prior information such as prior error,lower and upper boundary,which is always difficult to be known in the real case.Hence,it is necessary to find a source term identification method with high computation efficiency and probability estimation results but without needing prior error information.

Parameter regularization method has been used to solve many inverse problems,especially for linear inverse problem[21-26].This method is based on the least squares solution,and it introduces a regularization operator and a regularization parameter to solve the ill-posed inverse problem.If the regularization parameter is found by the method like L-curve or GCV(Generalized Cross Validation),the prior noise information is not be required.Further,the confidence interval at different probability levels can be calculated with stochastic method in regularization method.Therefore,it is possible to use regularization method without prior error information to identify the source parameters with confidence intervals.Different regularization methods have been designed to solve inverse problem based on different regularization terms[21,22].Tikhonov regularization is one of the most widely-used methods,which is often applied for solving ill-posed inverse problem.Bozzoli et al.[23]estimated the local heat-transfer coefficient in laminar flow regime in coiled tubes by Tikhonov regularization method[23].Wei et al.employed Tikhonov regularization method to estimate the parameters of solute transport soil process[24].Yuan et al.used Tikhonov regularization method to identify the partial blockage parameters in natural gas pipeline under the case with random errors[25].For gas emission term identification problem,Kathirgamanathan proposed a computation process for contaminant gas emission rate estimation with Tikhonov regularization method[26].In order to estimate multiple source parameters,he further presented a nonlinear regularization process.But different parameters were estimated separately with repeated optimization process[26].Ma et al.transformed the nonlinear gas dispersion model to be a linear form and modified Tikhonov regularization equation,and then they proposed a linear regularization method coupled Tikhonov regularization and PSO algorithm to identify the emission rate,source location simultaneously[18].They also designed 2-step nonlinear PSO-Tikhonov regularization computation process according to Kathirgamanathan's idea.The results showed that linear PSO-Tikhonov method estimated multiple source parameters successfully and the computation efficiency was improved greatly compared with 2-step nonlinear PSO-Tikhonov method.However,the linear assumption in linear PSO-Tikhonov regularization method may bring some errors into estimation and the confidence intervals obtained by both linear and 2-step nonlinear PSO-Tikhonov method seem too wide.Therefore,a new nonlinear regularization method will be designed with nonlinear forward model to estimate multiple gas emission source parameters simultaneously.

2.Principle

Tikhonov regularization is based on the least square principle.But it is different from common least square method by introducing regularization operator and parameters.Tikhonov regularization method is often utilized to solve the linear inverse problem.The basic expression of the regularization form is shown with Eq.(1),

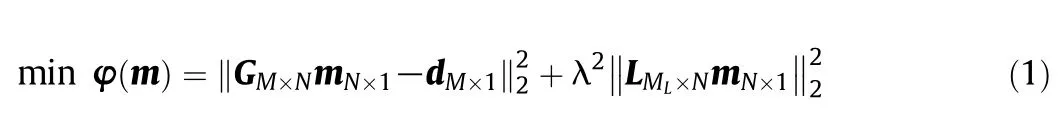
where G is the transfer matrix of linear problem Gm=d with the size of M by N;m is the parameter matrix sized with N by 1;d is the measurement data with the length of M;λ is the regularization parameter,L is a regularization matrix and ‖⋅‖ denotes the Euclidian norm.MLis the length of the row of matrix L.

The first term in Eq.(1)represents the errors from the model and data while the second term is that from the regularization process.The regularization parameter λ balances the errors between two terms.L is a sparse matrix,which are used to differentiate m for the purpose of regularization.‖Lm‖is a finite-difference approximation that is proportional to the first derivative of m.Here,the method presented by Aster et al.[27]was adopted to approximate the derivative of m.In this method,the problem can be discretized by simple collocation.When the regularization matrix is determined with certain method,the regularization parameter will dominate the estimation results.The selection of optimal regularization parameter is based on minimizing the total error.The regularization error approaches zero as λ → 0,while the error due to noise in the data increases as λ → 0.Discrepancy principle is a well-known method to determine the regularization parameter,but it relies on prior information on the noise level.On the other hand,methods such as generalized cross validation(GCV),L-curve and quasi-optimality criterion do not require any information about the noise level.Here,L-curve method was used to choose the regularization parameter,which was introduced by Hansen[28].

The L-curve is simply a logarithmic plot of residual norm ‖Gm-d‖22versus the solution norm ‖Lm‖22for a set of admissible regularization parameter.In this way,the L-curve displays the compromise between the minimization of these two terms.The ‘corner’of the L-curve is defined as the point on the L-curve

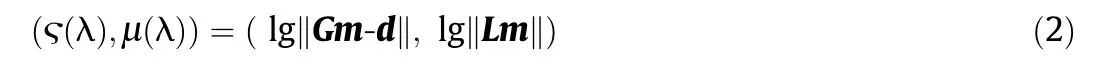
with the maximum curvature.Here the curvature k is given by

where the differentiation is with respect to λ.

With every element in the regularization set,the damped least squares problem like Eq.(1)is solved.If the problem has a linear form and satis fies the structure of common Tikhonov method,singular value decomposition(SVD)can be used to solve Eq.(1).But gas dispersion process is a classical nonlinear problem,if multiple source parameters are required to be determined,SVD is failure in this case.Particle swarm optimization(PSO)is a good method to solve the optimization problem and thus it can be used to obtain the optimal estimation m under certain regularization parameter.

Because Eq.(1)is not proper to estimate multiple gas emission source parameters,Ma etal.[18]proposed linear PSO-Tikhonov method,as shown with Eq.(5),after transforming the nonlinear Gaussian dispersion model to be a linear form and modi fied Eq.(1)to be

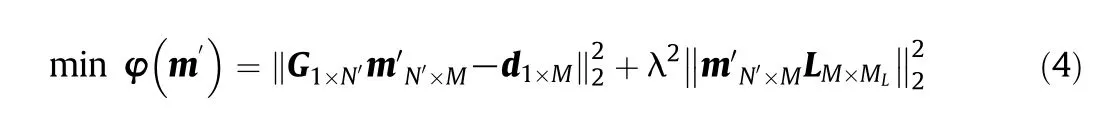
where m′is the transformed parameter matrix and N′is the length of m′.In this case m’can be estimated successfully with linear PSO-Tikhonov method and then the original estimation parameters can be obtained.

Additionally,according to the presentation of Kathirgamanathan[26],the gas emission source parameters can be determined with two steps nonlinear method to solve the problem as Eq.(5).

where m0is the matrix only including location parameters and m1is the source strength parameter.The transfer matrix G(m0)is a nonlinear function about location parameters and the source strength is linear to the concentration d.The source location parameters are determined if rst with an unit emission rate by optimization method.Then,the emission rate is calculated with the estimated location parameters in the previous step.The detail of linear PSO-Tikhonov and 2-step nonlinear method computation process were discussed in the paper of Ma et al.[18].

Although linear PSO-Tikhonov method cost much less time than 2-step nonlinear method as discussed in Ma et al.[18],there are still some problems due to the assumption of linear transformation.Hence,1-step nonlinear PSOTikhonov method is designed to estimate multiple emission source parameters.Gaussian dispersion model is accepted as the forward dispersion model[29],as shown with Eq.(6)

where C(x,y,z)is the concentration of the emission gas(g·m-3)at the downwind distance xm away from the source,ymlaterally from the centerline of the plume,and z m above ground level.Qcis the emission rate of the source(g·s-1).u is the wind speed(m·s-1).h is the effective height of the source above ground level(m).σyand σzare the standard deviations of a statistically normal plume in lateral and vertical dimensions,respectively.

The source parameters including emission rate,downwind and crosswind distance to the certain sensor are required to be estimated when the emission gas concentrations at different sensors have been measured.In this case,the regularization equation becomes

where the first term is a nonlinear form including all source parameters.The computation process of 1-step nonlinear PSO-Tikhonov regularization method is illustrated in Fig.2.

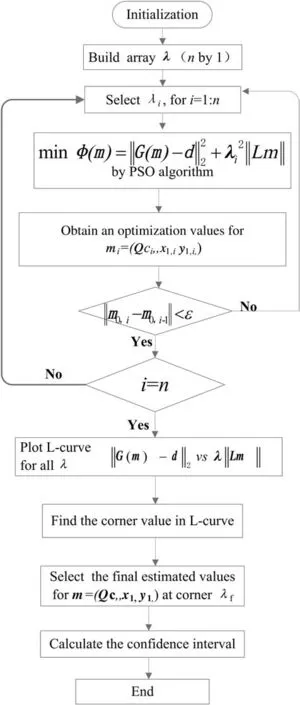
Fig.2.Computation flow of 1-step nonlinear PSO-Tikhonov nonlinear method for source identification.

First,an array with different regularization values is set.For every regularization parameter,the best estimation for source parameters will be obtained with PSO algorithm by the cost function of Eq.(7).It is noted from Fig.2 that 1-step nonlinear method proposed here only needs one PSO computation process with a certain regularization parameter.It will improve the computation efficiency compared with 2-step nonlinear PSO-Tikhonov method in the paper of Ma et al.[18].The curve of‖Gm-d‖22vs.‖Lm‖22under all regularization values is then plotted and the point with the maximum curvature is selected as the best estimation parameters.Finally,the confidence interval under certain probability level is calculated.The difference between 1-step nonlinear and linear PSO-Tikhonov method lies in the regularization term.Hence,the confidence intervals will be calculated with different method compared with linear inverse model.For nonlinear method,the confidence intervals can be determined with Eq.(8)[26,27].

which is based on t-distribution.α is the probability level and f is the degree of freedom.Smiis the square roots of the diagonal elements of variance-covariance matrix S2(WTW)-1.S is given by

Here,n is the length of data,r is the length of parameter vector.m=[Qc,x1,y1]and W is a matrix of the partial derivatives of G,which is obtained by W=[G J],where J is n×2 matrix,

The variance-covariance matrix of estimated parameter^m is

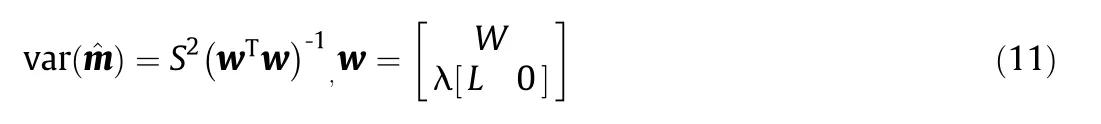
3.Case Study

It was noticed from the research of Ma et al.[18]that the emission rate can be easily determined by common Tikhonov regularization with SVD solution method when the location is known.But if both the emission rate and location are required to be determined,SVD is valid.Therefore,the method proposed in this paper is designed to estimate source strength and location parameters simultaneously.The method will be tested with both simulation and experiment cases.

3.1.Simulation case

First,a simulation scenario is built to test the performance of source parameter estimation method.Here,the leakage source is set with the emission rate of 32 g·s-1and the source stack height of 0.006 m.The measurement height z=1 m and the wind speed at 1 m above ground u=6.7 m·s-1.The gases emitfrom the near surface and the roughness height of the ground z0is assumed as 0 m.The atmosphere is under Pasquill stability class “E”.The downwind distance of measurement sensor is 30,50,70,100 and 150 m away from the emission source and the crosswind distance is from 5 to 20 m with 5 m interval.Gaussian dispersion model is used to predict the concentrations at the sensors.A randomnoise with mean intensity of0.01 times of measure mentresults are added on the simulation results.The original point in sensor coordinate system locates at the position with the downwind distance from the source of 30 m and the crosswind distance of 5 m.The emission rate,downwind and crosswind distance of the original sensor are the estimate parameters.

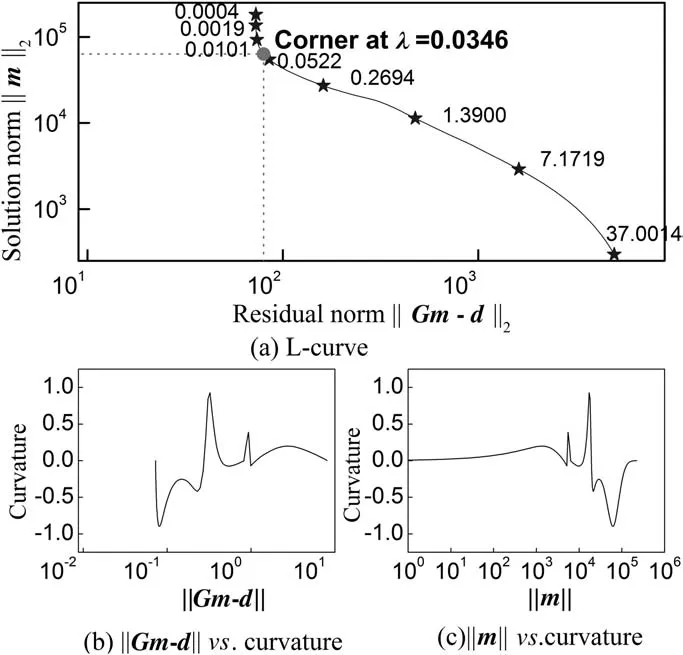
Fig.3.L-curve for simulation case with 1-step nonlinear PSO-Tikhonov method.

Table 1 Results of source strength and location estimation by 1-step nonlinear PSO-Tikhonov method

Based on the computation process of Fig.2,the L-curve of‖Gm-d‖22vs.‖Lm‖22with different values of λ is shown in Fig.3.Here,L is one order regularization matrix.

Itis shown fromthe L-curve in Fig.3 thatthere is an obvious corner on the curve and the optimal regularization parameterin this case is 0.0346,where the curvature has the maximum value.The estimate results of source term at 95%probability level are listed in Table 1.The source term includesemission rate Qc,downwind distance x0and crosswind distance y0.The realvalue of estimate parameter m=[Qc,x0,y0]=[32,30,5].Itis seen from the results that the estimated valuesundersimulation case is very close to the real value.In order to evaluate the performance of the estimation method,the skillscore proposed by Ma etal.[9]was accepted.Sq,Sxand Syare the skill scores for emission rate,downwind and crosswind distance,respectively.The less skill score,the better estimation performance of the method.It is noted from Table 1 that the skill scores of 1-step nonlinear PSO-Tikhonov regularization method to identify the source parameters are all less than 0.1,which proves the feasibility of this method to estimate the source term.

3.2.Experiment case

Prairie Grass emission experiment is a classic gas emission experiment,where SO2gases was controlled to release with differentemission rates under different atmosphere conditions in open air[30].68 release experiments were sampled with sensor array.Here,two releases under different atmosphere conditions were selected to verify the method proposed in this paper,where release 17 was under stable atmospheric stability condition while release 33 was under unstable condition.

The L-curve during the test process of release 17 with 1-step nonlinear PSO-Tikhonov regularization method is illustrated in Fig.4.The optimal regularization parameter in this case is 67.03.The results are listed in Table 1 too.The real value of source term in this experiment case is m=[Qc,x0,y0]=[56.5,47.55,15.45].The skill scores of the method to estimate source term in this case are larger than that in simulation case due to the data and model errors.But all skill scores are less than 0.5,especially the skill scores of location parameter.

Further,the experiment case of release 33 was tested with 1-step nonlinear PSO-Tikhonov method.The L-curve in this process is shown in Fig.5.The optimal regularization parameter in this case is 0.6870,which is less than that in the case of release 17.It is also noted that the optimal regularization parameter in experiment case is larger than that in simulation case,which may result from the errors in data and forward model.The results based on release 33 case are also listed in Table 1.The real value of source term in this experiment case is m=[Qc,x0,y0]=[94.7,49.62,6.09].The results in Table 1 indicate that the skill score of the method in this case is also less than 0.5.Therefore,it is feasible to identify the source parameters by 1-step nonlinear PSOTikhonov method proposed in this paper.

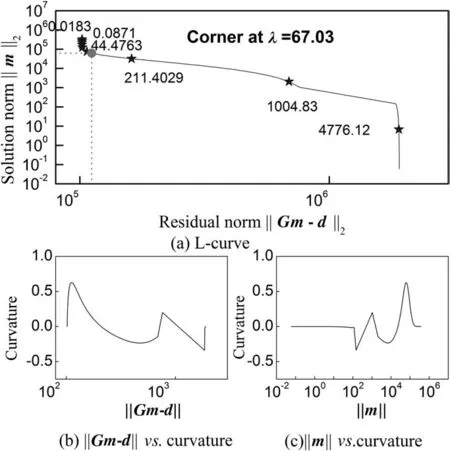
Fig.4.L-curve for Release 17 experiment with 1-step nonlinear PSO-Tikhonov method.

Fig.5.L-curve for Release 33 experiment with 1step PSO-Tikhonov nonlinear method.

4.Discussion

In order to compare the performances of linear,nonlinear1-step and 2-step PSO-Tikhonov regularization method,the cases were tested with the same computer condition using Matlab software.The comparison results of computation time are illustrated in Fig.6.It is noted that the computation time with 1-step nonlinear PSO-Tikhonov method is about half of that with 2-step nonlinear method.Although linear PSOTikhonov method has the highest computation efficiency,its confidence interval seems too large as discussed in the paper of Ma et al.[18].The estimated results by 2-step nonlinear and linear PSO-Tikhonov method are summarized in Table 2.Compared with the results in Table 1,it is noticed that the confidence interval calculated by 1-step nonlinear method is more narrower than that by linear and 2-step nonlinear PSO-Tikhonov method and it seems more reasonable.

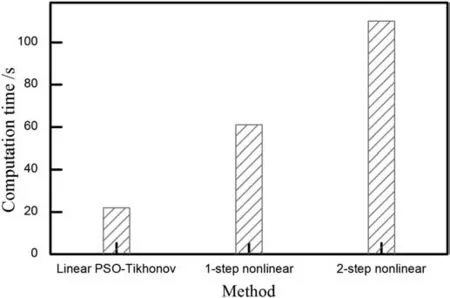
Fig.6.Comparison of computational time with different PSO-Tikhonov source identification methods.

Table 2 Results of source term parameters by 2-step nonlinear and linear PSO-Tikhonov regularization method with experiment case[18]

Fig.7 shows the skill scores for different source parameters with different regularization methods.It is seen that the skill scores of different regularization methods are close to each other.But 1-step nonlinear PSO-Tikhonov regularization method has a better total performance in the case of simulation and release 33 experiment,especially for the parameter estimation of source strength and downwind distance.Therefore,the method proposed in this paper has some advantages in both confidence interval and estimation results.

Fig.7.Comparison of estimation results with different PSO-Tikhonov regularization methods.

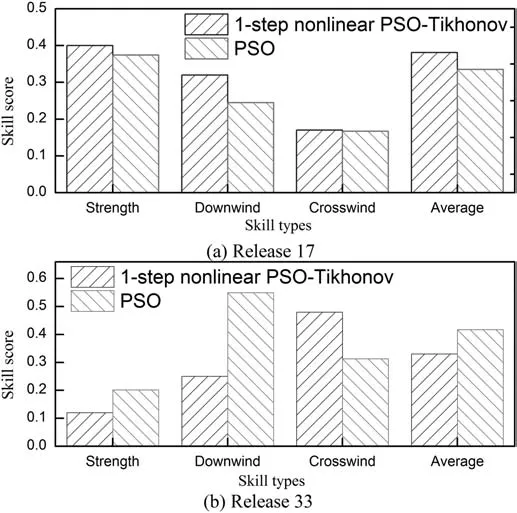
Fig.8.Comparison of skill scores with 1-step nonlinear PSO-Tikhonov and single PSO algorithm.

Single PSO algorithm was also used to test the source parameter estimation,which is compared with 1-step nonlinear PSO-Tikhonov regularization method,as shown with Fig.8.It is noted that the skill scores of 1-step nonlinear PSO-Tikhonov method are similar to that of single PSO method under the case of release 17.But the performance of the method proposed in this paper is better than that of single PSO in the case ofrelease 33.A more important property of 1-step nonlinear PSO-Tikhonov method than that of single PSO is reasonable confidence interval.Hence,1-step nonlinear PSO-Tikhonov regularization method is a potentially better method to estimate source parameters compared with the single PSO method.

5.Conclusions

Since previously proposed 2-step nonlinear and linear PSOTikhonov regularization method have some problems in computation time and confidence interval,a new 1-step nonlinear hybrid method coupled with Tikhonov regularization and PSOalgorithmwas presented in this paper,which was also tested with simulation and experiment cases.

The test results showed that 1-step nonlinear PSO-Tikhonov regularization method is feasible to estimate multiple emission source parameters with reasonable confidence intervals at certain probability level.

The computation time of1-step nonlinear PSO-Tikhonov regularization method is about half of that of 2-step nonlinear method while it is longer than that of linear PSO-Tikhonov method to estimate multiple source parameters.

Although the skill scores of 1-step nonlinear,2-step nonlinear and linear PSO-Tikhonov method to estimate source parameters are close to each other,the skill scores of 1-step nonlinear method are better in some cases than other two methods,especially for source strength and downwind distance estimation.

Compared with 2-step nonlinear and linear PSO-Tikhonov regularization method proposed previously,1-step nonlinear method obtains more reasonable confidence interval at certain probability level.

1-step nonlinear PSO-Tikhonov method discussed in this paper can identify multiple source parameters with the similar skill score with single PSO method.But it performs better in some cases.Moreover,1-step nonlinear PSO-Tikhonov method can provide reasonable confidence interval additionally compared with single PSO method.

Therefore,1-step nonlinear PSO-Tikhonov method proposed in this paper is a potential good method to identify contaminant gas emission source term although it still has some problems.

Nomenclature

C concentration of the emission gas,g·m-3

d measurement data

f degree of freedom

G transfer matrix of inverse problem

h effective height of the source above ground level,m

k curvature of L-curve

L regularization matrix

M length of measurement data

MLlength of the row of regularization matrix

m parameter matrix

N length of parameter matrix

S skill scores for estimate parameter

Smvariance-covariance matrix of regularization form

u wind speed,m·s-1

x downwind distance,m

x0downwind distance of original sensor to the source,m

y crosswind distance,m

y0crosswind distance of original sensor to the source,m

z measurement height above ground level,m

z0roughness height of the ground surface,m

α probability level,100%

λ regularization parameter

σistandard deviations of a statistically normal plume,m

Subscripts

x downwind direction

y crosswind direction

q emission rate

[1]Y.Xu,Z.Y.Wang,Q.X.Zhu,An improved hybrid genetic algorithm for chemical plant layout optimization with novel non-overlapping and toxic gas dispersion constraints,Chin.J.Chem.Eng.21(4)(2013)412-419.

[2]D.L.Ma,J.Q.Deng,Z.X.Zhang,CO2leakage identification in geosequestration based on real time correlation analysis between atmospheric O2and CO2,Chin.J.Chem.Eng.22(6)(2014)634-642.

[3]C.L.Fan,F.R.Sun,L.Yang,A numerical method on inverse determination of heat transfer coefficient based on the rmographic temperature measurement,Chin.J.Chem.Eng.16(6)(2008)901-908.

[4]X.J.Wu,C.Y.Cui,S.Hu,Z.H.Li,C.D.Wu,The velocity measurement of two-phase lf ow based on particle swarm optimization algorithm and nonlinear blind source separation,Chin.J.Chem.Eng.20(2)(2012)346-351.

[5]J.Lang,J.Zhao,Modeling and optimization for oil well production scheduling,Chin.J.Chem.Eng.24(10)(2016)1423-1430.

[6]A.Cantelli,F.D'Orta,A.Cattini,F.Sebastianelli,L.Cedola,Application of genetic algorithm for the simultaneous identification of atmospheric pollution sources,Atmos.Environ.115(2015)36-46.

[7]Z.Q.Chen,Research on Source Identification Approaches for Hazardous Chemical Releases(Ph.D.Thesis)Beijing University of Chemical Technology,Beijing,2013(In Chinese).

[8]P.Luo,The inverse study of the liquefied gas source intensity based on the MATLAB(Master Thesis)Harbin University of Science and Technology,Harbin,2015(In Chinese).

[9]D.L.Ma,J.Q.Deng,Z.X.Zhang,Comparison and improvements of optimization methods for gas emission source identification,Atmos.Environ.81(2013)188-198.

[10]A.J.Lazzús,Prediction of flash point temperature of organic compounds using a hybrid method of group contribution+neural network+particle swarm optimization,Chin.J.Chem.Eng.18(5)(2010)817-823.

[11]C.Zhao,Q.L.Xu,S.M.Lin,X.L.Lin,Hybrid differential evolution for estimation of kinetic parameters for biochemical systems,Chin.J.Chem.Eng.21(2)(2013)155-162.

[12]W.T.Cang,H.Z.Yang,Estimation of catalytic activity using an unscented Kalman filtering in condensation reaction,Chin.J.Chem.Eng.23(12)(2015)1965-1969.

[13]A.Hazarta,J.F.Giovannelli,S.Dubostc,L.Chatellierc,Inverse transport problem of estimating point-like source using a Bayesian parametric method with MCMC,Signal Process.96(Part B)(2014)346-361.

[14]P.Kopka,A.Wawrzynczak,M.Borysiewicz,Application of the approximate Bayesian computation methods in the stochastic estimation of atmospheric contamination parameters for mobile sources,Atmos.Environ.145(2016)201-212.

[15]S.D.Guo,R.Yang,W.G.Weng,Source inversion of toxic gas dispersion in urban areas based on the MCMC method,J.Tsinghua Univ.(Sci.&Technol.)49(5)(2009)11-16(In Chinese).

[16]T.Zhang,H.Zhou,S.Wang,Inverse identification of the release location,temporal rates,and sensor alarming time of an airborne pollutant source,Indoor Air 25(4)(2015)415-427.

[17]T.K.Flesch,J.D.Wilson,L.A.Harper,B.P.Crenna,R.R.Sharpe,Deducing ground-to-air emissions from observed trace gas concentrations:a field trial,J.Appl.Meteorol.44(2005)475-484.

[18]D.L.Ma,W.Tan,Z.X.Zhang,Hu Jun,Parameter identification for continuous point emission source based on Tikhonov regularization method coupled with particle swarm optimization algorithm,J.Hazard.Mater.325(2017)239-250.

[19]R.M.Neupauer,B.Borchers,J.L.Wilson,Comparison of inverse methods for reconstructing the release history of a groundwater contamination source,Water Resour.Res.36(2000)2469-2475.

[20]D.L.Ma,S.M.Wang,Z.X.Zhang,Hybrid algorithm of minimum relative entropyparticle swarm optimization with regularization parameters for gas source term identification,Atmos.Environ.94(2014)637-640.

[21]R.M.Neupauer,A Comparison of Two Methods for Recovering the Release History of a Groundwater Contamination Source(Master Dissertation)New Mexico Institute of Mining and Technology,Socorro,New Mexico,1999.

[22]D.L.Ma,Z.X.Zhang,Leakage source parameters identification for CO2sequestration based on Occam method,Energy Procedia 63(2014)3815-3820.

[23]F.Bozzoli,L.Cattani,S.Rainieri,F.S.Bazán,L.S.Borges,Estimation of the local heat transfer coefficient in the laminar flow regime in coiled tubes by the Tikhonov regular is ation method,Int.J.Heat Mass Transf.72(2014)352-361.

[24]H.Wei,W.J.Dang,S.Wei,Parameter identification of solute transport with spatial fractional advection-dispersion equation via Tikhonov regularization,Optik 129(2017)8-14.

[25]Z.M.Yuan,Z.B.Deng,M.Z.Jiang,Extended partial blockage detection in a gas pipeline based on Tikhonov regularization,J.Nat.Gas Sci.Eng.27(Part 1)(2015)130-137.

[26]P.Kathirgamanathan,Source Parameter Estimation of Atmospheric Pollution from Accidental Releases of Gas(Ph.D.Thesis)Massey University,New Zealand,2003.

[27]R.C.Aster,B.Borchers,C.H.Thurber,Parameter Estimation and Inverse Problems,Second edition Elsevier Inc.,Oxford,2013.

[28]C.P.Hansen,Rank-De ficient and Discrete ill-Posed Problems,SIAM,Philadelphia,PA,1997.

[29]S.R.Hanna,G.A.Briggs,R.P.Hosker,Handbook on Atmospheric Diffusion,U.S.Department of Energy,Technical Information Center,USA,1982.

[30]M.L.Barad,Project prairie grass,a field program in diffusion,Geophysical Research,Paper 1(59),Air Force Cambridge Centre,Massachusetts,USA,1958.