铝蜂窝填砂复合夹芯结构的低速冲击响应试验研究
罗伟铭,石少卿,孙建虎, 刘盈丰
(1.陆军勤务学院 军事设施系,重庆 401331; 2.重庆对外建设(集团)有限公司,重庆 401121)
铝蜂窝夹芯结构由于自身优良的力学性能和吸能特性,被广泛应用于航天[1],防护,汽车,船舶[2]以及其他领域。其复合形式一直是研究的热点,主要的复合方法一般包括如下三种:首先,利用不同的面板材料,例如碳纤维面板、玻纤面板等,Belingardi等[3]研究了碳纤维面板和铝蜂窝芯组合的复合夹芯梁在四点弯曲条件下的疲劳损伤;Akatay等[4]利用玻璃纤维增强环氧树脂作为面板,铝蜂窝芯作为芯层,制作出具有较好抗冲击性能的夹芯结构;其次,为了提升复合结构力学性能,可采用不同的芯层例如蜂窝芯,格架芯[5-6],泡沫芯[7],软木芯[8]等等,其中蜂窝芯的材料又可以分为铝、PP聚丙烯、NOMEX诺梅克斯[9-10]、纸[11]等等;另外,在结构形式上可采用多种复合方法,包括组合型、填充型、增强型。Han等[12]通过采用蜂窝-瓦楞混合的组合形式,在铝制瓦楞芯的空隙中填充铝蜂窝块,制作了一种新型的复合夹芯结构,利用准静力面外压缩试验来验证结构的力学性能,结果表明该混合结构的强度和吸能水平强于瓦楞和蜂窝二者的总和。另外,填充的复合形式也较为常见,例如Mozafari等[13]对蜂窝夹芯结构填充聚氨酯泡沫后吸能水平和冲击强度的提升进行了量化研究,值得一提的是,他们用的结构面板是抗冲击性能更佳的编织复合材料。Zhang等[14]研究了聚氨酯泡沫填充金字塔型格架芯夹芯结构的低速冲击性能和吸能特性,发现填充泡沫后,冲头与试件接触时间减短,峰值力提高。Shi等[15]采用在铝蜂窝芯中增加正交铝肋的方法,以弥补碳纤维面板和铝蜂窝芯刚度不对称的缺陷,减小界面错动,通过三点弯曲试验验证后,结果表明该方法达到提升夹芯结构力学特性的目的;同时他们还研究了利用短凯夫拉纤维来增强碳纤维面板和铝蜂窝芯的界面强度,通过三点弯曲试验和面内压缩试验证明该方法具有可行性和有效性,界面增强后的试件具有更高峰值力和吸能性能[16]。
本文以防护结构设计为背景,受芯层填充方法的启发,提出一种铝蜂窝填砂复合夹芯结构,结构如图1所示。目前,尚未发现铝蜂窝填砂复合夹芯结构力学性能研究的相关报道,本文从理论角度对填砂蜂窝模型进行力学分析,通过落锤冲击试验,对不同芯层规格的试件在梯度能级冲击下的响应进行了对比,根据荷载、位移和挠度的变化规律,以及结构的破坏模式来分析芯层填砂对结构冲击响应的影响。
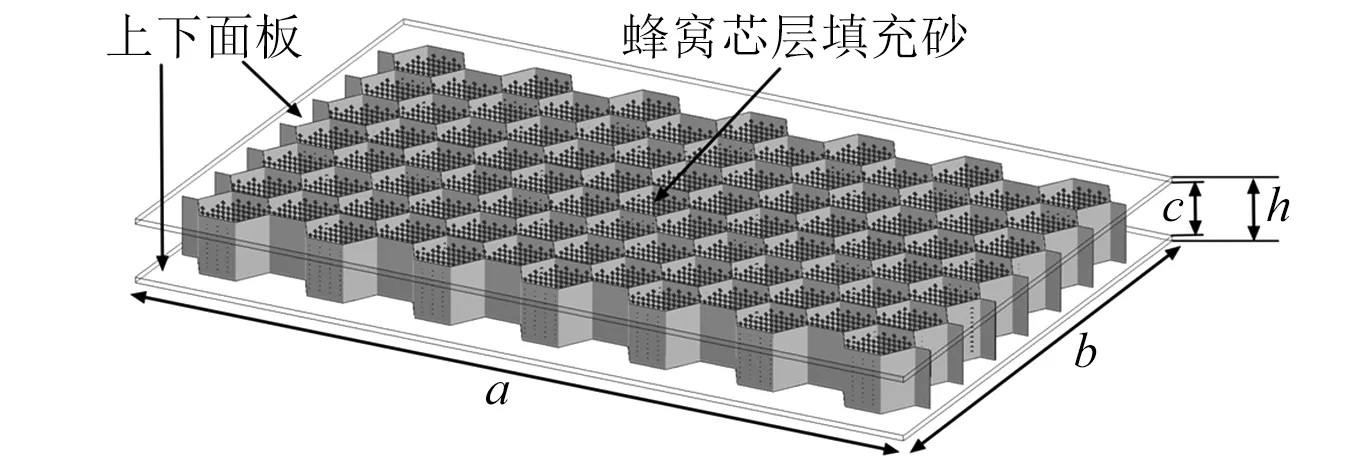
图1 铝蜂窝填砂复合夹芯结构示意图Fig.1 Schematic description of the sand-filled aluminum honeycomb sandwich structure
1 理论分析
蜂窝结构是一种周期性多胞结构,因此,研究其力学特性可以取单个分析模型进行研究[17],如图2中右侧几何体所示。
铝蜂窝填砂复合夹芯结构受面外冲击作用时,冲击点及周围局部区域主要发生压缩变形,该局部向周围扩展的区域会发生剪切变形,当冲击能量很大时,大部分区域甚至发生压剪混合变形。因此,可对分析模型的受力情况进行分解,如图3所示,图3(a)为分解后的压缩变形情况,图3(b)为分解后的剪切变形情况。当变形处于弹性阶段时,将分析模型对压应力和剪应力的反作用力σ′和τ′分解为:
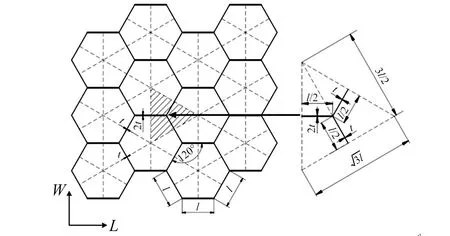
图2 蜂窝分析模型[17]Fig.2 Analysis model of honeycomb
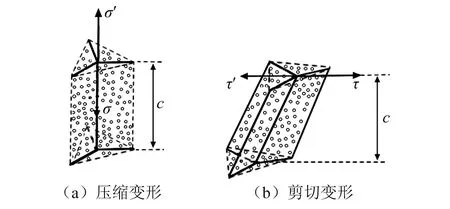
图3 填砂蜂窝分析模型压剪变形受力分析Fig.3 Force analysis of the model of sand-filled honeycomb
(1)
式中:σhe和τhe为铝蜂窝的弹性坍塌应力和弹性剪切应力;σs和τs为砂提供的承载应力和剪切应力;α和β为砂和铝蜂窝的相互作用力系数;铝蜂窝单片铝箔轴向弹性屈曲荷载由其二阶惯性矩和胞元边长l决定[18]:
(2)
式中:K为胞元端面约束因子;Eh和νh分别为铝箔材料弹模和泊松比;t为蜂窝铝箔厚度;根据图2所示,取出的分析模型三角形面积Ah为:
(3)
由此计算出其弹性坍塌应力σhe为:
(4)
又根据砂的力学特性又可将等式(1)中的σ′等效为:
(5)
式中:σcp为分析模型中砂所受侧限应力;φs为砂的内摩擦角。由于蜂窝自身的几何特性,导致其弹性剪切应力τhe存在方向性,τhe在图2中L和W方向上的剪应力分别为:
(6)
式中:C为常数;θ为相邻铝箔所夹锐角。当蜂窝变形进入稳态塑性阶段,式(1)中的σhe会变成塑性坍塌应力σhp可近似为:
(7)
式中:σy为材料的屈服应力。赵国伟等[19]还在已有的蜂窝结构静态平均塑性坍塌应力理论模型和Cowper-Symonds本构模型的基础上,建立了具有应变强化效应的平均塑性坍塌应力理论模型:
(8)
式中:k为常数;v为冲击加载速度;C和p为应变率敏感系数;Ep为塑性硬化模量。由此可以看出,蜂窝的材质和几何参数、砂的性质和填充密度、砂和蜂窝的相互作用以及冲击的能级和速度均会影响其响应结果,同时,结构在不同能级冲击下,材料进入弹塑性阶段的时间和程度不同均会导致不同的响应结果。理论分析结果为落锤冲击试验的变量设置提供依据。
2 落锤冲击试验
2.1 材料选择
本文采用ASTM D 7136标准来进行落锤冲击试验。根据理论分析结果,利用控制变量法,将试验中的多变量变成单变量进行分析。因此,为保证材料统一,所有试件蜂窝芯均采用AL3003-H18制作,铝箔厚度t均为0.04 mm,以AL-5052-H32作为面板,面板厚度均为1 mm。AL3003-H18和AL-5052-H32材料属性如表1所示。
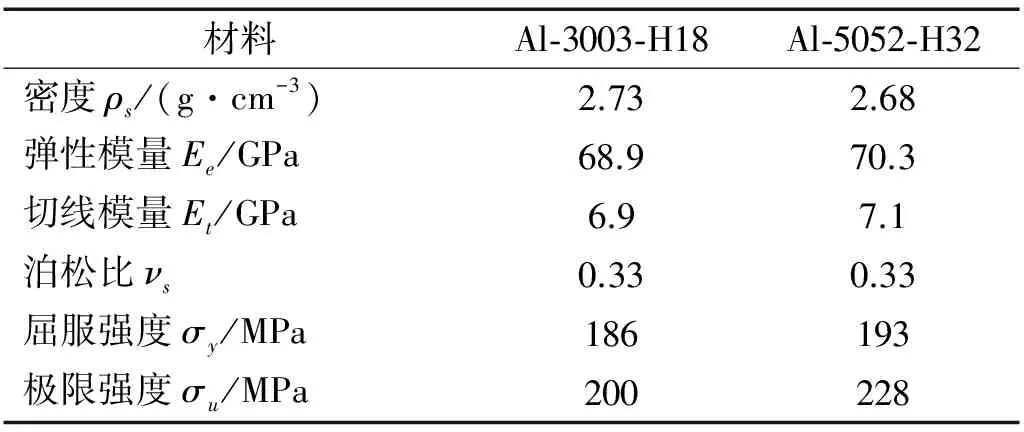
表1 面板和蜂窝芯材料力学特性参数Tab.1 Mechanical properties of base materials for facesheets and honeycomb core
试验所采用的夹芯结构类型包括以下四种:A,B,B1,B2。根据图2中的分析模型可以计算出蜂窝的相对密度为:
(9)
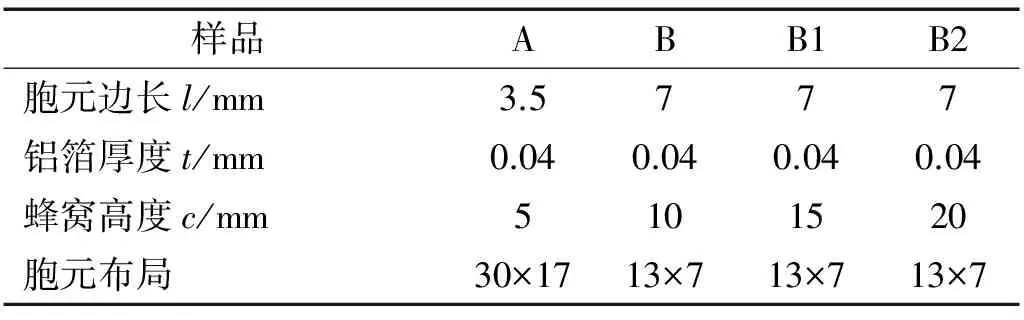
表2 芯层蜂窝尺寸Tab.2 Honeycomb size
式中:ρh为蜂窝密度;ρb为铝箔材料密度。为了将蜂窝芯几何尺寸定为独立变量,根据式(9)将A和B的蜂窝芯设置为如表2所示的尺寸,使其质量相同。而B, B1和B2的蜂窝尺寸相同,高度设置为独立变量。填砂试件如图4所示(未加上面板时)。为了对比芯层填砂对铝蜂窝夹芯结构的影响,同工况下,试件均分为两组:一组空芯和一组填砂。填砂方式采用自然堆积,以保证所有试件具有相同的填充密度。如图2所示,对于六边形蜂窝,蜂窝L(带向)剪切性能大约是W(横向)的2倍,因此,蜂窝芯沿试件长度方向选择L向。

图4 试验试件Fig.4 Specimens of test
2.2 试验方法
落锤冲击试验采用Instron Dynatup 9250 HV试验机。冲头加砝码总质量为10.09 kg,冲头的冲击端部为直径12.7 mm的半球形球头。根据标准,试件切割成150 mm×100 mm尺寸后,夹持在固定支座上,该支座平台的几何中心有125 mm×75 mm方形开孔。整个冲击过程的力和冲头位移通过力传感器和位移传感器自动采集,再由脉冲数据采集软件记录。冲击试验机、冲头以及固定支座和夹具如图5所示。
3 结果与分析
3.1 冲击响应
为了测试铝蜂窝填砂复合夹芯结构的低速冲击响应,落锤冲击试验中设置了四个能级的冲击能量,初始设置值为25 J,50 J,100 J,150 J,但由于试验机的初始设置值和最终实测值存在一定误差,因此,最终的冲击能量以实测为准,分别为17 J,39 J,83 J,119 J。设置四种冲击能级的目的是为了从梯度增长的冲击能量下获取和发现冲击响应的变化规律。为了参照对比,将17 J和39 J设定为低能级,83 J和119 J设定为高能级。低能级下,A和B型夹芯结构作对比,考察蜂窝尺寸对冲击响应的影响;高能级下,B、B1和B2型夹芯结构作对比,考察蜂窝高度变化产生的影响。

图5 试验设置Fig.5 Experimental setup
从图6可见:低能级冲击下,每组曲线的峰值和位移均会随着冲击能量的增加而增加;填砂之后的力-位移曲线峰值升高,冲头终止位移减小,同时曲线变得相对光滑,而空芯试件对应的曲线会出现抖动,尤其是B型空芯试件的两组工况,这是因为空芯试件在受冲击过程中,当冲击力到达蜂窝芯屈曲强度后产生屈曲变形,随后结构产生一定弯曲挠度,因此整个过程的曲线会产生抖动,关于试件的破坏模式下面会详细描述;B型填砂试件的力-位移曲线峰值增幅和位移减小幅度均比A型的大,这是由于A型试件的胞元尺寸小,面外和面内强度高于B型试件,换句话说,B型试件芯层相对A较软,因此,填砂对于B型试件强度提升和变形挠度减小的作用要相对大一些;值得注意的是,A和B型填砂试件力-位移曲线峰值和终止位移几乎相同,而A型试样填砂量约为B型试样的1/2,因此,在低能级冲击作用下,可优先选择胞元较小高度较低的蜂窝作为填砂复合夹芯结构的芯层。
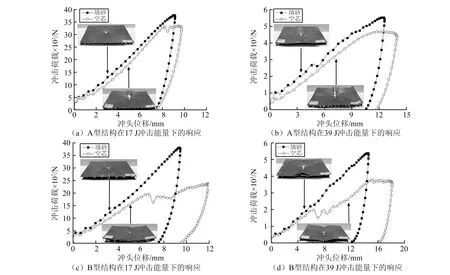
图6 低能级冲击响应Fig.6 Impact responses in low energy level
如图7所示,在高能级冲击作用下,力-位移曲线同样在填砂之后呈现出峰值升高,冲头终止位移减小;并且,可以看出每组空芯试件的曲线均会在初期(位移6 mm~8 mm之间)出现一个小峰值(1.5 kN~2.5 kN),如图7中所有空芯试件曲线所示,这是蜂窝芯发生屈曲变形引起的,经对比发现,蜂窝芯发生屈曲变形的临界值会随着高度增加而减小;其次,图7的(b), (d), (e), (f)的空芯试件曲线以及(f)中的填砂试件曲线在冲击过程后期出现一个较大的峰值,该值是由于冲头已经完全穿透上下面板,冲头后部的加粗杆接触到上面板,防止冲头进一步穿透造成的,因此,该峰值可不计入冲击响应;相比较而言,填砂之后,力-位移曲线由于冲头接触上面板迅速进入峰值,随后抖动减小,图7中(c), (d), (e), (f)填砂试件曲线较为明显,这是产生的峰值力,穿透上面板后与蜂窝以及砂之间相互作用产生的抖动。
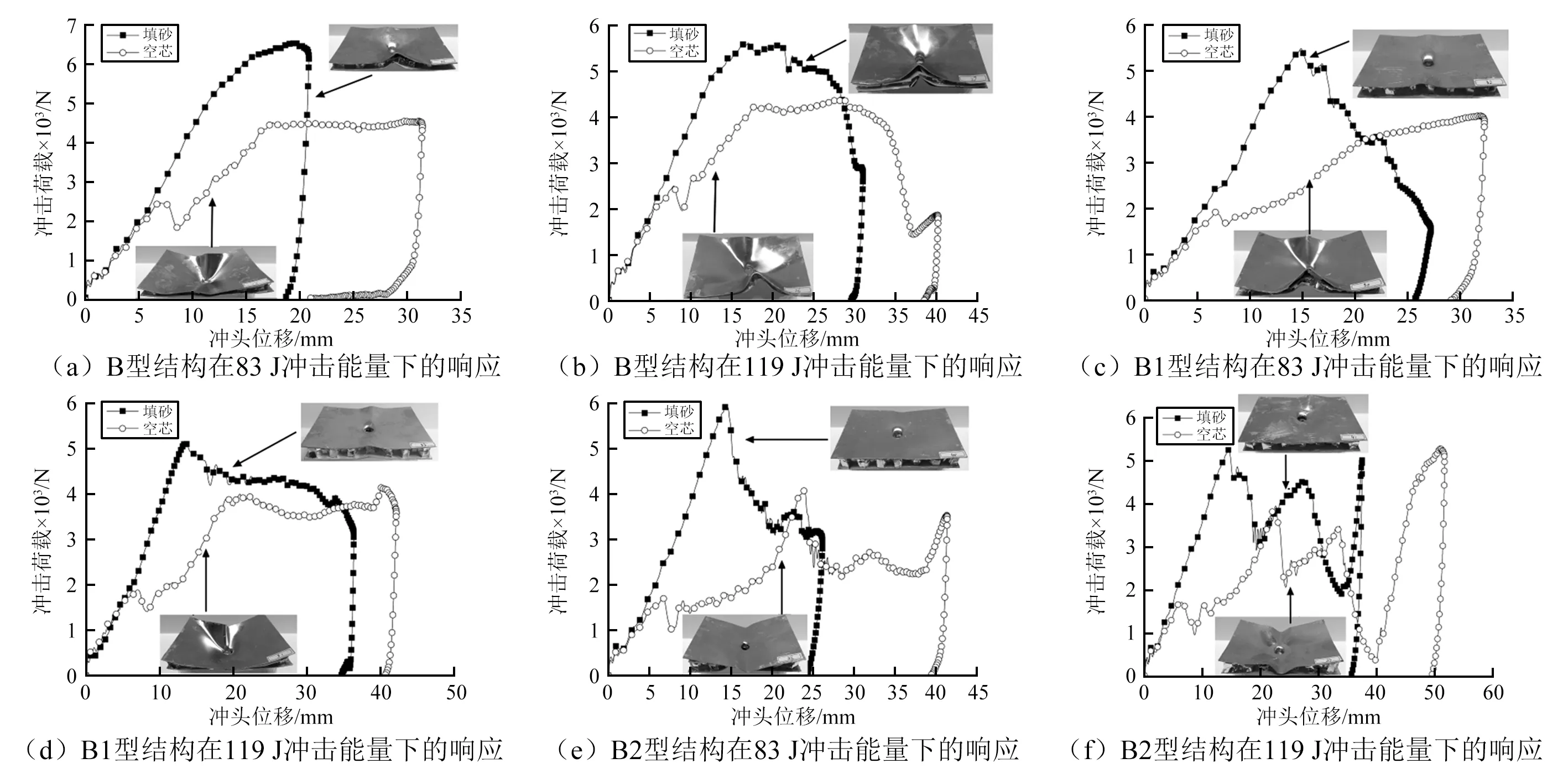
图7 高能级冲击响应Fig.7 Impact responses in high energy level
3.2 荷载、位移和挠度
如图8所示,随着冲击能量的增加,冲击峰值力的变化具有一定的规律,低能级冲击作用下(17 J~39 J),随着冲击能量增加,冲击峰值力增势明显,从低能级向高能级过渡过程中(39 J~83 J),尽管峰值继续增加,但增势减弱,进一步增加冲击能量后(83 J~119 J)峰值却出现下降,这是由于低能级冲击状态下,冲头仅在结构上面板造成球形凹痕,结构产生一定的挠度,因此峰值会随着冲击能量的增加而增加,而低能级向高能级过渡后,上面板出现裂缝或者穿透,因此峰值力增势减小,冲击能量增加到最大时,冲头贯穿结构,因此峰值力降低。由此推断,全贯穿临界值应当介于83 J~119 J之间。如图9所示,增加冲击能量会导致冲头终止位移量增加,这和试件的变形破坏有关,当冲头完全贯穿试件后,其位移就会增加很多,因此曲线在高能级阶段(83 J~119 J)增势明显。通过测量结构下面板变形挠度发现,低能级阶段和过渡阶段,挠度随冲击能量的增加表现出一种线性增长,但在高能级阶段出现分化,即空芯试件的变形挠度随着冲击能量的增加而增加,但填砂试样中B1和B2的变形挠度却减小,其中B型试件的变形挠度继续保持线性增加,如图10所示。由此可以推断,当结构芯层填砂之后,其高度达到一定的值时,变形挠度将减小。

图8 峰值力变化规律Fig.8 The change law of peak force
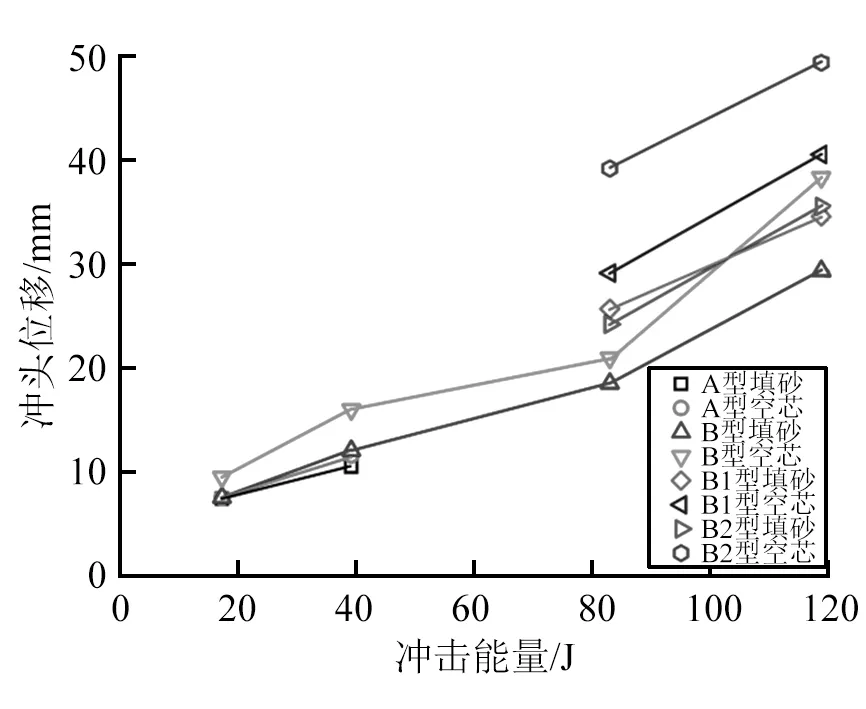
图9 冲头位移变化规律Fig.9 The change law of impactor displacement

图10 变形挠度变化规律Fig.10 The change law of deflection
3.3 破坏模式
通过对比落锤低速冲击后试件的变形和破坏情况,发现试件受到冲击能级和芯层填砂的影响,其破坏模式基本可分为4种。首先,低能级冲击作用下,填砂试件的整体变形较小,冲头均会在上面板中心留下球形凹痕,如图11(a)所示的Ⅰ型模式;高能级冲击作用下,试件两侧边缘的中间位置会产生比较大的褶皱形翘曲,如图11(b)所示的Ⅱ型模式;对于B1和B2型夹芯结构,空芯试件和填砂试件的区别较为明显,B1型空芯试件在高能级冲击作用下发生Ⅱ型模式变形,B2型则从中间产生一条横向凹陷,如图11(c)的Ⅲ型模式,产生该变形的原因主要由于冲击力达到蜂窝芯发生屈曲变形的临界值,蜂窝压缩屈曲后结构中间部分变薄,如同简支梁中点受冲击产生塑性铰一样,形成整体弯曲变形,而B1和B2型填砂试件由于整体刚度较大,变形较小,冲头形成局部贯穿破坏,破坏模式如图11(d)的Ⅳ型。

图11 破坏模式Fig.11 Damage modes
4 结 论
本文提出一种铝蜂窝填砂复合夹芯结构,对填砂蜂窝模型进行了力学分析,在设计的20组工况下对其低速冲击响应进行落锤冲击试验研究,结果表明:
(1)根据分析模型受力情况可知,铝蜂窝的材质和几何参数、砂的性质和填充密度、砂和蜂窝的相互作用、冲击的能级和速度均会影响其响应结果;而针对具体试验结构,通过变量控制后影响其性能的主要因素为胞元边长l、蜂窝高度c、砂的力学性能以及冲击能级,其中l的减小和c的增加对结构抗冲击性能产生有利影响。
(2)在低能级冲击作用下,蜂窝芯层较软的试件填砂后对于其结构强度和刚度的提升作用较为明显,同时,在铝蜂窝质量相同的前提下,优先选择蜂窝胞元较小、高度较低的蜂窝作为填砂复合夹芯结构的芯层,可减少芯层填砂量,提高结构比强(刚)度,而具体尺寸的设定将在今后的研究中得到优化。
(3)在高能级冲击作用下,当芯层高度达到一定值时,对比空芯试件,变形挠度减小,破坏范围缩小为局部贯穿破坏,芯层填砂对结构抗冲击性能产生较为积极的影响。
参 考 文 献
[1] 胡建国, 马大为, 乐贵高, 等. 蜂窝材料率相关本构模型及其在月球探测器中的应用研究[J].振动与冲击, 2014, 33(7): 114-119.
HU Jianguo, MA Dawei, LE Guigao, et al.A rate-dependent constitutive model for honeycomb material and its application in lunar lander [J].Journal of Vibration and Shock, 2014, 33(7): 114-119.
[2] 任鹏, 张伟, 刘建华, 等.水下冲击波作用的铝合金蜂窝夹层板动力学响应研究[J].振动与冲击, 2016, 35(2): 7-11.
REN Peng, ZHANG Wei, LIU Jianhua, et.al.Dynamic analysis of aluminum alloy honeycomb core sandwich panels subjected to underwater shock loading[J].Journal of Vibration and Shock, 2016, 35(2): 7-11.
[3] BELINGARDI G, MARTELLA P, PERONI L.Fatigue analysis of honeycomb-composite sandwich beams[J].Composites Part a Applied Science & Manufacturing, 2007, 38(4): 1183-1191.
[4] AKATAY A, BORA M Ö, ÇOBAN O, et al.The influence of low velocity repeated impacts on residual compressive properties of honeycomb sandwich structures[J].Composite Structures, 2015, 125: 425-433.
[5] YANG J S, MA L, SCHMIDT R, et al.Hybrid lightweight composite pyramidal truss sandwich panels with high damping and stiffness efficiency[J].Composite Structures, 2016, 148: 85-96.
[6] ZHANG G, WANG B, MA L, et al.Energy absorption and low velocity impact response of polyurethane foam filled pyramidal lattice core sandwich panels[J].Composite Structures, 2014, 108(1): 304-310.
[7] MOHMMED R, ZHANG F, SUN B, et al.Static and low-velocity impact on mechanical behaviors of foam sandwiched composites with different ply angles face sheets[J].Journal of Composite Materials, 2014, 48(10): 1173-1188.
[8] WANG H, RAMAKRISHNAN K R, SHANKAR K.Experimental study of the medium velocity impact response of sandwich panels with different cores[J].Materials & Design, 2016, 99: 68-82.
[9] ZHANG T, YAN Y, LI J, et al.Low-velocity impact of honeycomb sandwich composite plates[J].Journal of Reinforced Plastics & Composites, 2015, 35(1):1-25.
[10] 彭蒙, 刘龙权, 赵剑,等.芯体壁厚对Nomex蜂窝夹层结构抗冲击性能的影响[J].振动与冲击, 2016, 35(21): 177-182.
PENG Meng, LIU Longquan, ZHAO Jian, et.al.Effect of resin layer thickness on impact resistance performance of nomex honeycomb sandwich structures[J].Journal of Vibration and Shock, 2016, 35(21): 177-182.
[11] WANG D, BAI Z.Mechanical property of paper honeycomb structure under dynamic compression[J].Materials & Design, 2015, 77: 59-64.
[12] HAN B, QIN K, YU B, et al.Honeycomb-corrugation hybrid as a novel sandwich core for significantly enhanced compressive performance[J].Materials & Design, 2016, 93: 271-282.
[13] MOZAFARI H, KHATAMI S, MOLATEFI H.Out of plane crushing and local stiffness determination of proposed foam filled sandwich panel for korean tilting train express-numerical study[J].Materials & Design, 2015, 66: 400-411.
[14] ZHANG G, WANG B, MA L, et al.Energy absorption and low velocity impact response of polyurethane foam filled pyramidal lattice core sandwich panels[J].Composite Structures, 2014, 108(1): 304-310.
[15] SHI S S, SUN Z, HU X Z, et al.Flexural strength and energy absorption of carbon-fiber-aluminum-honeycomb composite sandwich reinforced by aluminum grid[J].Thin-Walled Structures, 2014, 84: 416-422.
[16] SHI S S, SUN Z, HU X Z, et al.Carbon fiber and aluminum honeycomb sandwich composites with and without Kevlar-fiber interfacial toughening[J].Composites Part A Applied Science & Manufacturing, 2014, 67: 102-110.
[17] 王闯, 刘荣强, 邓宗全, 等.铝蜂窝结构的冲击动力学性能的试验及数值研究[J].振动与冲击, 2008, 27(11): 56-61.
WANG Chuang, LIU Rongqiang, DENG Zongquan, et al.Experimental and numerical studies on aluminum honeycomb structure with various cell specifications under impact loading[J].Journal of Vibration and Shock, 2008, 27(11): 56-61.
[18] ZHANG J, ASHBY M F.The out-of-plane properties of honeycombs[J].International Journal of Mechanical Sciences, 1992, 34(6): 475-489.
[19] 赵国伟, 白俊青, 祁玉峰, 等.异面冲击下金属蜂窝结构平均塑性坍塌应力模型[J].振动与冲击, 2016, 35(12): 50-54.
ZHAO Guowei, BAI Junqing, QI Yufeng, et.al.Average plastic collapse stress model of metallica honeycomb structure under out-of-plane impact load[J].Journal of Vibration and Shock, 2016, 35(12): 50-54.

