面向真彩色三维显示的分层角谱算法和Gerchberg-Saxton算法研究∗

范爽 张亚萍 王帆 高云龙 钱晓凡 张永安 许蔚 曹良才

1)(昆明理工大学理学院,昆明 650500)

2)(昆明理工大学建筑工程学院,昆明 650500)

3)(清华大学精密仪器系,精密测试技术及仪器国家重点实验室,北京 100084)

1 引 言

计算全息较之传统光学全息省去了光源、记录介质和光学平台等硬件,噪声低,可复制性高,可计算虚拟物体,具有极大的灵活性[1−6],可为理想的真三维显示技术提供技术支持.计算三维物体的全息图的基本算法主要有:点源法[7]、面元法[8,9]、层析法[10]以及在频域中进行计算的角谱法[11,12]等.目前的研究主要致力于面向复杂形貌三维物体提高再现像质量和计算速度.

在改善全息图重建像质量方面,2004年,北京理工大学谢敬辉等[10]提出了菲涅耳波带板扫描全息术,成功地计算了三维物体的全息图,并通过数字高通滤波抑制了背景噪声,提高了成像质量;2005年,华沙理工大学Michal等[13]提出用迭代菲涅耳算法计算三平面的相位型全息图,计算简单物体,迭代10000次,再现像存在2.5倍噪声;2014年,北京邮电大学曹雪梅等[14]提出利用二维彩色图像和深度图生成菲涅耳计算全息图,强度叠加80次,成功地进行了复杂彩色三维场景的全息记录和再现;2015年,东南大学Chang等[15]提出像面上的振幅和相位被理想的振幅和统一的相位所取代的双重约束的Gerchberg-Saxton(GS)算法,与传统的GS算法相比,相同迭代次数下,同一物体重建像的散斑噪声对比度降低41.7%,提高了成像质量;2017年,中国科学院光电技术研究所Pang等[16]在此基础上提出在物面和全息面之间加入两倍物面大小的虚拟媒介平面的分层迭代算法,计算简单物体的再现像,其相位的均方根误差(RMSE)在迭代800次后可近似收敛为0,再现像质量得到了大幅提升.在提高计算速度方面,2015年,清华大学Zhao等[17]提出分层角谱算法,同一硬件条件下计算同一复杂三维物体,与传统点源法相比,计算负载大大降低,计算速度提高约860倍.

本文基于分层角谱算法分析了在真彩色物体计算方面的多波长采样,实现了彩色物体的分层角谱算法,并得到清晰的再现像;同时,为了消除算法实施过程中严重的散斑噪声,引入GS算法[18],提出基于分层角谱的GS算法,有效地抑制散斑噪声,提高再现像质量,并通过计算引入GS算法前后再现像的RMSE和峰值信噪比(PSNR)加以证明.同时,相比于双重约束的GS算法[15]和分层迭代算法[16],该算法编码复杂度更低,对复杂形貌三维物体的计算可有效提高算法速度.

2 真彩色物体的分层角谱算法

2.1 分层角谱算法的数学模型推导

分层角谱算法的基本物理模型是将三维物体沿深度方向离散成s个相互平行的平面,各层物面需附加随机相位以防止物光波频谱信息丢失,再将每一层物面通过平面波角谱理论衍射到达全息面后进行叠加,即可得到整个三维物体的物光场,进而求得全息图,物理过程如图1所示,其中hj是第j层物面的全息图.

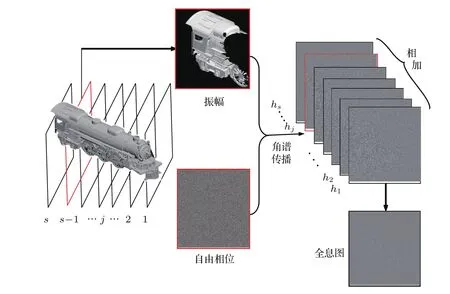
图1 分层角谱算法的原理[17]Fig.1.Principle of angular-spectrum layer-oriented method[17].

假设三维物光场的复振幅为

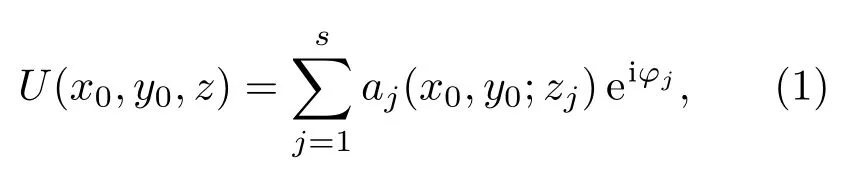
其中,(x0,y0,z)是物光场的坐标,j是层的序号,s是层的总数,aj为第j层的振幅,zj为第j层物面的深度值,k是波数,φj是第j层物面的随机相位.

平面波角谱算法的传递函数为

在平面波角谱理论中,平面波在自由空间中传播时,其波面形状不发生改变,仅产生一个与传播距离有关的相移[19].每一层衍射物面的角谱函数乘以一个对应的与传播距离相关的传递函数,得到该衍射物面在全息面上的角谱函数为

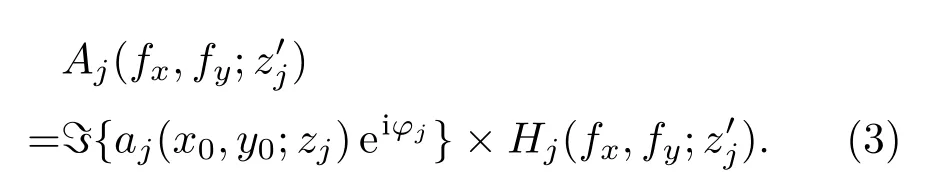
将进行傅里叶逆变换得到该衍射物面的全息图,所有物面的全息图叠加得到整个三维物光场的全息图,其复振幅为

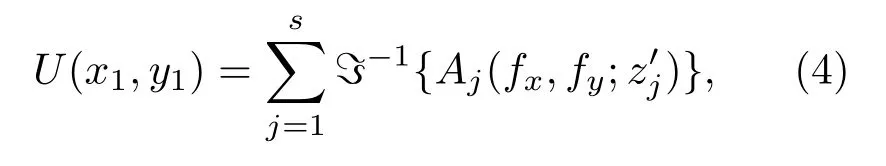
其中,(x1,y1)是全息面的坐标,ℑ表示二维傅里叶变换,ℑ−1是二维傅里叶逆变换.

2.2 真彩色分层角谱算法的仿真计算

分层角谱算法主要根据三维物体深度图的灰度数据进行分层,首先将实际采集或软件生成的三维物体,通过计算机图形学方法得到其强度图和深度图;或三维物体的二维平面图像通过立体匹配技术得到图像的视差,再利用视差图得到相应的深度图[14].深度图的灰度变化表示三维物体的深度变化,8 bit深度图像即存在28=256个灰度值,物体可分为256层,每一层均采用平面波衍射角谱理论进行计算得到子全息图,将子全息图叠加成整个物体的全息图[17],最后加入参考光重建三维物光场.

在实现真彩色分层角谱算法时,由于红、绿、蓝三色光的波长不同,为了避免混频现象,采样首先要满足奈奎斯特采样定理.

一维传递函数为

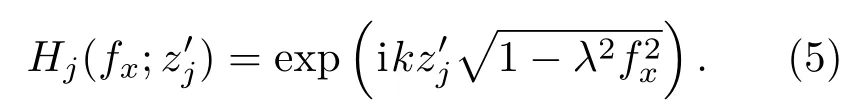
其相位分布的局域空间频率表示为[17]

采样间隔应满足奈奎斯特采样定理[12],得到

设物面尺寸L=∆x·N,∆x为采样间隔,N为采样点数,当最大频率fxmax=N/(2L)时,有效衍射距离为

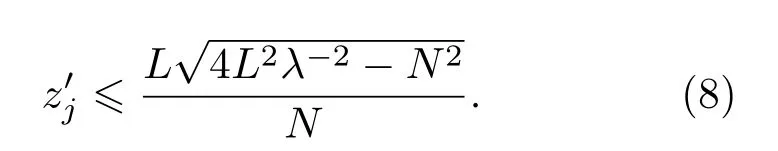
根据(8)式的计算可知,当各层物面的采样间隔∆x和采样点数N都相同且确定时,各层物面的尺寸L也相同且确定,这时为避免混频现象,有效衍射距离的取值应为λ=λR=625 nm时的值.

利用计算机图形学绘制一套彩色茶具,并通过渲染技术得到茶具强度图和深度图,分别对应于茶具的振幅信息和深度信息,如图2(a)和图2(b)所示.

首先,根据深度图的灰度值范围将茶壶和茶杯分为两个大的层面,每层物面都附加随机相位,当深度图和强度图的∆x=8µm,N=1920时,L=15.36 mm,所以设远处茶杯的近处茶壶的然后,设红、绿、蓝三个波长分别为λR=625 nm,λG=532 nm,λB=473 nm.将强度图分解为R,G,B三基色图像,如图3(a)—(c)所示.

将三基色图分别采用分层角谱算法计算对应的相位型全息图,如图4所示.

图2 彩色茶具 (a)强度图;(b)深度图Fig.2.Colorful tea set:(a)Intensity map;(b)depth map.

图3 茶具的三基色图 (a)R基色图;(b)G基色图;(c)B基色图Fig.3.Three color images of tea set:(a)R-based color map;(b)G-based color map;(c)B-based color map.

最后,选择垂直平面参考光R=1,分别对每个相位全息图进行模拟重构,生成对应颜色分量的重构结果,使用图像处理的方法将其合成彩色图像[20],其数值模拟结果如图5所示.

由图5(a)和图5(b)所示的重构结果得出该方法可成功地对复杂彩色三维场景进行全息记录与再现.相较于文献[14]中的方法而言,该方法不用多次进行强度叠加即可得到较为清晰的再现像,提高了计算速度;同时,平面波角谱理论的应用避免了单次菲涅耳衍射过程中波长不同导致的衍射角大小不同,最终影响单色全息重构像的尺寸大小,也避免了菲涅耳衍射存在的傍轴近似和大数值孔径系统中较为严重的计算误差.但是,三维物体深度图的准确性会直接影响再现像的准确性[21],且在实验中仍要考虑波长不同引起的色差,一般采用消色差傅里叶透镜解决这类问题.从图5(a)和图5(b)可以看出,由于随机不稳定的相位分布导致临近采样点的相位起伏波动大,再现像存在一些散斑噪声.

为抑制散斑噪声可以将物光和会聚光结合,但生成的全息图中会有边缘振荡效应,分辨率低[16].所以,本文进一步引入GS算法,提出基于分层角谱的GS算法的模型,用于计算复杂形貌的三维物体,有效地抑制散斑噪声,降低算法复杂度.

图4 茶具的三基色图对应的全息图 (a)R通道全息图;(b)G通道全息图;(c)B通道全息图Fig.4.Corresponding holograms of three color images of tea set:(a)R-channel hologram;(b)G-channel hologram;(c)B-channel hologram.

图5 彩色分层角谱算法的数值模拟结果 (a)在180 mm处再现像;(b)在240 mm处再现像Fig.5.Numerical simulation results of colorful angular-spectrum layer-oriented algorithm:(a)The reconstruction of image at 180 mm;(b)the reconstruction of image at 240 mm.

3 基于分层角谱算法的GS算法

传统GS算法[22−24]的目标物体是二维平面图像.首先,通过傅里叶变换生成目标图像的全息图.然后,全息图的相位不变,振幅用常数调制得到调制后的全息图,该全息图通过逆傅里叶变换得到再现像;再现像的相位不变,振幅用目标图像振幅调制得到调制后的再现像,该再现像再通过傅里叶变换得到全息图,如此构成一个循环.最后,当迭代次数达到设定的值时,输出全息图的相位,再现原物体.

三维GS算法是在传统GS算法的基础上,将一个二维物平面变为由不同深度的二维物平面组成的三维物体,因为三维物体涉及深度信息,所以将迭代中的傅里叶变换和逆傅里叶变换改成与深度有关的菲涅耳衍射和逆菲涅耳衍射[25,26],如图6所示.

根据三维GS算法的原理,将其与分层角谱算法结合,光在全息面与物面之间传播可以用平面波角谱衍射代替菲涅耳衍射,分层角谱GS算法的流程图如图7所示.

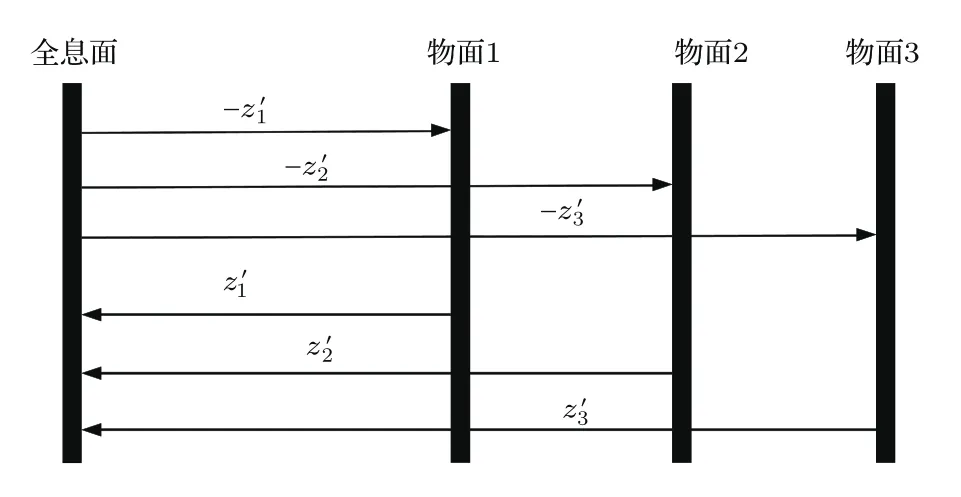
图6 三维GS算法Fig.6.Three-dimensional GS algorithm.

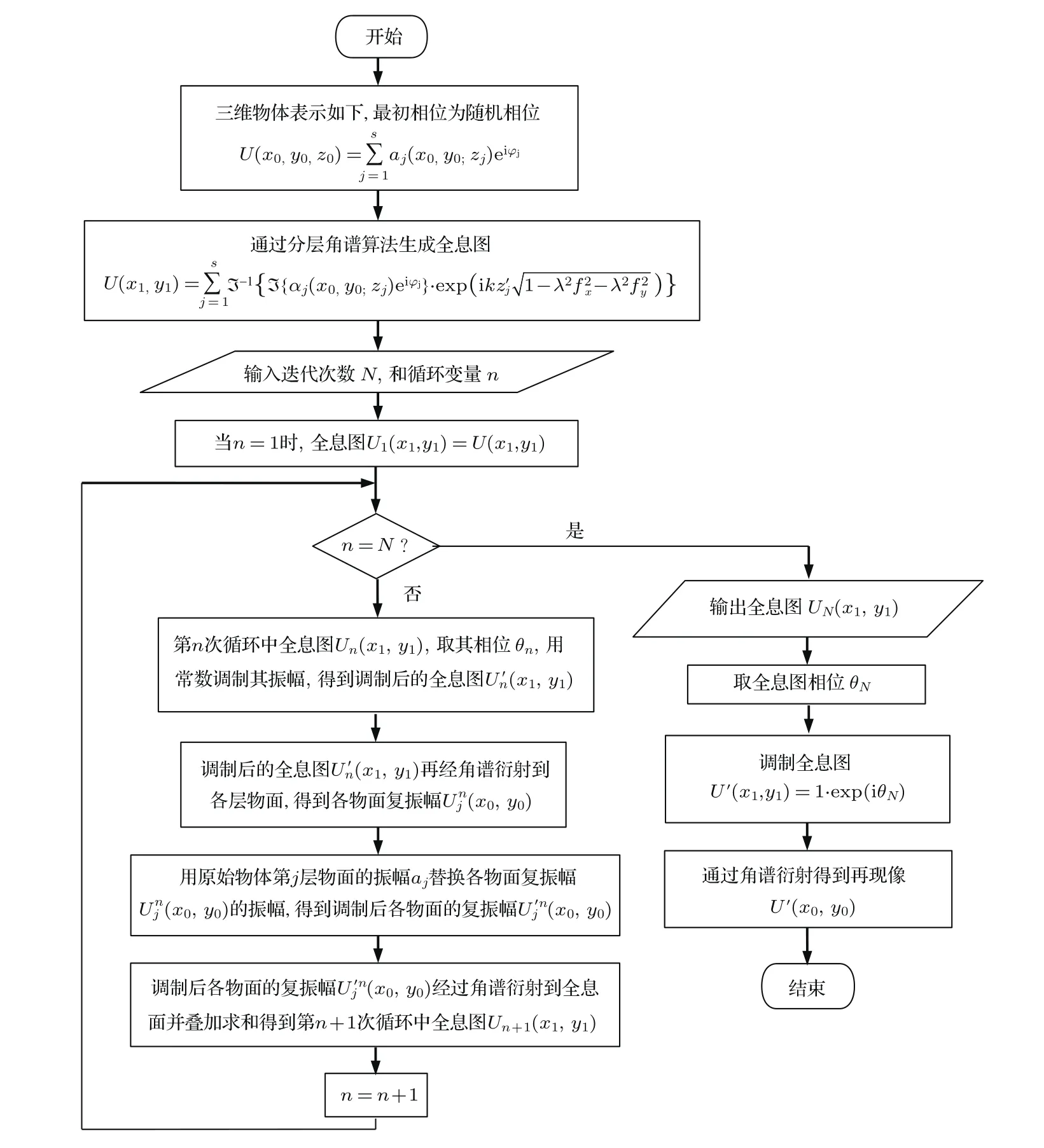
图7 基于分层角谱法的GS算法Fig.7.GS algorithm based on angular-spectrum layer-oriented method.

首先设第n次循环中全息图的复振幅为Un(x1,y1),当n=1时,U1(x1,y1)=U(x1,y1).取第n次循环中全息图的相位θn:

其中,angle{·}表示求相位的操作.用常数1替换第n次循环中全息图的振幅,得到调制后的第n次循环的全息图:

再将调制后的全息图通过平面波角谱衍射传到各层物面,得到第n次循环中各层物面的复振幅,其中第j层物面的复振幅为

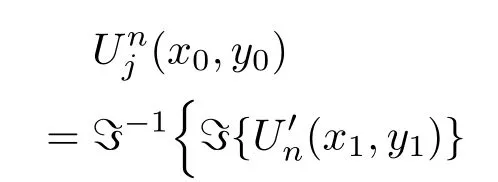
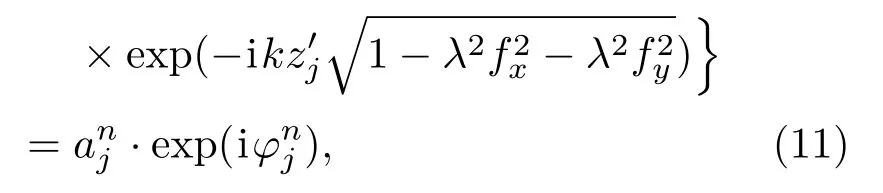
其中,是第n次循环中第j层物面的振幅,为第n次循环中第j层物面的相位.用原始物体的第j层物面的振幅aj替换得到调制后的第n次循环中第j层物面的复振幅:

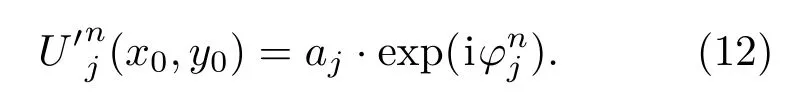
最后,每层物面再通过平面波角谱衍射传到全息面并叠加,得到第n+1次循环中的全息图,其复振幅表示为

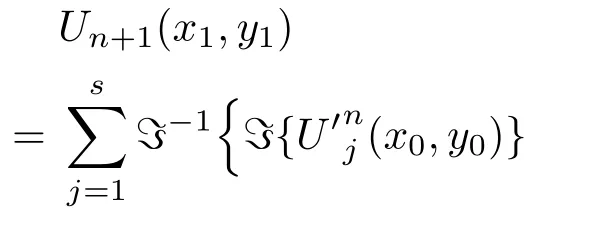
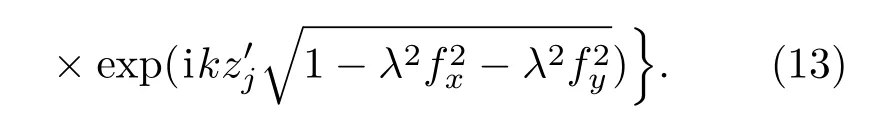
当n=N时终止循环,N为迭代次数.

将三维火车头通过计算机渲染技术得到强度图和深度图,如图8(a)和图8(b)所示.

基于图8(a)和图8(b),首先将三维火车头的强度图分解为R,G,B三基色图,如图9(a)—(c)所示.

然后,分别用传统的分层角谱算法和基于分层角谱的GS算法计算三维火车头的三基色全息图,得到图10所示结果,其中基于分层角谱的GS算法迭代5000次.

根据图10所示的全息图分别重建三维火车头,结果如图11所示.

图8 三维火车头 (a)强度图;(b)深度图Fig.8.Three-dimensional locomotive:(a)Intensity map;(b)depth map.

图9 火车头的三基色图 (a)R基色图;(b)G基色图;(c)B基色图Fig.9.Three color images of three-dimensional locomotive:(a)R-based color map;(b)G-based color map;(c)B-based color map.

图10 采用两种算法计算火车头的三基色图对应的全息图 (a)R通道全息图(传统的分层角谱算法);(b)G通道全息图(传统的分层角谱算法);(c)B通道全息图(传统的分层角谱算法);(d)R通道全息图(基于分层角谱算法的GS算法);(e)G通道全息图(基于分层角谱算法的GS算法);(f)B通道全息图(基于分层角谱算法的GS算法)Fig.10.Corresponding holograms of three color images of tea set:(a)R-channel hologram(traditional angularspectrum layer-oriented);(b)G-channel hologram(traditional angular-spectrum layer-oriented);(c)B-channel hologram(traditional angular-spectrum layer-oriented);(d)R-channel hologram(the GS algorithm based on angularspectrum layer-oriented method,iteration 5000 times);(e)G-channel hologram(the GS algorithm based on angularspectrum layer-oriented method,iteration 5000 times);(f)B-channel hologram(the GS algorithm based on angularspectrum layer-oriented method,iteration 5000 times).

图11 传统分层角谱算法与基于分层角谱的GS算法的再现像的比较 (a)在180 mm处再现像(分层角谱);(b)在180 mm处再现像(基于分层角谱的GS算法);(c)在210 mm处再现像(分层角谱);(d)在210 mm处再现像(基于分层角谱的GS算法);(e)在240 mm处再现像(分层角谱);(f)在240 mm处再现像(基于分层角谱的GS算法)Fig.11.Comparison of reconstructive images between angular-spectrum layer-oriented method and the GS algorithm based on angular-spectrum layer-oriented method:(a)The reconstruction of image at 180 mm(angularspectrum layer-oriented);(b)the reconstructionof image at 180 mm(the GS algorithm based on angular-spectrum layer-oriented method);(c)the reconstruction of image at 210 mm(angular-spectrum layer-oriented);(d)the reconstruction of image at 210 mm(the GS algorithm based on angular-spectrum layer-oriented method);(e)the reconstruction of image at 240 mm(angular-spectrum layer-oriented);(f)the reconstruction of image at 240 mm(the GS algorithm based on angular-spectrum layer-oriented method).

从图11(a)与图11(b)、图11(c)与图11(d)、图11(e)与图11(f)之间的比较可以看出,传统的分层角谱算法和基于分层角谱的GS算法计算得到的再现像较之原物体都存在一定的颜色失真,但传统的分层角谱算法计算得到的再现像,其背景及物体本身的散斑噪声较大,较为模糊;基于分层角谱的GS算法的再现像散斑噪声较少,更为清晰.为直观地证明两种算法再现像的差异,计算两种算法的RMSE和PSNR来进行质量评估,RMSE越小,再现像质量越好;PSNR越大,再现像质量越好.根据文献[16],RMSE的公式为

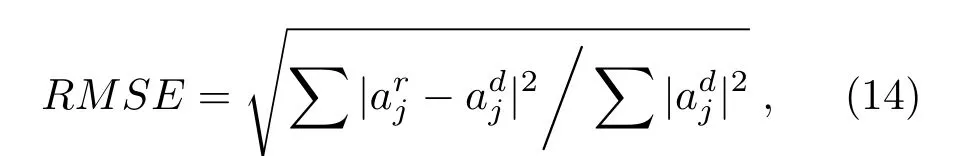
其中是第j层重建像的振幅分布,是第j层原始物体的振幅分布.根据文献[17],PSNR的公式为

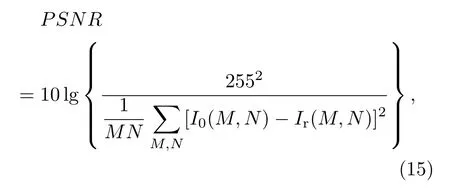
其中,M,N分别是水平和竖直方向的像素数;I0,Ir分别为原始图像和再现像的光强分布.绘制出RMSE和PSNR随着迭代次数的变化曲线,如图12所示.

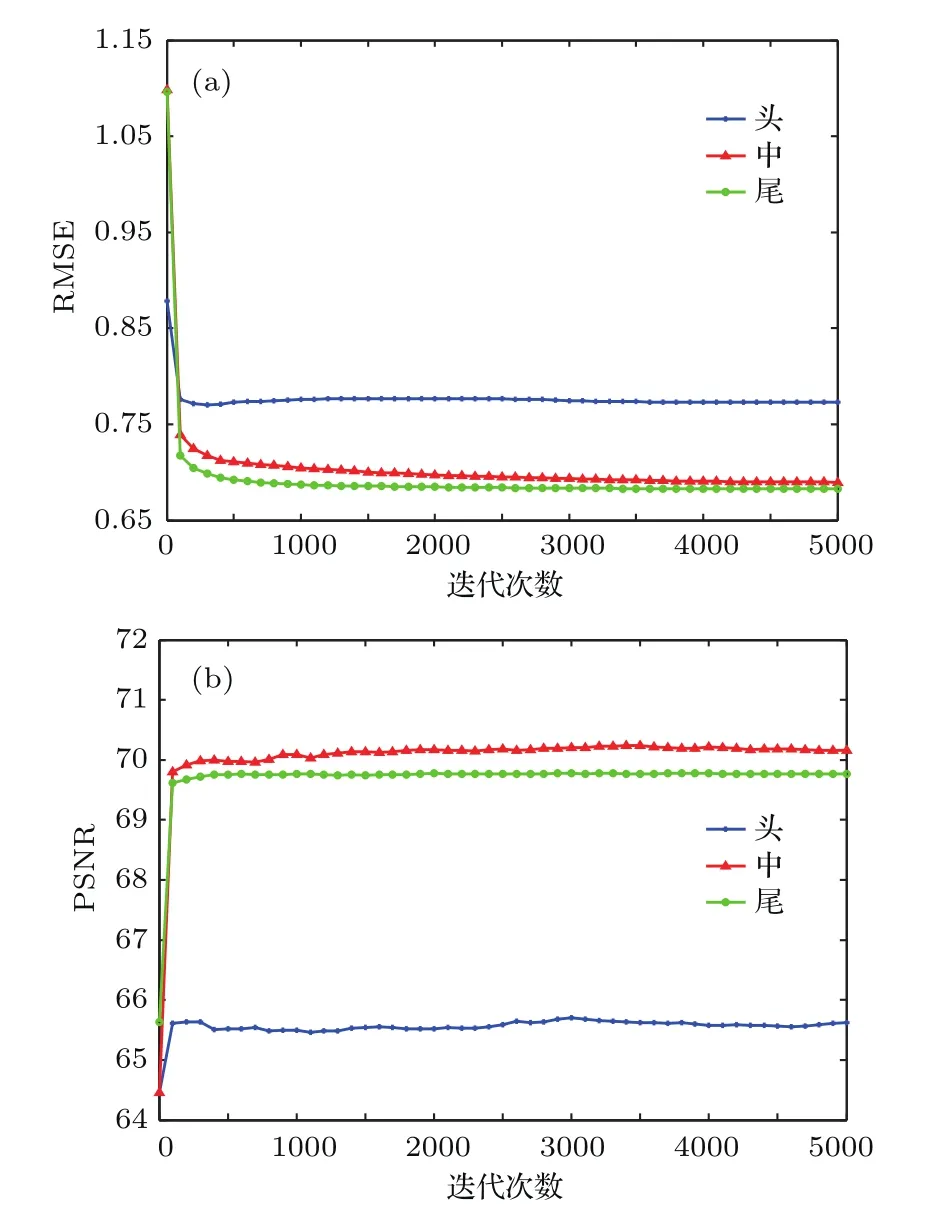
图12 分层角谱算法与基于分层角谱的GS算法的误差比较(a)RMSE;(b)PSNRFig.12.Error comparison between angular-spectrum layeroriented method and GS algorithm based on angularspectrum layer-oriented method:(a)RMSE;(b)PSNR.

在图12中,当迭代次数为0即未进行GS迭代时,RMSE和PSNR是利用传统的分层角谱算法计算得到的,当开始进行GS迭代时,利用基于分层角谱的GS算法计算再现像的RMSE和PSNR.在5000次迭代内RMSE和PSNR最终都趋近于收敛,且图12(a)中RMSE随着迭代次数的增加而减小,在前100次迭代内迅速减小,图12(b)中PSNR随着迭代次数的增加而增大,在前100次迭代内增加速度快,该结果证明了基于分层角谱的GS算法收敛速度快,再现像质量更好.但图12(a)中的RMSE和图12(b)中的PSNR在某个几百次迭代内均有小的起伏,RMSE的起伏范围是±0.02,PSNR的起伏范围±0.08,这是GS算法的局部收敛特性引起.基于分层角谱的GS算法计算5000次迭代内火车头的再现像,其头部的RMSE近似收敛到0.77,PSNR近似收敛到65.7,火车头中部和尾部的RMSE近似收敛到0.68,PSNR近似收敛到70.0,即火车头头部再现像质量明显低于中部和尾部;同传统分层角谱算法的再现像相比,其再现像的头部、中部和尾部的RMSE分别减小了约0.11,0.40和0.41,PSNR分别增大了约1.15,5.70和4.13,证明了基于分层角谱的GS算法可以对细节信息多的复杂物体进行高质量地重建,有效地抑制散斑噪声.

本文提出的基于分层角谱的GS算法的模型结合了分层角谱算法和GS算法的优点.算法的复杂度只与分层层数相关,与物体的复杂程度无关,可以进行复杂三维形貌物体的计算;避免了傍轴近似带来的计算误差;且收敛速度快,有效地抑制散斑噪声,提高成像质量.

4 结 论

本文分析了分层角谱算法在计算真彩色物体全息图时的多波长采样问题,并分别采用分层角谱算法和基于分层角谱的GS算法计算真彩色物体的全息图和再现像.通过计算RMSE和PSNR评估再现像的质量,验证本文提出的基于分层角谱的GS算法可有效地抑制散斑噪声,提高再现像质量.在本文算法中,迭代次数越多,成像质量越好,散斑越少,但计算时间增加.所以,在实际高精度的全息计算过程中,可采用GPU等硬件[27−29],并行处理模式、大量的线程运算等结合[30,31]的方法,进行高速计算全息图并高质量成像.

本文研究工作承蒙美国弗吉尼亚理工暨州立大学(Virginia Tech)Ting-Chung Poon教授指导修改完成,谨致谢意！同时,研究工作得到安徽大学韦穗教授的指点和帮助,在此一并表示感谢!

参考文献

[1]Goodman J W,Lawrence R W 1967Appl.Phys.Lett.11 77

[2]Adam K,David L K 1965Appl.Opt.4 387

[3]Qian X F 2015Information Optical Digital Laboratory(Beijing:Science Press)p200(in Chinese)[钱晓凡 2015信息光学数字实验室(北京:科学出版社)第200页]

[4]Gabor D 1948Nature161 777

[5]Leith E N,Upatnieks J 1963J.Opt.Soc.Am.53 1377

[6]Tan F 2012Opt.Instrum.34 16(in Chinese)[覃芳 2012光学仪器34 16]

[7]Waters J P 1966Appl.Phys.Lett.9 405

[8]Matsushima K,Nakahara S 2009Appl.Opt.48 H54

[9]Pan Y J,Wang Y T,Liu J,Li X,Jia J 2014Appl.Opt.53 1354

[10]Sun P,Xie J H,Zhou Y L 2004Acta Opt.Sin.24 110(in Chinese)[孙萍,谢敬辉,周元林2004光学学报24 110]

[11]Li J C 2014Di ff raction Calculations and Digital Holography(Vol.1)(Beijing:Science Press)p261(in Chinese)[李俊昌2014衍射计算及数字全息(上册)(北京:科学出版社)第261页]

[12]Poon T C,Liu J P 2014Introduction to Modern Digital Holography with MATLAB(London:Cambridge University Press)p5

[13]Michal M,Maciei S,Andrzei K,Grzegorz M 2005Opt.Eng.44 125805

[14]Cao X M,Sang X Z,Chen Z D,Leng J M,Zhang M,Guo N,Yu C X,Xu D X 2014Chin.J.Lasers41 0609002(in Chinese)[曹雪梅,桑新柱,陈志东,冷俊敏,张明,郭南,余重秀,徐大雄2014中国激光41 0609002]

[15]Chang C L,Xia J,Yang L,Lei W,Yang Z M,Chen J H 2015Appl.Opt.54 6994

[16]Pang H,Wang J Z,Cao A X,Zhang M,Shi L F,Deng Q L 2017IEEE Photon.J.9 1

[17]Zhao Y,Cao L C,Zhang H,Kong D Z,Jin G F 2015Opt.Express23 25440

[18]Gerchberg R W,Saxton W O 1972Optik35 237

[19]Xie J H,Liao N F,Cao L C 2007Fundamentals of Fourier Optics and Contemporary Optics(Beijing:Beijing Polytechnic University Press)p79(in Chinese)[谢景辉,廖宁放,曹良才2007傅里叶光学与现代光学基础(北京:北京理工大学出版社)第79页]

[20]Shen C,Wei S,Liu K F,Zhang F,Li H,Wang Y 2014Laser Optoelectr.Prog.51 030005(in Chinese)[沈川,韦穗,刘凯峰,张芬,李浩,王岳2014激光与光电子学进展51 030005]

[21]Piao Y L,Kwon K C,Jeong J S,Kim N 20163D Image Acquisition and Display:Technology,Perception and ApplicationsHeidelberg,Germany,July 25–28,2016 JW4A.29

[22]Peng J M,Du S J,Jiang P Z 2013High Power Laser and Particle Beams25 315(in Chinese)[彭金锰,杜少军,蒋鹏志2013强激光与粒子束25 315]

[23]Gu X,Xu K S 2000J.Fudan Univ.(Natural Science)39 205(in Chinese)[顾翔,徐克璹2000复旦学报(自然科学版)39 205]

[24]Wang J Y,Cao J H 2015J.Tianjin Univ.Technol.Education25 36(in Chinese)[王金洋,曹继华2015天津职业技术师范大学学报25 36]

[25]Li F,Bi Y,Wang H,Sun M Y,Kong X X 2012Chin.J.Lasers39 1009001

[26]Zhou P H,Bi Y,Sun M Y,Wang H,Li F,Qi Y 2014Appl.Opt.53 G209

[27]Pan Y C,Xu X W,Liang X N 2013Appl.Opt.52 6562

[28]Liu J,Ma X,Wang Y T,Jia J,Zhang Y X 2015 CN104281490A(in Chinese)[刘娟,马晓,王涌天,贾甲,张迎曦2015 CN104281490A]

[29]Kwon M W,Kim S C,Yoon S E,Kim E S 2015Opt.Express23 2101

[30]Chen H R,Fu S H,Wang Y Q 2014Opto-Electron.Eng.41 48(in Chinese)[陈慧荣,付胜豪,王元庆2014光电工程41 48]

[31]Fu S H,Wang Y Q,Bao X L,Fan K F 2013Electron.Opt.Control20 61(in Chinese)[付胜豪,王元庆,鲍绪良,范科峰2013电光与控制20 61]