超形变核态的相对论对称性研究

孙 铭，李冬鹏,2，陈寿万，郭建友*

(1.安徽大学 物理与材料科学学院，安徽 合肥230039； 2.合肥师范学院 电子信息工程学院，安徽 合肥230601)

对称性在原子核的壳层结构及其演化规律中扮演重要角色.自旋轨道相互作用的引进，成功地解释了实验室发现的幻数[1-2].赝自旋对称概念[3-4]解释了大量的核物理现象，包括原子核的超形变带、全同带、赝自旋伙伴带和幻数移动等.

为了揭示自旋和赝自旋对称性的起源，物理学家们做了大量工作.1949年，Jensen，Mayer等在Schrödinger方程中引入自旋-轨道相互作用，成功地解释了自旋对称性破缺[1-2].1969年，Arima，Hecht等发现单粒子态(n,l,j=l+1/2)和(n-1,l+2,j=l+3/2)的能量非常接近，具有近简并结构[3-4].赝自旋对称性被提出后，其起源问题一直没有弄清楚.Bahri等发现：当自旋-轨道耦合强度和轨道-轨道耦合强度满足一定比例时，原子核的赝自旋双重态近似简并，具有赝自旋对称性，并指出这一比例关系可由相对论平均场(relativistic mean field,简称RMF)理论解释[5].1997年，Ginocchio求解了球形核的Dirac方程，发现赝自旋对称性实质上是一种相对论对称性[6].严格赝自旋对称性的条件是Dirac方程中的标量势S和矢量势V之和为零，而且赝轨道角动量就是Dirac波函数下旋量中的轨道角动量，孟杰等将这一条件推广到更一般情况，即S+V=常数，并指出核中赝自旋对称性与赝离心势垒和赝自旋-轨道耦合势相关[7].文献[8]研究了反核子谱中的自旋对称性，发现反核子谱中的自旋对称性比核子谱中的赝自旋对称性保持得更好.

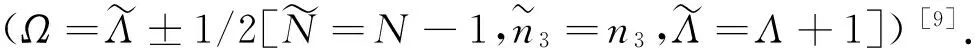
在原子核中，由于不存在非束缚核，严格的赝自旋对称性是不存在的.虽然人们对赝自旋对称性的起源进行了探讨，核中赝自旋对称性的破缺机制一直没有弄清楚.为此，郭建友课题组引入类重整化群(similarity renormalization group, 简称SRG)方法，通过连续幺正变换把Dirac哈密顿量转化成对角形式，探究相对论对称性,揭示相对论对称性的起源和破缺机制[17-18]；随后把这一方法推广到形变核，研究形变核的自旋和赝自旋对称性及其随形变演化的规律[19-20].该文利用相对论平均场理论研究超形变核态的相对论对称性.

1 理论框架

在相对论平均场理论[21]框架下，核子间通过交换介子发生相互作用，模型的拉格朗日密度可表达为

(1)

其中

Ωμν=∂μων-∂νωμ，

Rμν=∂μρν-∂νρμ-gρ(ρμ×ρν)，

Fμν=∂μAν-∂νAμ，

由欧拉-拉格朗日方程

(2)

导出的核子运动Dirac方程为

[α·p+V(r)+β(M+S(r))]ψ=εψ，

(3)

其中

S(r)=gσσ，

相对论平均场理论细节可参看文献[21]，在此不再赘述.

2 计算结果与讨论

以194Hg为例，研究超形变核态的相对论对称性，用相对论理论计算原子核的结合能、单粒子能级，相互作用参数组取NL3.图1展示了194Hg原子核的总结合能随形变变化的曲线，其中能量的最低点被设置为零.从图1可以看出，194Hg能量曲线存在1个最小和2个极小，第1个极小对应正常形变态，第2个极小对应超形变态.这个结果与实验上发现的194Hg存在正常形变态和超形变核态一致，表明用相对论平均场理论分析超形变核的对称性是合适的.

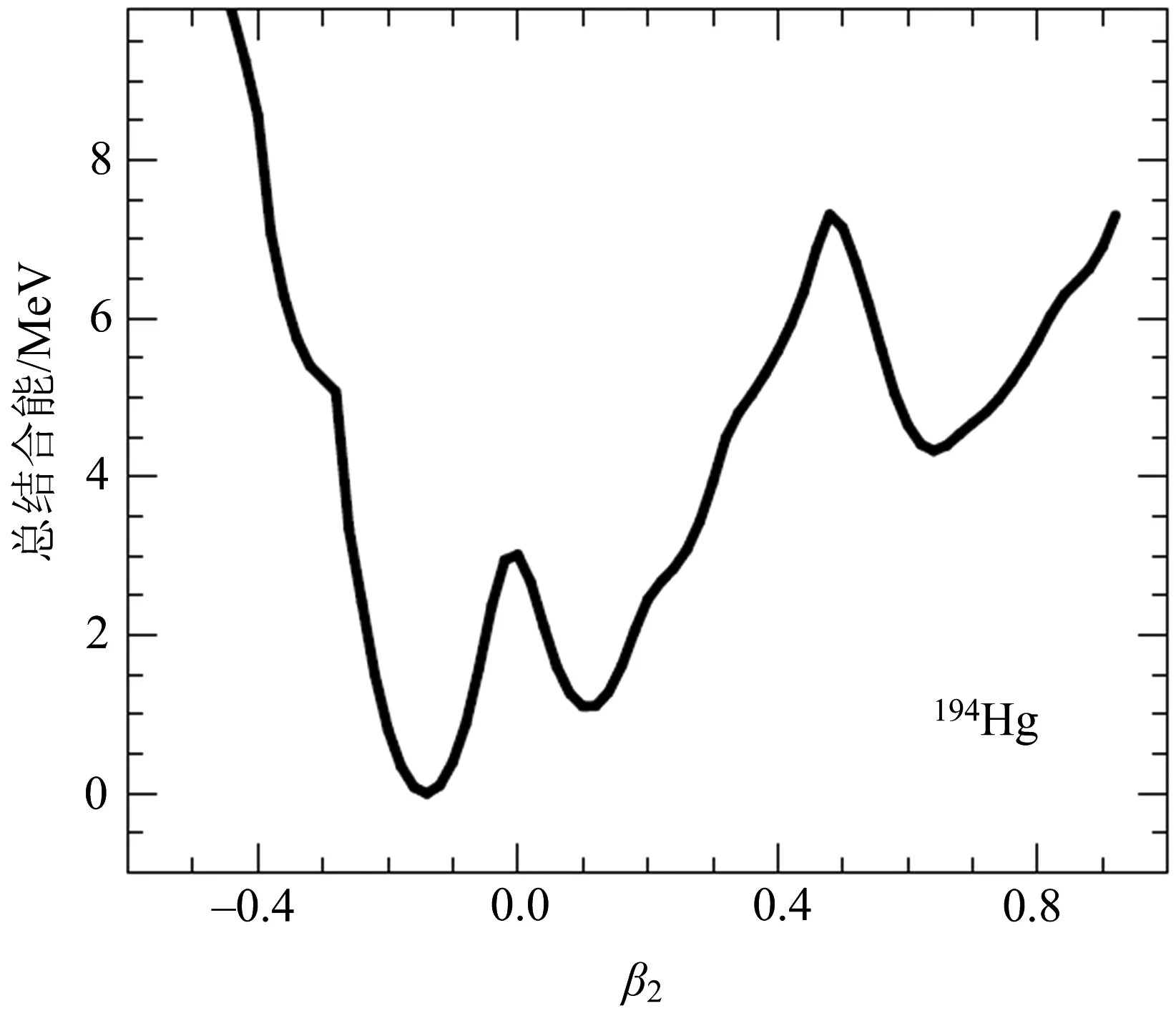
图1 原子核194Hg的总结合能随形变变化的曲线

图2展示了9对自旋双重态单粒子能级随形变的变化.左边是球形核单粒子态的标记，右边是形变核单粒子态的Nilsson标记.从图2中可以看出，自旋能量劈裂不仅与双重态的量子数相关，而且与原子核的形变相关.角动量第3分量最大的自旋双重态的单粒子能量随着形变的增加而减小，减小的程度随轨道量子数增加更加明显；角动量第3分量最小的自旋双重态的单粒子能量随着形变的增加而增加，增加的程度随轨道量子数增加更加突出；其他单粒子态的能量随形变变化的趋势介于上述两者之间.

图3展示了4个自旋双重态的自旋能量劈裂随形变变化的情况.从图3可以看出，球形核的自旋能量劈裂最大，随着形变的增加，自旋能量劈裂减小，减小的程度与双重态的量子数相关.在曲线的第2个极小(超形变核态处)，自旋能量劈裂最小或极小.随着形变的增加，自旋能量劈裂变化不大.当原子核处于超形变态时，不仅所有单粒子能量变小，而且自旋轨道劈裂变小，能级变密.这表明：超形变核态具有更好的自旋对称性，这也是超形变核态具有较好稳定性的原因之一.

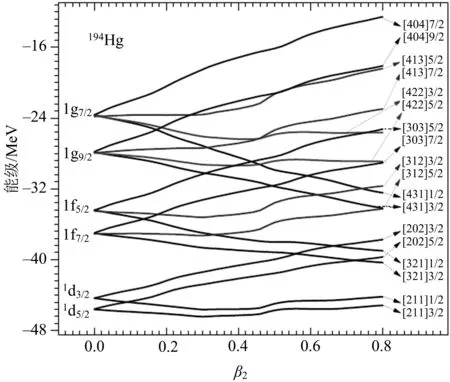
图2 自旋双重态单粒子能级随形变变化的情况

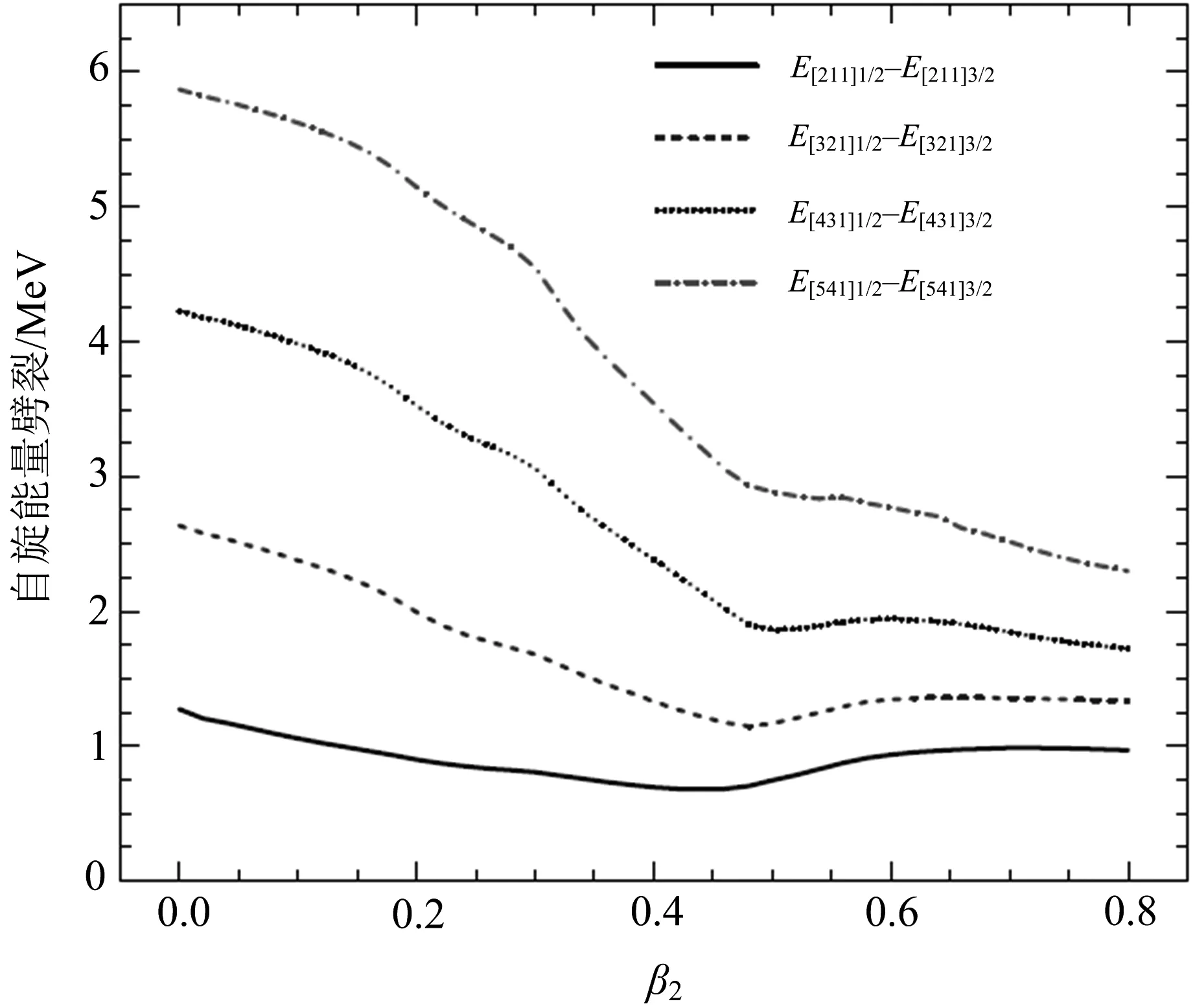
图3 自旋双重态的自旋能量劈裂随形变变化的情况

图4展示了从1g7/2和1g9/2自旋双重态分裂出的4个自旋双重态的自旋能量劈裂随形变变化的情况.从图4可以看出，随着形变的增加，自旋能量劈裂变化明显，双重态[431]1/2和[431]3/2的能量劈裂迅速减小，双重态[404]7/2和[404]9/2的能量劈裂迅速增加.形变β2>0.4时，随角动量第3分量的增加，自旋能量劈裂显著增加，即角动量第3分量小的双重态自旋对称性更好.遍及形变范围，双重态([431]1/2,[431]3/2)和([422]3/2,[422]5/2)的能量劈裂小于球形情况，在超形变处，几乎最小，这反映194Hg处于超形变核态时拥有较好的自旋对称性，稳定性更好.

除了自旋对称性，笔者也探索了194Hg超形变核态的赝自旋对称性.图5展示了赝自旋双重态单粒子能量随形变变化的情况，左边是球形核单粒子态的标记，右边是形变核单粒子态的Nilsson标记.从图5可以看出，从同一球形赝自旋双重态轨道分裂出的多个赝自旋双重态中，角动量第3分量最大的一对双重态的单粒子能量随形变增加而增加；角动量第3分量最小的一对双重态的单粒子能量随形变增加而减小；对介于两者之间的赝自旋双重态，单粒子能量随形变变化介于两者之间.同时，也观察到，随形变增加赝自旋双重态的单粒子能级间隙变小，赝自旋对称性变好，即形变核比球形核具有更好的赝自旋对称性，大形变核比小形变核有更好的赝自旋对称性.

图4 从1g7/2和1g9/2自旋双重态分裂出的4个自 旋双重态的自旋能量劈裂随形变变化的情况

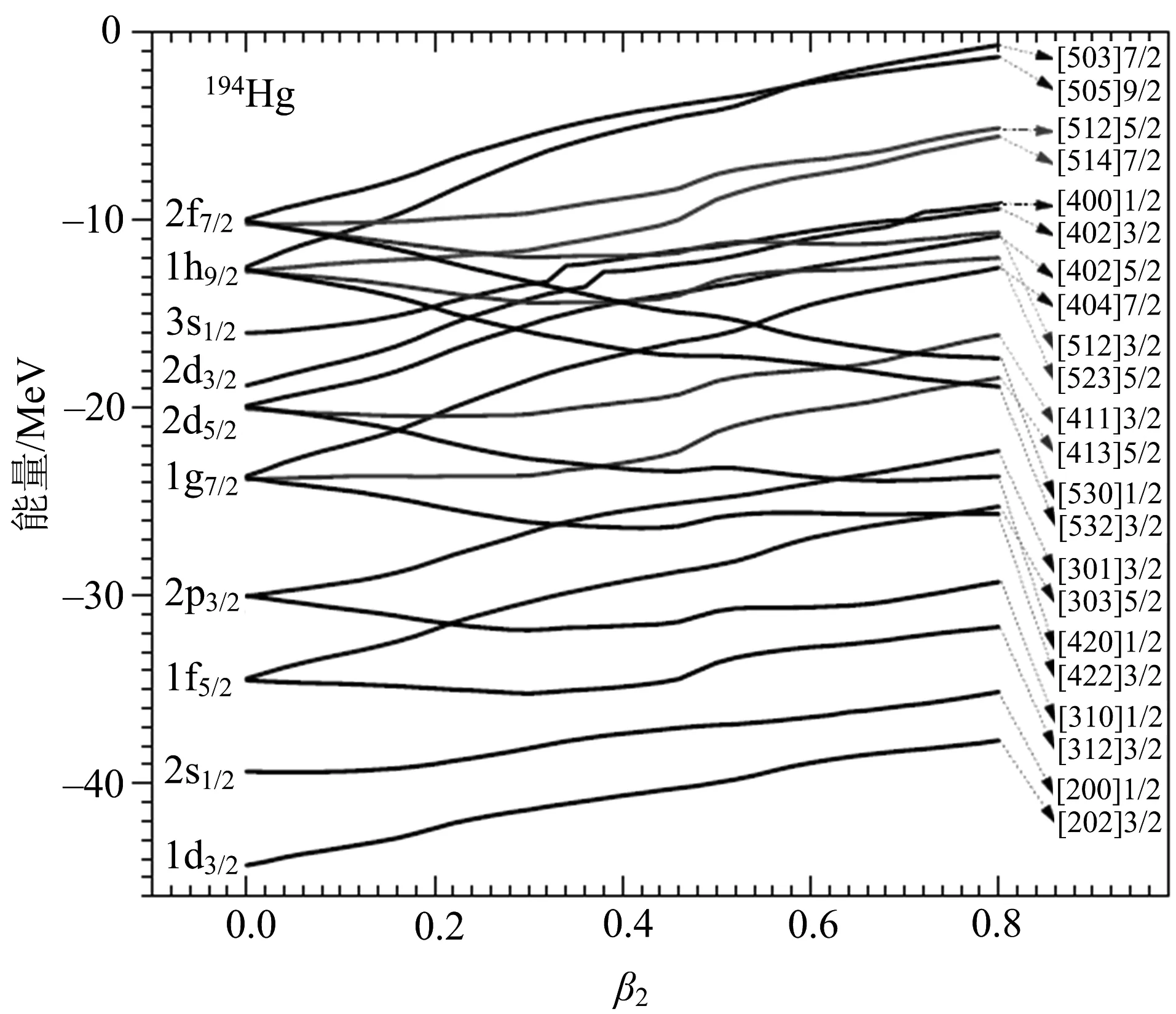
图5 赝自旋双重态单粒子能量随形变变化的情况

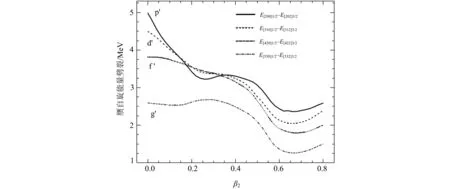
图6 赝自旋双重态的赝自旋能量劈裂随形变变化的情况

图7展示了同一球形赝自旋双重态分裂的4个赝自旋双重态的赝自旋能量劈裂随形变变化的情况.从图7可以看出，随着形变的增加，赝自旋双重态的赝自旋能量劈裂减小.随着角动量第3分量的增加，赝自旋双重态的赝自旋能量劈裂减小的速度更快.这些再次反映出，形变核具有更好的赝自旋对称性，大形变核的赝自旋对称性比小形变核的好.同时，也观察到，β2>0.6时，赝自旋双重态[503]7/2和[505]9/2的能量劈裂出现反转，但如此大的形变通常是不存在的.

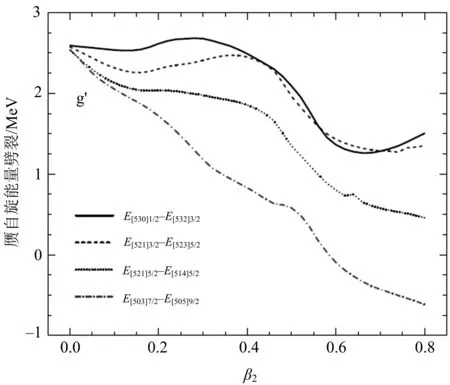
图7 同一球形赝自旋双重态分裂的4个赝自旋双重态的赝自旋能量劈裂随形变变化的情况

综上所述，形变核的单粒子能级结构及自旋和赝自旋对称性与能级的量子数和形变都相关.对于自旋对称性，随着形变的增加，自旋双重态的能量劈裂减小.当原子核处于超形变态时，不仅所有单粒子能量变小，而且自旋轨道劈裂变小，能级变密.对于赝自旋对称性，赝自旋能量劈裂与双重态的量子数和形变相关，形变核具有更好的赝自旋对称性，大形变核的赝自旋对称性比小形变核的好.

3 结束语

笔者利用相对论平均场理论计算了超形变核态的结合能和单粒子能级，提取了单粒子能级的自旋和赝自旋双重态的能量劈裂，研究了自旋和赝自旋对称性及其随形变变化的规律，结果表明：超形变核态的自旋和赝自旋对称性与双重态的量子数和形变都相关.对于自旋对称性，角动量第3分量大的自旋双重态，自旋能量劈裂随形变的增加而增加，角动量第3分量小的自旋双重态，自旋能量劈裂随形变的增加而减小.当原子核处于超形变态时，不仅所有单粒子能量变小，而且自旋能量劈裂出现最小或极小，能级变密，此表明超形变核态具有更好的自旋对称性.对于赝自旋对称性，赝自旋能量劈裂与双重态的量子数和形变都相关，形变核具有更好的赝自旋对称性，大形变核的赝自旋对称性比小形变核的好.

参考文献：

[1] HAXEL O , JENSEN J H D , SUESS H E. On the “magic numbers” in nuclear structure[J]. Phys Rev, 1949, 75: 1766.

[2] MAYER M G. On closed shells in nuclei[J]. Phys Rev, 1949, 75: 1969-1970.

[3] ARIMA A, HARVEY M, SHINIZU K. Pseudo LS coupling and pseudo SU (3) coupling schemes[J]. Phys Lett B, 1969, 30: 517-522

[4] HECHT K T, ADLER A. Generalized seniority for favoredJ≠ 0 pairs in mixed configurations[J]. Nucl Phys A, 1969, 137: 129-143.

[5] BAHRI C, DRAAYER J P, MOSZKOWSKI S A. Pseudospin symmetry in nuclear physics[J]. Phys Rev Lett, 1992, 68: 2133-2136.

[6] GINOCCHIO J N. Pseudospin as a relativistic symmetry[J]. Phys Rev Lett, 1997, 78: 436-439.

[7] MENG J, SUGAWARA-TANABE K, YAMAJI S, et al. Pseudospin symmetry in relativistic mean field theory[J]. Phys Rev C, 1998, 58: R628-R631.

[8] ZHOU S G, MENG J, RING P. Spin symmetry in the antinucleon spectrum[J]. Phys Rev Lett, 2003, 91: 262501.

[9] BOHR A, HAMAMOTO I, MOTTELSON B R. Pseudospin in rotating nuclear potentials[J]. Phys Scr, 1982, 26: 267-272.

[10] GAMBHIR Y K, MAHARANA J P, WARKE C S. Pseudo-spin as a relativistic symmetry[J]. Eur Phys J A, 1998, 3: 255-262.

[11] LALAZISSIS G A, GAMBHIR Y K, MAHARANA J P, et al. Relativistic mean field approach and the pseudospin symmetry[J]. Phys Rev C, 1998, 58: R45-R48.

[12] SUGAWARA-TANABE K, ARIMA A. Hidden pseudospin symmetry in the Dirac equation[J]. Phys Rev C, 1998, 58: R3065-R3068.

[13] SUGAWARA-TANABE K, YAMAJI S, ARIMA A. Pseudospin symmetry in the Dirac equation with a deformed potential[J]. Phys Rev C, 2000, 62: 054307.

[14] GINOCCHIO J N, LEVIATAN A, MENG J, et al. Test of pseudospin symmetry in deformed nuclei[J]. Phys Rev C, 2004, 69: 034303.

[15] GINOCCHIO J N. Relativistic symmetries in nuclei and hadrons[J]. Phys Rep, 2005, 414: 165-261.

[16] LIANG H Z, MENG J, ZHOU S G. Hidden pseudospin and spin symmetries and their origins in atomic nuclei[J], Phys Rep, 2015, 570: 1-84.

[17] GUO J Y. Exploration of relativistic symmetry by the similarity renormalization group[J]. Phys Rev C, 2012, 85: 021302 (R).

[18] LI D P, CHEN S W, GUO J Y. Further investigation of relativistic symmetry with the similarity renormalization group[J], Phys Rev C, 2013, 87: 044311.

[19] GUO J Y, CHEN S W, NIU Z M, et al. Probing the symmetries of the Dirac Hamiltonian with axially deformed scalar and vector potentials by similarity renormalization group[J]. Phys Rev Lett, 2014, 112: 062502.

[20] LI D P, CHEN S W, NIU Z M, et al. Further investigation of relativistic symmetry in deformed nuclei by similarity renormalization group[J]. Phys Rev C, 2015, 91: 024311.

[21] RING P. Relativistic mean field theory in finite nuclei[J]. Prog Part Nucl Phys, 1996, 37: 193-263.