有界量子等离子体中的孤波

陈建宏，常 博， 席盼祥，丁小婷

(兰州城市学院 电子与信息工程学院, 甘肃 兰州 730070)

由于量子等离子体在半导体材料[1]、高强度激光与等离子体相互作用[2-4]、高密度天体等离子体[5-6]等具有应用价值，故其已成为等离子体物理学中一个全新的、关注度高的研究对象.当等离子体中带电粒子的德布罗意波长与等离子体的空间尺度(如带电粒子的平均间距)可比较时，等离子体就会产生量子效应，其对应的等离子体被称为量子等离子体.Haas等[7]基于量子流体力学模型研究了量子等离子体中的离子声波.自此，从实验和理论方面，研究人员对线性与非线性量子等离子体波的性质进行了大量研究[8-12].然而，大部分研究工作没有考虑边界效应对量子等离子体波的影响.事实上，实验室中的量子等离子体通常具有明确的边界.已有研究表明，对没有考虑量子效应的等离子体系统，边界对等离子体波的性质也产生影响[13-15].不难想象，考虑边界效应后的量子等离子波将可能出现一些新的性质，笔者拟研究柱坐标系下有界量子等离子体系统.

1 动力学方程

所研究的量子等离子体系统由具有圆柱几何边界的电子与离子组成.等离子体满足如下连续性方程[7]

(1)

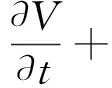
(2)

(3)

其中：ni为离子数密度；ne为电子数密度,ne服从玻尔兹曼分布，即ne=ne0exp(eφ/(kBTe))，kB和Te分别为玻尔兹曼常数和电子的温度；ν为运动黏滞系数；e为电子所带电量；V为量子等离子体的速率；φ为电位；mi为离子质量；ћ为约化普朗克常数;(2)式的第3项为考虑Bohm势而引入的量子项.

2 柱坐标系下拟KdV方程的导出

假设上述系统具有圆柱几何边界，速率V在柱坐标系下表示为Vr,Vθ,Vx.整个系统具有柱对称结构，即Vr=Vθ=0,Vx=V(x,r).系统径向尺寸r较小时，可假设∂V/∂r≪∂V/∂x，将方程(1)～(3)在柱坐标系下展开，并进行无量纲化，可得到如下无量纲方程

(4)

(5)

(6)

其中：无量纲的电子分布ne=exp(φ).

系统中的ni(r,x,t)，φi(r,x,t)，V(r,x,t)具有如下形式

ni(r,x,t)=Y0(r)Ni(x,t)+1，

(7)

φi(r,x,t)=Y0(r)ψ(x,t)，

(8)

Vi(r,x,t)=Y0(r)u(x,t).

(9)

(5)式中的量子项可表达为

(10)

利用泰勒公式将ni展开，保留低阶项后代入式(4)～(6)，可得

(11)

(12)

(13)

其中

β=3π/4R，ni=J0(βr)Ni(x,t)+1，V=J0(βr)u(x,t)，

令

ξ=ε(x-ct)，τ=ε3t，ν=ε3ν′.

采用约化摄动法,对式(11)～(13)中各物理量在平衡位置作如下展开

Ni=ε2N1+ε4N2+…，

(14)

u=ε2u1+ε4u2+…，

(15)

ψ=ε2ψ1+ε4ψ2+…,

(16)

其中:ε为无量纲小量,c为相速.

将式(11)～(13)的高阶近似方程联立后, 经过化简, 可得到如下形式的拟KdV方程

(17)

其中

3 孤立波特性分析

(1) 将β=3π/4R代入式(17)中,可得到D=9ν′π2/(32R2)，当D=0时，即ν′→0或者R→+时，式(17)将变成标准的KdV方程

(18)

方程(18)有如下形式孤立波解[16]

(19)

由式(19)可知，孤立波的波宽随着B变大而变大，也就是说加入量子项后孤立波的宽度变大.

(2) 当D≠0，令ψ1=6B1/3A-1ψ，τ=τ′，ξ=6B1/3ξ′，这样拟KdV方程(17)可改写为

(20)

方程(20)的解为

(21)

其中：a(τ′)=a0exp(-4Dτ′/3)为等离子体波的振幅，a0为初始条件下的振幅.此时，式(21)表示的是一种阻尼孤波，其振幅随时间衰减.当R减小时,D将变大，振幅将衰减变快，加入量子效应的衰减程度比不加入的小.

4 结束语

笔者研究了柱坐标系下有界量子等离子体系统，利用约化摄动法得到了描述该系统孤立波行为的拟KdV方程.研究发现：当边界参数R较小时，孤波振幅随时间衰减，且随着R的减小衰减变快；R趋近于+时，量子等离子体波呈现孤立波特性.

参考文献：

[1] XING L I, YAN Y. Large time behavior of solutions to 1-dimensional bipolar quantum hydrodynamic model for semiconductors[J]. Acta Mathematica Scientia, 2017, 37 (3): 806-835.

[2] HARVEY C N, GONOSKOV A, ILDERTON A, et al. Quantum quenching of radiation losses in short laser pulses[J]. Physical Review Letters, 2017, 118 (10): 105004.

[3] GLENZER S H, LANDEN O L, NEUMAYER P, et al. Observations of plasmons in warm dense matter[J]. Physical Review Letters, 2007, 98 (6): 065002.

[4] CROSS J E, REVILL B, GREGORI G. Scaling of magneto-quantum-radiative hydrodynamic equations: from laser-produced plasmas to astrophysics[J]. The Astrophysical Journal, 2014, 795: 59.

[5] OPHER M, SILVA L O, DAUGER D E, et al. Nuclear reaction rates and energy in stellar plasmas: the effect of highly damped modes[J]. Physics of Plasmas, 2001, 8 (5): 2454-2460.

[6] CHABRIER G, SAUMON D, POTEKHIN A Y. Dense plasmas in astrophysics: from giant planets to neutron stars[J]. Journal of Physics A: Mathematical and General, 2006, 39 (17): 4411.

[7] HAAS F, GARCIA L G, GOEDERT J, et al. Quantum ion-acoustic waves[J]. Physics of Plasmas, 2003, 10 (10): 3858-3866.

[8] SHUKLA P K, ELIASSON B. Nonlinear aspects of quantum plasma physics[J]. Physics-Uspekhi, 2010, 53 (1): 51-76.

[9] BRODIN G, MARKLUND M, MANFREDI G. Quantum plasma effects in the classical regime[J]. Physical Review Letters, 2008, 100 (17): 175001.

[10] TOLBA R E, EL-BEDWEHY N A, MOSLEM W M, et al. Nonlinear structures: cnoidal, soliton, and periodical waves in quantum semiconductor plasma[J]. Physics of Plasmas, 2016, 23 (1): 012111.

[11] BEHERY E E, HAAS F, KOURAKIS I. Weakly nonlinear ion-acoustic excitations in a relativistic model for dense quantum plasma[J]. Physical Review E, 2016, 93 (2): 023206.

[12] AGGARWAL M, KUMAR H, RICH A, et al. Self-focusing of Gaussian laser beam in weakly relativistic and ponderomotive cold quantum plasma[J]. Physics of Plasmas, 2017, 24 (1): 013108.

[13] WEI N X, XUE J K. Bounded dust-acoustic waves in a cylindrically bounded collisional dusty plasma with dust charge variation[J]. Physics of Plasmas, 2006, 13 (5): 052101.

[14] YANG X, LIU C B, YANG Y, et al. Existence and damping of dust acoustic solitary waves in a bounded geometry[J]. Physical Review E, 2013, 87 (6): 063101.

[15] LI G, REN Y Q. Damping solitary wave under the second and third boundary condition of a viscous plasma[J]. Indian Journal of Physics, 2017, 91 (2): 219-223.

[16] 刘式适，刘式达. 物理学中的非线性方程[M]. 北京：北京大学出版社，2000: 170-178.