改进的低纬度化极稳定算法

张 琪 张英堂 李志宁 范红波(陆军工程大学石家庄校区车辆与电气工程系,河北石家庄 050003； ②94019部队,新疆和田 848000)

1 引言

化极，即把观测到的磁力异常归算为假定磁源体位于地磁极处产生的磁力异常。频率域常规化极因子(Routine RTP Operator,RO)属于放大类因子，在低纬度地区，RO的幅值变得极大，导致化极极不稳定，会沿着地磁偏角方向产生严重的条带状异常。在噪声环境下，RO对高频成分的放大作用较强，导致化极结果的信噪比较低。因此，有必要研究快速、稳定的低纬度化极方法。

低纬度化极分为空间域方法和频率域方法。Baranov[1]首先提出化极的概念，并将空间域化极视为一种褶积运算；后来，空间域化极又被视为空间域反演问题[2,3]。空间域方法的优点是精度高，缺点是计算复杂且计算量大，涉及到大型线性方程组的求解问题。Bhattacharyya[4]利用傅里叶变换将空间域复杂的褶积运算转换成频率域简单的乘积运算，实现了频率域化极。频率域化极方法原理简单、计算快捷，已成为低纬度地区磁异常定性解释的有效手段[5]。根据压制区间的不同，可将频率域化极方法划分为两类： 一类主要用来压制不稳定的放大区，即磁偏角的垂直方向及其附近区域，称之为“局部压制类”化极方法； 另一类主要从全局进行压制，称之为“全局压制类”化极方法。

局部压制类化极方法主要对放大区内的RO进行改进，按改进方式的不同又可分为滤波法、阻尼法和分类讨论法等三种。

滤波法指在放大区将RO乘以一个特殊的滤波因子。姚长利等[6]利用一个余弦函数滤波因子定义压制因子(Suppression Filter,SF)，但压制边界角较难确定； Li[7]提出方位角滤波法(Azimuthal Filtering,AF)，其实质是给RO乘以一个正弦函数滤波因子。

阻尼法指在放大区将RO的分母加上一个较小的阻尼因子。姚长利等[8]定义了直接阻尼(Direct Damping,DD)法，并利用一个余弦阻尼因子压制不稳定的放大区； 林晓星等[9]通过增加相位因子和频率因子改进DD法，并将其定义为变频双向阻尼因子(Frequency Conversion Bidirectional Damping Factor，FC)法。

分类讨论法包括反对称因子(Antisymmetric Factor，ASF)法和非线性阈值法(Nonlinear Thresholding Method,NT)。Guo等[10]利用一个角度阈值将化极区域分成三个不同区域，在放大区内应用反对称因子(ASF)，在其他区域运用RO以保留有效的化极特征； Zhang等[11]把RO表示为复数形式，并用一个最优非线性幅度阈值分别稳定RO的实部和虚部。

全局压制类化极方法的基本原理是利用数学方程构造新的化极因子以稳定全部化极区域。Mendonça等[12]在向上延拓的基础上，推导了截断的泰勒级数法(Truncated Taylor Series Approximation Method,TT)，但该法的参数较难确定；双曲正弦函数法(Hyperbolic Sine Method,HS)[13]是将RO的分子和分母分别减去和加上一个改进的双曲正弦函数来稳定RO。

学者们针对低纬度化极做了深入研究，提出许多频率域化极方法，但仍存在以下问题： ①RO在垂直于地磁偏角方向极不稳定甚至奇异，导致化极结果出现严重的条带状干扰； ②局部压制类和全局压制类化极方法通过改进RO压制放大区，该过程不可避免地引入参数，并且参数的取值直接影响化极结果的精度，但针对参数取值的研究较少，往往都是利用经验值或给定参数范围； ③参数最优的RO在较低纬度仍表现出明显的高通滤波特性，对高频成分具有较强的放大作用，并且纬度越低，作用越明显。

针对以上问题，对RO进行改造，提出了局部压制类和全局压制类化极方法，然后通过计算化极结果与归一化磁源强度的最大相关系数得到了最优参数和最优参数下的化极结果，最后提出了正则化改进算法，得到了稳定的低纬度化极结果。

2 化极理论

2.1 频率域化极原理

频率域总场强度的RO可表示为

(1)

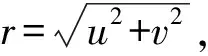
(2)

式中θ=arctan(v/u)。H(θ)依赖于I和D。在低纬度地区，I的值趋近于零，RO将变得不稳定。在极端情况下，即当θ=D±90°时，H(θ)的值趋近于无穷。设β为一小角度，则H(θ)在θ±β的区域内放大作用最强，称之为“放大区”。

2.2 局部压制类方法

滤波法的基本原理是在放大区将RO乘以一个滤波因子，在其他区域仍然使用RO，其原理表示为

(3)

式中：Hf(θ)表示滤波法的化极因子；Fβ(θ)表示滤波因子；α=θ-θ0,θ0=D±90°。

定义SF的余弦滤波因子和AF的正弦滤波因子分别为FSF(θ)和FAF(θ)，其表达式为

(4)

式中：Iac为低纬度特征角；p为压制衰减率。

阻尼法的实质是在放大区将RO的分母加上一个阻尼因子，其原理可表示为

Hd(θ)

(5)

式中：Hd(θ)表示阻尼法的化极因子；Fd(θ)表示阻尼因子。

用FDD(θ)和FFC(θ)分别表示DD法和FC法的阻尼因子，其表达式为

(6)

式中d、k和h分别表示阻尼因子、相位因子和频率因子。

用HASF(θ)表示ASF法的化极因子，其表达式为

(7)

式中θ′表示角度阈值。NT的基本原理可描述为

(8)

式中：x表示RO的虚部或实部；x′表示新的虚部或实部；θ1和θ2分别表示放大区的两个边缘角；Q表示非线性幅值阈值。

2.3 全局压制类方法

设HTT(θ)表示TT的化极因子，其定义为

HTT(θ)= {[sinI-icosIcos(θ-D)]×

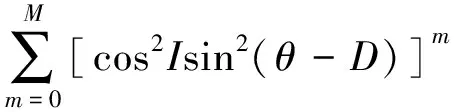
(9)

式中：M为一正整数，表示泰勒级数展开项的系数；K=2π|r|；l表示相对于观测面的延拓距离。

用HHS(θ)表示HS的化极因子，其表达式为

HHS(θ)=

(10)

式中：sinh表示双曲正弦函数；参数A的取值范围为2≤A≤12；参数B的取值范围为0.0001≤B≤0.1。

3 寻优

3.1 化极结果寻优

图1所示为频率域化极算法流程。根据图1可知，磁异常化极过程中，首先获得待测区域的磁异常信息，然后分别应用常规化极方法、局部压制类化极方法和全局压制类化极方法对总场数据进行化极，并利用相关系数法对化极因子的参数寻优，计算最优参数下的化极结果，并对化极效果进行评判。若化极结果能够准确、清晰地突出磁源体的磁异常特征，表明化极效果较理想，即可直接输出最优化极结果；若化极效果不理想，尤其当纬度很低且噪声很大时，参数最优的化极因子仍存在明显的高频放大效应，此时需对化极因子进行正则化改进，计算并输出正则化改进后的化极结果。

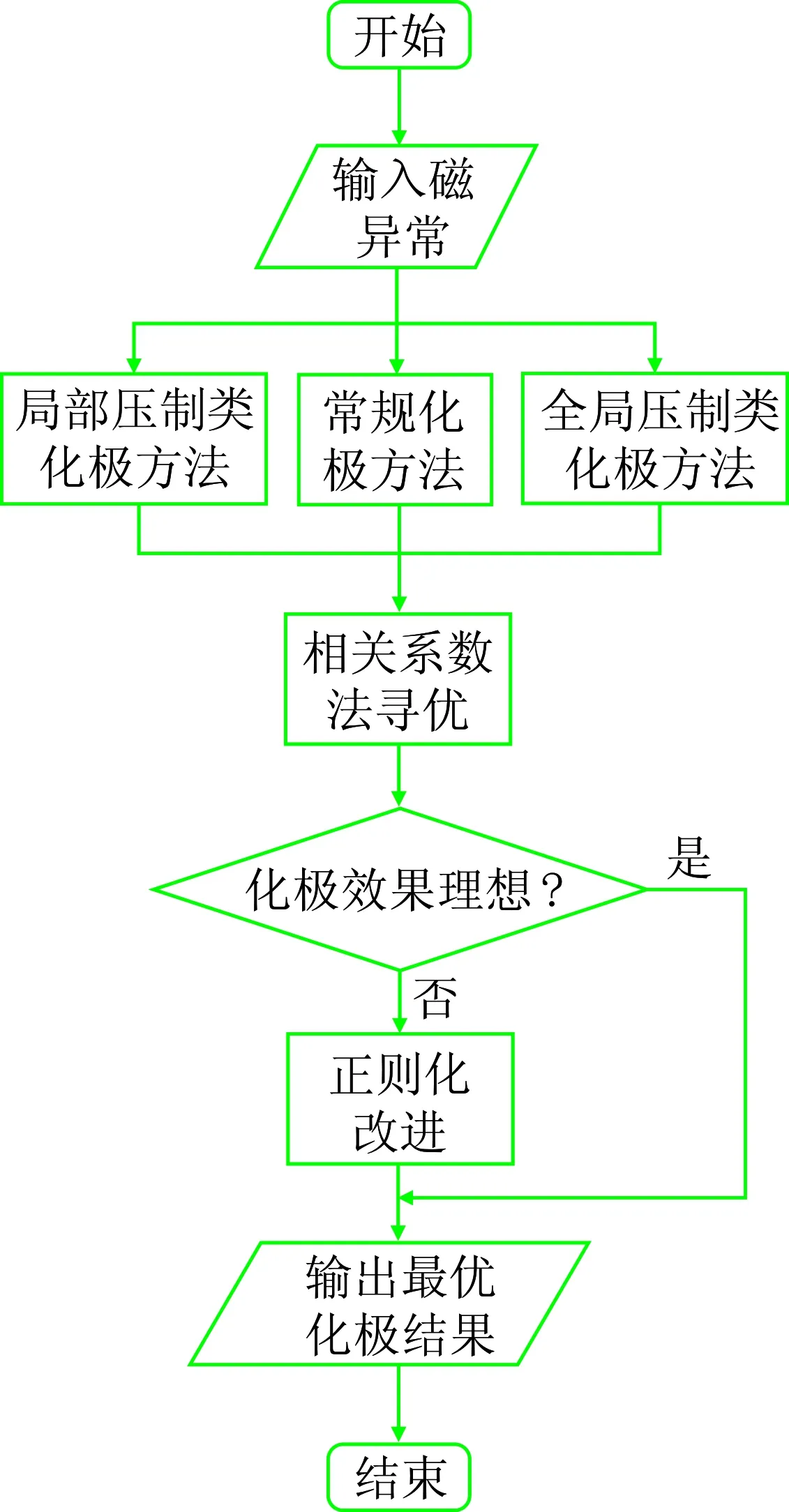
图1 化极算法流程

3.2 相关系数法

归一化磁源强度(Normalized Source Strength,NSS)是由磁偶极子的磁梯度张量的特征值矩阵推导出的一个旋转不变量[14,15]，NSS弱敏感于磁化方向，即使在低纬度地区，NSS仍能反映磁源体的磁性特征。

局部压制类和全局压制类化极方法可对不稳定的放大区进行有效压制，却不可避免地引入了参数，而参数取值直接影响化极结果的精度。因此，为了提高化极结果的精度，利用相关系数法对化极因子的参数寻优。相关系数可以描述化极结果与NSS的相关程度。相关系数越大，表明二者的对应关系越好，即最大相关系数对应最优参数。相关系数计算公式为

(11)

式中：X表示化极结果； cov(·，·)为协方差算子；D(·)为方差算子。

3.3 Tikhonov正则化

频率域化极可表示为

ST2(u,v)=H(u,v)ST1(u,v)

(12)

式中：ST1(u,v)表示斜磁化的总场数据的频谱；ST2(x,y)表示化极结果的频谱。

在低纬度地区，H(u,v)表现出明显的高通滤波特性。Zeng等[16]和Yin等[17]采用正则化滤波算子消除磁异常转换因子的噪声放大效应，有效提高了磁异常的信噪比。由于式(12)为病态问题，可将其转化为最小二乘形式[18,19]

min{‖H-1(u,v)ST2(u,v)-ST1(u,v)‖22+

λ‖ST2(u,v)‖22}

(13)

式中： ‖·‖22表示欧几里德范数的平方；λ为正则化参数。

求解式(13)可得

(14)

若Hλ(u,v)表示化极因子的正则化改进形式，可表示为

(15)

式(15)的极坐标形式可表示为

(16)

式中H′(θ)表示任意参数最优的化极因子。

采用L—曲线法[20]对λ进行参数寻优。L—曲线是一个方便的双对数图，在L—曲线的拐点处，即曲率最大的位置，对应最优λ，此时化极因子的压制效果最好。

3.4 均方根误差

为了衡量化极结果的精度，引入均方根误差(RMSE)作为定量评价指标，其定义为

(17)

式中：Nx和Ny分别表示x和y方向上的采样点总数；X⊥(i,j)表示垂直磁化条件下的理论磁异常值；X(i,j)表示化极磁异常值。

根据RMSE的定义，理论上，RMSE的值越小，则化极结果越接近于垂直磁化条件下的磁异常值，化极结果的精度越高；RMSE的值越大，表明化极结果的精度越低。

4 仿真试验

假设空间中存在如图2所示的由长方体、正方体和圆柱体组成的磁源体模型。长方体、正方体和圆柱体的中心坐标分别为(30m,-10m,16m)、(10m,30m,14m)和(-25m,-5m,18m)，长方体和正方体的边长分别为(20m,40m,20m)和(20m,20m,20m)，圆柱体的半径和母线长度分别为10m和50m。模型网格数为121×121，水平方向的采样间隔为1m。

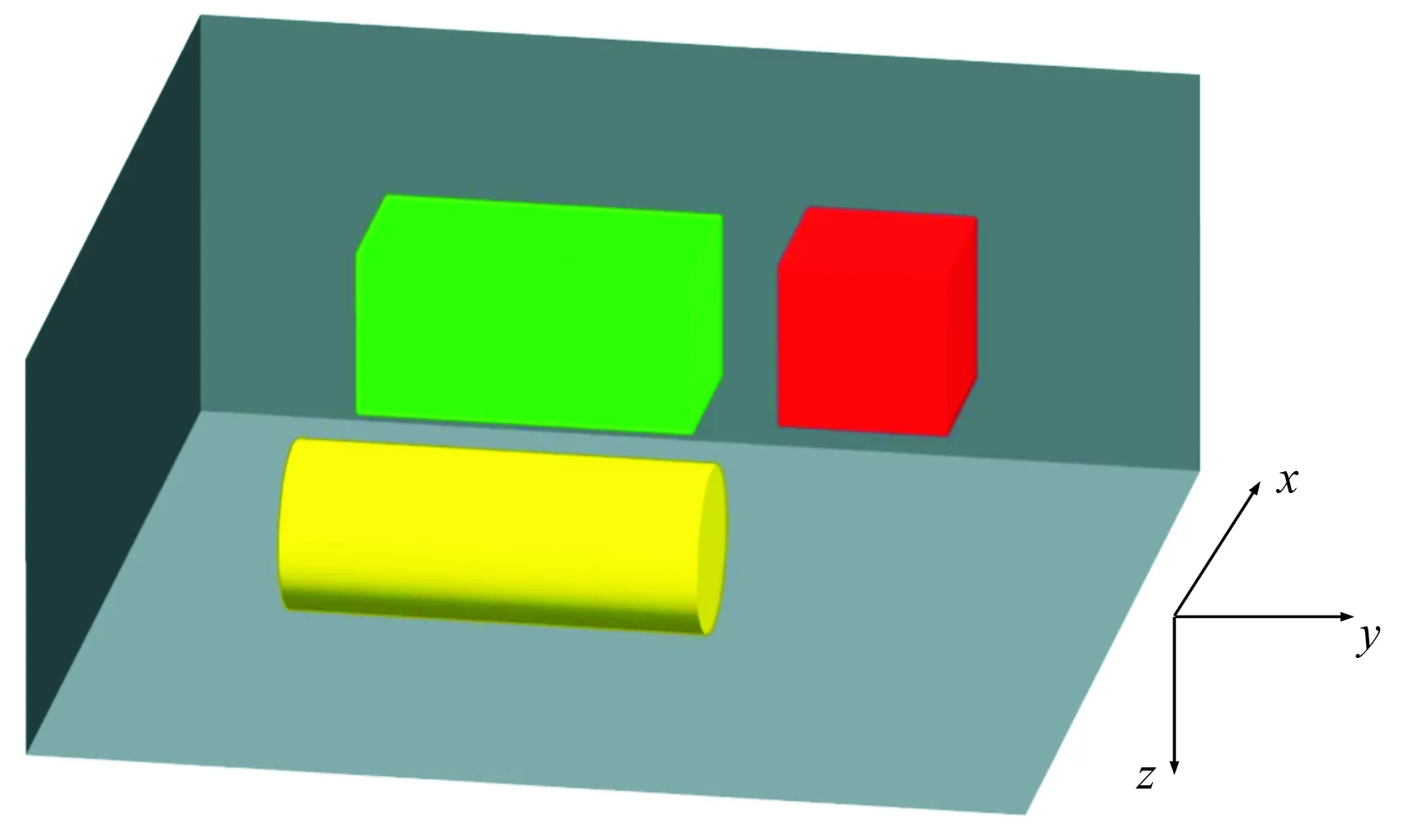
图2 组合体的空间位置示意图

由于地磁偏角仅起到图形旋转的作用，因此假设D=23°，组合体的磁化强度大小均为30A/m。对总场强度数据添加均值为0、方差为100nT的高斯白噪声，并且所有仿真均在该噪声环境下进行。需要说明的是，仿真中的地磁倾角、地磁偏角、磁化强度和噪声大小等参数均为任意取值，也可以选择其他数值验证所述方法的正确性。

当I分别等于90°、10°和1°时，组合体在z=0平面的总场强度如图3所示。根据图3可知，垂直磁化条件下的磁异常(图3a)与组合体的水平位置的对应关系最佳，磁异常形态清晰，易于辨识。相比之下，受磁化方向的影响，低纬度地区的磁异常(图3b和图3c)形态较复杂，与组合体的对应关系较差，磁异常数据的解释较困难。因此，为了降低斜磁化的影响，有必要对低纬度磁异常数据进行化极。

当I=10°时，利用前述九种方法进行化极的结果如图4所示，其RMSE如表1所示。

由图4可知，常规化极结果(图4i)产生了较多的沿着地磁偏角方向的条带状异常，化极效果不理想。相比之下，局部压制类和全局压制类化极方法的化极结果(图4a～图4h)的条带状异常明显减少，磁异常形态较清晰，辨识度较高。由表1可知，与RO法相比，SF、DD、ASF、AF、FC、NT、TT和HS法结果的RMSE较小，表明局部压制类和全局压制类化极方法对放大区的压制效果较好，化极结果的精度较高。根据上述分析可知，当I=10°时，局部压制类和全局压制类化极方法的化极效果优于常规化极方法，基本达到低纬度化极的目的。

当I=1°时，九种不同方法的化极结果如图5所示，其RMSE如表2所示。

由图5可知，ASF(图5c)和常规化极(图5i)结果已被噪声完全掩盖，磁异常值被严重放大，磁异常形态难以辨识；SF(图5a)、DD(图5b)和FC(图5e)化极结果产生了大量沿地磁偏角方向的条带状干扰，辨识度较差；AF(图5d)和NT(图5f)的化极结果产生了较多的条带状异常；相比之下，TT(图5g)和HS(图5h)化极结果的条带状异常基本没有出现，磁异常形态较清晰。由表2可知，RO和ASF计算结果的RMSE非常大，表明这两种算法的化极结果精度最低、化极效果差；与RO和ASF相比，SF、DD、AF、FC、NT、TT和HS的RMSE较小，表明这七种方法的化极精度较高。根据上述分析，当I=1°时，全局压制类化极方法的整体化极效果要明显优于局部压制类方法和常规化极方法，全局压制类化极方法基本能够达到低纬度化极的目的。

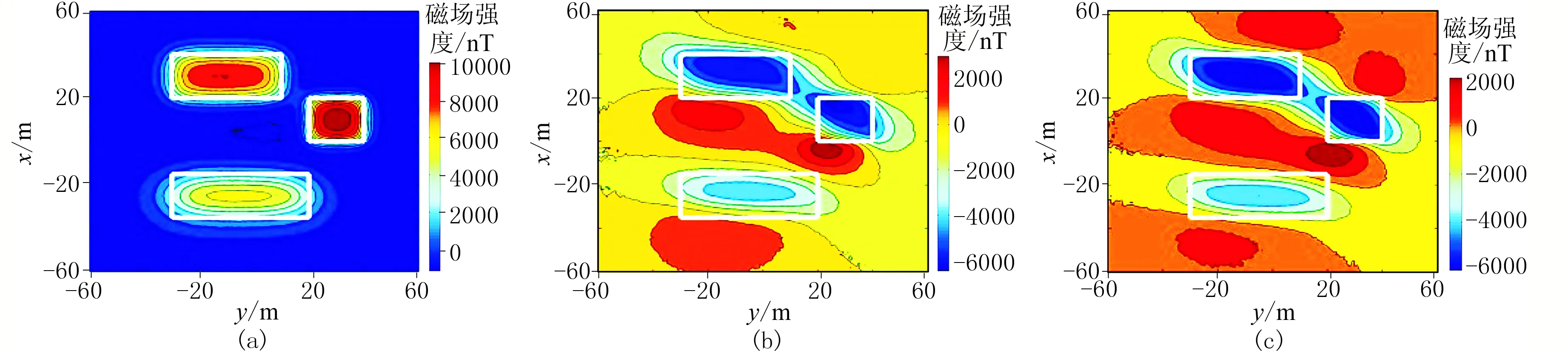
图3 组合体在不同地磁倾角时的总磁场强度分布图(z=0)(a)I=90°； (b)I=10°； (c)I=1°

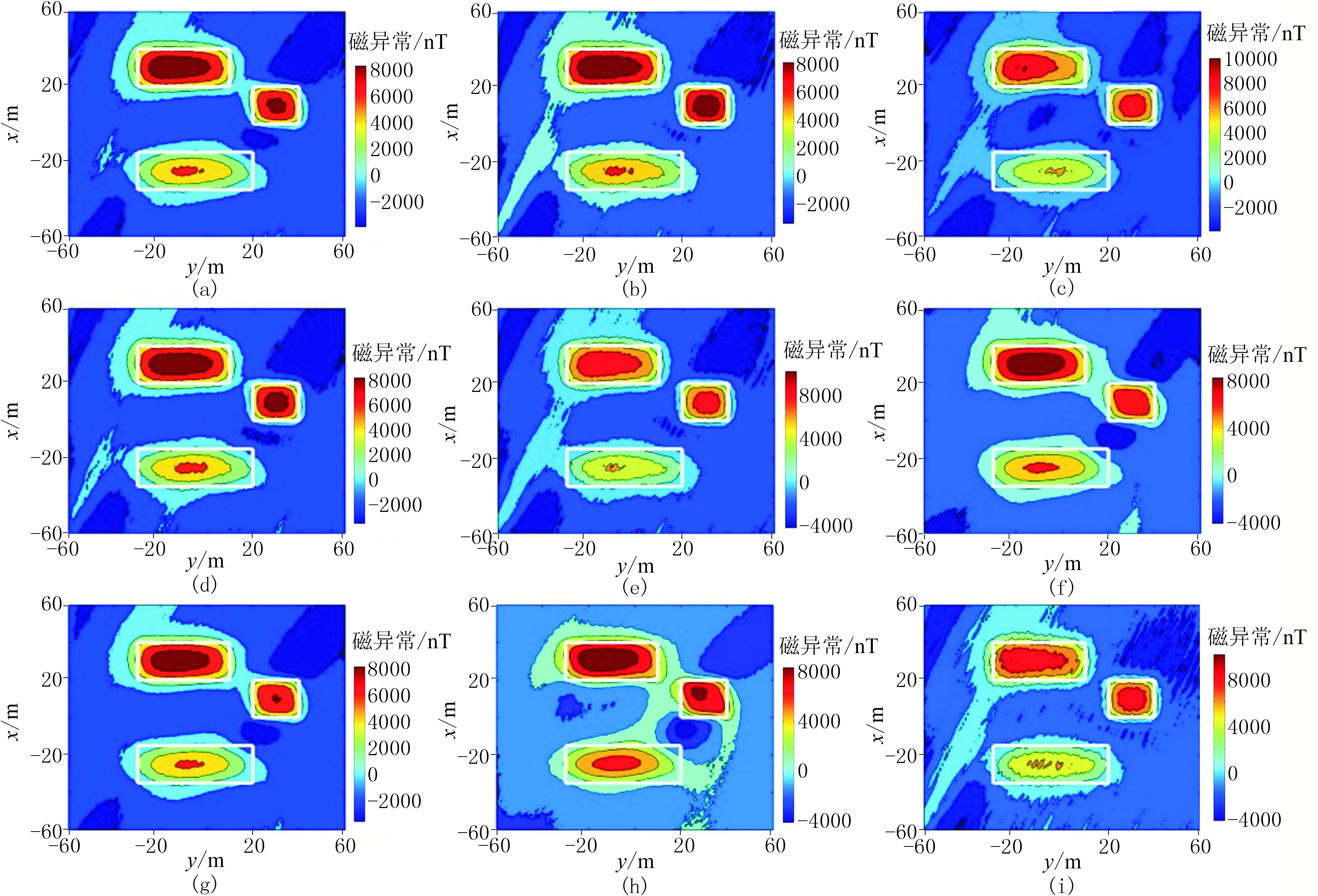
图4 九种方法在I=10°时的磁异常化极结果

(a)SF：β=20°，Corr=0.761； (b)DD：d=0.09，Corr=0.762； (c)ASF：θ′=64°，Corr=0.763； (d)AF：p=1，Corr=0.759； (e)FC：k=1，h=2，Corr=0.763； (f)NT：Q=15，Corr=0.759； (g)TT：M=20，Corr=0.755； (h)HS：A=5，B=0.001，Corr=0.718； (i)RO：Corr=0.756

表1 I=10°时九种方法磁异常化极结果的RMSE

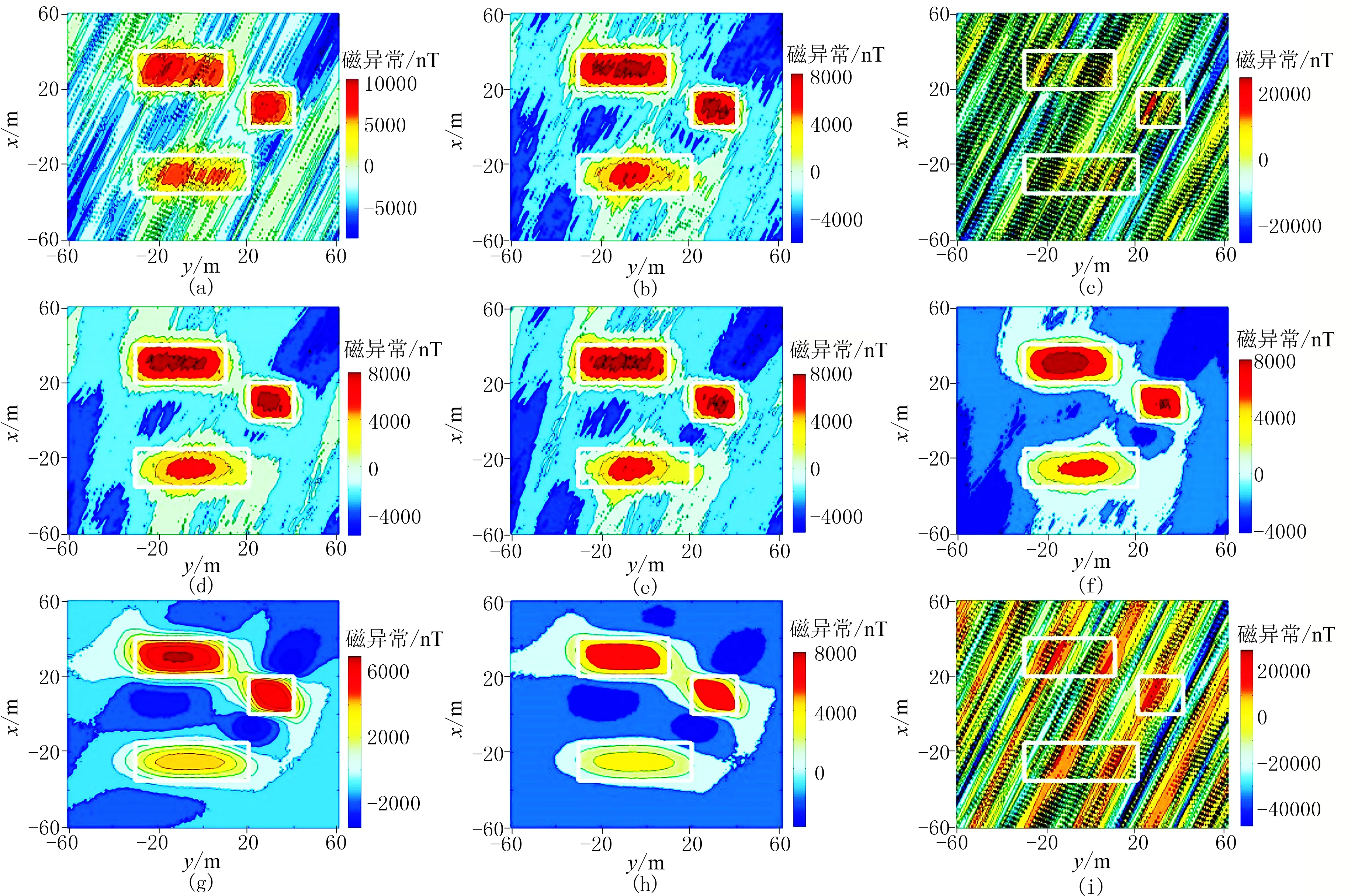
图5 九种方法在I=1°时的化极结果(a)SF：β=20°，Corr=0.649； (b)DD：d=0.5，Corr=0.72； (c)ASF：θ′=80°，Corr=0.216； (d)AF：p=5，Corr=0.736； (e)FC：k=2，h=2，Corr=0.735； (f)NT：Q=3，Corr=0.749； (g)TT：M1=20，Corr=0.755； (h)HS：A=12，B=0.03，Corr=0.745； (i)RO：Corr=0.131

表2 I=1°时九种方法的磁异常化极结果的RMSE

为了分析图5中九种化极结果存在明显差异的原因，分别绘制九种化极因子在I=1°时的幅频特性曲线(图6)。

由图6可知，当I=1°时，在不稳定区域化极因子幅值水平RO(图6i)最高，ASF(图6c)次之，然后依次是SF(图6a)、DD(图6b)、FC(图6e)、AF(图6d)、NT(图6f)，TT(图6g)和HS(图6h)最低。综合图5和图6可知，化极因子在不稳定区域内的幅值水平越低，化极因子对高频成分的压制作用越强，化极就越稳定。

当I=1°时，为了有效抑制化极因子的高频放大效应，利用式(16)对其进行正则化改进。正则化改进后的九种化极结果如图7所示，其RMSE统计结果如表3所示、幅频特性曲线如图8所示。

对比图7与图5可以看出，SF(图7a)、DD(图7b)、ASF(图7c)、AF(图7d)、FC(图7e)和常规化极结果(图7i)均得到明显改善，条带状异常基本消除，磁异常形态清晰、辨识度较高；NT(图7f)和HS(图7h)化极结果的分辨率更高；而TT(图7g)的化极结果无明显变化。

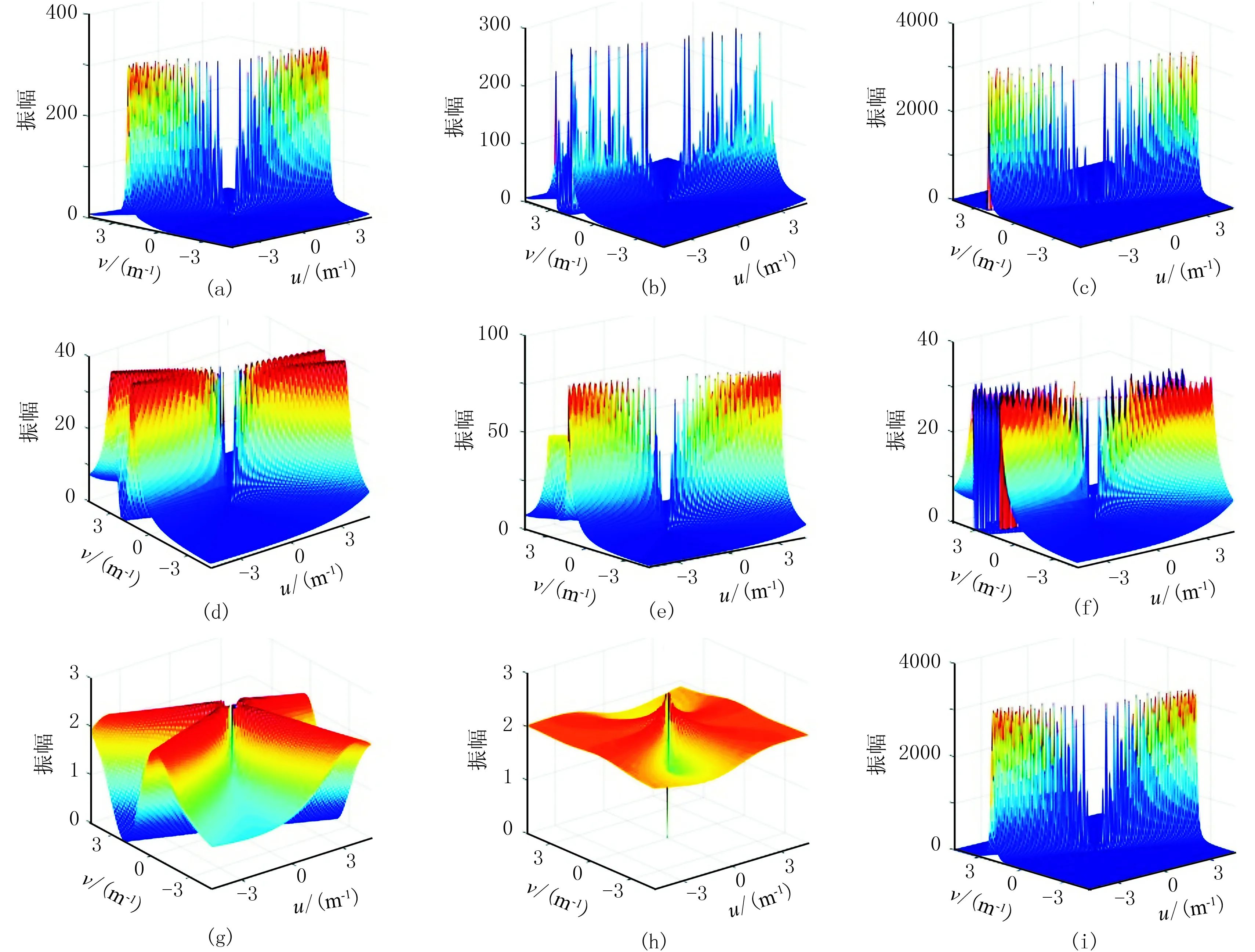
图6 I=1°时九种化极因子的幅频特性曲线(a)SF； (b)DD； (c)ASF； (d)AF； (e)FC； (f)NT； (g)TT； (h)HS； (i)RO

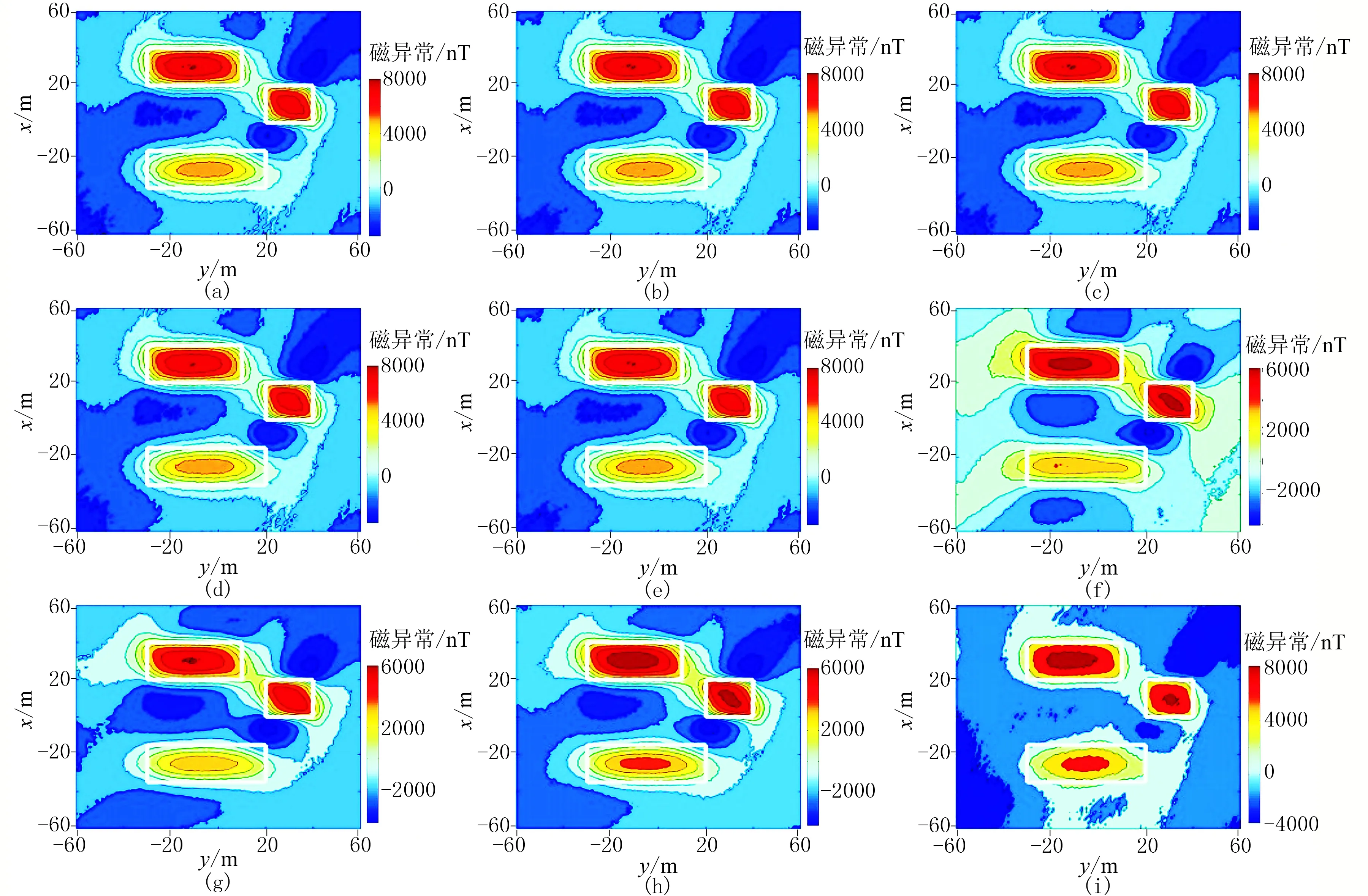
图7 正则化改进后九种方法在I=1°时的化极结果(a)SF； (b)DD； (c)AS； (d)AF； (e)FC； (f)NT； (g)TT； (h)HS； (i)RO

表3与表2相比，SF、DD、ASF、AF、FC、HS和RO的RMSE均明显变小，其中，RO和ASF的RMSE下降幅度较大；NT的RMSE增大，而TT的RMSE基本不变。上述分析表明，正则化改进后，SF、DD、AF、ASF、FC、HS和RO的化极精度得到明显提高。需要注意的是，NT的RMSE增大是由于正则化改进后的化极结果产生了一定的偏置，导致磁异常数值整体变小。由图7可知，NT(图7f)的化极结果能够清晰地反映出组合体的磁异常分布，化极效果较理想，基本达到化极的目的。

表3 I=1°时正则化改进后九种方法的磁异常化极结果的RMSE

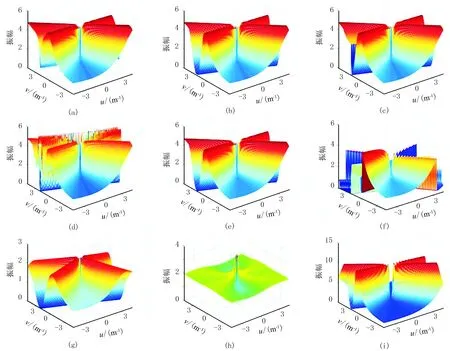
图8 I=1°时正则化改进后九种化极因子的幅频特性曲线(a)SF； (b)DD； (c)ASF； (d)AF； (e)FC； (f)NT； (g)TT； (h)HS； (i)RO

对比图8与图6可以看出，SF(图8a)、DD(图8b)、ASF(图8c)、AF(图8d)、FC(图8e)、NT(图8f)和RO(图8i)在不稳定区域内的幅值均明显降低，其中，ASF和RO的降低幅度较大；TT和HS无明显变化。上述幅值变化对应在图7中表现为化极结果的条带状异常得到消除，磁异常形态更加清晰。

根据上述分析可知，正则化改进算法通过降低化极因子在不稳定区域的幅值实现对高频成分的有效压制，表现为化极结果的条带状异常基本被消除，磁异常形态更清晰，化极更加稳定，化极结果的精度得到提高。

5 实验

为了验证改进化极算法的实际应用效果，对巴西中部的Goiás州北部某矿区的磁异常数据[11]进行处理。网格数为181×181，水平方向的采样间隔为250m。矿区的地磁倾角和地磁偏角分别为-5°和-15°，其实测总场强度如图9所示。

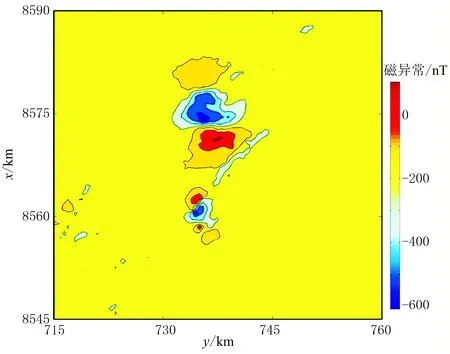
图9 巴西中部某矿区的实测磁异常分布图

由图9可知，实测磁异常不仅存在严重的噪声干扰，而且由于受到低纬度的影响，其磁异常形态十分复杂，磁异常值大多为负值，给该区域的磁异常数据解释带来了较大困难。

图10为最优参数下的九种方法化极结果。由图10可知，SF(图10a)、DD(图10b)、ASF(图10c)、AF(图10d)、FC(图10e)和常规化极结果(图10i)均被高频噪声完全掩盖，磁异常值被严重放大，并且产生了大量的条带状干扰，辨识度较差；NT(图10f)的化极结果产生了较多的条带状干扰，但尚能识别部分磁异常特征； 相比之下， TT(图10g)和HS(图10h)中的条带状异常较少，矿区的正负磁异常差异较明显，化极效果较为理想。

为了消除SF、DD、ASF、AF、FC、NT和RO这七种化极因子存在的高频放大效应，对其进行正则化改进，而不对TT和HS作任何处理。改进后的化极结果如图11所示，成图时采用相同的色标范围。其中TT(图11g)和HS(图11h)为最优参数下的化极结果，仅用于对比。对比图11与图10可以看出，SF(图11a)、DD(图11b)、ASF(图11c)、AF(图11d)、FC(图11e)和常规化极结果(图11i)均得到改善，条带状异常基本被消除，矿区的正负磁异常差异较明显；NT方法(图11f)的辨识度增强。整体来看，正则化改进后的七种化极结果、TT(图11g)以及HS(图11h)结果较为合理，矿区的化极磁异常特征较明显，已基本达到化极目的。

图10 实际数据九种不同方法的磁异常化极结果对比

(a)SF：β=20°，Corr=0.212； (b)DD：d=1，Corr=0.267； (c)ASF：θ′=71°，Corr=0.225； (d)AF：p=1，Corr=0.279； (e)FC：k=2，h=1，Corr=0.283； (f)NT：Q=1，Corr=0.318； (g)TT：M1=5，Corr=0.392； (h)HS：A=2，B=0.1，Corr=0.364； (i)RO：Corr=0.121

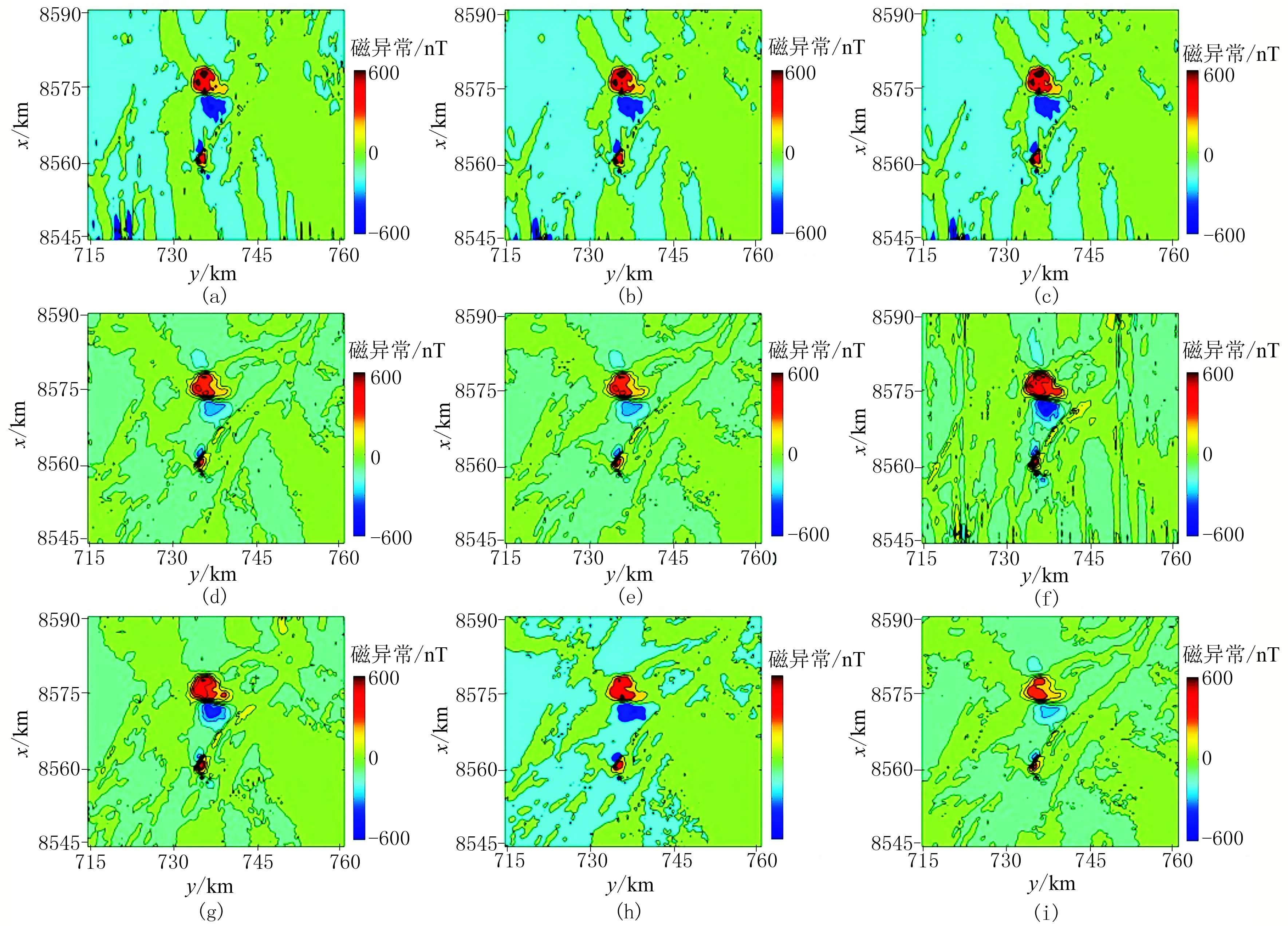
图11 实际数据正则化改进后磁异常化极结果对比(a)SF； (b)DD； (c)ASF； (d)AF； (e)FC； (f)NT； (g)TT； (h)HS； (i)RO

由于实际地磁环境十分复杂，且更容易受噪声的影响，因此实际数据处理的难度更大。应用改进的化极算法能够在一定程度上降低低纬度磁异常数据解释的难度，同时，九种不同化极方法能够在化极结果上互相验证，这也从另外一个角度证实了磁异常化极结果的可靠性。

6 结论

(1)基于对RO的改进，局部压制类和全局压制类化极方法能对不稳定的放大区进行高频压制，且全局压制类方法的压制效果要优于局部压制类方法。

(2)局部压制类和全局压制类化极方法在实现对放大区高频压制的同时也引入了参数，并且参数的取值直接影响化极结果的精度。通过计算化极结果与NSS的最大相关系数可以得到最优参数和最优参数下的化极结果，提高化极结果的精度。

(3)参数最优的化极因子在较低纬度仍存在高频放大效应，利用正则化改进算法能有效抑制原始信号中的高频噪声并提高化极结果的信噪比。

本文通过仿真试验和实际数据实验对比分析了九种化极方法的应用效果，并给出了相应的优化方法，最终得到了稳定的磁异常化极结果。在实际应用中，应根据纬度高低、噪声水平和实时化极效果等因素综合考虑，选取最优方法以获得最优化极结果。

值得注意的是，磁异常数据经过化极或化赤处理都能够降低斜磁化的复杂性。在低纬度地区，尤其是磁赤道处，化赤因子是稳定的。由于水平磁化的磁异常数据解释难度较大，因此也可以对低纬度磁异常数据进行化赤处理，然后倒相180°。

参考文献

[1] Baranov V.A new method for interpretation of aeromagnetic maps:pseudo-gravimetric anomalies.Geophysics,1957,22(2):359-382.

[2] Silva J B C.Reduction to the pole as an inverse pro-blem and its application to low-latitude anomalies.Geo-physics,1986,51(2):369-382.

[3] Leao J W D,Silva J B C.Discrete linear transformations of potential field data.Geophysics,1989,54(4):497-507.

[4] Bhattacharyya B K.Two-dimensional harmonic analysis as a tool for magnetic interpretation.Geophysics,1965,30(5):829-857.

[5] 柴玉璞.从化极算法误差方程看各种波数域低纬度化极方法.石油地球物理勘探,2012,47(3):496-505.

Chai Yupu.Discussion of wavenumber domain RTP methods at low latitudes.OGP,2012,47(3):496-505.

[6] 姚长利，管志宁，高德章等.低纬度磁异常化极方法——压制因子法.地球物理学报,2003,46(5):690-696.

Yao Changli,Guan Zhining,Gao Dezhang et al.Reduction to the pole of magnetic anomalies at low latitude with suppression filter.Chinese Journal of Geophysics,2003,46(5):690-696.

[7] Li X.Magnetic reduction-to-the-pole at low latitudes:Observations and considerations.The Leading Edge,2008,27(8):990-1002.

[8] 姚长利,黄卫宁,张聿文等.直接阻尼法低纬度磁异常化极技术.石油地球物理勘探,2004,39(5):600-606.

Yao Changli,Huang Weining,Zhang Yuwen et al.Reduction to the pole of magnetic anomalies at low latitude with direct damping.OGP,2004,39(5):600-606.

[9] 林晓星,王平.一种改进的低纬度磁场化极方法——变频双向阻尼因子法.地球物理学报,2012,55(10):3477-3484.

Lin Xiaoxing,Wang Ping.An improved method for reduction to the pole of magnetic field at low latitude -the method of frequency conversion bidirectional damping factor.Chinese Journal of Geophysics,2012,55(10):3477-3484.

[10] Guo L,Shi L,Meng X.The antisymmetric factor me-thod for magnetic reduction to the pole at low latitudes.Journal of Applied Geophysics,2013,92:103-109.

[11] Zhang H,Marangoni Y R,Hu X et al.NTRTP:A new reduction to the pole method at low latitudes via a nonlinear thresholding.Journal of Applied Geophy-sics,2014,111:220-227.

[12] Mendona C A,Silva J B C.A stable truncated series approximation of the reduction-to-the-pole operator.Geophysics,1993,58(8):1084-1090.

[13] 张培琴,赵群友.低磁纬度区航磁异常变倾角磁方向转换方法.物探化探计算技术,1996,18(3):206-214.

Zhang Peiqin,Zhao Qunyou.Methods of the magnetic direction transform of aeromagnetic anomalies with differential inclinations in low magnetic latitudes.Computing Techniques for Geophysical and Geoche-mical Exploration,1996,18(3):206-214.

[14] 张振宇,王刚,胡祥云等.张量CSAMT方法及对比实验.石油地球物理勘探,2017,52(4):869-874.

Zhang Zhenyu,Wang Gang,Hu Xiangyun et al.Tensor CSAMT technical and experiments.OGP,2017,52(4):869-874.

[15] Wilson H.Analysis of the magnetic gradient tensor.Defence Research Establishment Pacific:Canada Technical Memorandum,1985,85:13-47.

[16] Zeng X,Liu D,Li X et al.An improved regularized downward continuation of potential field data.Journal of Applied Geophysics,2014,106:114-118.

[17] Yin G,Zhang Y,Mi S et al.Calculation of the magne-tic gradient tensor from total magnetic anomaly field based on regularized method in frequency domain.Journal of Applied Geophysics,2016,134:44-54.

[18] 曹静杰.基于广义高斯分布和非Lp范数正则化的地震稀疏盲反褶积.石油地球物理勘探,2016,51(3):428-433.

Cao Jingjie.Seismic sparse blind deconvolution based on generalized Gaussian distribution and non-convex Lpnormal regularization.OGP,2016,51(3):428-433.

[19] 杨国权,丁鹏程,李振春等.应用线性程函方程和整形正则化的三维初至波旅行时层析.石油地球物理勘探,2017,52(2):264-272.

Yang Guoquan,Ding Pengcheng,Li Zhenchun et al.3D first-arrival traveltime tomography with linearized eikonal and shaping regularization.OGP,2017,52(2):264-272.

[20] Hansen P C,O’Leary D P.The use of the L-curve in the regularization of discrete ill-posed problems.SIAM Journal on Scientific Computing,1993,14(6):1487-1503.