钢管混凝土核心柱节点有限元模拟
胡鹏飞 罗辉辉
(1.扬州大学建筑科学与工程学院,江苏 扬州 225127; 2.扬州大学广陵学院,江苏 扬州 225127)
0 引言
近年来,随着对既有房屋增层改造的兴起,不少学者[1-4]提出一系列新型框架结构,其中框架梁和框架柱多数采用型钢和钢筋混凝土材料的一种或两种结合制作而成,并取得一定研究成果[5,6]。但节点作为连接梁柱的关键部位,是结构安全工作的前提,目前仍未得到充分研究,尤其是钢管混凝土核心柱节点。
采取试验方法研究参数对钢管混凝土核心柱节点的影响,必然存在若研究参数多,对应的价格会提高问题,因此很多学者采用非线性软件作为另一种研究方法[7],本文在试验结果的基础上,建立钢管混凝土核心柱节点数值模型进行模拟分析,并与试验结果对比。
1 有限元模型的建立
1.1 材料本构
节点柱截面以混凝土受到约束作用的不同为根据分为保护层混凝土、钢管内混凝土和两者间混凝土;同样节点梁截面混凝土分为保护层混凝土和箍筋约束区混凝土,如图1所示。

节点梁内箍筋约束区混凝土、节点柱内钢管外部箍筋约束区混凝土及梁柱保护层混凝土的受压应力—应变关系采用Mander[8]模型;节点柱内钢管内混凝土的受压应力—应变关系采用韩林海[9]提出的适用于ABAQUS的本构模型;混凝土的受拉应力—应变关系采用过镇海[10]提出的双参数模型,工字钢、钢管、纵筋和箍筋均采用理想弹塑性本构模型[11-14]。
1.2 数值模型的建立
本文采用实体单元C3D8R来模拟混凝土;桁架单元T3D2模拟纵筋和箍筋;钢梁及钢管采用壳单元S4R来模拟。为了防止加载位置及约束位置产生应力集中,在各部位设置的垫板也采用壳单元S4R来模拟。
本文按照试验尺寸将数值模型分为混凝土节点、钢筋骨架和型钢骨架三部分,并且由于文献[15]指出建立数值模型可以不考虑钢管与混凝土之间的粘结滑移,所以通过嵌入技术将三部分形成整体分析。节点有限元模型划分如图2所示。
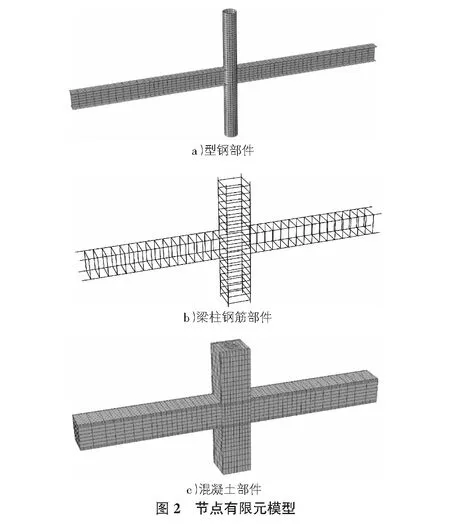
1.3 边界条件和荷载施加
根据试验设计,本文采用柱端加载的方法对试验试件进行模拟加载,约束柱底和梁端在平面内2个方向的平动。为了防止应力集中导致计算不收敛,将柱顶轴压力简化为面荷载施加在柱顶,同时在边界条件和荷载施加处设置刚度无限大垫板。通过位移控制的方法,在柱顶侧向垫块的中心施加相应的水平位移。最终模型的荷载、边界条件如图3所示。

2 结果分析
由于数值模型施加往复荷载不易收敛,且获得的滞回效果极不理想,所以本文仅对数值模型采取单调加载。
2.1 试验简介
试件按平面设计,不考虑平面外的影响,柱下端及梁端采用铰接连接,模拟柱身反弯点,钢管混凝土核心柱节点试件配筋图如图4所示。

实测钢管、工字钢、内环板屈服强度分别为255 MPa,288.1 MPa和291.2 MPa,实测钢筋直径8,12,25的屈服强度分别为388.4 MPa,402.3 MPa,445.3 MPa。实测混凝土立方体抗压强度为46.1 MPa。
2.2 结果对比
荷载—位移曲线与试验所得到的滞回曲线对比结果如图5所示,从图5中可以看出两者的初始刚度和最大承载力基本吻合,表明本文所建立的数值模型的正确性。

2.3 破坏形态对比

由于本文仅对数值模型进行单调加载模拟分析,所以该模型的破坏形态仅存在一个方向加载到最大水平位移时的破坏形态。图6给出了混凝土部件在极限荷载时沿水平方向(X方向)的应变E11分布,从图6中可以看出,在单调加载的情况下,梁端混凝土分别出现受拉和受压区,核心区混凝土沿对角线方向出现拉应变,其结果与试验最终的破坏形态如图6所示的梁端混凝土压碎剥落,核心区混凝土沿对角线发生剪切破坏的结果是一致的。
3 结语
本文通过对一个钢管混凝土核心柱节点试件建立数值模型研究分析,得到如下结论:
1)二次缩减实体单元能减少单元划分数,提高计算效率。
2)对梁柱截面混凝土划分不同区域并选用合理的本构关系,可以最大程度模拟试验条件,验证试验结果。
3)有限元模拟所得出的荷载位移曲线与试验滞回曲线对比发现两者的初始刚度和最大承载力基本吻合,验证了数值模型的合理性。
4)有限元模拟节点的破坏形态和试验结果基本一致,表明本文所建立的模型具有一定的可靠性。
参考文献:
[1] 薛伟辰,杨 枫,苏旭霖,等.预应力钢骨混凝土梁低周反复荷载试验研究[J].哈尔滨工业大学学报,2007,39(8):1187-1190.
[2] 傅传国,李玉莹,孙晓波,等.预应力及非预应力型钢混凝土框架受力及抗震性能试验研究[J].建筑结构学报,2010,31(8):15-21.
[3] 王 琨,袁沈峰,曹大富.配置核心钢管的钢筋混凝土柱—钢骨混凝土梁组合框架抗震性能试验研究[J].建筑结构学报,2013,34(6):103-112.
[4] 王 琨,袁沈峰,曹大富,等.型钢混凝土梁—角钢混凝土柱框架恢复力模型特性研究[J].北京理工大学学报,2014,34(10):1012-1017.
[5] 王文达,韩林海,陶 忠.钢管混凝土柱—钢梁平面框架抗震性能的试验研究[J].建筑结构学报,2006,27(3):48-58.
[6] 郑文忠,王 琨.型钢混凝土梁—角钢混凝土柱框架抗震性能试验研究[J].土木工程学报,2011,44(3):49-60.
[7] 王 琨,袁沈峰,智海祥,等.配置核心钢管的钢筋混凝土柱—钢骨混凝土梁组合框架力学性能非线性分析[J].工程力学,2016,33(10):197-207,217.
[8] J.B.Mander,M.J.N.Priestley,R.Park.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,ASCE,1988(114):1804-1826.
[9] 韩林海.钢管混凝土结构:理论与实践[M].北京:科学出版社,2007.
[10] GB 50010—2002,混凝土结构设计规范[S].
[11] J.Bauschinger.Variations in the Elastic Limit of Iron and Steel[J].Journal of Iron and Steel Inst,1887(1):442-444.
[12] W.Ramberg,W.R.Osgood.Description of Stress-strain Curves by Three Parameters.Technial note 902[J].National Advisory Committee on Aeronautics,Wahsington,D.C,1943(7):21-36.
[13] N.Abdel-Rahman,K.S.Sivakumaran.Material Properties Models for Analysis of Cold-formed Steel Members[J].Journal of Structural Engineering,ASCE,1997,123(9):1135-1143.
[14] K.W.Karren.Corner Properties of Cold-formed Steel Shapes [J].Journal of Structural Engineering,ASCE,1967,93(ST1):401-432.
[15] 廖飞宇,韩林海.方形钢管混凝土叠合柱的力学性能研究[J].工程力学,2010,27(4):153-162.

