半直驱风力发电机组联轴器胀紧套优化分析

赵春雨， 柳胜举

（明阳智慧能源集团股份公司，广东中山528437）

0 引言

风力发电是这一种新型、绿色无污染的能源实现方案，随着人们对环境、气候等因素的关注，风力发电等绿色能源逐步被人们接受，且呈现快速增长趋势[1-3]。在风电产业发展过程中，随着可利用风资源的急剧减少[4]，风机的生存环境越来越恶劣，许多的设计问题不断呈现出来，这些问题影响着机组的安全以及正常运行，因此对风机各部件的详细研究成为风机稳定运行的必要前提。

联轴器是连接齿轮箱与发电机的关键部件，它通过胀紧套与输入轴进行连接[5-6]。通过胀紧套安装螺栓的预紧，使外环相对胀紧套锥面进行移动，产生径向胀紧力，保证胀紧套与输入轴的紧密配合。在胀紧力作用下，需要保证连接轴、胀紧套以及外环有足够的强度，不会产生屈服破坏[7]。同时保证从输入轴通过胀紧套向输出轴的转矩传递，不会发生打滑现象。因此这就需要胀紧套外圈相对内圈的位移、胀紧套的锥面结构以及螺栓预紧力满足一定要求，来保证胀紧套的功能以及强度要求[8]。

1 理论分析

联轴器几何模型如图1所示，由胀紧套、外圈以及胀紧螺栓组成，对胀紧螺栓施加一定的预紧力，外圈与胀紧套产生相对位移，由于胀紧套外表面与外圈的结合面有一定的锥角，所以随着二者的相对移动，外圈对胀紧套产生挤压变形，导致胀紧套对连接轴产生压力。在该压力产生的摩擦力的作用下，实现输入轴的转矩向输出轴的传递。

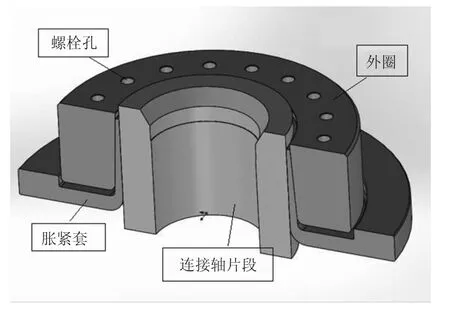
图1 几何模型

根据胀紧套受力特点，可以知道胀紧力的大小受到胀紧套外表面的锥角以及二者相对位移大小的影响，所以在初始设计时可以通过调整这2个参数以保证胀紧套对传动轴传递转矩的控制。胀紧力越大，可以传递的转矩越大，但各部分受到的应力也越大。因此在保证可以传递机组特定转矩的前提下，需要保证各部件的强度满足要求。

对于空心轴，在胀紧压力的作用下，各位置的应力计算公式如下[9]：

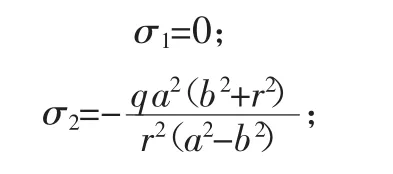
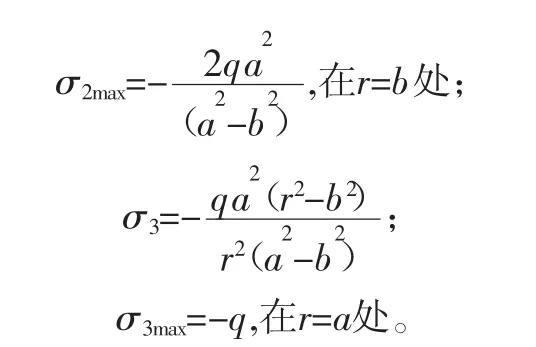
其中：σ1为纵向应力；σ2为周向应力；σ3为径向应力，拉为正、压为负；a为传动轴外径；b为传动轴内径；q为均布压力；r为传动轴径向某一处位置。

由以上公式可以看出，在胀紧力作用下，空心轴外部承受最大的径向应力，大小为胀紧压力，空心轴内部承受最大的周向应力。且从公式可以看出，内部周向应力永远大于外部径向应力，所以对胀紧套设计计算时，要充分考虑连接轴的内外径尺寸以保证轴的安全。对于外圈以及胀紧套，由于结构形状不规则，同时存在应力集中的特征，所以不适合采用理论公式进行分析。

随着计算机技术以及CAE仿真水平的高速发展，通过有限元方法可以很快得到各部件的应力结果、胀紧力的大小以及所需的螺栓预紧力[10-12]。

2 有限元分析

联轴器各部分材料：胀紧套材料为42CrMo4V：Rp0.2＞600 MPa；外圈材料为30CrNiMo8（EN 10083-3），Rp0.2＞800 MPa；空心轴材料为18CrNiMo7-6（EN10084），Rp0.2＞850 MPa。

图2 有限元模型

图3 边界条件

图4 空心轴应力云图

采用高阶六面体单元对联轴器以及螺栓进行网格划分[13]，共有节点861 829个，单元245 149个，有限元模型如图2所示。

足球运动已经在世界范围内产生了极大的影响，究其原因，就是因为该运动是在游戏的基础上发展而来的，极具趣味性与娱乐性，整个运动项目中都呈现出了生动性、竞争性、对抗性、丰富性等特点，所以一直以来被人们所喜爱。

按照初始设计要求，通过18颗螺栓预紧加载实现胀紧距离11.7 mm，由此确定初始计算模型的边界条件如图3所示。

经过有限元求解，空心轴的最大应力为491.3 MPa，满足要求；胀紧套圆角位置最大应力800 MPa，不满足要求，如图4、图5所示。由此可见按照施加预紧方式，原始设计不能满足强度要求。

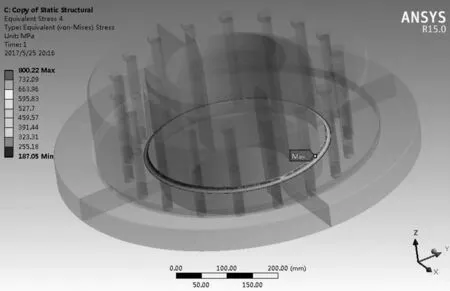
图5 胀紧套圆角应力云图

图6 胀紧套变形图

2.1 强度校核及优化

上述不满足强度要求的部位，主要发生在圆角位置，基于结构特点和优化思想，可以通过增大圆角来减小圆角处应力集中，或增厚胀紧套厚度来降低应力，但这种方法都需要重新设计模型，造成时间和成本的浪费。

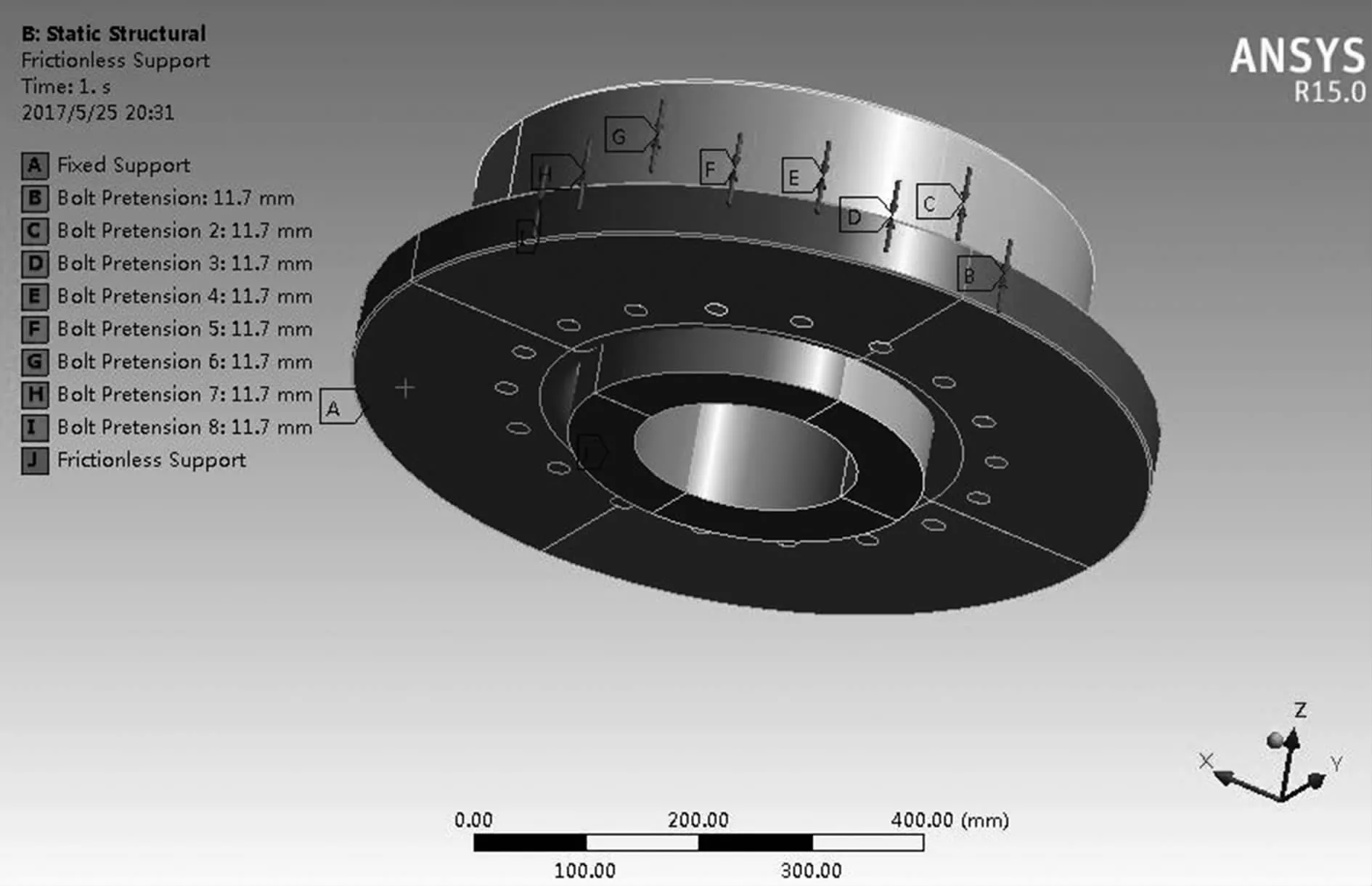
图7 优化后的边界条件

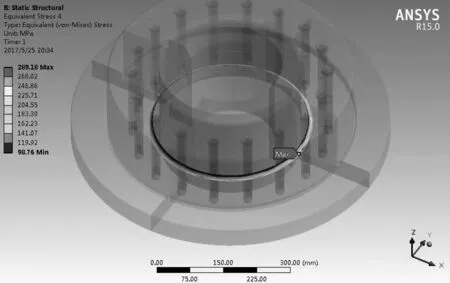
图8 优化后的胀紧套圆角应力图

经过对有限元分析变形结果进行研究不难发现，圆角处的过大应力是因为胀紧时空心轴处于自由状态，导致胀紧过程中没有外界约束限制胀紧套变形，如图6所示。因此，通过优化边界条件设置，除了约束胀紧套外缘全部自由度外，同时约束空心轴下端面的轴向自由度，如图7所示。

对优化边界后的模型进行分析，结果如图8所示，胀紧套圆角处应力仅有289 MPa，满足要求。

这说明在进行胀紧套安装预紧时，安装工艺要保证传动轴的轴向不会发生窜动，从而保证胀紧套在安装过程中的安全性。这种优化方法，仅需变更安装工艺，无需对结构进行修改，节省了设计周期和成本。

2.2 螺栓规格选型

由胀紧套的工作原理可知，胀紧距离的实现是通过对18颗螺栓施加预紧力，从而带动外圈与胀紧套内圈之间发生相对移动来实现，如果螺栓规格选择太小，则外圈相对胀紧套不能安装到位，也不能达到所需的胀紧力；如果螺栓规格选择过大，则结构的尺寸就会增大，螺栓成本也会增加，所以确定合理的螺栓规格非常重要[14-15]。

其中：FMzul为螺栓预紧力；A0为螺栓应力圆面积；v为螺栓预紧时屈服应力利用系数；Rp0.2min为螺栓屈服应力；d0为应力圆直径；d2为螺栓节圆直径；P为螺栓节距；μGmin为螺纹摩擦因数。

根据螺栓拉伸力公式以及有限元结果中提取的最大螺栓支反力，同时屈服应力利用系数v小于1的情况下，计算得到螺栓应力面积，并依此确定螺栓规格。经计算，为满足胀紧安装工艺的要求，应选取不小于M20规格的螺栓。

2.3 极限转矩计算

从前面分析可知胀紧安装距离以及胀紧套锥角影响胀紧力的大小，而胀紧套对空心轴的压力产生的摩擦力决定了联轴器传递的最大转矩。

通过对胀紧套与空心轴接触面上的压力进行积分，得到接触面上压力和。也可以通过提取有限元模型中接触面上的径向支反力得到总的胀紧压力。

从胀紧套有限元模型分析中，可以得到接触面上径向支反力为2.2×107N，假设胀紧套与传动轴之间的摩擦因数为0.15，空心轴外径为0.32 m，则可以传递转矩为T=P·μ·R=527 kN·m。

由此可以发现，影响传递转矩的大小的因素为胀紧套与传动轴之间摩擦因数、传动轴外径、胀紧安装距离、胀紧套锥角。当打滑力矩不能满足要求时，可以通过修改以上几个参数进行优化调整。

3 结论

经过以上分析可以看出：1）在胀紧力一定的前提下，传动轴的安全性与轴径有关，内外径比例越大，安全性越高；2）胀紧套的优化，除了可以通过调整胀紧套结构外，还可以通过优化安装工艺来实现。保证在安装过程中传动轴的轴向固定，可以降低胀紧套的受力；3）螺栓规格的选取，不仅要满足胀紧力的要求，还要保证螺栓本身的安全性；4）胀紧套可以传递的转矩与表面摩擦因数、传动轴外径、胀紧安装距离、胀紧套锥角有关。通过对胀紧套本身强度、连接轴强度、装配工艺、装配螺栓选型、打滑力矩等方面的研究，为联轴器胀紧套的最优化设计提供了依据。

[参 考 文 献]

[1] 侯侠,王静.21世纪的绿色能源[J].内蒙古石油化工,2006(12)：52-54.

[2] 程启明,程尹曼,王映斐,等.风力发电系统技术的发展综述[J].自动化仪表,2012,33(1)：1-8.

[3] 李军军,吴政球,谭勋琼,等.风力发电及其技术发展综述[J].电力建设,2011,32(8)：64-72.

[4] 李斌,张宇时.低风速风电场资源开发的探讨及应用[J].分布式能源,2017,2(2)：44-50.

[5] 刘辉,项昌乐.弹性联轴器对动力传动系统扭振特性影响研究[J].机械强度,2009,31(3)：349-354.

[6] 彭浩坤,贾军朋,秦中正,等.风电联轴器传动轴同轴度误差影响动平衡的计算[J].机械研究与应用,2016(6)：90-96.

[7] 王颜辉,郭强.风电胀紧套的力学行为分析[J].山西煤炭管理干部学院学报,2015,28(1)：88-90.

[8] 赵涛.风力发电机组胀紧套联接的应用与设计计算[C]//2014年第四届全国地方机械工程学会学术年会暨新能源装备制造发展论坛论文集.2014：286-288.

[9] YOUNG W C,BUDYNAS R G.Roark’s Formulas for Stress and Strain[M].McGraw Hill,2002.

[10] 叶又,彭颖红,阮雪榆.计算机仿真技术在制造业中的应用[J].机械工程师,1996(6)：49-50.

[11]朱金光,冷峻,刘安宁,等.CAE分析在企业技术创新中的初步探索与实践[J].农业装备与车辆工程,2008(10)：35-37.

[12]张树桐.浅谈计算机辅助工程(CAE)的发展及应用[J].信息科技,2010(8)：232-233.

[13]吕建国,康士廷.ANSYS Workbench14有限元分析自学手册[M].北京：人民邮电出版社,2013：99-130.

[14] 濮良贵,纪名刚.机械设计[M].8版.北京：高等教育出版社,2007：62-101.

[15] 成大先.机械设计手册[M].6版.北京：化学工业出版社,2017：14-25.

[16]VDI 2230 Part 1,Systematic calculation of High Duty Bolted Joints,Joints with One Cylindrical Bolt [Z].Düsseldorf,Germany：Vere in DeutscherIngenieure,2015.