基于模型预测控制的电动轮车辆横摆控制

严运兵，叶 刚，许小伟，张振宇

(武汉科技大学汽车与交通工程学院，湖北 武汉，430065)

为了提高汽车的操作稳定性，车辆稳定控制(Vehicle Stability Control, VSC)及电子稳定程序(Electronic Stability Program, ESP)等主动安全控制系统得到广泛运用。ESP与VSC将车辆的横摆角速度作为稳定性控制变量，通过电子控制单元控制前后、左右车轮的制动力，产生附加横摆力矩，确保车辆行驶的横摆及侧向稳定性。单纯控制横摆角速度在附着良好的路面条件下能够取得较好的控制效果，但在附着系数较低的路面上无法保证操作稳定性[1]。质心侧偏角作为车辆稳定性控制中的另一个控制变量，反映了车辆偏离期望轨迹的程度。在附着系数较低的路面上，车轮可利用的侧向力很小，车身整体沿侧向滑动的趋势要强于横摆运动[2]，所以在车辆稳定性控制中，对质心侧偏角进行控制能够避免车辆失去侧向力而偏出期望轨迹。根据轮胎的附着特性，不同路面的侧向力饱和值相差很大，故质心侧偏角安全边界值也有所差异[3]。利用横摆角速度和质心侧偏角之间的耦合关系设计控制器，在附着性不同的路面上既能使横摆角速度跟踪驾驶员的期望，实现顺利转向，又能将质心侧偏角限定在安全范围内，提高主动安全控制系统的工作性能。

本文针对四驱电动轮汽车，结合其四轮独立驱动/制动的特点，建立了8自由度整车模型，基于鲁棒性强、在线实时性好的模型预测控制(Model Predictive Control，MPC)方法[4]设计控制方案，以根据路面附着系数不同而变化的质心侧偏角动态稳定边界作为输出约束、以电机饱和输出力矩作为控制输入约束，在保证质心侧偏角稳定的前提下，使实际横摆角速度较好地跟踪其理想值，以期车辆在附着性不同的路面上均能实现比较理想的控制效果。

1 整车及轮胎模型

1.1 8自由度整车模型

针对电动轮车辆各驱动力可单独控制的特点，并结合载荷转移引起的轮胎力变化对车辆操纵性及稳定性的影响，建立一个包括纵向、侧向、横摆、侧倾及4个车轮转动的车辆模型，为控制策略的制定提供依据。控制对象的8自由度模型如图1所示，图中，Fsi、Fti(i=1,2,3,4)为轮胎侧向力和纵向力，β为质心侧偏角，γ为横摆角速度，δ为汽车前轮转角，vx、vy为车辆行驶速度。车辆及轮毂电机参数值如表1所示。

整车纵向、横摆、侧向、侧倾以及车轮转动的运动方程为：

(1)

(2)

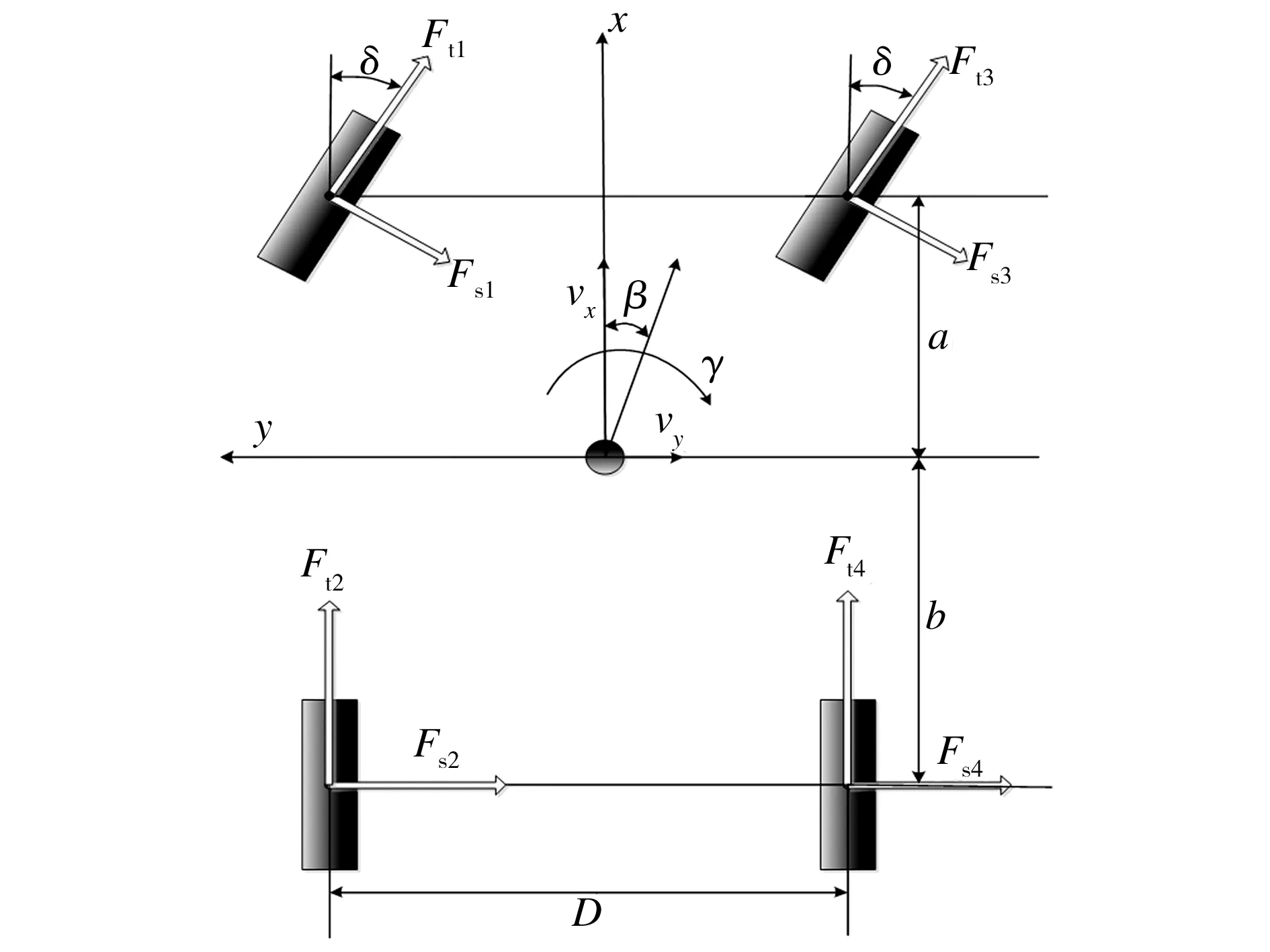
图1 8自由度车辆模型

参数数值整车质量m/kg1240质心到前后轴的距离(a,b)/m1.157,1.453整车绕z轴的转动惯量Iz/kg·m21622悬挂质量ms/kg970整车绕侧倾轴线转动惯量Ix/kg·m2302车身侧倾阻尼系数Cq/N·m·rad-12600前后轴距l/m2.61悬挂质量质心到侧倾轴线的距离hs/m0.485前、后轮纵向刚度Ks/N·rad-153081,54526前、后轮侧向刚度Kα/N·rad-141710,26681电动轮转动惯量J/kg·m22.5车轮半径R/m0.3075汽车轮距D/m1.463轮毂电机类型永磁直流无刷额定功率P/kW3.0最大输出功率Pmax/kW7.2额定转速n/r·min-1750额定电压U/V72额定电流I/A95

(3)

(4)

(5)

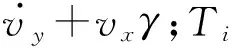
1.2 Dugoff轮胎模型

仿真中采用 Dugoff 非线性轮胎模型，该模型考虑了载荷、滑移率、侧偏角和路面附着系数对轮胎力的影响，能较好地描述轮胎的非线性特性，其表达式如下：

(6)

2 模型预测控制

2.1 模型预测控制基本原理

本文基于MPC设计采用直接横摆力矩控制的上层运动跟踪控制器，在满足跟随车辆理想响应及质心侧偏角安全约束的条件下，确定下层控制器的控制输入，即附加横摆力矩。

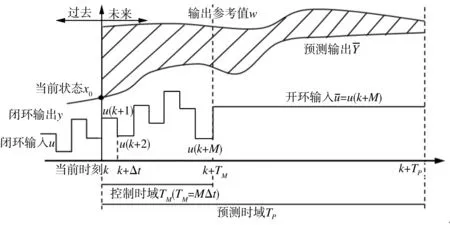
图2 模型预测控制原理示意图

2.2 预测模型

预测控制是一种基于模型的控制算法，其预测模型具有展示系统未来动态行为的功能，可以根据历史信息和假设的未来输入预测出车辆的未来状态或输出，传递函数、状态方程都可以作为预测模型[5-6]。本文在设计预测模型时，车辆被简化成以状态空间形式表述的2自由度模型，该模型能够预测出有附加横摆力矩输入时车辆的未来运动状态。鉴于质心侧偏角β和横摆角速度γ与车辆稳定性的关系最为密切，如果把β和γ作为状态变量、汽车的前轮转角δ作为输入，则暂不考虑附加横摆力矩输入的汽车线性2自由度操纵模型可以用下列状态方程描述：

(7)

在预测算法中，产生的附加横摆力矩记为Ma，并将其作为控制输入，则式(7)可改写成

(8)

(9)

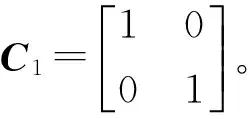
3 模型预测控制器设计

3.1 控制输入和输出约束

在车辆转向过程中，当路面附着系数较低或纵向力需求较大时，轮胎的侧向力趋于饱和，提供的反力无法克服车辆在转向过程中的离心力，车辆可能前轴侧滑，偏离期望轨迹，或是后轴侧滑急转甩尾，甚至还会导致侧翻等不可控的局面。本文采用质心侧偏角控制策略，通过限制质心侧偏角的大小，使轮胎侧向力不超过饱和边界范围，避免失稳状态发生[7]。

由于不同的路面上车轮的侧向力饱和值以及质心侧偏角的安全区间相差很大,因此本文采用动态质心控制准则设计模型预测控制器，在满足|β|≤arctan(0.02μg)[1]的控制输出约束的同时，使车辆的横摆角速度跟踪理想值，增强控制器对不同路面的适应能力。

2自由度汽车动力学模型能很好地反映汽车的运动状态，常以稳态下前轮转向车辆的横摆角速度作为理想值，其计算公式为[8]：

(10)

电机最大输出力矩不是定值，取决于电机的供电电压及转速，由于控制器作用时间内电压的变化很小，可认为电机的最大输出力矩只与转速相关。通过查询电机的外特性曲线图，可知当前时刻驱动电机的最大输出力矩[9]，记为Tmax。结合车辆相关参数及一定的力矩分配方法，可得出当前时刻驱动系统能提供的最大附加横摆力矩：

(11)

式中：f为车辆行驶中的各类阻力之和。因此系统的控制输入约束为：

u(k+i)≤umax(k+i)=Ma,max(k+i),

i=1,…,M

(12)

3.2 控制流程

在车辆行驶过程中，由于路面因素或车辆自身原因导致其运动状态与期望状态有所差别时，通过控制驱动电机的输出力矩来获得相应的横摆力矩进而调整汽车的运行状态，使车辆按照期望的轨迹行驶，其控制流程如图3所示。2自由度模型通过采集前轮转角、车速等信息，计算出理想横摆角速度γd作为控制器的参考输入，将安全的质心侧偏角作为输出约束，结合电机模型实时计算出理想的附加横摆力矩，横摆力矩分配模块计算出每个车轮需要施加的驱动力或制动力。

将式(9)以采样周期Δt为步长进行离散化：

图3 控制流程

x(k+1)=Ax(k)+Bu(k)

y(k)=Cx(k)

(13)

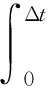
由模型预测控制理论可知，假设从k时刻起，附加的横摆力矩Ma发生M步变化，然后保持不变，根据式(13)可以预测出，在Ma(k+1)、Ma(k+2)、…、Ma(k+M)作用下，P(P≥M)个时刻的系统输出为

y(k)=Fyx(k)+Gyu(k)

(14)

3.3 滚动优化

因为车辆直接横摆力矩的作用是使实际横摆力矩在未来P个时刻的预测值y(k+i)尽可能地接近给定的期望值w(k+i)，i=1,…,P，同时使控制输入尽可能小，因此可以用二次型写出性能指标的向量形式：

(15)

式中：w(k)=[w(k+1),…,w(k+P)]T是期望的横摆角速度输出值的向量表达形式；Qy、Ry是适当维数的输出加权矩阵和控制加权矩阵，其中，Qy=diag(q1,q2,…,qP)，Ry=diag(r1,r2,…,rM)，q和r均为正数。

输出加权矩阵越大，系统的输出即理想横摆角速度和实际横摆角速度的偏差越接近0；控制加权矩阵越大，对控制输入的抑制作用越明显。

通过MATLAB MPC工具箱调整输出加权矩阵控制质心侧偏角在安全范围内，使横摆角速度能较快地跟踪理想值。由上述分析并结合式(12)和式(13)，直接横摆力矩控制问题可表述为：

(16)

式中：e=[1,0]；d=arctan(0.02μg)。

在有约束的情况下，预测控制需要在控制时域的每一个时刻求解形如式(16)的具有二次型性能指标且带不等式约束的优化问题，这是一个二次规划问题。对于这样一个在线优化问题，将优化指标中的y(k)用预测模型代入，则J(k)可改写成：

J(k)=[w(k)-Fyx0(k)]TQy[w(k)Fyx0(k)]-

2[w(k)-Fyx0(k)]TQyGyu(k)+

(17)

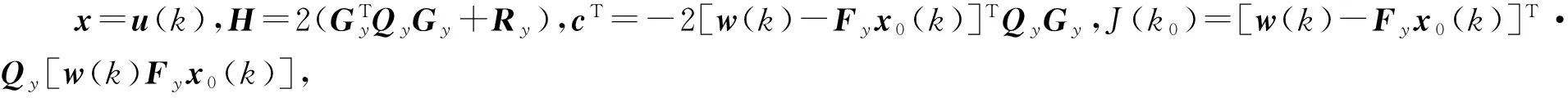
(18)

由于式(18)中J(k0)为k时刻的已知项，与优化无关，可从性能指标中除去，则上式可以化成标准二次规划问题：

(19)

根据其定义可知矩阵H≥0。如果H是半正定的，则该问题是一个凸二次规划问题，有一个全局最小值；如果H是正定的，则其为严格的凸二次规划问题，全局最小值就是唯一的。

对如式(16)所示的不等式约束二次规划，常采用有效集(Active Set)方法求解[10]。此时的解记U(k)=x=[u(k+1),u(k+2),…,u(k+M)]，根据模型预测控制的基本原理，将这一系列解的第一个元素u(k+1)应用到车辆控制中。

3.4 直接横摆力矩的实现方法

为了以较小的驱动力矩变化来获得较理想的直接横摆力矩，同时保证总的纵向驱动力恒定，本文采取的控制方法是：将一侧前后车轮的驱动力减小一定值，另一侧的前后轮则增加相同大小的驱动力。当纵向驱动力没有较大变化时，可以认为在预测时域内纵向车速是恒定不变的。每个驱动轮增加或减小的驱动力矩计算公式为：

(20)

4 仿真与结果分析

为验证本文所提方法的控制效果，设置两种仿真工况：①良好路面(附着系数为0.85)，车辆高速(110 km/h)行驶；②湿滑路面(附着系数为0.3)，车辆中低速(40 km/h)行驶。采用Simulink搭建8-DOF汽车模型，对前轮分别施加阶跃输入和正弦输入，仿真得出车辆质心侧偏角、横摆角速度的时间响应曲线以及车辆的行驶轨迹图。

4.1 良好路面仿真分析

汽车在良好路面上以110 km/h的速度匀速行驶，在第10 s时分别对前轮施加5.73°阶跃输入和幅值为10°、周期为4 s的正弦输入，仿真结果见图4。可以看出，在良好路面上高速行驶并且进行紧急大转角避让障碍物或是紧急换道操作时，无论是否对横摆力矩进行控制，车辆都能够完成相应的操作。对前轮施加阶跃输入时，两种车辆的横摆角速度的超调量均较大，但有MPC控制车辆的横摆角速度很快趋于稳定，稳态偏差较小，且质心侧偏角得到了很好的抑制，没有超出安全范围，从车辆行驶轨迹中可知此时其转弯半径有所增大；对前轮施加正弦输入时，有MPC控制车辆的横摆角速度能较好地跟踪理想值，质心侧偏角波动较小，没有超出安全范围，能够按照期望的路径完成变道操作，转向更为稳定、迅速，车体侧向摆动及侧向偏移量小，而未控制车辆的质心侧偏角明显超过安全阈值。

(a)阶跃输入

(b)正弦输入

图4良好路面上的仿真结果

Fig.4Simulationresultsontheroadwithhighadhesioncoefficient

4.2 湿滑路面仿真分析

汽车在湿滑路面(附着系数为0.3)上以40 km/h匀速行驶，在第10 s时分别对前轮施加11.4°阶跃输入和幅值为10°、周期为4 s的正弦输入，仿真结果见图5。可以看出，在湿滑路面上，由于路面附着系数较小，轮胎侧向力已趋于饱和，在两种输入情况下，未控制车辆的质心侧偏角都出现了较大波动并超过其安全阈值，表现为车辆的侧向不可控位移急剧增大，车辆的横摆角速度剧烈波动，无法跟踪理想值，车辆可操纵性很差。而MPC控制器能够减小车辆质心侧偏角，使其较快趋于稳定，基本处于安全范围内，而且车辆横摆角速度也能很好地跟踪理想值。从车辆行驶轨迹来看，有MPC控制的车辆在前轮阶跃输入时能够减小车辆的转弯半径，在前轮正弦输入时能够减小侧向滑移，保证车辆行驶轨迹基本符合预期。

(a)阶跃输入

(b)正弦输入

图5湿滑路面上的仿真结果

Fig.5Simulationresultsontheroadwithlowadhesioncoefficient

5 结语

四轮毂独立驱动车辆为直接横摆力矩控制的实现提供了比集中式驱动更加多样而直接的控制方式。本文采用模型预测控制算法，以根据轮毂电机的最大输出力矩计算得到的附加横摆力矩作为控制输入约束，以根据不同路面性质得到的质心侧偏角安全阈值作为输出约束，在此前提下保证车辆的横摆角速度跟踪理想值，然后将在线计算得到的附加横摆力矩通过特定方式分配给驱动电机。这种控制策略能够兼顾多种工况下车辆的稳定性和可操纵性，使其转向平稳、迅速，车辆循迹能力得到提高。

由于本文主要研究电动轮车辆在转向工况下的横摆稳定性，并不涉及舒适性和车辆紧急制动、加速的情况，因此没有考虑车辆悬架的垂直方向动态特性，并忽略了车身的俯仰运动。所采用的Dugoff轮胎模型及8自由度整车模型反映了横摆稳定性控制中轮胎及车身的主要动力学和运动学特征，将其作为控制对象，在保证仿真精度的同时，能够提高运算速度。

鉴于本文控制算法涉及大量的矩阵运算，计算量较大在一定程度上会影响控制系统的实时性，而且附加横摆力矩采用的是两侧力矩大小相同、方向相反的原则进行分配的，该方法比较直接，计算方便，但不足之处是没有考虑不同车轮之

间的差异性，没有得到附加横摆力矩的最佳分配方案。对有约束的MPC控制算法以及横摆力矩的分配方式进行优化，这有待于后续研究中解决。

参考文献

[1] 陈无畏,刘翔宇,黄鹤,等.考虑路面影响的车辆稳定性控制质心侧偏角动态边界控制[J].机械工程学报,2012,48(14):112-118.

[2] 张晨晨,夏群生,何乐.质心侧偏角对车辆稳定性影响的研究[J].汽车工程,2011,33(4):277-282.

[3] 陈无畏,王其东,肖寒松,等.汽车系统动力学与集成控制[M].北京:科学出版社,2014.

[4] Falcone P, Tseng H E, Borrelli F, et al. MPC-based yaw and lateral stabilisation via active front steering and braking[J]. Vehicle System Dynamics, 2008, 46(S1): 611-628.

[5] 席裕庚,李德伟,林姝.模型预测控制——现状与挑战[J]. 自动化学报,2013,39(3):222-236.

[6] Huang X Y, Wang J M. Model predictive regenerative braking control for lightweight electric vehicles with in-wheel motors[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2012,226(9):1220-1232.

[7] Chung T, Yi K. Design and evaluation of side slip angle-based vehicle stability control scheme on a virtual test track[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 224-234.

[8] 夏存良.基于纵向力分配及主动转向的底盘动力学控制方法研究[D].上海：同济大学,2007.

[9] 袁磊.四轮轮毂驱动电动汽车滑移率控制系统研究[D].长春:吉林大学,2016.

[10] 席裕庚.预测控制[M].北京:国防工业出版社,2013.