基于滑移/非滑移异质界面的动压润滑性能优化
吴振鹏,曾良才,林 广,湛从昌,陈新元
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.油威力液压科技股份有限公司,江苏 海门,226100)
采用织构化表面来改善流体动压润滑性能的方法已被广泛地研究与应用,而一种使用滑移/非滑移异质界面来影响流体动压的方法也得到越来越多的关注[1-2]。考虑到边界滑移条件,对于滑移/非滑移异质界面,经典雷诺方程不再适用,为此Spikes[3]建立了扩展形式的雷诺方程,并证明“半润湿性”轴承同时具有低摩擦、高承载能力的优越性能。Aurelian等[4]指出,布置合适的滑移/非滑移异质表面在提高轴承承载能力方面具有与织构相似的效果。Zhang等[5]对具有边界滑移区域的高速水润滑轴颈轴承进行数值计算,结果表明在轴颈轴承的套筒上布置合适的滑移/非滑移表面可以有效改善润滑性能,抑制空化现象的发生,减少壁面摩擦阻力,提高轴承承载能力。
然而,现有的异质界面滑移区和非滑移区的组合方式仍是单一的直线拼接式,并没有针对各类流体润滑摩擦副工况设计出相应的拼接方案。因此,如何在有限的区域内通过优化滑移区和非滑移区的拼接轨迹来改善流体动压润滑性能还有待于进一步研究,而目前采用的方法通常是分组设计样本并建模,然后分别对比研究其润滑性能,这样不仅样本数量有限而且模型建立过程繁琐,也难以得出规律性结论。
本文建立一组离散式二次方程描述滑移区和非滑移区的拼接轨迹,采用MATLAB软件进行仿真计算,并引入计算域单元宽长比作为仿真优化变量,分别以液膜刚度和摩擦因数作为优化目标,求解得出不同宽长比条件下滑移区和非滑移区的最优拼接轨迹。
1 模型的建立和求解
1.1 计算域
图1所示为基于直线拼接方式的异质界面动压润滑模型计算域。取一对相互平行的板作为研究对象,其中:下板为固定板,其表面的左侧一半设为滑移区;上板为运动板,以速度U沿x轴方向
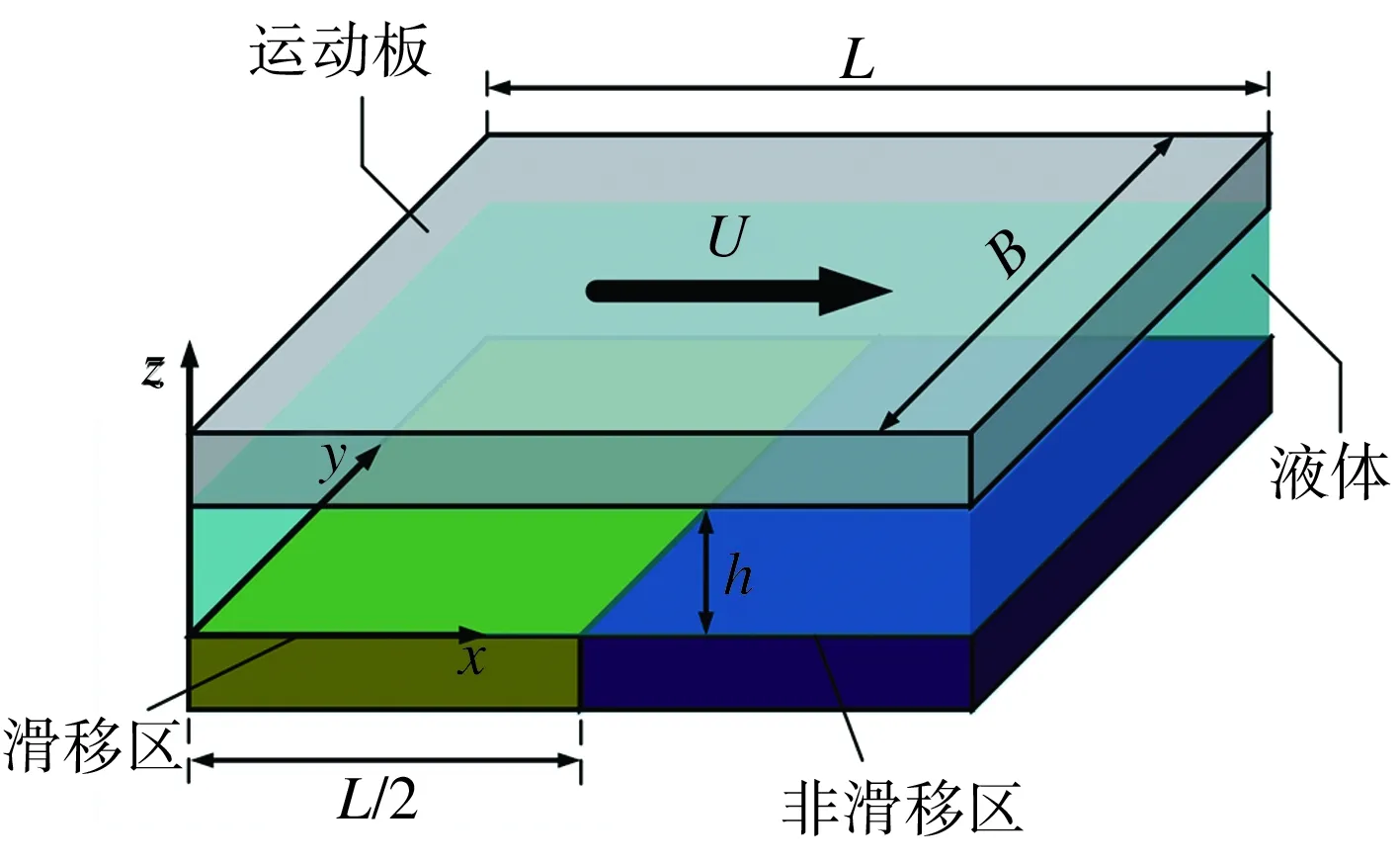
图1 计算域
运动。两板之间的间隙为h,并充满黏度为η的液体,因此h也是液膜厚度。两板的长度均为L,宽度均为B。
1.2 雷诺方程的扩展
假设滑移区近壁面上的液体流速不一定等于壁面运动速度,其余条件与文献[6]中经典雷诺方程推导的假设前提条件相同。按图1所示坐标轴创建笛卡尔坐标系,液膜中任意点的流速为[6]:
(1)
(2)
式中:u、v分别为流体沿x、y方向的流速;p为液膜压力;us、vs分别为处于下表面近壁层流体沿x、y方向的流速。
将式(1)和式(2)沿膜厚方向积分,可分别求得流体沿x、y方向的体积流量qx、qy,其表达式如下:
(3)
(4)
根据流体连续性条件[6],有:
(5)
将式(3)~式(5)联立,得到无量纲形式的扩展雷诺方程如下:
(6)
其中:
(7)
式中:p0为标准大气压。
根据Navier边界滑移条件,处于下表面近壁层的流体沿x、y方向的流速可由式(8)和式(9)表示[7]:
(8)
(9)
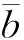
联立式(1)和式(8)、式(2)和式(9),可得:
(10)
(11)
根据图1所示滑移区的分布范围,可以给出下列边界条件:
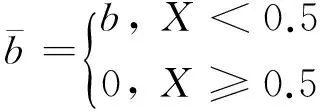
(12)
式中:b为滑移区内滑移长度。
假设计算域的入口、出口处的压力恒定并等于零,其描述如下:
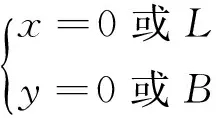
(13)
1.3 仿真计算
求解方法参照文献[8]采用松弛迭代法,根据流体动压润滑典型润滑膜厚的范围[6]、46号抗磨液压油的黏度以及文献[9]所总结的通过诸多试验测出的边界滑移长度范围选取仿真参数(见表1),得到液膜压力分布如图2所示。观察图2可知,越靠近滑移区和非滑移区的拼接线附近,液膜压力越大。因此,通过调控该拼接线的轨迹可以有效地改变液膜的压力等参数。
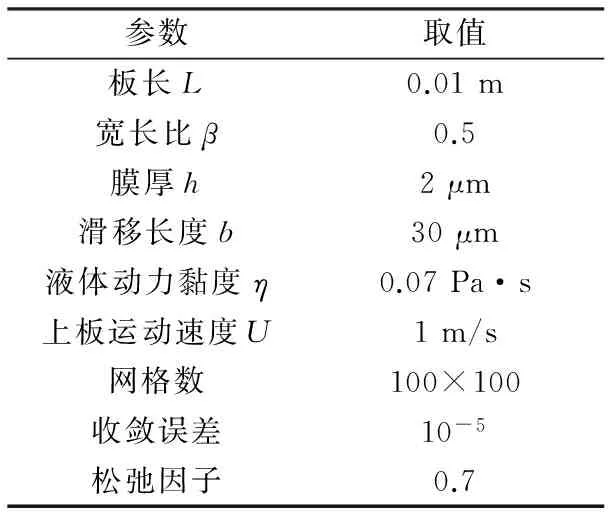
表1 仿真参数
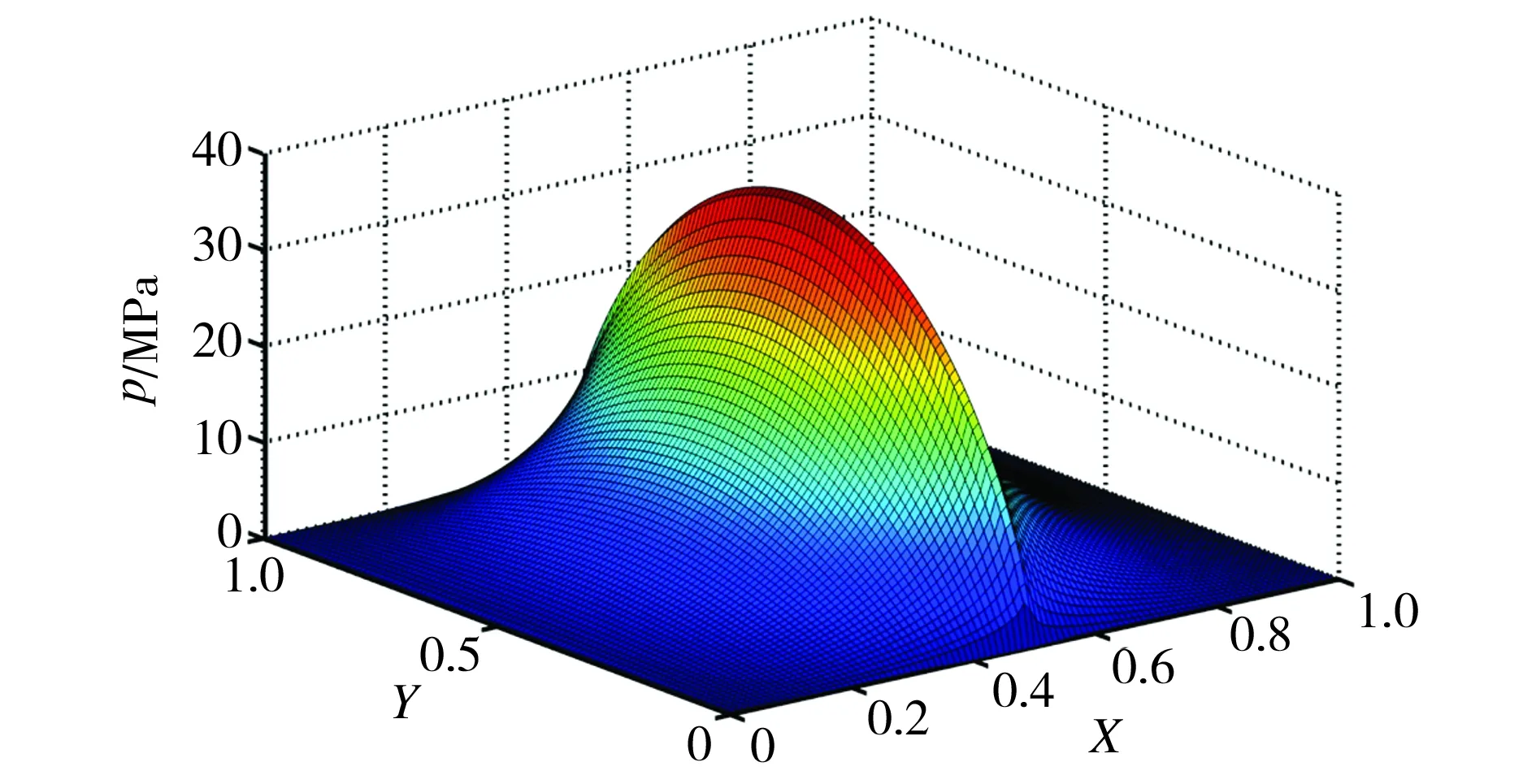
图2 液膜压力分布
2 动压润滑性能的优化
2.1 优化目标的确定
处于不同工况条件下的流体润滑摩擦副对液膜工作参数的要求是不同的。例如,对于能够长期达到流体润滑状态且负载波动不大的高速液体动压轴承,主要考虑液膜阻力造成的内摩擦功耗,而且因内摩擦功导致的温升会给油液带来诸多不利影响,因此,这种情况下有必要将决定液膜阻力作用程度的重要参数——摩擦因数作为动压润滑性能优化目标之一。另外,流体润滑摩擦副在工作状况下,由于机械自身的振动、活塞或轴的偏载等因素,使负载产生较大的波动,因此,如何提高液膜刚度,以最小的液膜厚度变化来应对负载的波动并达到持久的流体润滑状态就显得十分重要,因此本文将液膜刚度作为另一个优化目标。
2.2 拼接轨迹的建立
构建一组离散式二次方程来取代式(12)给出的边界条件:
(14)
式中:a∈ [-0.5,0.5];n=±1.08m,其中m=1,2,…,50。
该离散式方程所描述的拼接轨迹如图3所示。该方法仅采用一组二次方程、引入一个变量n就构造出了图3中分布较为连续的50组拼接轨迹样本,可以方便地带入迭代程序中进行优化求解。
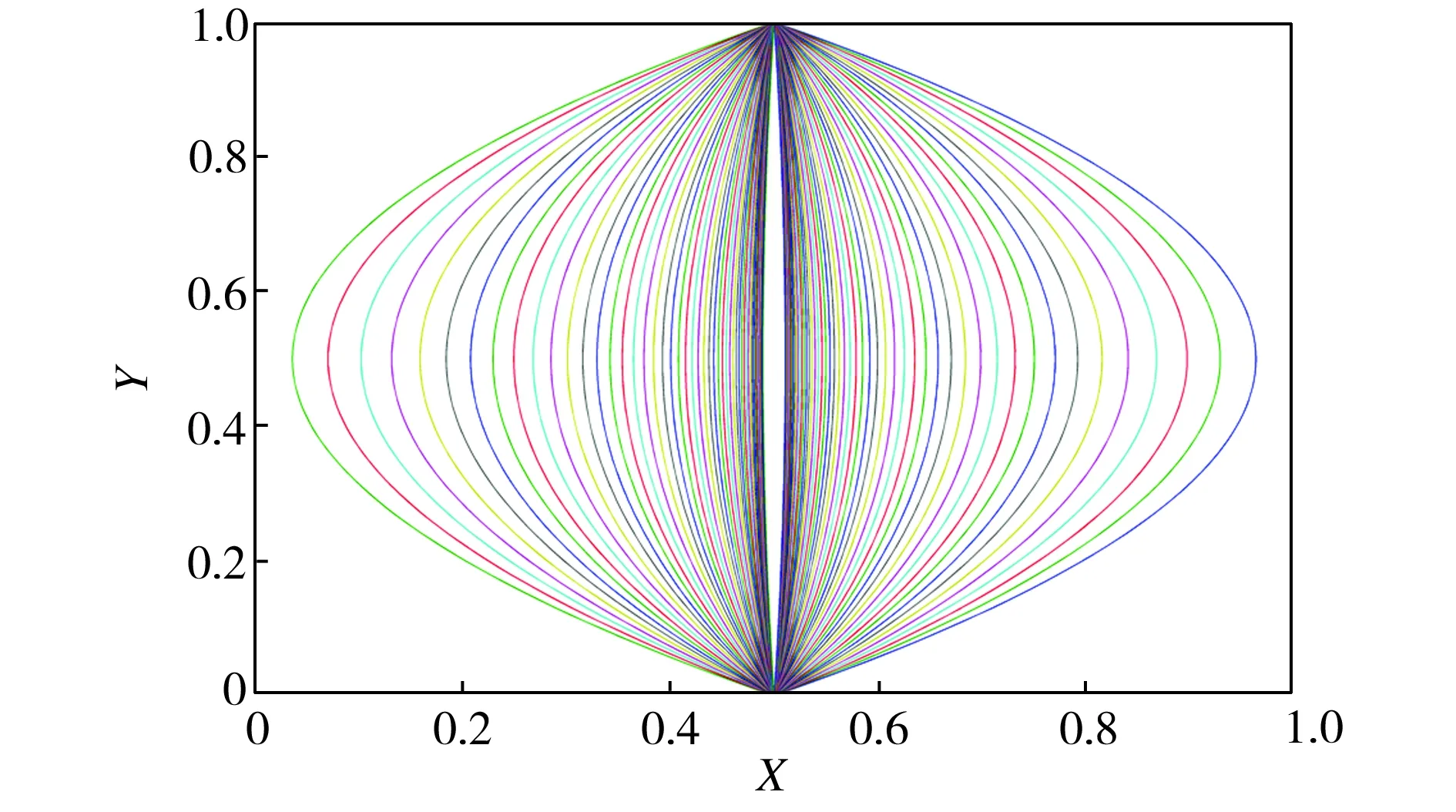
图3 拼接轨迹样本
2.3 摩擦因数的求解
根据牛顿黏性定律,液膜沿x方向作用在上板的剪切应力τx可表示为[6]:
(15)
将剪切应力沿整个液膜范围内积分,可以求得上板所受液膜的摩擦力Fx:
Fx=∬τxdxdy
(16)
将仿真得到的压力在整个液膜范围内积分,可求得液膜的承载力W:
W=∬pdxdy
(17)
进而可以确定摩擦因数:
(18)
2.4 液膜刚度的求解
考虑到计算域宽长比β及二次方程变量n等因素,采用差分方程来近似求解液膜刚度K[10]:
(19)
2.5 优化结果与分析
仿真优化计算仍采用松弛迭代法,优化变量β的取值范围为0.1~5,膜厚步长Δh=0.01 μm,其余参数同表1所示。
通过MATLAB计算得到摩擦因数μ与计算域宽长比β和二次方程变量n之间的关系如图4所示,可以发现,随着宽长比的增大,摩擦因数μ显著减小,而当β一定、变量n的取值趋近于0时,摩擦因数明显增大。
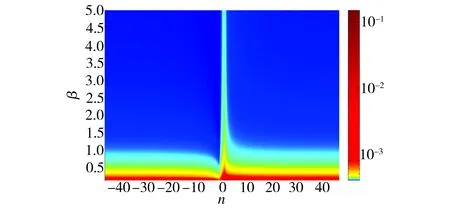
图4 摩擦因数μ随变量n和宽长比β的变化
Fig.4Variationoffrictioncoefficientμwithvariablenandaspectratioβ
液膜刚度K与计算域宽长比β和变量n之间的关系如图5所示。由图5可见,随着宽长比的增大,液膜刚度明显增大,同时,变量n对液膜刚度K的影响也极为明显。
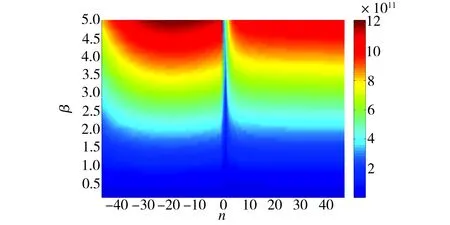
图5 液膜刚度K随变量n和宽长比β的变化
Fig.5VariationoffilmstiffnessKwithvariablenandaspectratioβ
综上所述,针对具有不同宽长比β的计算域,都可以找到一个最优的变量n来优化摩擦因数μ或液膜刚度K。将优化后的摩擦因数和液膜刚度与采用式(12)中的边界条件(即直线拼接方法)所求得的结果进行对比,如图6~图7所示。由图可知,与采用直线拼接方法相比,选取二次方程所描述的抛物线作为滑移区和非滑移区拼接轨迹的方法在摩擦因数和液膜刚度这两个优化目标上都能有所改善。
针对任意一个宽长比β取值,可以确定与最优参数所对应的n值。图8所示为β取值不同时摩擦因数和n之间的关系。以β=0.5为例,摩擦因数最小时所对应的n=-1.26,因此,将该值带入原二次方程,即可绘制出与之对应的最优拼接方案,如图9所示。结合图6中β=0.5时的数据可知,在同一区域内,由于采用了图9中的拼接方式,摩擦因数由优化前的0.0027减至0.0013。

图6 优化前后摩擦因数μ与宽长比β之间的关系
Fig.6Relationshipbetweenfrictioncoefficientμandaspectratioβbeforeandafteroptimization
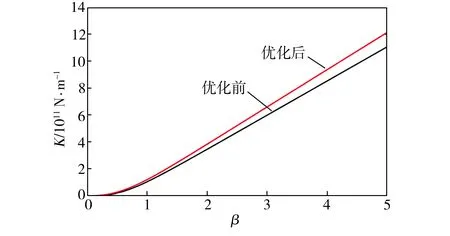
图7 优化前后液膜刚度K与宽长比β之间的关系
Fig.7RelationshipbetweenfilmstiffnessKandaspectratioβbeforeandafteroptimization
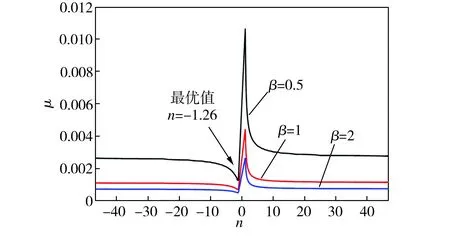
图8 β取值不同时摩擦因数μ和变量n之间的关系
Fig.8Relationshipbetweenfrictioncoefficientμandvariablenatdifferentβvalues

图9β=0.5时基于摩擦因数的滑移区/非滑移区最优拼接方案
Fig.9Optimalsplicingschemeofslip/no-slipzonebasedonfrictioncoefficientwhenβ=0.5
同理,β=0.5时液膜刚度最优值所对应的n=-25.34,如图10所示,与之对应的最优拼接方案如图11所示。与直线拼接相比,虽然这时滑移区/非滑移区拼接轨迹变化甚小,但是液膜刚度由优化前的2.0×1010N/m增至2.7×1010N/m。
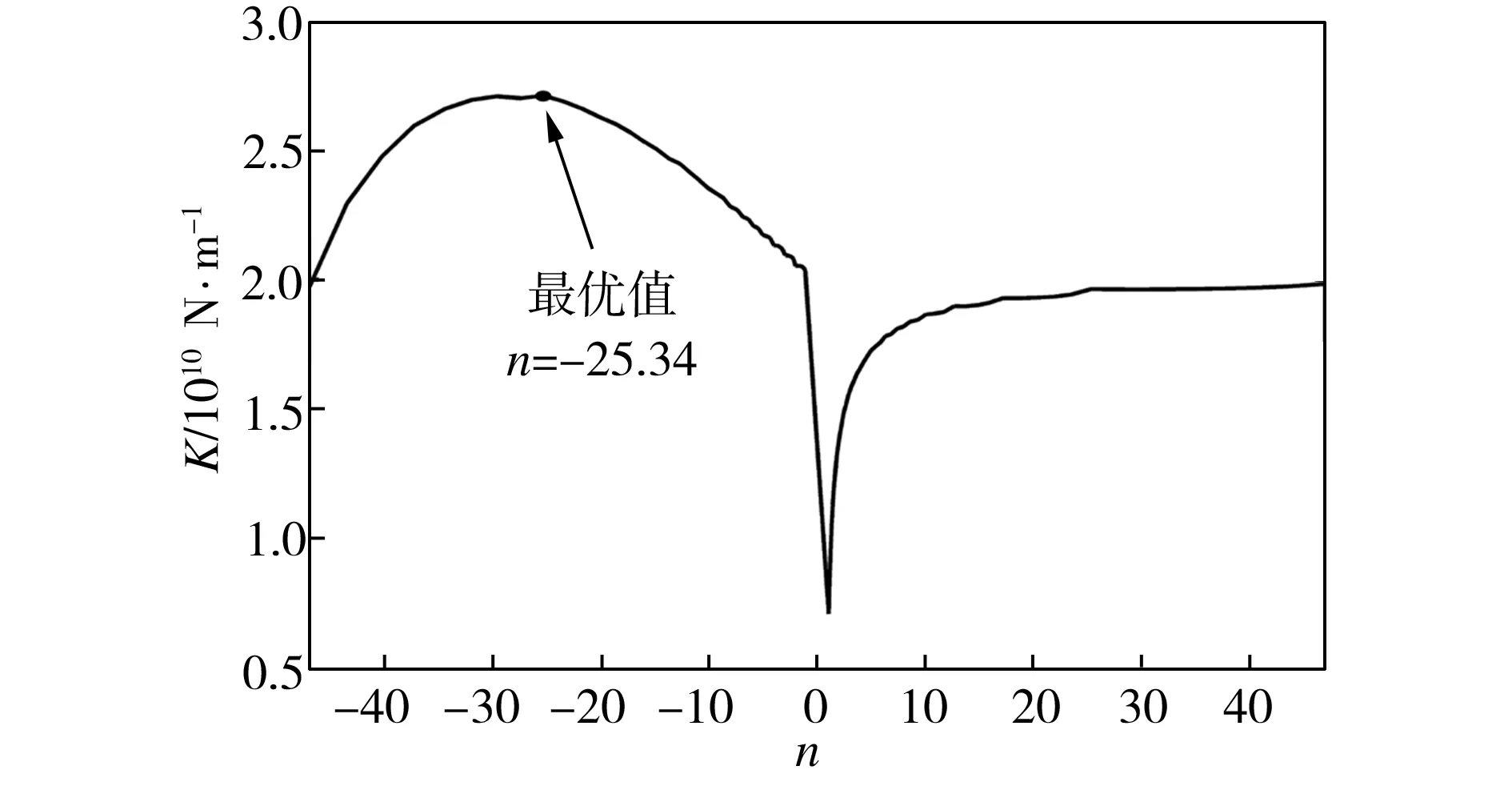
图10 β=0.5时液膜刚度K与变量n之间的关系
Fig.10RelationshipbetweenfilmstiffnessKandvariablenwhenβ=0.5
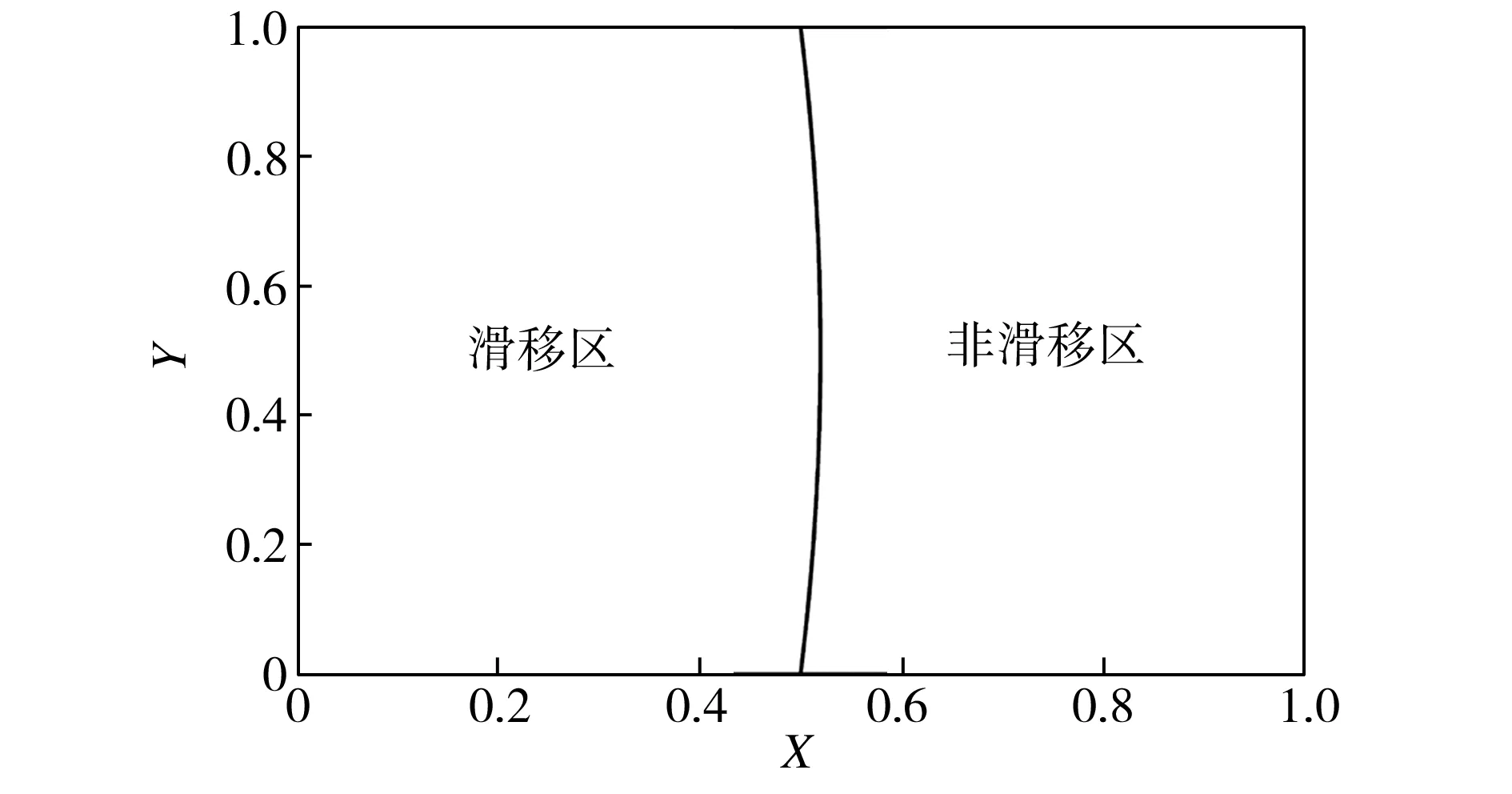
图11β=0.5时基于液膜刚度的滑移区/非滑移区最优拼接方案
Fig.11Optimalsplicingschemeofslip/no-slipzonebasedonfilmstiffnesswhenβ=0.5
对比图9和图11可以推断,根据不同的工况需求,对流体润滑摩擦副的性能要求不尽相同,因此优化目标就会各有侧重,从而导致优化后滑移区和非滑移区之间的拼接方案存在较大的差异。
3 结语
本文研究了滑移/非滑移异质界面动压润滑性能的优化,提出一种仅引入一个变量的离散式二次方程作为滑移区和非滑移区拼接轨迹的优化方法,针对现有流体润滑摩擦副的不同性能需求,以计算域宽长比为优化变量、分别以摩擦因数和液膜刚度为优化目标进行仿真求解。与现有的直线拼接方法相比,本文方法使流体润滑摩擦副的这两个优化指标均有所改善,针对具有任一宽长比的计算域和目标参数,都能绘制出对应的滑移区和非滑移区的最优拼接方案。
在后期研究中,可考虑将异质界面以单一或周期性分布的方式布置于摩擦副表面,并耦合楔形效应、空化效应等因素进行优化求解;也可以提高方程的阶数以增加样本数量;对于不同的优化对象,还可以采用三角方程、指数方程、椭圆方程等。针对液膜的动压生成区和空化区,本文方法可以进一步用于阶梯滑块以及表面织构形状的优化,通过引入方程中的一个或若干个变量带入程序中求解,以设计出更有针对性、性能更优异的流体润滑摩擦副。
参考文献
[1] Kalavathi G K, Dinesh P A, Gururajan K. Influence of roughness on porous finite journal bearing with heterogeneous slip/no-slip surface[J]. Tribology International, 2016, 102:174-181.
[2] Salant R F, Fortier A E. Numerical analysis of a slider bearing with a heterogeneous slip/no-slip surface[J]. Tribology Transactions, 2004, 47(3):328-334.
[3] Spikes H A. The half-wetted bearing (Part 1): extended Reynolds equation[J]. Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology, 2003, 217(1):1-14.
[4] AurelianF,PatrickM,MohamedH.Wallslipeffects in (elasto) hydrodynamic journal bearings[J].Tribology International, 2011, 44(7/8):868-877.
[5] Zhang H, Hua M, Dong G N, et al. Boundary slip surface design for high speed water lubricated journal bearings[J]. Tribology International, 2014, 79(11):32-41.
[6] 温诗铸,黄平.摩擦学原理[M]. 北京:清华大学出版社,2012.
[7] Cottin-Bizonne C, Barrat J L, Bocquet L, et al. Low-friction flows of liquid at nanopatterned interfaces[J]. Nature Materials, 2003, 2:237-240.
[8] 张颖,余广,曾良才,等.液压缸活塞微织构化表面动压润滑性能理论研究[J].武汉科技大学学报, 2017, 40(1):55-60.
[9] Srinivasan S, Kleingartner J A, Gilbert J B, et al. Sustainable drag reduction in turbulent Taylor-Couette flows by depositing sprayable superhydrophobic surfaces[J]. Physical Review Letters, 2015, 114(1):014501.
[10] 杨家友.水润滑轴承液膜刚度特性及对轴系振动的影响研究[D].哈尔滨:哈尔滨工程大学, 2013.

