模型参考自适应下的永磁同步电机无传感器矢量控制
韦汉培,魏海峰,张 懿
(江苏科技大学 电子信息学院, 镇江 212003)
永磁同步电机高性能控制如矢量控制以及直接转矩控制,都需要准确检测出转子实时位置、转速大小,工程中往往通过在电机转子上安装传感器来达到目的.但此方法增加系统成本以及体积,降低了系统可靠性,因此,需要去除机械传感器,提高系统可靠性并降低系统成本,同时又必须获得速度和磁链位置信号的无传感器控制方法.
目前适合永磁同步电机的最主要无传感器控制策略主要有一下几种:① 基于永磁同步电机磁链关系的转速和位置估算方法,此方法通过定子磁链的空间位置(计算反电势的位置)估算转速和转子位置,其计算简单,动态响应快,但对电机参数的准确性要求较高,应用时需结合电机参数的在线识别,并且在低速时,由于反电势值减小,这种方法较难准确估算[1-3];② 通过计算电感值估算转速和位置,只适用于具有凸极效应的永磁同步电机,且转子位置估算时间过长[4-6];③ 高频信号注入法,利用电机凸极效应,通过向电机定子绕组中注入高频信号从而估算出转子实际位置,这种方法受电机参数影响较小,但只适用于低速无传感器控制,对于无凸极效应的永磁同步电机(permanent magnet synchronous motor,PMSM)控制效果不是很好[7-10];④ 滑模观测器方法,此方法将状态观测器的控制回路修改成滑模变结构形式,滑模运动与控制对象的参数变化以及扰动无关,因此具有很好的鲁棒性,但是滑模变结构在本质上是不连续的开关控制,会引起系统发生抖动,对矢量控制在低速下运行是有害的,从而引起较大的转矩脉动[11-16];⑤ 模型参考自适应方法,该方法是一种基于基波励磁估算转子位置和速度的方法,能保证参数估计的渐进收敛,具有良好的动态性能[17-18].
文中采用模型参考自适应(model reference adaptive system,MRAS)算法对永磁同步电机转子速度以及位置进行辨识,基于该算法搭建永磁同步电机无传感器矢量控制仿真模型,控制实验平台,仿真以及实验结果表明MRAS算法可准确估算出电机转子速度以及位置,适用于永磁同步电机无传感器矢量控制.
1 模型参考自适应思想
模型参考自适应法以角速度为可调参数构建电机可调模型,再加入与电机同等的激励(电压),解算出电机输出(电流),与实际检测到的电流相比较,通过一定自适应率调节参考模型可调参数,使得可调模型输出量接近实际电机对应参数,此时的可调参数值即可被认为是该变量的实际值.参考模型为不含未知参数的方程,可调模型为含有待估参数(如转速)的方程,两个模型既有相同的物理意义输出量,又同时工作.此时利用输出的误差构成合适自适应律实时调节可调模型参数,从而使得可调模型输出能够准确跟踪参考模型输出.因此,MRAS控制系统本质为参考模型与可调模型误差的调整过程,其基本原理如图1.

图1 MRAS基本结构Fig.1 Basic structure of MRAS

2 模型参考自适应下的矢量控制
2.1 参考模型和可调模型确定
永磁同步电机在d-q轴坐标系下的定子电流数学模型为:

(1)
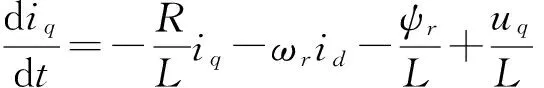
(2)
根据以上两式,永磁同步电机d-q轴坐标系下的定子电流数学模型只与其转速相关,故选电流模型作为可调模型,永磁同步电机本身作为参考模型,采用并联结构进行转速识别.为便于分析系统稳定性,使转速量约束于系统状态矩阵,对上两式中控制量和状态变量做相应的变化可得:
(3)
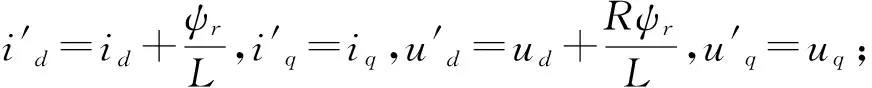
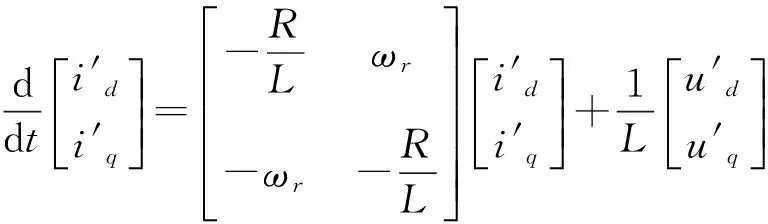
(4)
可以化简为如下形式:

(5)
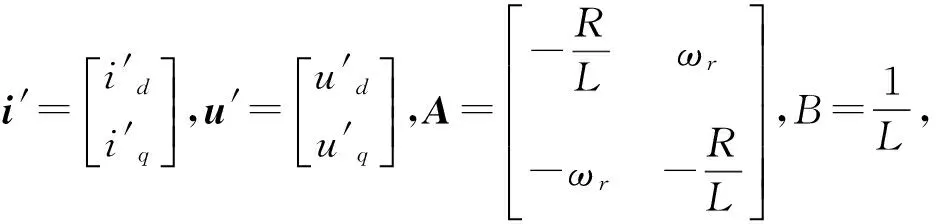
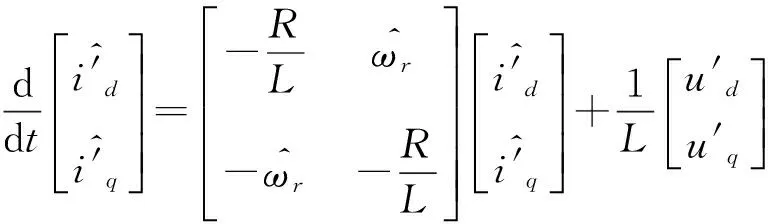
(6)
同理,可以简化为如下形式:
(7)
将式(4)减去式(6),可得:
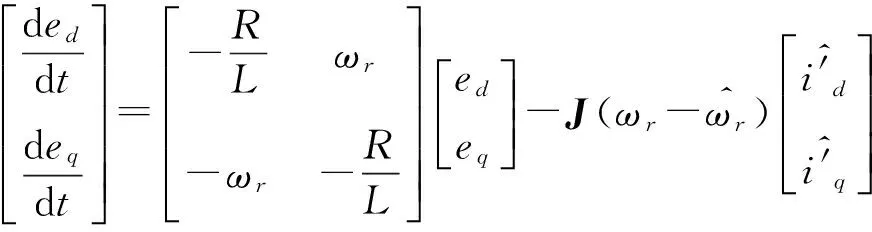
(8)

式(8)可简化为如下形式:
(9)
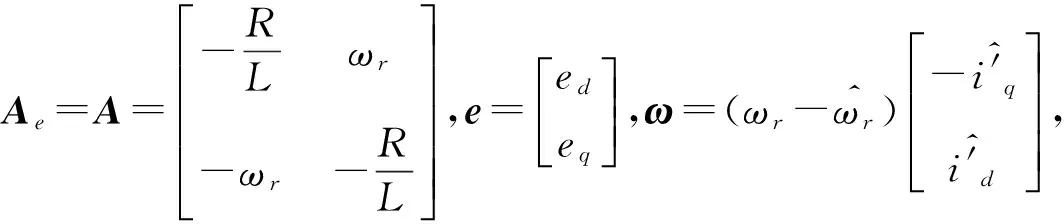
式(9)为定子电流矢量误差方程,由此可以得到一个标准的反馈系统,如图2.
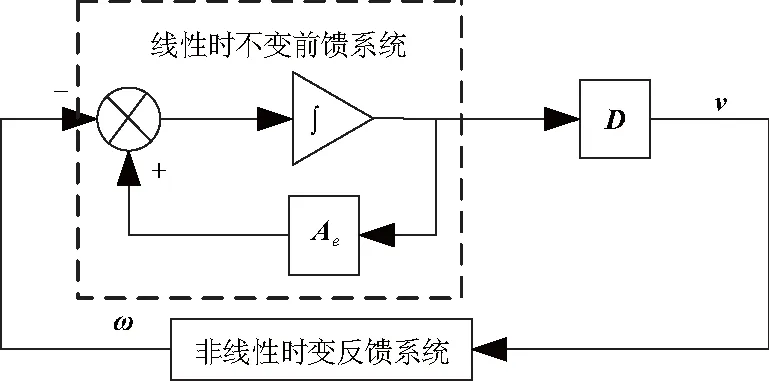
图2 等效非线性反馈系统Fig.2 Equivalent non-linear feedback system
2.2 自适应律确定
为了构建性能优良的MRAS算法,必须确定合适的自适应律,自适应律一般选择比例加积分的形式.设计合适的自适应律需要寻找到自适应量v和反馈量ω间的关系.这里用一个非线性时变反馈系统表示其关系.基于Popov超稳定性理论设计的模型参考自适应系统不仅可以使可调模型逼近参考模型,还可以保证系统稳定性.因此根据Popov超稳定性定理,如果满足:
(1) 非线性式变环节满足Popov积分不等式:
(10)
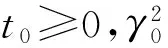
(2) 传递阵H(s)=D(sI-A)-1.
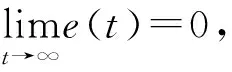
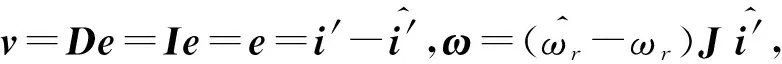
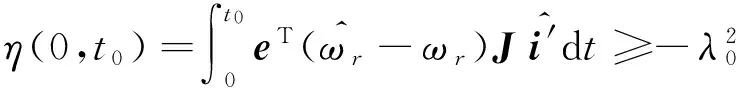
(11)
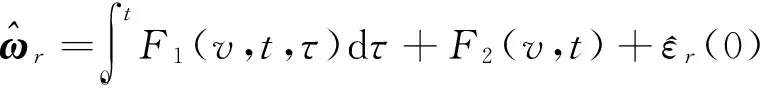
(12)
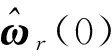
η(0,t0)=
(13)

η1(0,t0)=
(14)
(15)

对于式(14)可以利用不等式(16),即
(16)
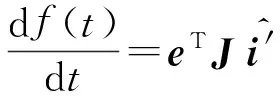
(17)
(18)
对式(18)两边求导可得:
(19)

对于式(15),如果不等式左边被积函数为正,则不等式一定满足,因此可以取
(20)
显然,将式(19)和式(20)代入式(13),一定会满足Popov积分不等式,即
η(0,t0)=
(21)
反之,证明式(12)成立,即
(22)
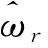

(23)
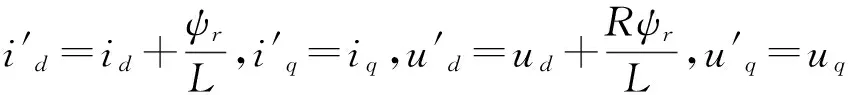
(24)

2.3 基于MRAS的无速度传感器矢量控制
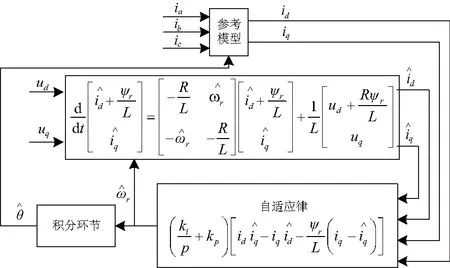
图3 MRAS算法速度辨识Fig.3 Speed identification of MRAS
3 仿真分析
文中采用MATLAB验证MARS算法的有效性,搭建基于此算法的永磁同步电机无传感器矢量控制仿真平台.其中,采用永磁同步电机参数如下:额定功率为1.2 kW,额定电压为110 V,额定转速为1 200 r/min,极对数为2,交、直轴电感均为15.3 mH,定子电阻为0.56 Ω.其仿真原理如图4.
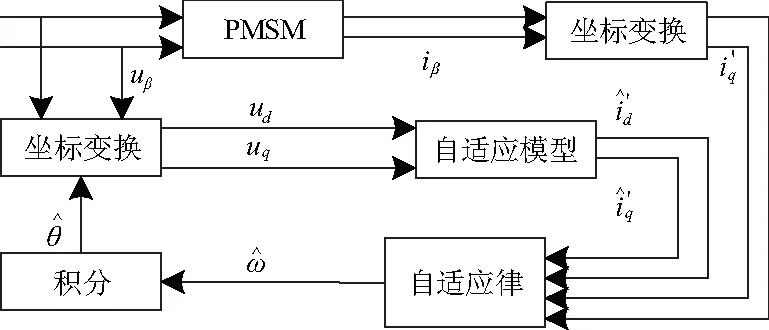
图4 无传感器矢量控制模型参考自适应转速估计系统Fig.4 Speed estimation for sensorless vector controlmodel based on MRAS
3.1 电机启动
电机启动阶段,电机的估计转速以及实际转速曲线如图5.对比两种曲线可以看出,在电机启动阶段,MRAS算法可以很好地估算电机转速,估计的转速可以很好地跟踪电机实际转速,系统大概需要0.07 s的时间达到稳态.
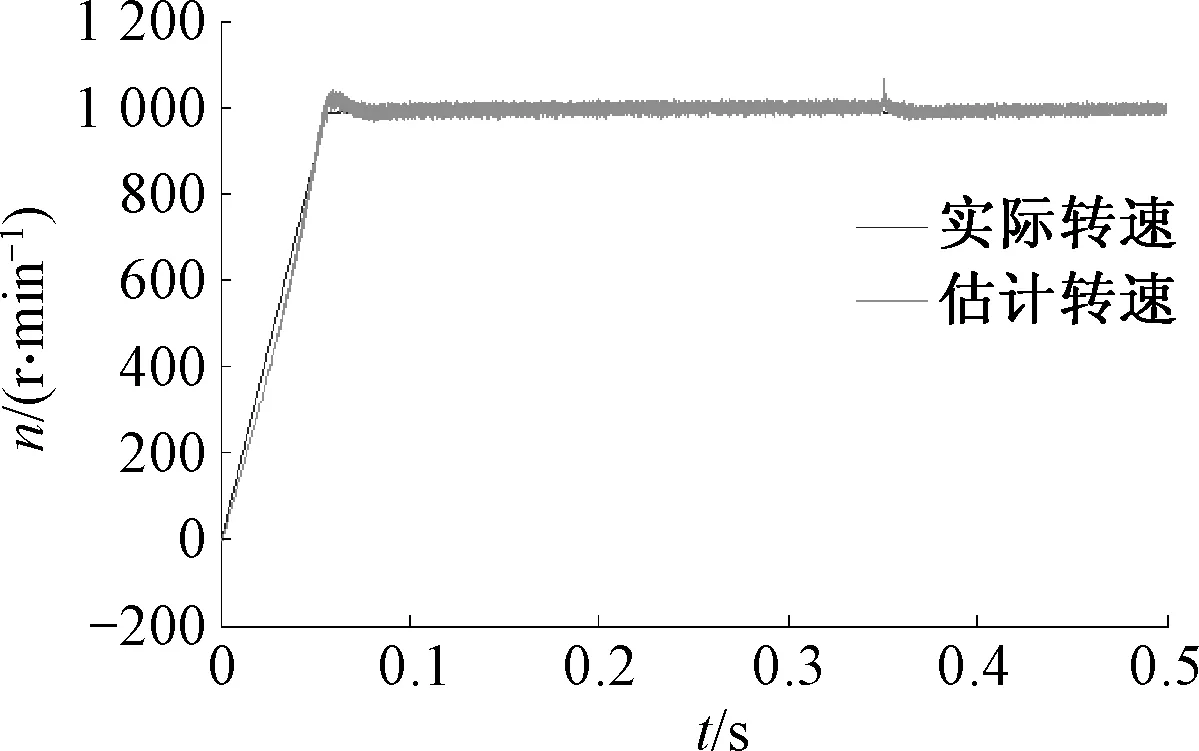
图5 电机启动阶段估计转速与实际转速对比Fig.5 Estimated speed and actual speed comparisonchat in motor start
3.2 转速突变
在0.25 s将给定转速由1 000 r/min变为1 500 r/min,如图6,可以看出,估计的转速可以很好地跟踪电机实际转速,估算精度基本可以满足矢量控制系统要求.在电机启动阶段和速度突变阶段转速估算误差较大,但是在MRAS算法作用下的误差很快得到收敛,且未出现较大的转速脉动情况,系统能够很快达到新的稳定状态,仿真效果较好.
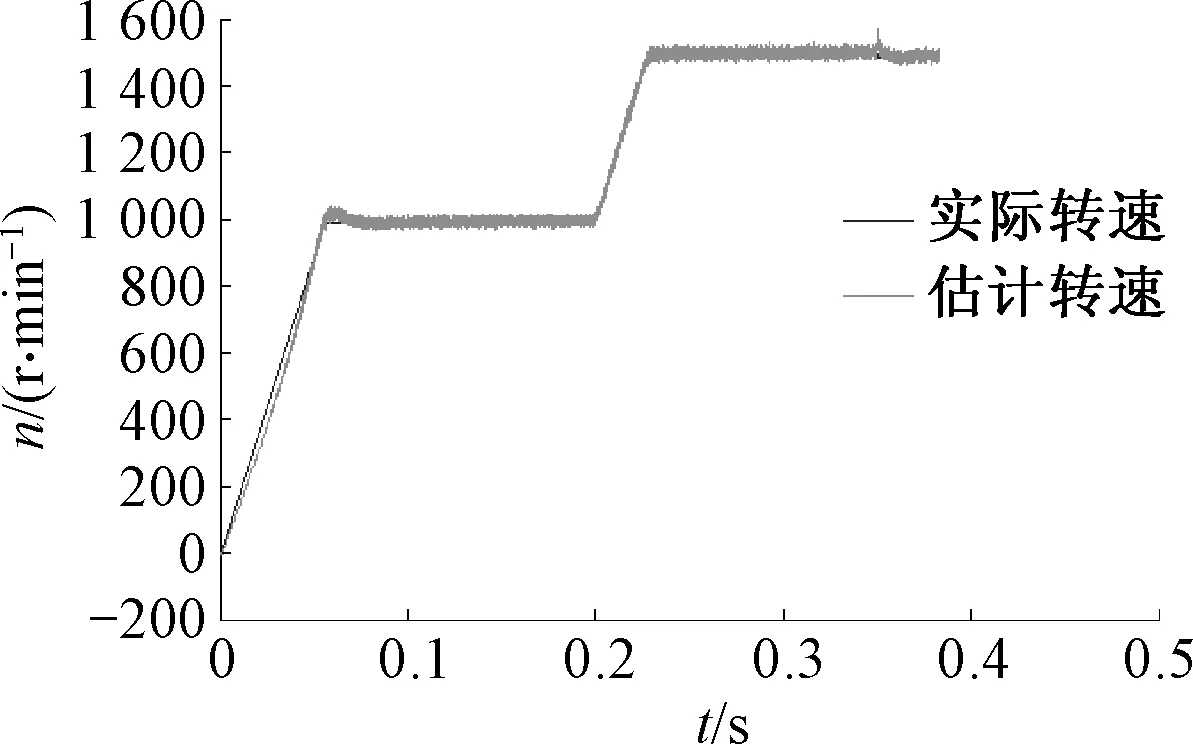
图6 转速突变时估计转速与实际转速对比Fig.6 Estimated speed and actual speed comparisonchat when speed changes
转速突变下的电机输出电磁转矩如图7,仿真中外加输入负载转矩为1 N·m,所以从图中看出电机的输出电磁转矩也约为1 N·m.由于在0.25 s时给定转速发生变化,所以出现较大的转矩脉动.
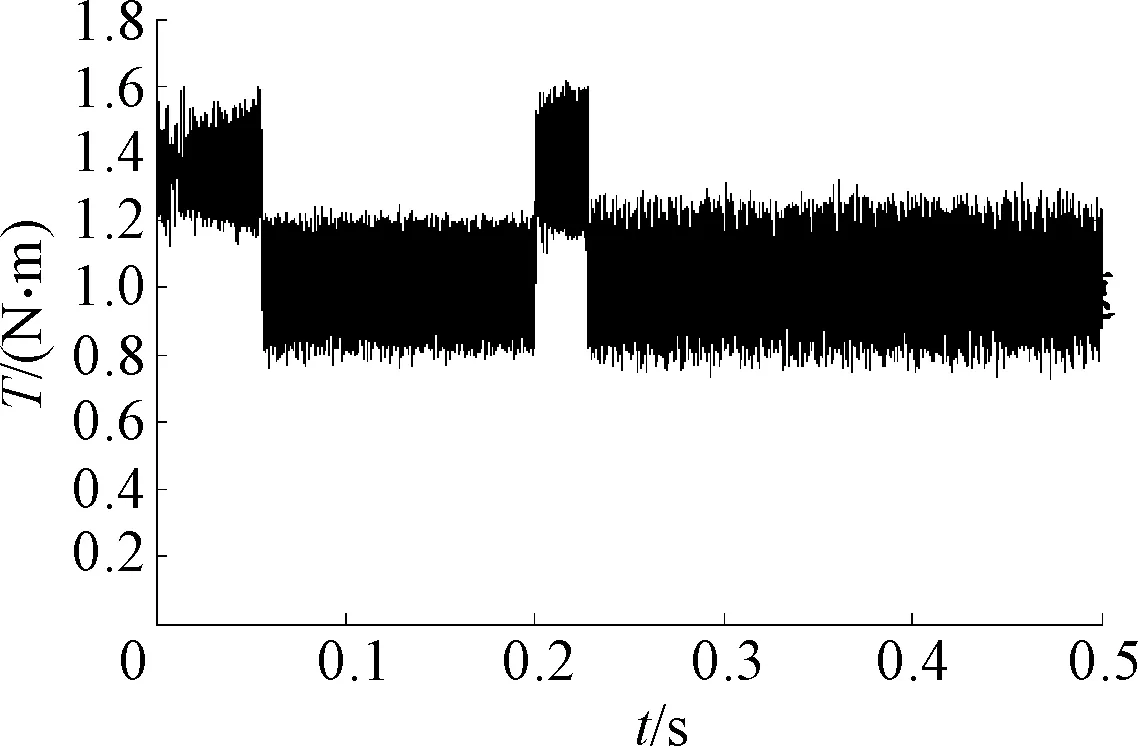
图7 转速突变时电机输出电磁转矩Fig.7 Motor output torque when speed changes
转速突变下电机定子三相电流波形如图8,从图中可以看出,每相电流基本为正弦波,这说明在基于MRAS算法的无传感器矢量控制策略下,永磁同步电机能够正常稳定地旋转.在0.25 s转速突变时电流会有一定的波动.

图8 转速突变时电机定子电流波形Fig.8 Current waveform of motor statorwhen speed changes
矢量控制需要准确知道电机转子的实际位置,图9为MRAS算法估算出的转子位置与实际位置对比图,可以看出该算法下的估算转子位置能够精确实时跟随实际转子位置,适用于永磁同步电机无传感器矢量控制.
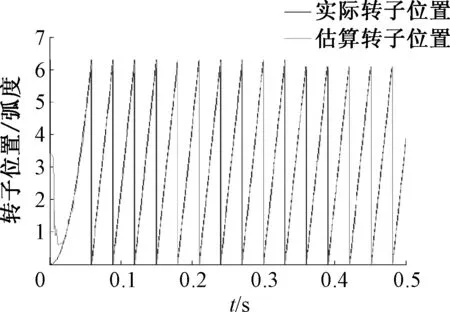
图9 转速突变时估计转子位置与实际转子位置对比Fig.9 Estimated rotor position and actual rotor positioncomparison chat when speed changes
3.3 负载转矩突变
图10为电机负载转矩突变时的电机估计转速以及实际转速对比图,在0.35 s将负载转矩由1 N·M变为2 N·M,但从图中可看出负载转矩的突变对估计转速以及实际转速都基本不产生影响.
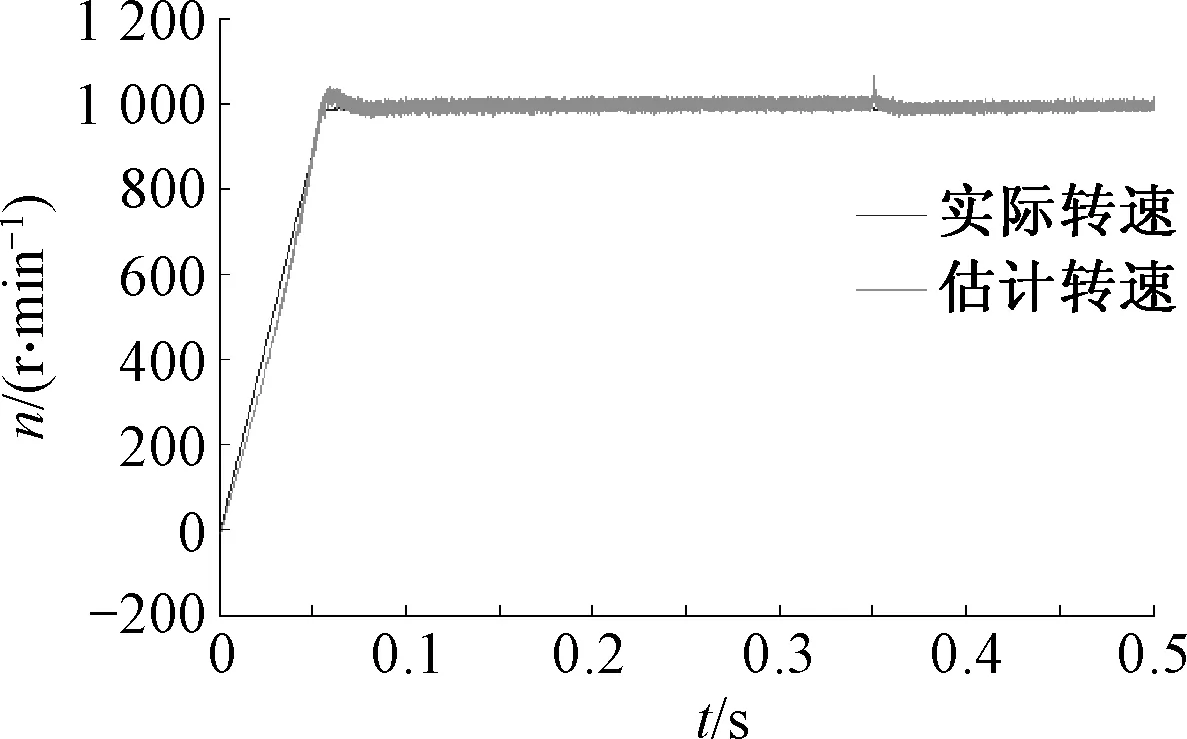
图10 负载转矩突变时估计转速与实际转速对比Fig.10 Estimated speed and actual speed comparisonchar when load torque changes
当负载转矩突变时,永磁同步电机三相定子电流波形如图11,在给定负载转矩成倍增大时,三相电流幅值也成倍增大.
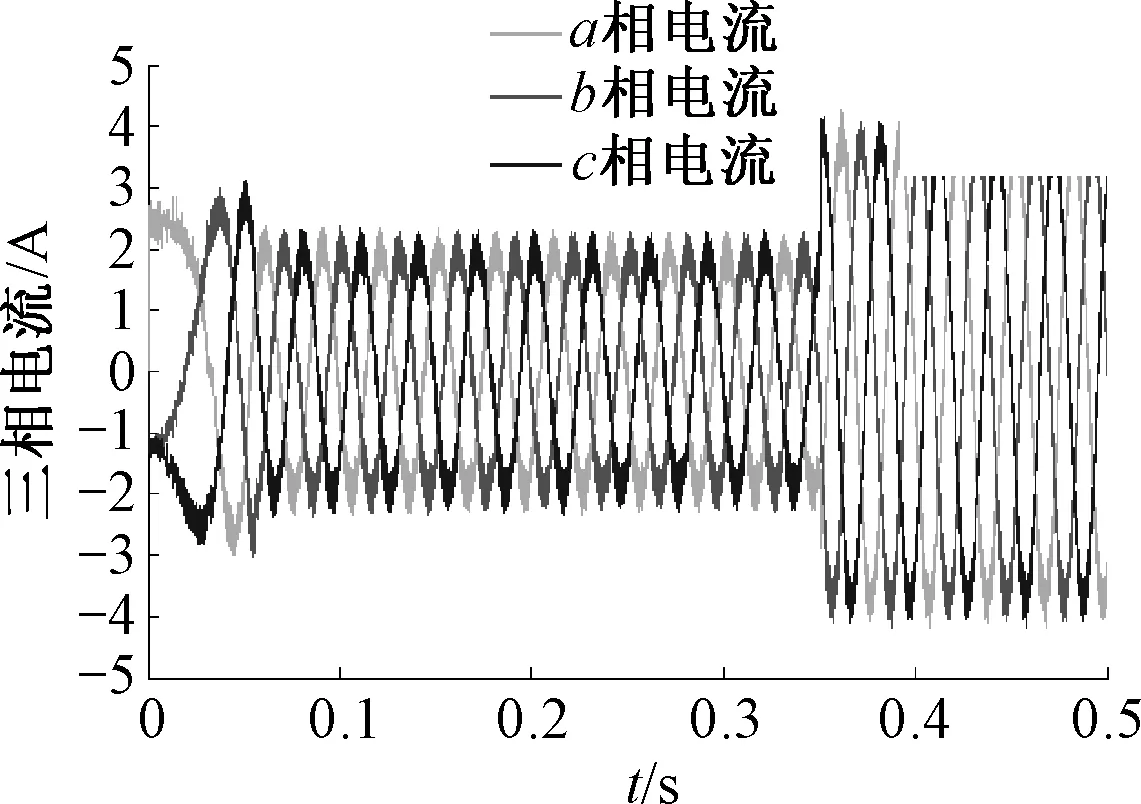
图11 负载转矩突变时电机定子电流波形Fig.11 Current waveform of motor statorwhen load torque changes
图12为负载突变时电机输出电磁转矩响应,由图可看出电机实际输出电磁转矩能够很好地跟随负载给定.
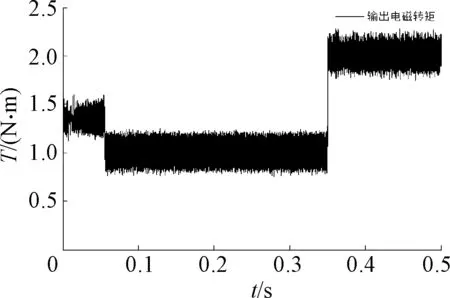
图12 负载突变时电机输出电磁转矩Fig.12 Motor output torque when load torque changes
4 实验分析
为了进一步验证MRAS算法有效性,采用TMS320F2812控制芯片的永磁同步电机交流调速实验平台,编写基于MRAS算法的永磁同步电机无传感器矢量控制程序,基于Visual Basic 2010编写虚拟示波器对永磁同步电机运行过程中转子估算位置以及转速估算波形实时对比.实验采用江苏科技大学罗克韦尔实验室中的750 W永磁同步电机,其参数如表1.

表1 表贴式永磁同步电机参数Table 1 Surface mounted permanent magnetsynchronous motor parameters
如图13为给定永磁同步电机1 200 r/min转速下的永磁同步电机高速启动阶段的估计转速与实际转速对比,可以明显看出,电机响应速度快,估计转速能够较快得跟踪给定值,且估算转子位置误差不明显,抖动小,启动特性良好.

图13 电机高速启动阶段估计转速与估计转子位置误差Fig.13 Estimated speed and estimated rotor positionerror in motor start of high speed
图14为给定永磁同步电机400 r/min低转速下的永磁同步电机启动阶段的估计转速与实际转速对比,可以明显看出,电机响应速度快,估计转速能够实时跟踪实际转速,误差不明显,低速性能较好.

图14 电机低速启动阶段估计转速与实际转速对比Fig.14 Comparison of estimated speed and actual speedin motor start of low speed
图15为额定负载转矩下给定转速突变工况的轴估算转速和估算位置角误差响应,电机稳定运行于1 000 r/min,经过一段时间给定电机转速由1 000 r/min突变为120 r/min,继而给定转速由120 r/min突变为800 r/min.由图15,MRAS算法下的电机转速响应迅速,给定转速突变对电机估算转子位置无显著影响,转速动态响应性能优良.
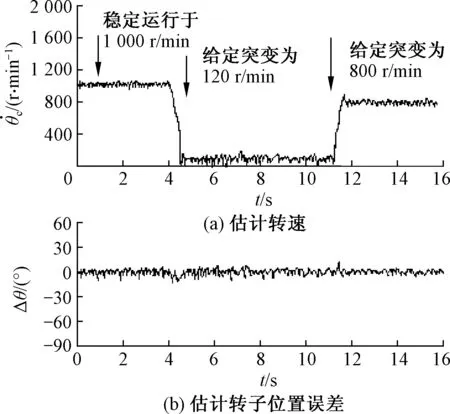
图15 给定转速突变下的估计转速与估计转子位置误差Fig.15 Estimated speed and estimated rotor postitionerror under given speed change
图16给出电机实际转子位置角θ与MRAS控制算法下的估算转子位置角θc对比曲线,其中给定转速为200 r/min.由图可看出MRAS控制算法下的估算电机转子位置基本可以达到零误差跟踪实际转子位置的水平,低速运行特性良好.

图16 转速突变时估计转子位置与实际转子位置对比Fig.16 Estimated rotor position and actual rotor positioncomparison chat when speed changes
图17(a、b)和(c、b)分别表示突加和突减额定负载工况下的电机旋转交轴电流和转子位置估算误差Δθ的响应曲线.电机转矩电流对于负载突变情况具有较迅速的响应能力,估算转子位置误差变化小,系统稳定性强,表明MRAS算法对控制系统外部扰动具有较强鲁棒性,且电机转矩电流脉动小,转子位置角度估算准确.
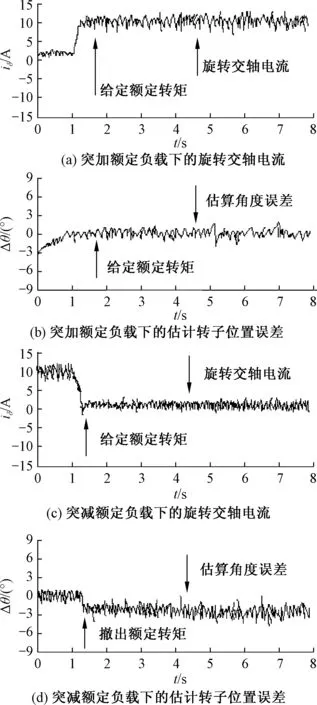
图17 负载突变下的旋转交轴电流和估算位置角误差响应Fig.17 Response of rotating AC axis current and rotorposition error under the sudden change of load
5 结论
文中将模型参考自适应算法用于永磁同步电机无传感器矢量控制中的转子速度以及位置估算,从理论、仿真以及实验三方面分析研究,结果表明:
(1) MARS算法对于永磁同步电机的启动、转速突变以及负载转矩突变情况有较好的适应性.
(2) 文中设计的基于MRAS的无传感器矢量控制系统可以较为准确地观测出永磁同步电机转速以及转子位置,具有较好的控制性能,实现永磁同步电机的无传感器控制.
(3) 基于模型参考自适应算法所设计的永磁同步电机无传感器控制系统可以很好地取代光电编码器,极大地提高了系统可靠性,并降低了成本.
参考文献(References)
[ 1 ] 方晓春, 原佳亮, 赵冬, 等. 基于永磁同步电机定子磁链轨迹跟踪的中间同步调制动态性能优化[J]. 电工技术学报, 2015, 30(10): 108-114.
FANG Xiaochun, YUAN Jianliang, ZHAO Dong. The central synchronous modulation based on permanent magnet synchronous motor stator flux trajectory control[J]. Transactions of China Electro technical Society, 2015, 30(10): 108-114. (in Chinese)
[ 2 ] 史宇超, 孙凯, 马鸿雁, 等. 内埋式永磁同步电机永磁磁链的在线辨识[J]. 电工技术学报, 2011, 26(9): 48-53.
SHI Yuchao, SUN Kai, MA Hongyan, et al. On-line identification of permanent magnet flux in IPMSM drive[J]. Transactions of China Electro technical Society, 2011, 26(9): 48-53. (in Chinese)
[ 3 ] 邱腾飞, 温旭辉, 赵峰, 等. 永磁同步电机永磁磁链自适应观测器设计方法[J]. 中国电机工程学报, 2015, 35(9): 2287-2294.
QIU Tengfei, WEN Xuhui, ZHAO Feng, et al. Design strategy of permanent magnet flux linkage adaptive observer for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2015, 35(9): 2287-2294. (in Chinese)
[ 4 ] 刘金海, 陈为, 胡金高. 永磁同步电机dq电感参数新实验获取法[J]. 电工技术学报, 2014, 29(7): 97-103.
LIU Jinhai, CHEN Wei, HU Jingao. Novel experiment methods of acquiring dq inductance permanent magnet synchronous motors[J].Transactions of China Electro-technical Society,2014,29(7):97-103.(in Chinese)
[ 5 ] 符荣, 窦满峰. 电动汽车驱动用内置式永磁同步电机直交轴电感参数计算与实验研究[J]. 电工技术学报, 2014, 29(11): 30-37.
FU Rong, DOU Manfeng. D-axis and Q-axis inductance calculation and experimental research on interior permanent magnet synchronous motors for EV[J]. Transactions of China Electrotechnical Society,2014,29(11):30-37.(in Chinese)
[ 6 ] 程树康, 于艳君, 柴凤. 内置式永磁同步电机电感参数的研究[J]. 中国电机工程学报, 2009, 29(18): 94-99.
CHENG Shukang, YU Yanjun, CHAI Feng. Analysis of the inductances of interiors permanent magnet synchronous motor[J]. Proceeding of the CSEE, 2009, 29(18): 94-99. (in Chinese)
[ 7 ] 周晓敏, 王长松, 钟黎萍. 基于卡尔曼滤波和高频信号注入的永磁同步电机转子位置自检测[J]. 北京科技大学学报, 2008, 30(7): 815-819.
ZHOU Xiaomin, WANG Changsong, ZHONG Liping. Rotor position self-sensing of a sensorless permanent synchronous motor based on fluctuating high-frequency voltage signal injection and Kalman filter[J]. Journal of University of Science and Technology Beijing, 2008, 30(7): 815-819. (in Chinese)
[ 8 ] 朱昊, 肖曦, 李永东. 永磁同步电机高频信号注入法启动过程可靠性研究[J]. 清华大学学报(自然科学版), 2010, 50(10): 1637-1645.
ZHU Hao, XIAO Xi, LI Yongdong. Reliable starting of high frequency injection permanent magnet synchronous motor control[J]. Journal of Tsinghua University(Science and Technology),2010,50(10):1637-1645.
[ 9 ] 金光哲, 徐殿国, 高强, 等. 高频注入电压预估同步电机转子位置检测方法[J]. 中国电机工程学报, 2014, 34(9): 1376-1383.
JIN Guangzhe,XU Dianguo,GAO Qiang,et al.A synchronous motor rotor position detection method based on high-frequency injection voltage predictionA[J].Proceeding of the CSEE,2014,34(9):1376-1383.(in Chinese)
[10] 万山明, 吴芳, 黄声华. 基于高频电压信号注入的永磁同步电机转子初始位置估计[J]. 中国电机工程学报, 2008, 28(33): 82-86.
WAN Shanming, WU Fang, HUANG Shenghua. Initial rotor position estimation of permanent magnet synchronous motor based on high frequency voltage signal injection method[J]. Proceeding of the CSEE, 2008, 28(33): 82-86. (in Chinese)
[11] LU W,HU Y,HUANG W,et al.Sensorless control of permanent magnet synchronous machine based on a novel sliding mode observer[C]∥Vehicle Power and Propulsion Conference,2008.Harbin,China:IEEE,2008:1-4.
[12] 张晓光, 孙力, 陈小龙, 等. 基于二阶滑模观测器的永磁同步电机无位置传感器控制[J]. 电力自动化设备, 2013, 33(8): 36-41.
ZHANG Xiaoguang, SUN Li, CHEN Xiaolong, et al. The sensorless control of PMSM based on the second-order synovial observer[J]. Electric Power Automation Equipment, 2013, 33(8): 36-41. (in Chinese)
[13] 张晓光, 赵克, 孙力. 永磁同步电机混合非奇异终端滑模变结构控制[J]. 中国电机工程学报, 2011, 31(27): 116-122.
ZHANG Xiaoguang, ZHAO Ke, SUN Li. Hybrid nonsingular terminal sliding mode control for permanent magnet synchronous motor drive system[J].Proceedings of the CSEE,2011,31(27):116-122.(in Chinese)
[14] 丁文, 梁得亮, 罗战强. 两级滤波滑模观测器的永磁同步电机无位置传感器控制[J]. 电机与控制学报, 2012, 16(11): 1-10.
DING Wen, LIANG Deliang, LUO Zhanqiang. Position sensorless control of PMSM using sliding mode observer with two-stage filter[J]. Electric Machines and Control, 2012, 16(11): 1-10. (in Chinese)
[15] KANG K L, KIM J M, HWANG K B. Sensorless control of PMSM in high speed range with itertive sliding mode observer[C]//Applied Power Electronics Conference and Exposition. Anaheim, USA: IEEE, 2004: 1111-1116.
[16] 张晓光, 赵克, 孙力, 等. 永磁同步电机滑模变结构调速系统动态品质控制[J]. 中国电机工程学报, 2011, 31(15): 47-52.
ZHANG Xiaoguang, ZHAO Ke, SUN Li, et al. Sliding mode control of permanent magnet synchronous motor based on a novel exponential reaching law[J].Proceedings of the CSEE,2011,31(15):47-52.(in Chinese)
[17] 敬华兵, 廖力清. 基于模型参考自适应方法的无速度传感器永磁同步电机控制[J]. 机车电传动, 2007 (1): 33-36.
JING Huabing, LIAO Liqing. Control of speed sensorless permanent magnet synchronous motor based on MRAS[J]. Electric Drive for Locomotives, 2007, (1): 33-36. (in Chinese)
[18] 王庆龙,张兴,张崇巍.永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J]. 中国电机工程学报, 2014, 34(6): 897-902.
WANG Qinglong, ZHANG Xing, ZHANG Chongwei. Double sliding-mode model reference adaptive system speed identification for vector control of permanent magnet synchronous motors[J]. Proceeding of the CSEE, 2014, 34(6): 897-902.(in Chinese)

