剪式单元阵列可展结构的动力学分析方法

彭麒安， 王三民， 智常建， 李 博

(西北工业大学 机电学院，西安 710072)

可展结构是一种能够像机构一样运动，又能在锁定后承受载荷、保持稳定构型的结构。与目前常见的其他结构不同的是，可展结构一般是由某一特定单元进行一定规则阵列组合而成，这是其区别于其他结构的显著特点。随着可展结构应用越来越广泛，引发了许多学者的研究兴趣。文献[1-7]设计了各种新类型的可展结构，文献[8-11]研究了可展结构作为机构时的运动学和动力学特性，文献[12-15]则对其作为结构时静力学问题进行了分析。文献[16]虽然研究了可展结构的固有频率，但使用的是传统有限元方法，很难向大型阵列可展结构推广。

随着可展结构在航天领域深入应用，对其稳定性和振动要求越发严格，所以结构动力学成为了可展结构新的研究重点。但因其阵列单元数目过于庞大，难以用传统有限元动力学分析方法进行分析，所以急需一种能够快速简单建立起动力学模型的方法。

本文以剪式单元平面阵列可展结构为研究对象，将通过对其单元特性矩阵进行规范化处理，使其叠加节点自由度与内部节点自由度分开，从而实现通过单元特性矩阵的首尾循环相加来获得整体结构的刚度矩阵和质量矩阵，以提高建模效率，同时便于编程计算，并以此为基础对可展结构进行动力学的分析，研究其固有频率和动态响应等特性。因可展结构大部分具有阵列特性，故此方法也可推广到其他单元类型的可展结构中。

1 剪式单元机构动力学模型与方程

剪式单元平面阵列可展结构如图1 所示，可以看出它是由M层剪式单元线状阵列可展结构拼接而成，而每层剪式单元线状阵列又是由N个平面剪式单元可展结构组成，本文先对单个剪式单元进行研究，然后通过一定的方法进行组合最终得到复杂剪式单元面状可展结构的相关特性。

图1 剪式单元平面阵列可展结构

单个剪式单元机构如图2所示，它是由两个杆通过中间枢轴节点铰接在一起的一个可展结构，展开角度用α表示。

一个剪式单元机构是由6个节点构成，分别为1,2,3,3′,4,5，其中3,3′是两杆上各自的铰接点，1,5和2,4分别是杆1和杆2两端的端节点同时也是与外界相连的铰节点。由于剪式单元的力学特性，在有限元分析中选用两节点六自由度的梁单元进行分析，故此将剪式单元划分成4个梁单元，分别为13,35,23′,3′4。

图2 剪式单元机构

由有限元理论可知梁单元的质量矩阵和刚度矩阵分别为Me和Ke，坐标变换后利用主从自由度法约束铰节点3,3′可得到剪式单元真实力学模型为

(1)

式中：Mr和Kr分别为剪式单元的质量矩阵和刚度矩阵;Cr为阻尼矩阵，在本文中均采用Rayleigh黏性比例阻尼模型;Pr为与时间相关的外载列阵。

2 阵列可展结构动力学分析方法

以图2为例，剪式单元可展结构的节点位移为q=[u1,v1,θ1,u2,v2,θ2,u3,v3,θ3,θ3′,u4,v4,θ4,u5,v5,θ5]T，为了能够实现前后两个单元刚度矩阵和质量矩阵首尾相加，让独立的自由度不影响主从约束自由度的叠加，将节点位移列阵进行规范化

q′=Pq

(2)

式中:P为规范矩阵，规范化后的位移列阵为q′=[u1,v1,u2,v2,θ1,θ2,u3,v3,θ3,θ3′,θ4,θ5,u4,v4,u5,v5]T利用滤波法求解变换矩阵P，先假设变换矩阵P是一个全一矩阵，即为

现设置约束条件集为

(3)

式中i,j=1,2,3，…，16。

将其代入式(2)，则可以得到变换矩阵为P。得到变换矩阵后，即可求出变换过后的刚度矩阵为

KP=P·K·PT

(4)

再将其进行(N-1)次加法运算即可得到剪式单元线状可展结构的刚度矩阵

式中：KH=Kaa+Kcc，Kaa和Kcc为叠加节点自由度对应的刚度矩阵;Kbb为内部节点自由度对应的刚度矩阵，其余矩阵为叠加节点自由度和内部节点自由度对应的耦合刚度矩阵。同理也可得质量矩阵MX。

再以剪式单元线状阵列可展结构为子结构单元，进行规范化处理，N个剪式单元的线阵列可展结构节点位移列阵为

(5)

式中：i=0,1,2…n,j=1,2,…n。

(6)

由此将其进行(M-1)次加法运算得到剪式单元面状可展结构的刚度矩阵KM和质量矩阵MM。

故剪式单元平面阵列可展结构的动力学方程为

(7)

式中：MM、CM、KM、FM、qM分别为剪式单元平面阵列可展结构的质量矩阵、阻尼矩阵、刚度矩阵、与时间相关的广义力向量和广义位移向量。

因为可展结构在展开过程中应该避免发生共振，所以首先对其进行模态分析有

(8)

考虑到在工作状态时，可展结构会受到变化的外载，对可展结构造成影响，因此还应该研究此时结构的动态响应

(9)

式中：MB,CB,KB,FB,qB分别为约束为结构后的平面阵列可展结构的质量矩阵、阻尼矩阵、刚度矩阵、与时间相关的外载列阵和位移列阵。

3 算 例

下面分析一个5×5的平面阵列可展结构的结构动力学，剪式单元个数N×M=25，杆件长度l=50 mm，横截面宽b=3 mm，横截面高h=4 mm，材料为空间中常用的铝合金，其弹性模量E=71 GPa，密度ρ=2 770 kg/m3。根据以上条件求其动力学方程：由文献[17]可知，按照传统有限元方法需要对剪式单元的特性矩阵进行528次基本运算才能得到平面阵列剪式可展结构的特性矩阵；而按照本文方法只需对规范化后的矩阵进行16次加法运算就能得到可展结构的特性矩阵，运算次数仅为传统方法的1/33，由此看来本文的规范法能够大大提高建模效率。

3.1 模态分析

展开角度α=60°，通过编程得到固有频率计算结果以及用ANSYS仿真计算结果(前12阶)，将仿真计算结果作为标准，如表1所示。

表1 计算值与仿真值对比

从表1可以看出，无论是计算值还是仿真值前四阶固有频率都等于0，这是因为自由振动时，平面可展结构具有本身三个方向的刚体位移和一个运动的自由度导致的；另一方面，计算值与仿真值的最大误差不超过0.04%，可以证明规范化方法的正确性。

依次计算展开角度α=0°～180°的固有频率，结果如图3所示。

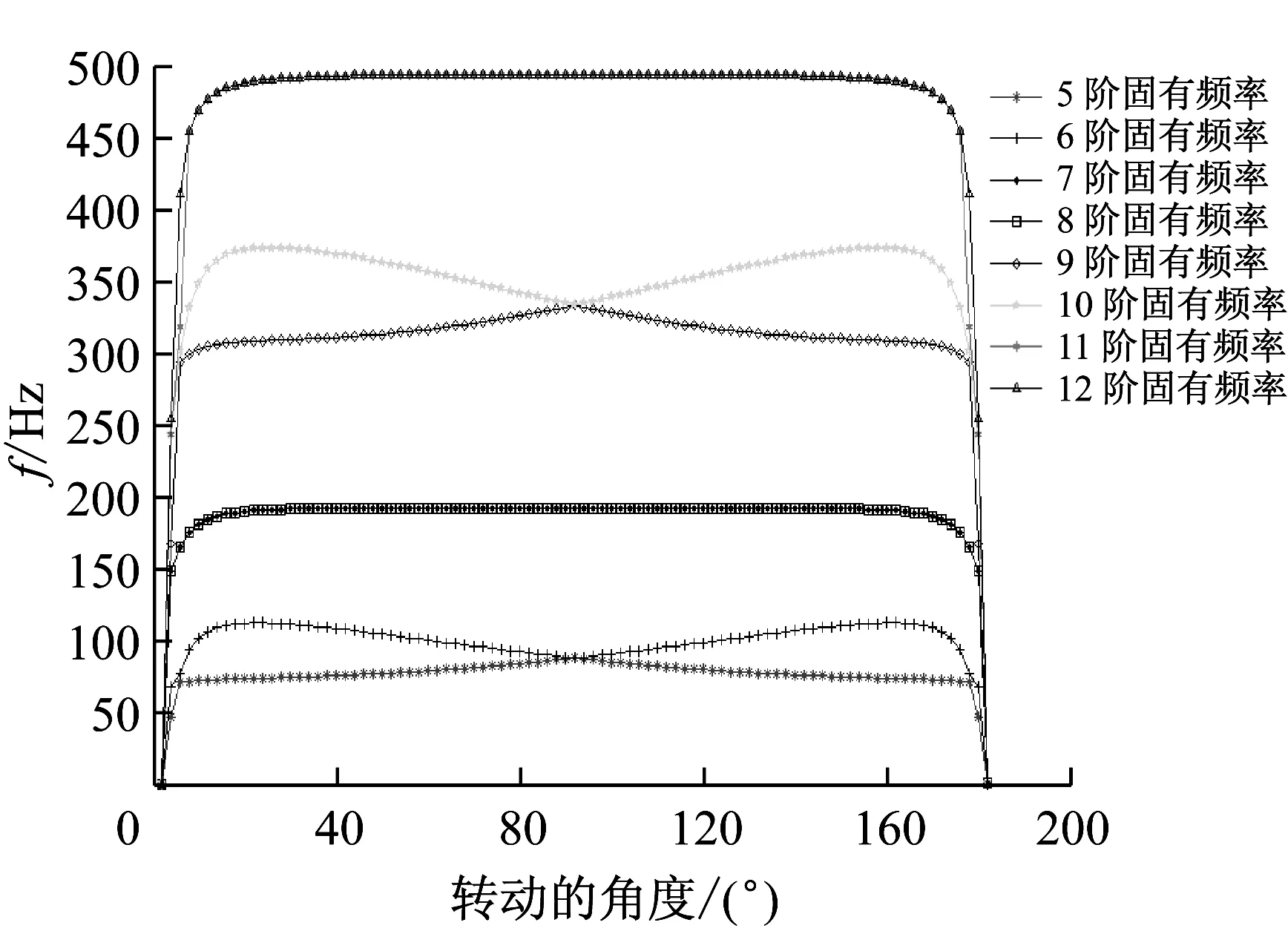
图3 5～12阶固有频率与展开角度关系

从图3可以看出，当平面阵列可展结构展开角度发生变化时，它的固有频率也会发生一定的改变，特别是在α=0°和α=180°这两个极限位置附近，固有频率突变并全部接近于0，说明这两个位置结构不稳定，所以工作时应该避免这两个位置，取频率相对稳定的展角α=20°～160°。

3.2 动态响应

平面阵列可展结构工作状态时约束和受力如图4所示，此时展开角度α=45°，节点a处所受外载如图5所示，分析其振动情况。

因加工方式的不同和微量元素的种类及含量的不同，铝合金的阻尼系数有很大的不同，航天中常用的铝合金的阻尼比可以分为三类：当近乎为纯铝时，此时阻尼很小可忽略不计，按无阻尼情况考虑，节点a处的响应如图6所示，由于惯性的作用，结构会在平衡位置附近进行振动，且最大振幅为8.7×10-5m，在0.4 s卸掉外载后节点即以此时的偏移量为最大振幅围绕新的平衡位置做周期振动，卸载前后周期一致；第二类是小阻尼铝合金，通过查阅文献[18]可知，某种铝合金的阻尼比为0.056 5，此时响应如图7所示，可以发现由外载导致的振动衰减很快，并且最大振幅减小为6.8×10-5m，仅为无阻尼时的78.2%；通过适当的阻尼增强处理，可将铝合金的阻尼比增大到1.02，此时响应如图8所示，可展结构将不再振动直接趋于平衡位置，且达到稳定的时间仅为前者的21%，故可以通过增大阻尼来减小外载带给可展结构的振动影响。

图4 可展结构工作状态Fig.4 Deployablestructureworkingstate图5 随时间变化的外载Fig.5 Loadovertime图6 无阻尼时点a横向振动的位置响应曲线Fig.6 Non-dampingpointalateraloscillationposi-tionresponsecurve图7 小阻尼时点a横向振动的位置响应曲线Fig.7 Smalldampingpointalateraloscillationposi-tionresponsecurve

图8 过阻尼时点a横向振动的位置响应曲线

4 结 论

(1)本文基于有限元法提出了一种对剪式单元机构动力学分析的规范化方法。首先分析得到剪式单元的叠加节点自由度与内部节点自由度，然后将其分开并以此为规范化后的位移列阵，再通过滤波法求出此时的规范矩阵，用其对剪式单元特性矩阵进行了规范化，将规范化后的特性矩阵直接循环首尾相加组装成平面阵列可展结构的刚度矩阵和质量矩阵，从而大幅度地降低了组装难度，提高了建模效率，同时也为编程提供了便利。

(2)利用程序编程计算平面阵列可展结构的固有频率并与ANSYS仿真结果进行比较，发现本方法计算值和仿真值最大误差不超过0.04%，可以说明规范化方法的正确性。同时，利用程序计算了可展结构展开角度α=0°～180°的5～12阶固有频率，结果表明α=20°～160°时固有频率是相对稳定的，机构应该在此区间内运动。

(3)针对平面阵列可展结构，进行了阻尼比为0(无阻尼)、0.056 5(小阻尼)和1.02(过阻尼)情况下的动态响应分析。当有阻尼时，外载变化引起的振动衰减很快，其中小阻尼时最大振幅仅为无阻尼时的78.2%，过阻尼时将不再发生振动，且到达稳定的时间仅为小阻尼时的21%，故可通过适当的增大阻尼来有效地减小结构振动。

参 考 文 献

[1] LANGBECKER T J. Kinematic analysis of deployable scissor structures[J]. International Journal of Space Structures,1999,14(1):1-15.

[2] CHERNIAVSKY A G, GULYAYEV V I, GAIDAICHUK V V, et al. Large deployable space antennas based on usage of polygonal pantograph[J]. Journal of Aerospace Engineering, 2005, 18(3):139-145.

[3] TAGAWA H, SUGIURA N, KODAMA S. Structural analysis of deployable structure with scissor-like-element in architectural design class[C]∥ IABSE Symposium Report. Nara: IABSE, 2015.

[4] 陈向阳, 关富玲, 陈务军,等. 复杂剪式铰结构的几何分析和设计[J]. 空间结构, 1998,4(1):45-51.

CHEN Xiangyang, GUAN Fuling, CHEN Wujun, et al. Geometry design and analysis of complex pantograph structures[J]. Spatial Structures, 1998,4(1): 45-51.

[5] 宋依洁, 熊海贝, 卿紫菲,等. 一种新型可展结构的探索[J]. 结构工程师, 2015, 31(5):48-53.

SONG Yijie, XIONG Haibei, QING Zifei, et al. Design and application of a new deployable structure[J]. Structural Engineers, 2015, 31(5): 48-53.

[6] 李庆营. 剪式铰可展结构力学性能分析[D]. 南京:东南大学, 2012.

[7] 陈耀. 新型对称可展结构的形态及展开过程分析与应用研究[D]. 南京:东南大学, 2014.

[8] ZHAO J, FENG Z, CHU F, et al. Chapter 11-mechanism theory and application of deployable structures based on scissor-like elements[J]. Advanced Theory of Constraint & Motion Analysis for Robot Mechanisms,2014:349-366.

[9] SUN Y, WANG S, MILLS J K. Kinematics and dynamics of deployable structures with scissor-like-elements based on screw theory[J]. Chinese Journal of Mechanical Engineering, 2014, 27(4):655-662.

[10] 纪斌, 王怀磊, 金栋平. 非对称平面剪铰结构展开过程分析与仿真[J]. 工程力学, 2013,30(7):7-13.

JI Bin, WANG Huailei, JIN Dongping. Analysis and simulation of the deployment process for asymmetric planar scissor structures[J]. Engineering Mechanics, 2013,30(7):7-13.

[11] 孙宏图, 袁茹, 王三民. 正方形可展机构的运动学与动力学特性研究[J]. 西北工业大学学报, 2013,31(4):620-623.

SUN Hongtu, YUAN Ru, WANG Sanmin. Kinematics and dynamics characteristics of square developable structure[J]. Journal of Northwestern Polytechnical University, 2013,31(4):620-623.

[12] SHAN W. Computer analysis of foldable structures[J]. Computers & Structures, 1992, 42(6):903-912.

[13] 杨毅, 丁希仑. 剪式单元可展机构静力学分析与拓扑优化设计[J]. 中国机械工程, 2010,21(2):184-189.

YANG Yi, DING Xilun. Analysis and topology optimization of deployable mechanism based on pantograph[J]. China Mechanical Engineering, 2010, 21(2):184-189.

[14] 刘国林, 王三民, 尚鹏. 剪式机构阵列可展结构的静力学分析方法与应用研究[J]. 中国机械工程, 2014,25(4):461-466.

LIU Guolin, WANG Sanmin, SHANG Peng. Static analysis method and application research of line array deployable structures based on SLE[J]. China Mechanical Engineering, 2014, 25(4):461-466.

[15] 戴云景, 方有亮. 可展索-桁架结构的有限元分析[J]. 科学技术与工程, 2007, 7(4):538-541.

DAI Yunjing, FANG Youliang. Finite element analysis of deployable cable-truss structures[J]. Science Technology & Engineering, 2007,7(4):538-541.

[16] 刘树青, 王兴松, 朱正龙. 一种剪式可展结构设计与动力学分析[J]. 机械设计, 2011, 28(10):55-60.

LIU Shuqing, WANG Xingsong, ZHU Zhenglong. Design and dynamic analysis of a scissor deployable structure[J]. Journal of Machine Design, 2011, 28(10):55-60.

[17] 曾攀. 有限元分析及应用[M]. 北京:清华大学出版社, 2004.

[18] 王莉.几种铝合金的力学性能及阻尼特性[J].轻合金加工技术,2005,33(12):48-50.

WANG Li. Influence of aging on mechanical properties and damping behavior of several aluminium alloy[J]. Light Alloy Fabrication Technology,2005,33(12):48-50.