在错误中反思成长

丁海科

对于统计与概率知识的考查，中考试题主要是通过分析和解读生活中的实例，让我们认识数学与生活的关系.这部分知识在中考中属于必考题，同时又是中档难度的试题.许多同学在复习和做题时重视不足，从而犯错失分.本文旨在帮助同学们对这部分知识进行纠错反思.希望大家读完本文，可以做到知其然，知其所以然.

一、概念不清慌中错

例1（2017·河南）八年级某同学6次数学小测验的成绩分别为：95分，85分，80分，100分，95分，95分，则该同学这6次成绩的众数和中位数分别是（ ）.

A.95分，95分 B.95分，90分

C.90分，95分 D.95分，85分

【错解】B.

【剖析】本题考查的是中位数与众数的概念.对于众数就是出现次数最多的数，没有悬念.问题在于中位数，首先要排序，这也是解决此问题的关键.从大到小或者从小到大排序，然后才可以去寻找中间位置，所以忘记排序是丢分的最主要的原因.

【正解】A.

二、审题不细犯错误

例2（2017·浙江）一个布袋里装有4个只有颜色不同的球，其中3个红球，1个白球.从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，则两次摸到的球都是红球的概率是（ ）.

【错解】B或C.

【剖析】本题考查概率问题，同学们会选择列表格或画出树状图来解决问题.红球与白球数量不等，所以从颜色来说，红色球与白色球被摸到的概率是不相等的.所以本题出错在于：其一，不区分红球1、红球2、红球3；其二，对于放回和不放回，有本质区别.因为审题不细致，从而导致失误丢分.这一点，尤其要引起大家的注意.

【正解】树状图：

摸两次球出现的可能结果共有16种，其中两次都是红球的可能结果共有9种，

所以P（两次都摸到红球选D.

三、图表不联必出错

例4某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查，并绘制成如图1、图2的统计图.已知“查资料”的人数是40人.

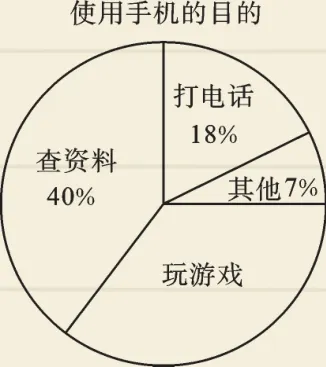
图1

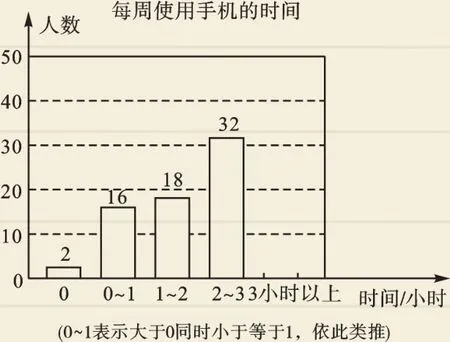
图2

请你根据以上信息解答以下问题：

（1）在扇形统计图中，“玩游戏”对应的圆心角度数是________；

（2）补全条形统计图；

（3）该校共有学生1200人，估计每周使用手机时间在2小时以上（不含2小时）的人数.

【错解】（1）90°；（2）22人；（3）384人.

【剖析】圆心角度数求错的根源有二，一是少部分同学忘记如何求度数；二是圆心角计算出错，导致错解.在补全条形统计图时，扇形图与条形图未进行综合解读，导致无法计算出使用手机“3小时以上”人数.最后一问，用部分估计整体，计算时少算部分人数导致错误.因此，图表类问题，必须综合地分析题目中给出的图与表，综合地分析数据，这样才不会再犯错.

【正解】（1）126°；（2）32人；（3）768人.

四、知识不融导致错

例5（2017·湖南）从-2，1，3这三个数中任取两个不同的数，作为点的坐标.

（1）写出该点所有可能的坐标；

（2）求该点在第一象限的概率.

【错解】（1）写出点的坐标不全；（2）由于第（1）问不对，导致第（2）问错误.

【剖析】本来三个数选出两个，不是难题，可是坐标要求数对必备有序性，就把问题变得复杂了.本题把概率问题和坐标系有机融合，富有新意又不失概率之美.面对“新”题，同学们显得无计可施了.我们回到问题的源头，点的坐标就是横坐标与纵坐标，先考虑横坐标可以取-2，1，3，再考虑纵坐标可以怎样取-2，1，3，所以共有6种结果，这样问题就轻松解决了.

【正解】（1）见列表；（2）

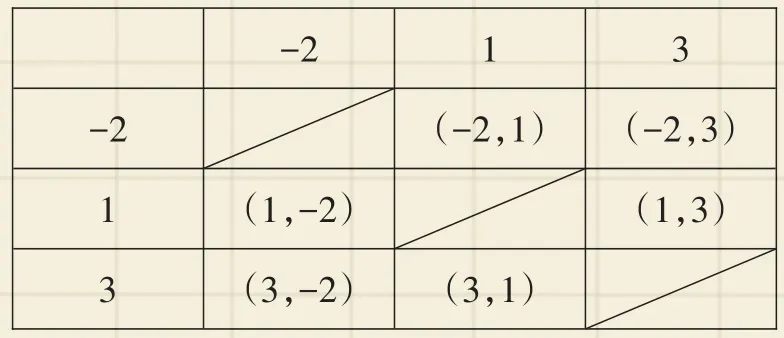
列表如图：

小试牛刀

自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费.具体收费标准如下：____________

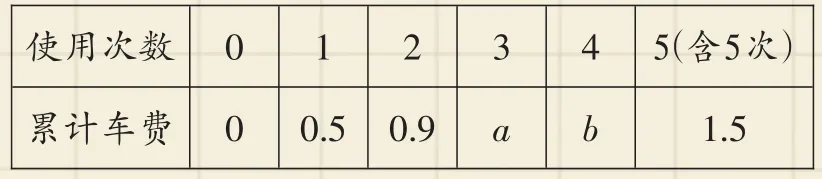
5（含5次）1.5使用次数__累计车费__0___0__1___2___0.5__0.9__3___a___4 b

同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：

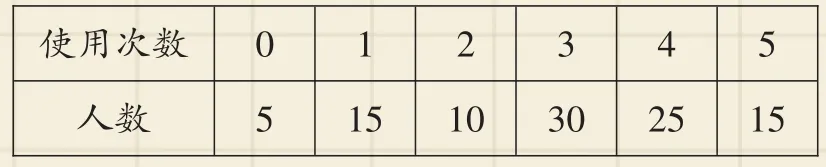
15_使用次数人数_____0____5___1____2____3____4____5_15___10___30___25

（Ⅰ）写出a，b的值；

（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元.试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利？说明理由.