中考题中的统计与概率

沈良琴

统计与概率知识在中考的选择、填空、解答题中都会经常出现.结合条形统计图、扇形统计图和折线统计图，利用平均数、众数、中位数、方差等对数据进行分析，从而得出相应的结论；利用树状图或列表的方法计算一些简单事件发生的概率常以解答题形式出现.一般统计与概率在中考试题中占总分值的12%～15%.下面通过一些实例加以说明：

一、数据的收集、整理、分析

例1（2017·怀化）下列说法中，正确的是（ ）.

A.要了解某大洋的海水污染情况，宜采用全面调查方式；

B.如果有一组数据为5，3，6，4，2，那么它的中位数是6；

C.为了解怀化市6月15日到19日的气温变化情况，应制作折线统计图；

D.“打开电视，正在播放怀化新闻节目”是必然事件.

【分析】本题考查了数据的收集与整理、数据的分析.解题关键是掌握全面调查和抽查的不同情况，掌握中位数的确定方法，知道什么情况下使用折线统计图以及必然事件的概念.

【解答】选项A中某大洋中的海水面积非常广阔，并且量特别大，因此不能采用全面调查，而应该抽样调查；选项B中将这组数据从小到大排列为2，3，4，5，6，所以中位数是4；选项C中要反映温度变化情况，最合适的统计图是折线统计图；选项D中随机打开电视可能是怀化新闻节目，也可能是其他节目，所以“打开电视，正在播放怀化新闻节目”不是必然事件.故选C.

【点评】本题易错点是在找中位数的时候，没有把所有数据按照一定顺序排列，就去找位于中间的数.

【变式练习1】（2017·乌鲁木齐）下列说法中，正确的是（ ）.

A.“经过有交通信号灯的路口，遇到红灯”是必然事件

B.已知某篮球运动员投篮投中的概率是0.6，则他投10次一定可投中6次

C.处于中间位置的数一定是中位数

D.方差越大数据的波动越大，方差越小数据的波动越小

【答案】D.

二、三数两差

例2（2017·枣庄）下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：________________________

180 8.1_________________甲乙_____丙_____丁__平均数（mm）__方差_______185___3.6____180____3.6____185 7.4

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）.

A.甲 B.乙 C.丙 D.丁

【分析】首先比较平均数，平均数相同时选择方差较小的运动员参加.

【解答】∵甲、丙的平均数大于乙、丁的平均数，又∵甲的方差小于丙的方差，∴甲的成绩更稳定，应选择甲参赛.故选A.

【点评】此题考查了平均数和方差，正确理解方差与平均数的意义是解题关键.

【变式练习2】（2017·青岛）小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法中错误的是（ ）.

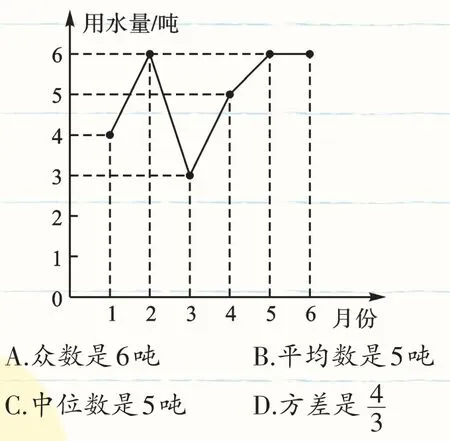
【答案】C.

三、统计图表

例3（2017·大连）某校为了了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.________________________________

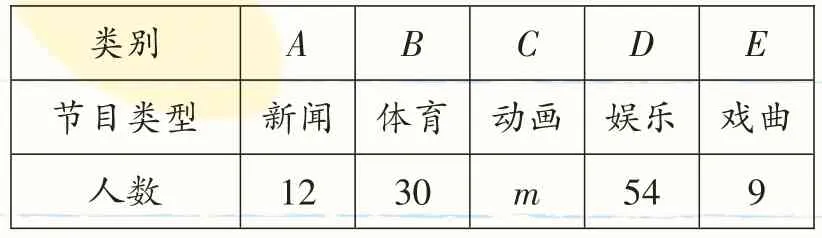
____类别__节目类型____人数A____B____C____D____E__新闻__12体育__30动画_m娱乐__54____戏曲9__

根据以上信息解答下列问题：

（1）被调查的学生中，最喜爱体育节目的有_______人，这些学生数占被调查总人数的百分比为_______%；

（2）被调查学生的总数为_______人，统计表中m的值为________，统计图中n的值为_______；

（3）在统计图中，E类所对应扇形圆心角的度数为_______°；

（4）该校共有2000名学生，根据调查结果，估计该校最喜爱新闻节目的学生数.

【分析】（1）直接通过表格读取最喜爱体育节目的人数，通过扇形统计图读取喜爱体育的人数占被调查总人数的百分比；（2）通过喜爱体育的人数和占被调查总人数的百分比求出被调查学生的总数，用总数减去A、B、D、E项目的人数求出m值，用D项目的人数除以被调查学生的总数即可得到n的值；（3）求出E类学生数占被调查总人数的百分比，用这个百分比乘360°即可；（4）求出喜爱新闻节目的人数占被调查总人数的百分比，进而乘该校总人数求得结果.

【解答】（1）30，20；（2）150，45，36；（3）21.6；（4）解：，答：估计该校最喜爱新闻节目的学生数是160人.

【点评】本题考查了统计表和扇形统计图，解题的关键是综合运用统计表和统计图给出的信息求出被抽查的总人数.

【变式练习3】（2017·泰州）“泰微课”是学生自主学习的平台.某初级中学共有1200名学生，每人每周学习的数学泰微课都在6至30个之间（含6和30）.为进一步了解该校学生每周学习数学泰微课的情况，从三个年级随机抽取了部分学生的相关学习数据，并整理、绘制成统计图如下：

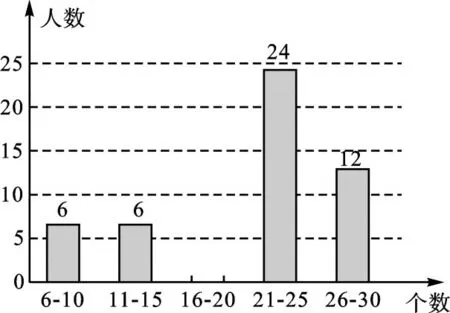
每周学习数学泰微课人数的条形统计图

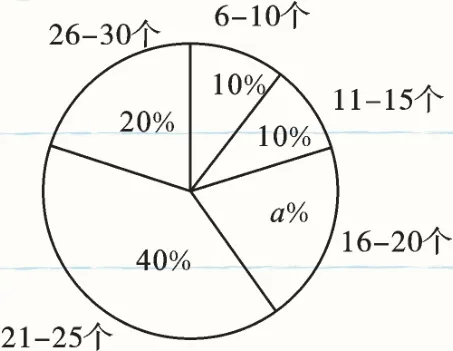
每周学习数学泰微课人数的扇形统计图

根据以上信息完成下列问题：

（1）补全条形统计图；

（2）估计该校全体学生中每周学习数学泰微课在16至30个之间（含16和30）的人数.

【答案】（1）a%=1-10%-10%-20%-40%=20%，6÷10%×20%=12（人）.

补全条形统计图如下：

每周学习数学泰微课人数的条形统计图

（2）解：1200×（20%+40%+20%）=960（人）.

答：该校全体学生中每周学习数学泰微课在16至30个之间的约有960人.

四、概率

例4（2017·连云港）为落实“垃圾分类”，环卫部门要求垃圾要按A，B，C三类分别装袋，投放，其中A类指废电池，过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料，废纸等可回收垃圾.甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类.

（1）直接写出甲投放的垃圾恰好是A类的概率；

（2）求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.

【分析】（1）所有等可能的结果有三个，即：A类、B类、C类，A类只有一种，根据概率公式即可求出概率；（2）列出树状图，先求出所有等可能的结果，再找出符合条件的可能数，然后根据概率公式求出概率.

【解析】（1）甲投放的垃圾恰好是A类的概率是

（2）列出树状图如图所示：

由图可知，共有18种等可能结果，其中乙投放的垃圾恰有一袋与甲投放的垃圾是同类的结果有12种.

所以，P（乙投放的垃圾恰有一袋与甲投放的垃圾是同类）

即乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率是

【点评】一步试验概率直接根据计算；两步试验概率可以用树状图来解答，也可以用列表法来解答；三步或三步以上试验概率只能用树状图来解答.另外要注意是放回事件还是不放回事件，列表法或画树状图法可以不重复不遗漏地列出所有可能的结果.

【变式练习4】（2017·南京）全面两孩政策实施后，甲、乙两个家庭有了各自的规划.假定生男生女的概率相同，回答下列问题：

（1）甲家庭已有一个男孩，准备再生一个孩子，则这个孩子是女孩的概率是_______；

（2）乙家庭没有孩子，准备生两个孩子，求至少一个女孩的概率.

【答案】（1）.（2）乙家庭没有孩子，准备生两个孩子，所有可能出现的结果有：（男，男）、（男，女）、（女，男）、（女，女），共有4种，它们出现的可能性相同.所有的结果中，满足“至少有一个孩子是女孩”（记为事件A）的结果有3种，∴