例谈函数问题踩点得分技巧

赵莹银

对于同一道题，有些人理解得透彻，有些人理解得浅显，有些人解决的途径多，有些人解决的途径少.为了区分这一情况，中考阅卷时，我们往往采用人性化给分原则，也就是说在这道题考查的知识点中，你答出了几点，我们就给多少分.我们称这种方法为“分步踩点给分”，对学生而言就是“分步踩点得分”.

具体怎么操作呢？在这里，笔者将之细化为两小部分，一部分针对“会而不对，对而不全”的老大难问题，另一部分则是针对没把握全解出来的问题.

中考阅卷时，我们常常替一些考生感到惋惜.这部分同学往往题目会做，但是答案是错的，或者答案是对的，但是解答过程会由于逻辑思维缺陷、概念错误或者缺少关键步骤而失分.对于这种现象，我们要在平时的做题中注意表达的正确，考虑的周密，书写的规范，语言的科学.

例题（2017·南通）已知直线y=kx+b与抛物线y=ax2（a＞0）相交于A，B两点（点A在点B的左侧），与y轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D.

（1）若∠AOB=60°，AB∥x轴，AB=2，求a的值；

（2）若∠AOB=90°，点A的横坐标为-4，AC=4BC，求点B的坐标；

（3）延长AD，BO相交于点E，求证：DE=CO.

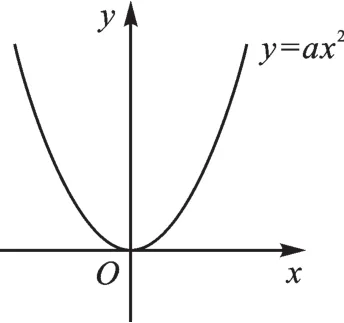
图1

【阅卷评分标准】（1）如图2，∵AB∥x轴，∴点A，B关于y轴对称.

∵AB=2，∴AC=BC=1.

∵∠AOB=60°，∴OC=3AC=3.

又∵点A在第二象限，∴点A的坐标是

∴解得

图2

（2）如图3，过点B作BF⊥x轴，垂足为F，则AD∥CO∥BF.

∵点A的横坐标为-4，∴DO=4，AD=16a，

∴OF=1，∴点B的横坐标为1，

∴BF=a.（5分）

∴点B的坐标是

图3

（3）法一：如图4，连接DC，过点B作BF⊥x轴，垂足为F，

图4

∵AD∥CO，

∴四边形DEOC是平行四边形.

∴DE=CO.（13分）

法二：设A（x1，ax12），B（x2，ax22），直线OB的解析式为y=mx，易得m=ax2，

∴直线OB的解析式为y=ax2x.

∵AE∥y轴，∴xE=xA=x1，∴yE=ax1x2.（10分）

∵直线y=kx+b与抛物线y=ax2（a＞0）相交于A，B两点，

∴x1，x2是方程ax2-kx-b=0 的两根，则x1·

在y=kx+b中，由xC=0，得yC=b，∴OC=b.

∴DE=CO.（13分）

【踩点得分提示】从上面评分标准可以看出，第（1）小题3分，第（2）小题5分，第（3）小题5分，而第（1）小题的3分又分成两部分，求出点A的坐标得2分，求出a的值得1分.第（2）小题的5分同样被分成3个部分，求出BF的值得2分，证得AD·BF=OF·OD得2分，求出点B的坐标得1分.

所以同学们，在解答此类问题时，首先要写全必要的解答过程.如果只有结果，没有解答过程，那么你有可能只能得结果分，比如第（2）小问，如果你只写出B点坐标，那么你只能得1分.

其次对大部分同学来说，对于没把握全解出来的问题怎么办呢？这是大家关心的问题.这类问题的解答技巧又是什么呢？笔者认为，最好的办法就是“以退为进”.你可以把题目从抽象退到具体、从未知退到已知，从一般退到特殊，从整体退到部分.退到你能解决的问题，把你知道的解题过程，无论多少，都写出来，想到多少写多少，让阅卷老师从中寻找给分点，踩点给分.