一类新四维混沌系统的动力学分析

王艳玲，雷腾飞，张艳萍，夏祥祥，沈 敏

(齐鲁理工学院电气信息工程学院，山东济南，250200)

混沌是广泛存在于大自然中的一种非线性现象，最显著的特征是对初值的敏感性。自Lorenz提出第一个混沌系统以来［1］，混沌系统构建工作一直在进行且取得了丰硕的科研成果。1999年，陈关荣教授等根据洛伦兹系统提出了Chen系统［2］，Chen系统与洛伦兹系统代数式相似，但拓扑不等价，属于对偶混沌系统;2002年，中国科学研究院研究员吕金虎等提出了Lü系统［3］，根据线性代数式分类，该系统为洛伦兹系统与Chen系统的桥梁系统;2004年，刘崇新教授等提出了Liu系统［4］;2005年，齐国元等人提出了具有三个交叉非线性项的Qi系统。最近几年，新的混沌系统不断涌现，但混沌特性较强的系统较少［5－11］。由于混沌理论广泛应用于图像加密［11］、通信保密、激光系统等方面，则构造混沌系统依然是系统应用中的重点与热点［5－14］。

随着混沌系统的构建工作的不断深入与研究，一类新的混沌系统提出即具有隐藏吸引子的混沌系统，该系统不是采用线性代数式分类方法，而是根据平衡点的相关特性进行分类。隐藏吸引子混沌系统的平衡点有以下几种情况:独立的无穷平衡点、无平衡点以及稳定的平衡点。文献［9］针对一类具有稳定平衡点的改进Jerk混沌系统，研究该混沌系统的动力学特性;文献［10］对具有隐藏吸引子(无平衡点)的混沌系统，进行了基本动力学行为的研究。

首先，根据已有文献利用反馈控制法得到一类新的4D混沌系统，同时，此采用相图、分岔图以及李指数等刻画方法研究了系统的混沌特性。为了深一步研究双参数变化下系统的混沌行为，文中采用双参数变化下的空间复杂度加以阐述，本系统的提出与分析为新混沌在视频以及图像等多媒体增加领域奠定了基础。

1 混沌系统模型

1.1 混沌系统

文章在文献［8］的基础上重新构建一类新的四维自治混沌系统即:

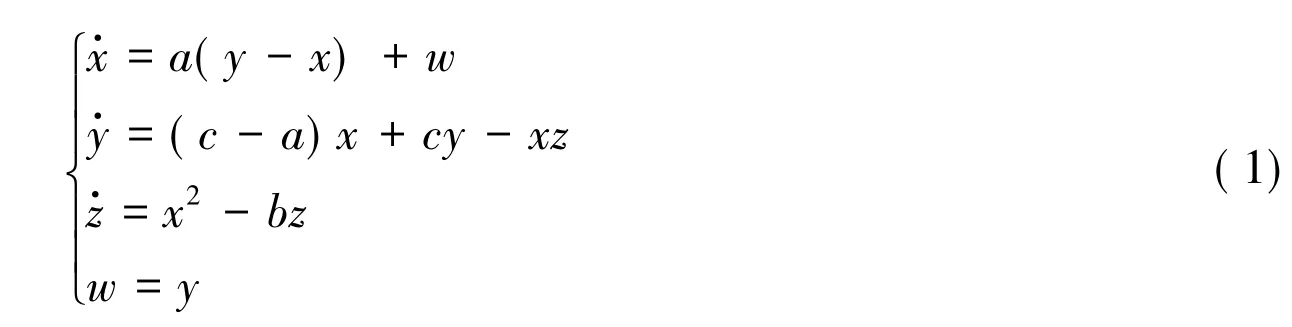
其中 x，y，z，w 为四个基本状态变量，a，b，c为系统(1) 参数，当a=38，c=30，b=3 时系统(1)存在混沌特性，混沌吸引子相图如图1所示。通过Matlab仿真计算，可得出系统(1)的四个 LE 为 LE1=2.763453，LE2=0.0，LE3=－0.0，LE4= －13.735161，如图 2 所示。根据维数定义，可计算出系统的维数为分数，即系统存在分形特性。

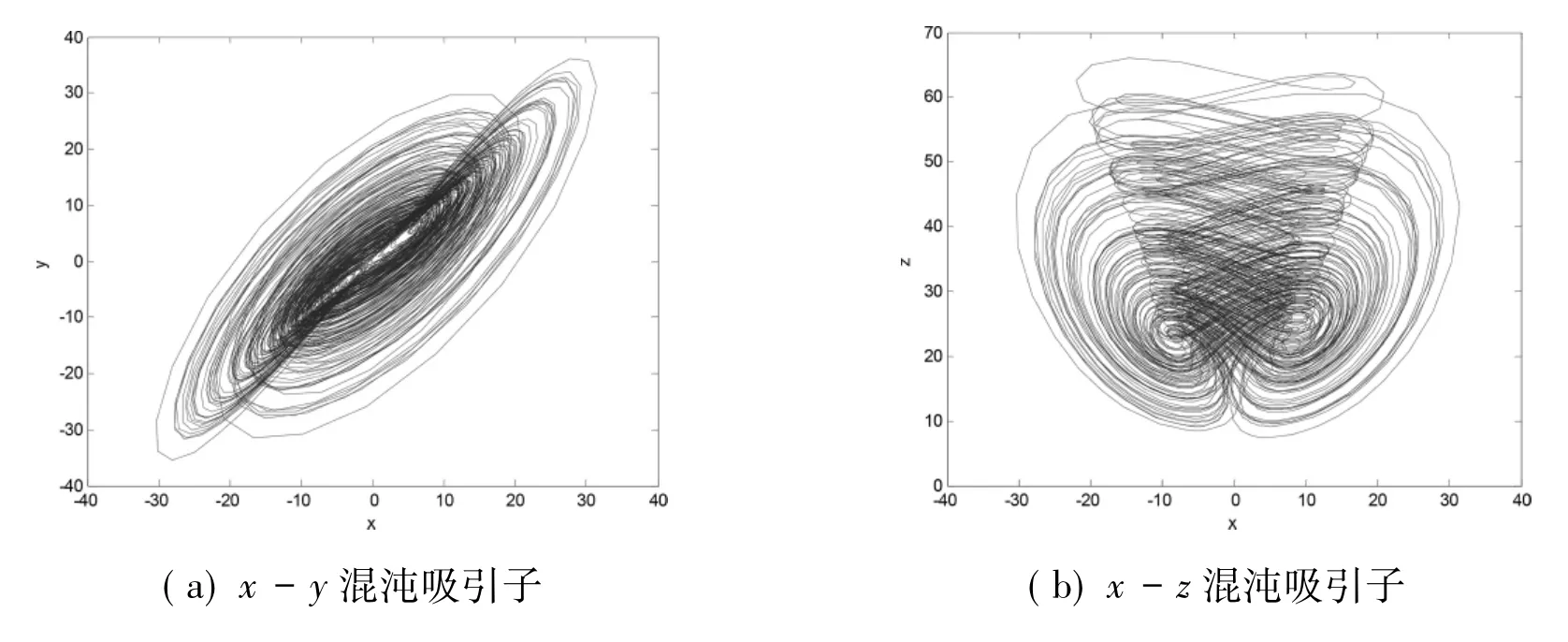
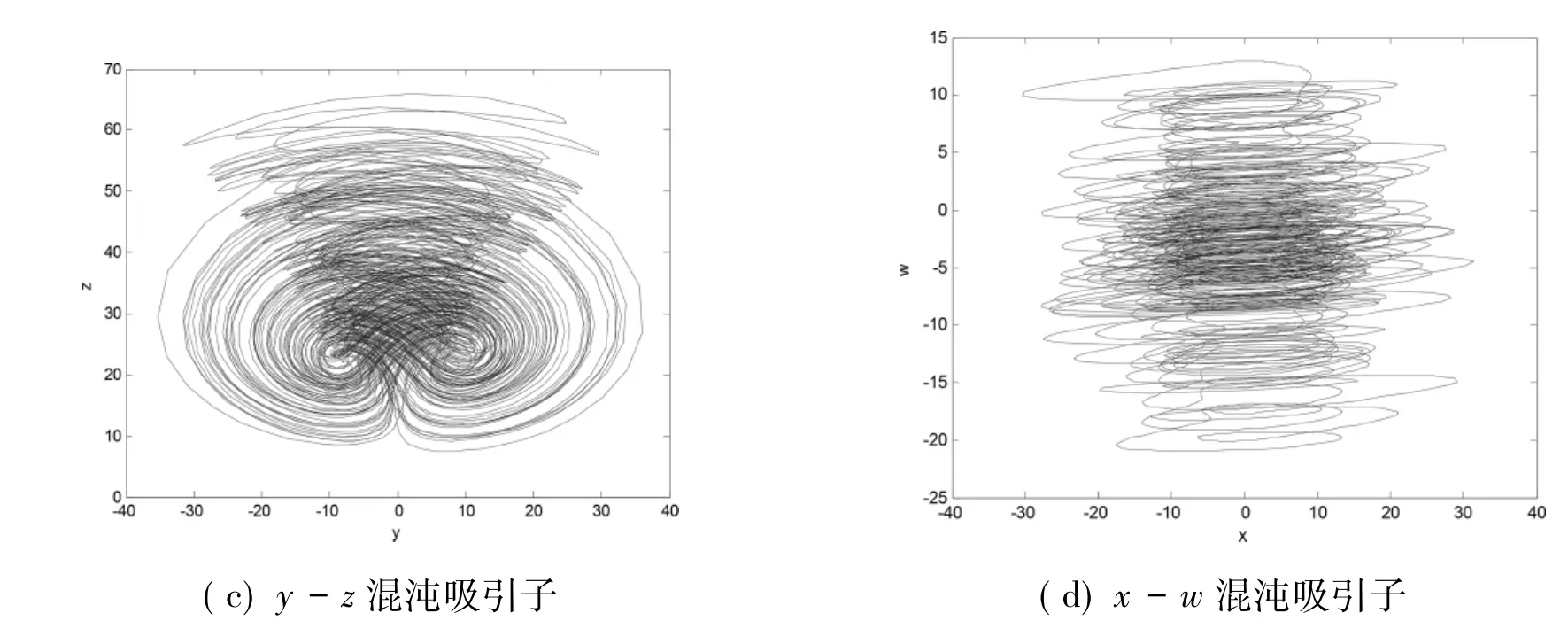
图1 系统(1)混沌吸引子Fig.1 Chaotic attractor of system(1)

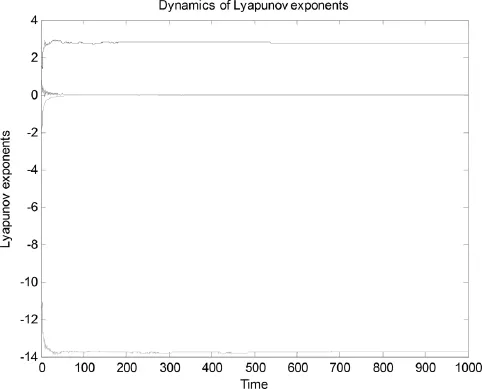
图2 固定参数下系统(1)LE谱Fig.2 LE spectrum of system(1)under fixed parameters

1.2 二进制测试分析

最近，刻画混沌系统另一种方法即二进制测法(0－1测试)，在较多文献中被介绍应用。二进制测试方法是在时间序列上进行的分析研究。二进制测试出的结果即某个序列下的p－s相图。p－s相图中的轨迹只是提供一个简单的视觉测试，并没有从定量的系统加以阐述。在p－s平面内若有界轨迹则为规则的状态即表现出收敛，即为非混沌态。若类似布朗运动无界轨迹且较为分形(发散)态则说明系统为混沌态。利用0－1测试对系统(1)的x，y，z，w四个序列运用Matlab进行仿真，得到的p－s相图如图3所示，可以看出系统(1)具有混沌特性。

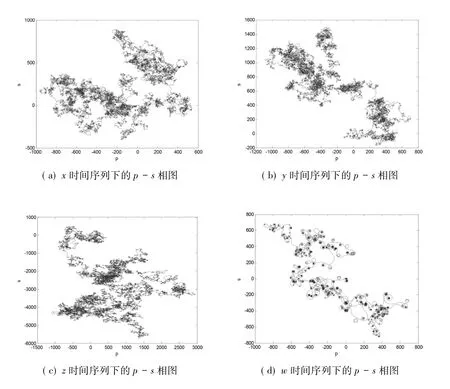
图3 混沌系统(1)的p－s图Fig.3 P－s plane diagram of chaoticsystem(1)

1.3 混沌系统平衡点分析

令系统四个方程为零，即可求出系统的平衡点E=(0，0，0，0)，在平衡点E=(0，0，0，0)对系统进行线性化，得Jacobian矩阵为:

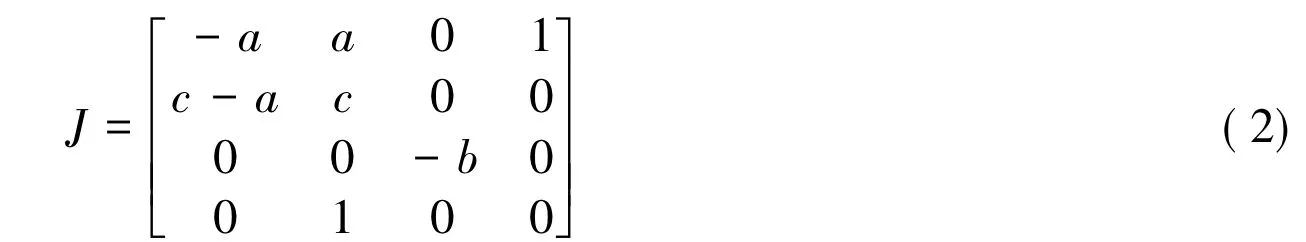
代入 a，b，c，求得Jacobian 矩阵特征值为 λ1=－ 33.1，λ2=25.183，λ3=0.00，λ4= － 3，根据劳斯判据λ2实部为正数，则点E0为不稳的点。

2 参数的影响

对于系统分析，其分析参数变化对系统影响尤为重要，对于混沌系统，通常采用分叉图以及LE谱研究其参数对系统影响。为此，文章对系统分岔图与Lyapunov指数变化规律进行了探索。

参数a=38，c=30，参数b变化，b∈［0，10］混沌系统(1)的分岔图与LE谱如图4所示。可以看出系统b∈［5.5，10］处于非混沌态即周期或拟周期态，a∈(0，5.5)处于混沌状态。混沌区域最大LE大于0，且复杂度较高，非混沌态系统最大LE等于0且复杂度较低，如图4(b)与图5所示。混沌相图如图6(a)所示，周期相图如图6(b)所示。

图4 b变化时系统(1)的关于x分岔图与Lyapunov指数谱Fig.4 X bifurcation diagram and lyapunov exponent spectrum of system(1)with the variation of b

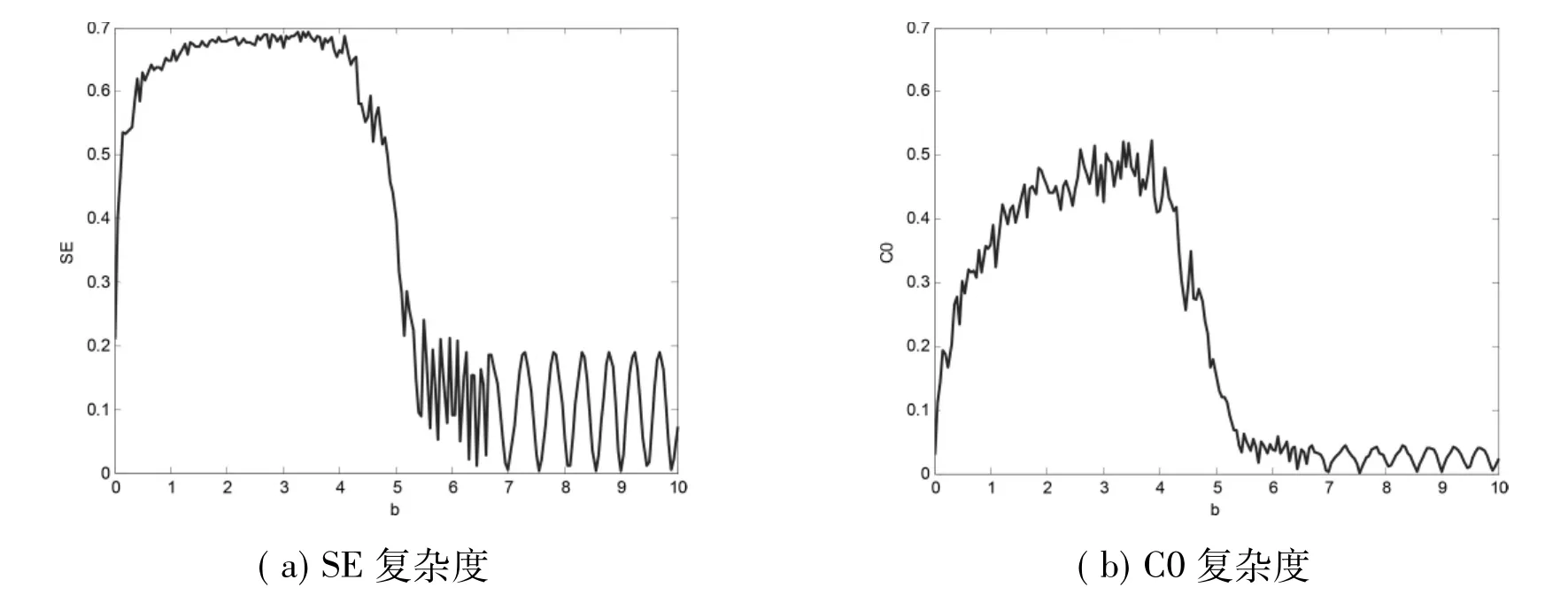
图5 b变化时系统(1)复杂度Fig.5 Complexity of system(1)with the variation of b

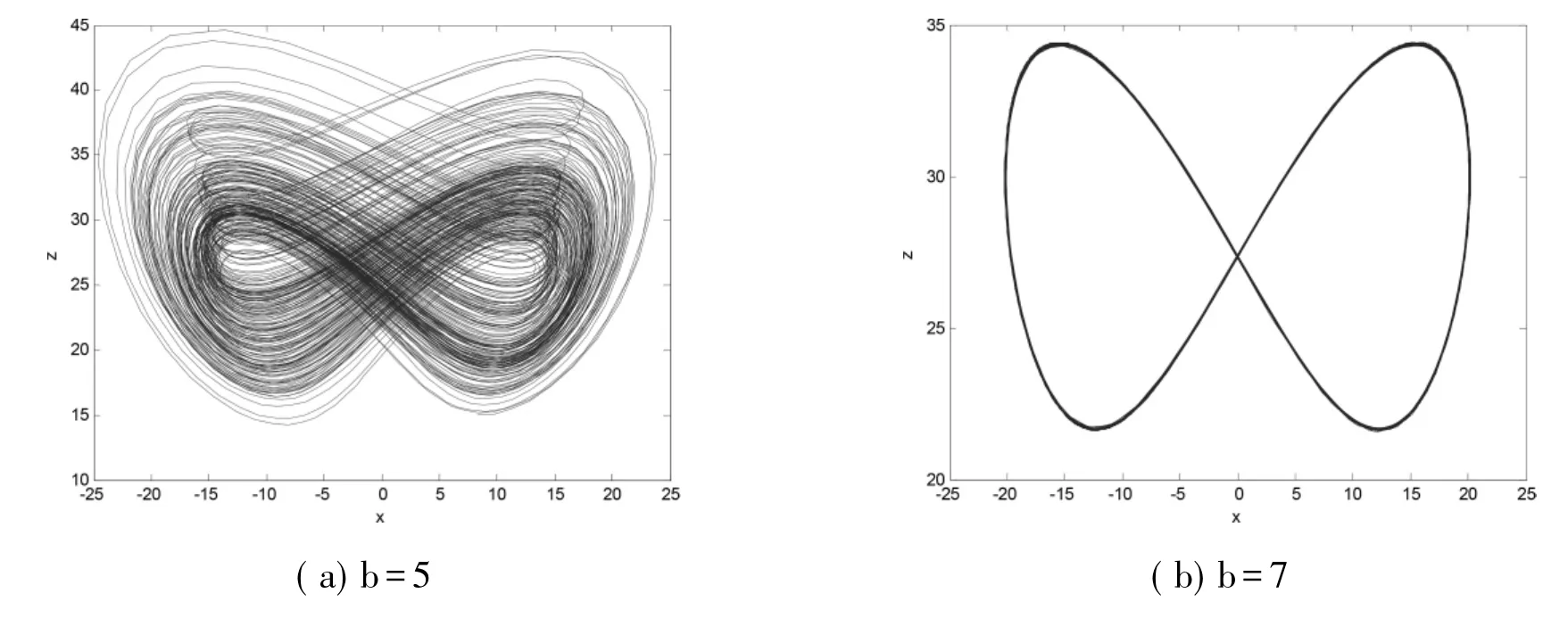
图6 b变化时系统(1)的相图Fig.6 Phase diagram of system(1)with the variation of b

同理，固定参数a=38，b=3，改变参数c，c∈［20，35］混沌系统(1)的分岔图与LE谱如图7所示，复杂度如图8所示。从分岔图中可看出c∈［20，21.5］∪［32.5，35］系统处于周期窗口，则可判定系统是通过倍周期分岔进入混沌状态的，此时对应的最大LE数等于0且复杂度较低，如图7(b)与图8所示。其他区域为混沌区域，系统的最大LE大于0且复杂度较高。为了验证进一步验证系统相关特性，文中给出了系统的相图，如图9所示。周期一如图9(a)所示，周期二如图9(b)所示。

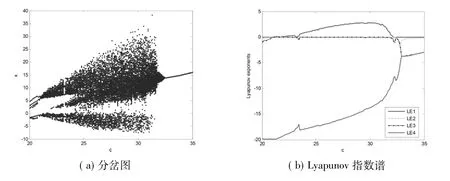
图7 c变化时系统(3)的关于x分岔图与Lyapunov指数谱Fig.7 X bifurcation diagram and Lyapunov exponent spectrum of system(1)with the variation of c

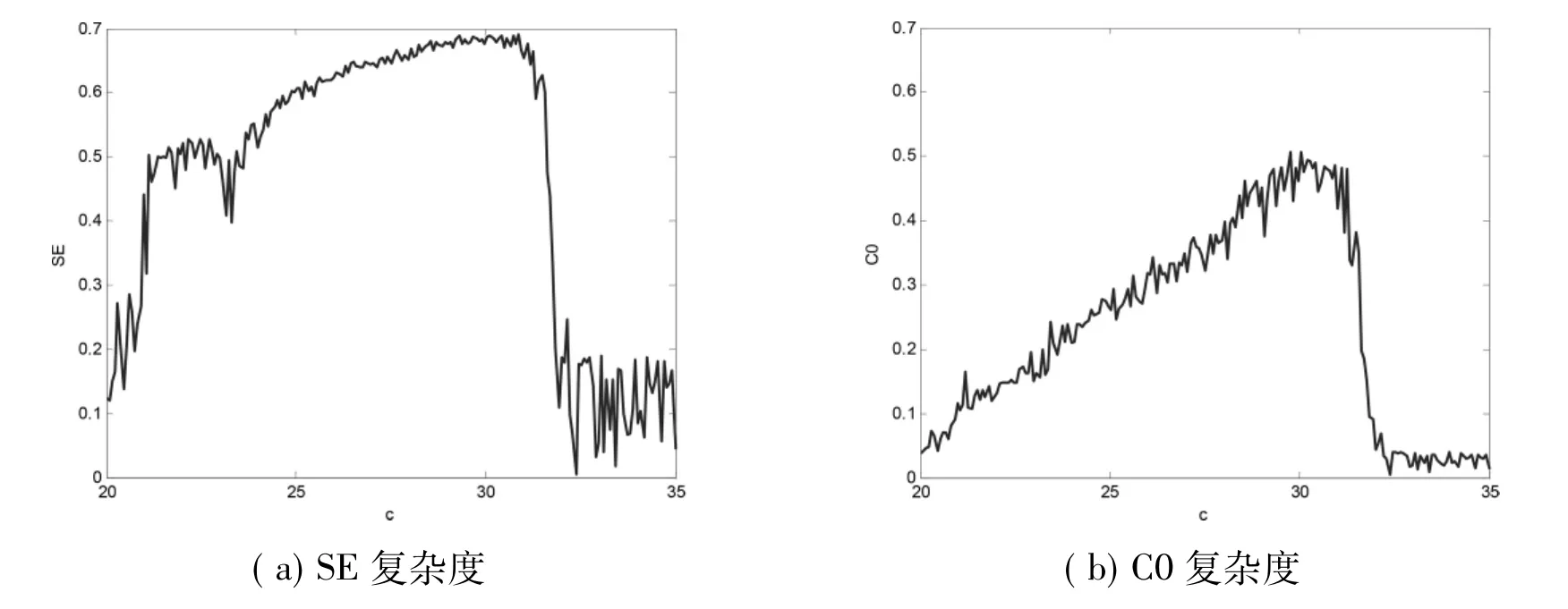
图8 c变化时系统(1)复杂度Fig.8 Complexity of system(1)with the variation of c

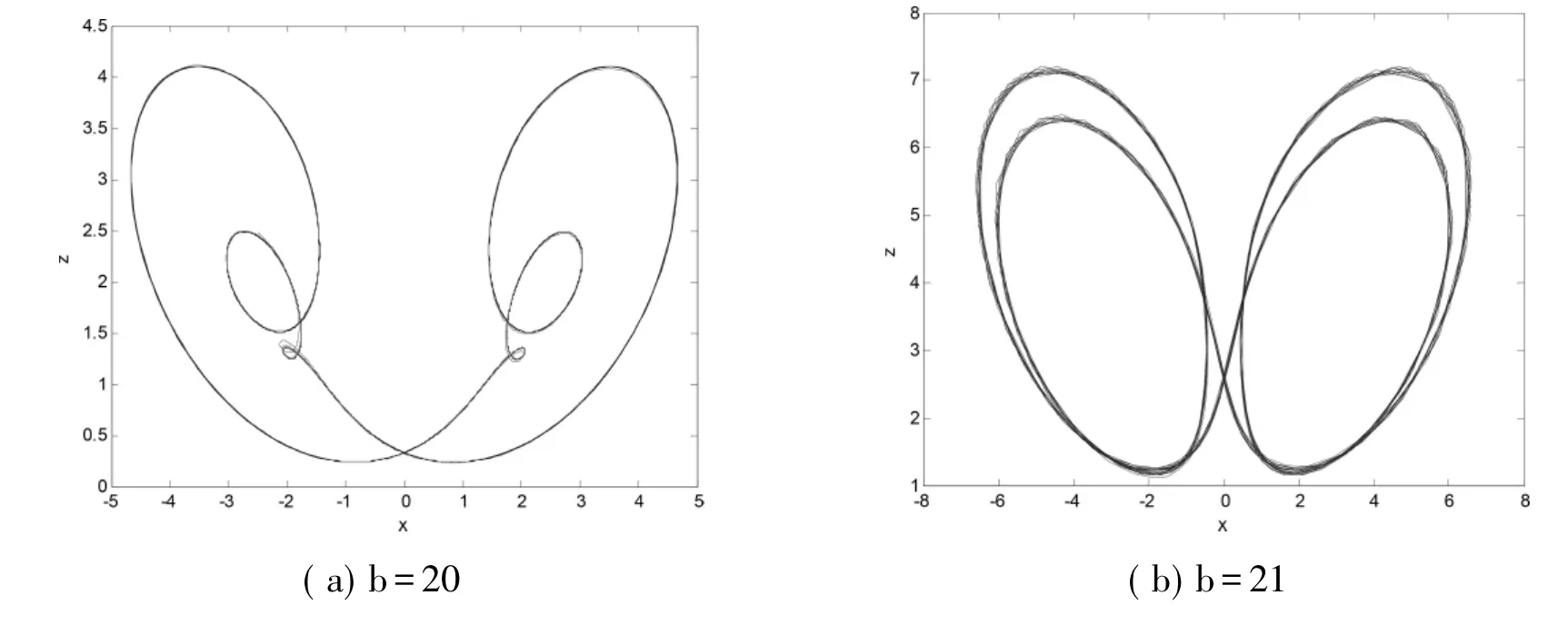
图9 c变化时系统(1)的相图Fig.9 Phase diagram of system(1)with the variation of c

为了研究两个参数同时变化下的混沌系统状态，文中采用分岔空间图即两个参数下复杂度(SE与C0复杂度)，双参数变化下的复杂度如图10所示。很容易观察出，图10与图5、图8具有一致性，且两个参数同时变化，参数c与参数b相互制约，参数c变化对系统影响较大。

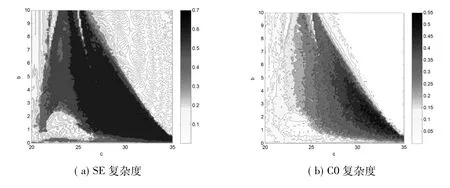
图10 双参数(b/c)变化下系统(1)的复杂度Fig.10 Complexity of system(1)with the variation of double parameters(b/c)

3 结论

文中根据已有文献，重新构造了一类新的混沌系统，且通过分岔图、LE数与二进制测试等多种分析刻画方法研究其四维系统的混沌特性行为。为了更为详细准确全面分析系统混沌特性，采用了双参数变化下复杂度(SE与C0)，说明其系统的混沌空间，因本系统结构代数较为简单，可广泛应用于混沌保密以及视频、图像加密等领域。

参考文献:

［1］LORENZ EN.Deterministic nonperiodic flow［J］.Journal of Atmospheric Science，2004，20(02):130－141.

［2］CHEN G，UETA T.Yet another chaotic attractor［J］.International Journal of Bifurcation ＆ Chaos，1999，9(07):1465－1466.

［3］LV J，CHEN G.A new chaotic attractor coined［J］.International Journal of Bifurcation and chaos，2002，12(03):659－661.

［4］LIU C，LIU T，LIU L.A new chaotic attractor［J］.Chaos Solitons ＆ Fractals，2004，22(05):1031－1038.

［5］LIU C，LIU L，LIU T，et al，A new butterfly－shaped attractor of Lorenz－like system［J］.Chaos Solitons ＆Fractals，2006，28(05):1196－1203.

［6］TIGAN G，OPRI爦 D.Analysis of a 3D Chaotic System［J］.Chaos Solitons ＆ Fractals，2006，36(05):1315－1319.

［7］周小勇.一种具有恒Lyapunov指数谱的混沌系统及电路仿真［J］.物理学报，2011，60(01):54－65.

［8］李春来，禹思敏，罗晓曙.一个新的混沌系统的构建与实现［J］.物理学报，2012，61(11):127－136.

［9］WANG Z，SUN W，WEI Z，et al.Dynamics and delayed feedback control for a 3D jerk system with hidden attractor［J］.Nonlinear Dynamics，2015，82(1－2):577－588.

［10］WEI Z.Dynamical behaviors of a chaotic system with no equilibria［J］.Physics Letters A，2011，376(02):102－108.

［11］彭再平，王春华，林愿，等.一种新型的四维多翼超混沌吸引子及其在图像加密中的研究［J］物理学报，2014，63(24):101－110.

［12］雷腾飞，刘彦芬，陈众起，等.一类具有吸引子共存新混沌系统的动力学分析、电路仿真及应用［J］.曲阜师范大学学报(自然科学版)2017，43(03):35－43.

［13］雷腾飞，付海燕，陈恒，等，一类新的纠缠混沌系统的动力学分析［J］，河北师范大学学报(自然科学版)，2017，41(03):213－221.

［14］杨敏，俞建宁，张建刚，等，一个混沌纠缠系统的动力学分析［J］，温州大学学报(自然科学版)，2014，35(03):12－17.