循环图能量的上界

周后卿

(邵阳学院 理学院，湖南邵阳，422000)

1978年，著名数学化学家I.Gutman［1］提出了简单图的能量的概念。化学家在研究共轭的碳氢化合物的性质时，发现总π电能与共轭的碳氢化合物形成时所释放的能量密切相关，π电能的计算最终归结为其分子图的所有特征值的绝对值之和［2－4］。图的谱理论与Huckel分子轨道理论之间存在明确的对应关系，如图的谱对应于分子能级，特征向量对应于分子轨道等等。

图的能量定义为图的所有特征值的绝对值之和，用符号E(G)表示，即 E(G)=图的能量是图的一个不变量，对图的能量研究已有许多文献［5－9］。

文中在已有文献的基础上，研究循环图的能量的上界。

1 有关能量上界的一些结论

设G=(V，E) 是一个简单图，顶点集 V(G)={v1，v2，…，vn}，边集 E(G)，令边数顶点vi的度用di表示，最大度、最小度分别用Δ，δ表示。设图G的邻接矩阵为A，A的特征值为λ1≥λ2≥…≥λn，称λ1为图G的谱半径。A的行列式记为|A|，A的特征值具有下列性质:

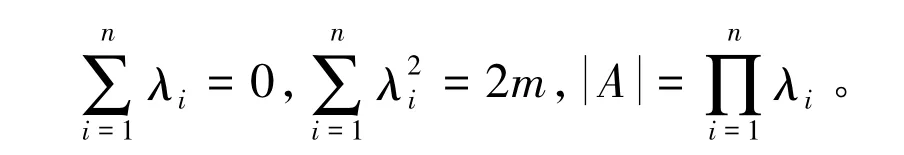
一个图是奇异的，如果它至少有一个特征值为0;对奇异图，显然有一个图是非奇异的，如果它的所有特征值都不为0，因而

关于图的上界，已有许多结论。

1971年，McClelland［10］发现了能量的一个上界:

Koolen and Moulton［11］证明了:G是一个具有n个顶点m条边的简单图，若2m≥n，则等式成立当且仅当G是完全图Kn或(n为偶数)。若2m ＜n，则E(G)≤2m，等式成立当且仅当G是边不相交的并或为孤立顶点。

这个上界优于McClelland给出的上界。

若G是一个二部图，文献［12］证明了下列结论:

图G=C(n，S)称为循环图，如果它的邻接矩阵是一个循环矩阵，它是循环群上的Cayley图。循环图具有很好的性质，它是点可迁的。某些网状互联网络实质上就是循环图对应的网络，对循环图的网络应用研究有很多文献［13－14］。在过去20多年里，循环图不断出现在编码理论，VLSI设计，Ramsey理论，并行计算和分布式计算中。

设n为正整数，给出集合{0，1，2，…，n－1}的一个子集S(又叫符号集)，设S={a1，a2，…，ak}，使得，则循环图C(n，S) 有i±a1，i±a2，…，i±ak(mod n) 个顶点与顶点i相邻。若则循环图C(n，S)是一个度为2k的正则图;若(n为偶数)，则循环图C(n，S)是一个度为2k－1的正则图。设循环图C(n，S)的邻接矩阵为

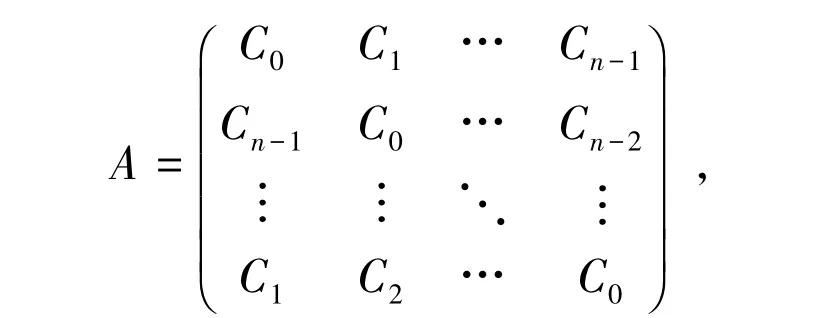
则A的特征值为［15］

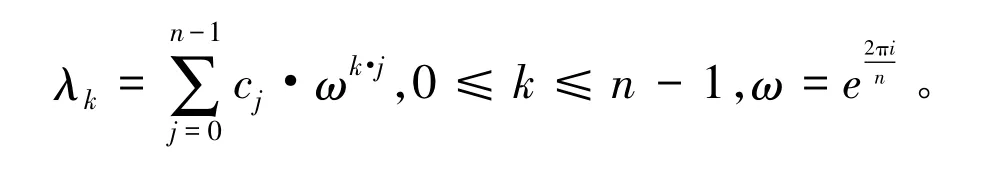
2 引理与定理

下面证明文中的主要结论。为了证明我们的结论，需要以下引理。

引理1［16］设G是具有n个顶点m条边的简单图，那么，G的特征值λi(1≤i≤n)满足

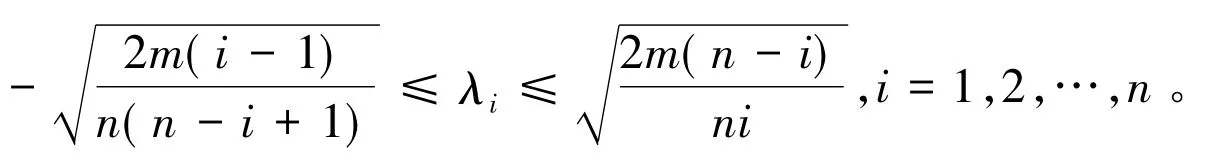
引理2［17］设G是一个具有n个顶点m条边，度序列为d1，d2，…，dn的简单图，则

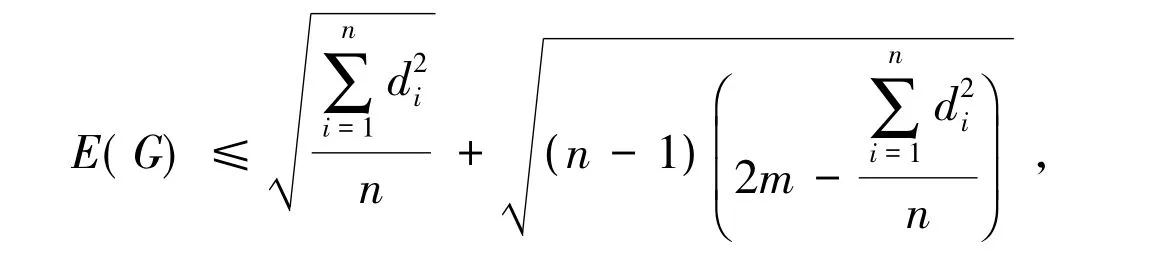
等式成立当且仅当G是完全二部图或(n为偶数)。

现在证明文中结论。

定理1 设G是一个具有n(n＞2)个顶点，度为r，行列式为的循环图，则

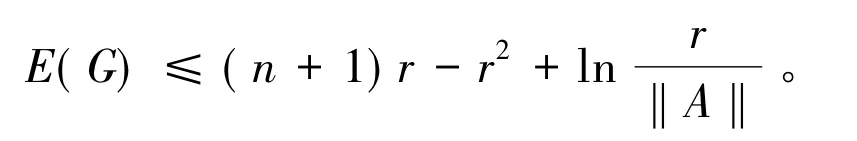
证明 构造函数f(x)=x2－x－ln x，则f'(x)=当x＞1时，f'(x)＞0，函数为增函数，f(x)＞f(1)=0。所以，x＜x2－ln x。因此，循环图G的能量为

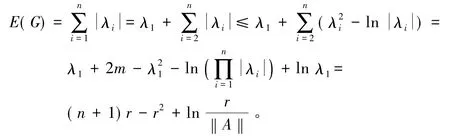
举例说明。设3－循环图G=C(10，{1，5，9})，直接利用软件mathematica计算，得其特征值:

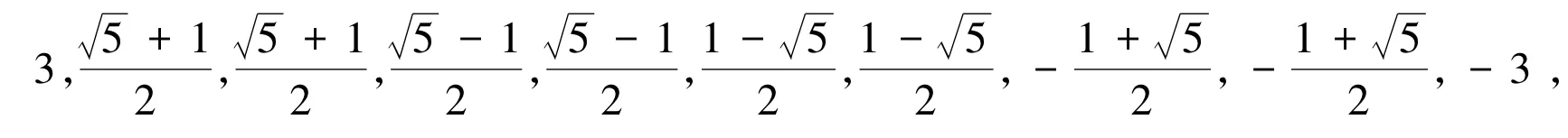
其能量为E(G)=14.94。若按定理1计算，有E(G)≤20.13，定理1显然成立。

定理2 设G是具有n个顶点，度为r的循环图，则

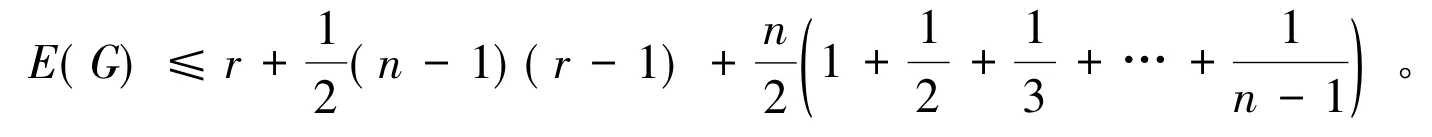
证明 因为G是一个度为r的循环图，所以，nr=2m，并且λ0=r。

根据引理1，有

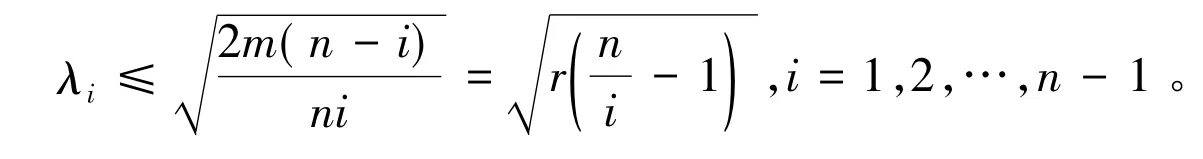
于是有

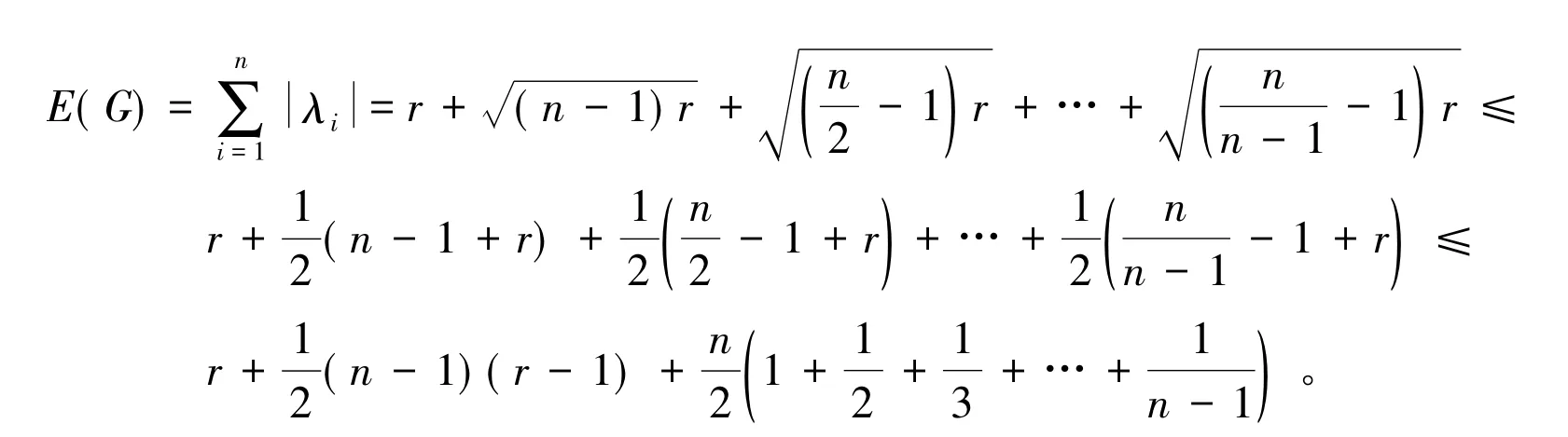
仍然以上述例子为例。利用定理2计算，有E(G)≤26.14，显然，定理2成立。定理3 设G是具有n个顶点，度为r的循环图，则

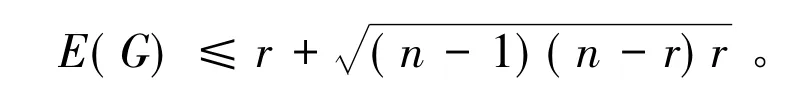
证明 因为G是一个度为r的循环图，所以，d1=d2=… =dn=r，并且nr=2m。根据引理2，有

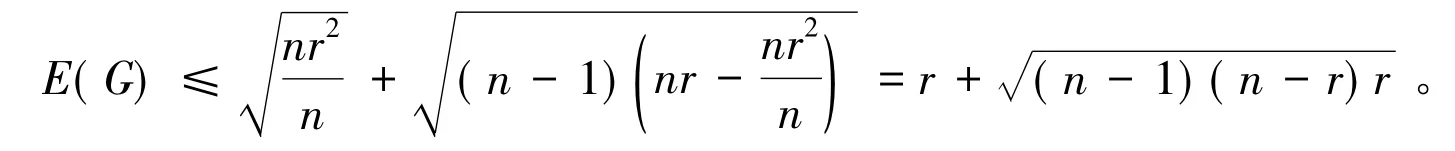
还以上述例子为例。利用定理3计算，有E(G)≤15.73，定理3是成立的。

从上述三个定理及例子来看，定理3的界更接近于实际，要优于定理1和定理2的界。

参考文献:

［1］GUTMAN I.The Energy of a Graph:Old and New Results［J］.Springer Berlin Heidelberg，2001:196－211.

［2］GUTMAN I，RADENKOVIC S，DORDEVIC S，et al.Total π－electron and HOMO energy［J］.Chemical Physics Letters，2016，649:148－150.

［3］GUTMAN I.Total π－electron energy of conjugated molecules with non－bonding molecular orbitals［J］.Zeitschrift für Naturforschung A，2016，71:161－164.

［4］GUTMAN I，RADENKOVIC S，DORDEVIC S，et al.Extending the McClelland formula for total π－electron energy［J］.Journal of Mathematical Chemistry，2017，55(10):1－7.

［5］LI X L，SHI Y T，GUTMAN I.Graph Energy［M］.New York:Spring，2012.

［6］GUTMAN I，FURTULA B.Survey of graph energies［J］.Mathematics Interdisciplinary Research，2017，2:85－129.

［7］MILOVANOVI'C I，MILOVANOVI'C E，GUTMAN I.Upper bounds for some graph energies［J］.Applied Mathematics and Computation，2016，289:435－443.

［8］NIKIFOROV V.The energy of graphs and matrices［J］.Journal of Mathematical Analysis and Applications，2007，326:1472－1475.

［9］FREITAS M A A，ROBBIANO M，BONIF'ACIO A S.An improved upper bound of the energy of some graphs and matrices［J］.MATCH Communications in Mathematical and in Computer Chemistry，2015，74:307－320.

［10］MCCLELLAND B J.Properties of the latent roots of a matrix:The estimation of π－electron energies［J］.The Journal of Chemical Physics，1971，54:640－643.

［11］KOOLEN J，MOULTON V.Maximal energy graphs［J］.Advances in Applied Mathematics，2001，26:47－52.

［12］KOOLEN J，MOULTON V.Maximal energy bipartite graphs［J］.Graphs and Combinatorics，2003，19:131－135.

［13］PRECIADO VM，JADBABAIE A.From Local Measurements to Network Spectral Properties:Beyond Degree Distributions［J］.Decision ＆ Control，2010，58(08):2686－2691.

［14］SHEELA D，ABINAYA S，ANGELO V G，et al.Performance Evaluation of Survivability in Optical Networks Based on Graph Theory［J］.International Journal of Scientific ＆ Engineering Research，2014，5(04):2229－2253.

［15］DAVIS P J.Circulant matrices［M］.New York:John Wiley ＆ Sons，1979.

［16］BRIGHAM R C，DUTTON R D.Bounds on the graph spectra［J］.Journal of Combinatorial Theory，Series B，1984，37:228－234.

［17］ZHOU B.Energy of a graph［J］.MATCH Communications in Mathematical and in Computer Chemistry，2004，51:11－118.