基于代理模型的高效全局低音爆优化设计方法

乔建领，韩忠华，宋文萍

西北工业大学 航空学院 翼型叶栅空气动力学国家级重点实验室，西安 710072

第一代超声速客机商业运营的失败，很大程度上是由音爆噪声等环境问题造成的。随着航空科学技术的进步，20世纪90年代中后期又掀起了一轮低音爆超声速客机研究热潮。发展新一代低音爆超声速客机主要面临两个关键问题：超声速飞行过程中地面音爆强度计算和低音爆气动布局优化设计[1]。

音爆是飞行器在超声速飞行时产生的一种特有的声学现象。在超声速飞行条件下，飞机对气流扰动会形成激波和膨胀波；激波和膨胀波在传播过程中经过演化、汇聚、耗散等作用后传至地面时，人们会听到类似“爆炸”的声音。在对音爆进行研究时，一般将音爆从飞机到地面的传播过程分为近场、中场和远场。其中，远场(地面)音爆强度水平是超声速飞机设计中最须关注的问题之一。国外从20世纪50年代开始，对音爆现象作了系统性研究，发展了基于线化理论的音爆预测方法[2-6]、简化音爆预测方法[7]、波形参数法[8]和Burgers方程法[9]。近年来，随着计算流体力学(CFD)技术的发展，CFD被应用于音爆预测。目前国外学者发展了CFD与波形参数法[10]、全流场CFD求解法[11]和CFD与Burgers方程匹配法[12-13]。针对音爆预测方法，国内研究人员也开展了大量研究[1, 14-16]。

低音爆气动布局优化设计是通过优化算法得到音爆响应较低的外形。冯晓强等[17]运用遗传算法开展了机体容积和音爆响应的多目标优化研究，并得到考虑音爆响应的多目标问题的Pareto解。Choi等[18]在多学科飞机综合分析工具(PASS)基础上通过建立飞行性能和音爆的多可信度响应面模型，并运用单纯形方法(Nelder-Mead Simplex)进行了低音爆超声速公务机的优化。优化过程中以建立的响应面模型代替直接的飞行性能分析和音爆分析，从而减少费时的数值分析次数。Chan[19]在其博士论文中运用多目标遗传算法等优化方法，对两款超声速公务机进行了低阻力和低音爆的优化设计。Farhat等[20]将Whitham修正线化音爆预测理论与梯度优化算法相结合，发展了适用于超声速客机的快速低音爆优化设计方法。Aftosmis等[21]将基于Adjoint的梯度优化方法应用于低音爆优化设计，完成了湾流公司超声速公务机的优化设计，地面音爆响应降低了约10 dB。Wintzer和Kroo[22]也将Adjoint的梯度优化方法应用于低音爆优化设计，完成了低音爆公务机的概念设计。Rallabhandi[23-24]推导出耦合CFD近场计算与基于Burgers方程远场传播模型的伴随方程，并应用到超声速客机的低音爆优化设计中。

由上述文献调研可知，在低音爆优化设计领域，遗传算法等启发式优化和基于Adjoint的梯度优化是目前应用较多的方法[17-27]。遗传算法等启发式优化算法虽然具有全局优化能力，但是优化效率低，在引入高精度的音爆预测方法(需要求解CFD)时，其计算量难以承受。而梯度优化方法虽然效率高，但属于局部优化，优化结果依赖于起始点的选择。

为了解决低音爆优化中全局性和高效性难以兼顾的问题，本文将最新发展的代理优化(Surrogate-Based Optimization, SBO)算法应用于低音爆优化设计，发展了一种高效全局的低音爆优化设计方法。其中，远场音爆分析可采用高精度的方法，但为了方便研究代理优化在低音爆领域的应用潜力，本文采用Whitham方法对远场音爆强度进行分析。选取NASA圆锥体模型对低音爆优化方法进行验证，并与梯度优化和遗传算法的结果进行比较，之后将该方法应用于2014年音爆预测大会翼身组合体标模的低音爆优化设计，展示了该方法在复杂外形低音爆优化设计方面的潜力。

1 音爆预测方法

Whitham发展的线化音爆预测理论是根据超声速旋成体理论修正得到的(本文称为“Whitham理论”)，不用求解流场，计算简单、速度快，计算结果精度比较合理，很适合于飞机初步设计阶段的低音爆布局优化和低音爆优化方法研究。Whitham理论详细推导过程参见文献[2]。

1.1 线化音爆预测理论

Whitham将线化超声速细长旋成体理论中特征线是相互平行的假设进行非线性修正，给出精度较高的特征线描述，获得用于计算近场压强信号和远场音爆强度的公式。其中，计算近场压强信号的公式为

(1)

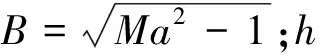
(2)

其中：S″(ξ)为轴向站位ξ处马赫锥所截有效截面积对ξ的二阶导数；y为特征线相关参数[2]。

近场压强信号在向远场传播的过程中，由于激波的汇聚，扰动压强在一定条件下会在远场形成N型波。远场N型波强度的计算公式为

(3)

式(3)为自由空间中过压值的计算式，当观测点位于地面时，考虑地面反射效应因子KR，有

(4)

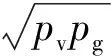
1.2 算例验证

根据线化音爆预测方法开发了相应程序，并选取NASA多段圆锥体模型的试验数据[28]进行验证。图 1为模型示意图，其半径公式为

r=

(5)

式中：l=2 in(1 in≈2.54 cm)；x为圆锥体轴向坐标。

计算时来流马赫数分别为1.26、1.41和2.01，近场音爆信号的观测位置为模型正下方离轴线h=10l处(见图 2)。图 3为应用线化音爆预测方法计算的近场压强信号与试验值的对比。由计算结果与试验值的对比可知，虽然较高马赫数下(图 3(c))的计算结果与试验值还存在一定误差，但总体而言，3种状态下计算值与试验值均吻合较好，验证了本文开发的音爆预测程序的正确性。同时可以看到，由于该音爆预测方法没有考虑大气黏性效应，所以图 3中计算所得近场压强信号的后激波过强。

图1 NASA圆锥体模型Fig.1 NASA cone model

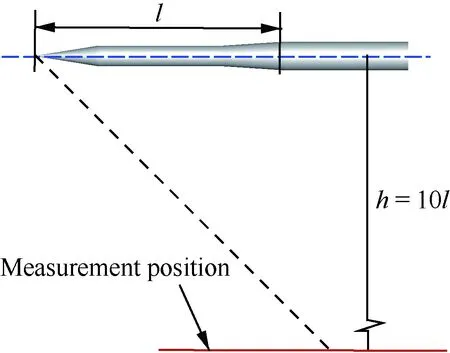
图2 NASA圆锥体模型近场压强信号试验观测位置Fig.2 Experimentally observed position of near-field pressure signature for NASA cone model

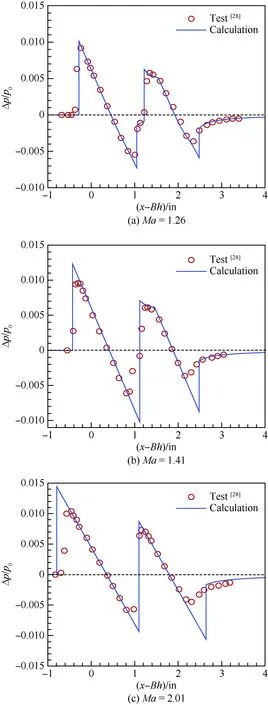
图3 近场压强信号计算值与试验值的对比Fig.3 Comparison between calculation and experimental data of near-field pressure signature

2 代理优化方法及低音爆优化设计

本节概述代理优化方法的几个关键要素和基于代理模型的低音爆优化设计流程。代理优化的关键要素包括试验设计、代理模型及模型训练、优化加点及约束处理、优化收敛判断等，其详细内容见文献[29]。

2.1 试验设计

样本点集是建立代理模型的基础。现代试验设计方法主要有拟蒙特卡洛方法、准蒙特卡洛方法、拉丁超立方抽样(Latin Hypercube Sampling, LHS)、正交试验设计和均匀设计等[30]，其中较为流行的是拉丁超立方和均匀设计方法。本文在进行优化时选择拉丁超立方抽样方法。

2.2 代理模型及模型训练

代理模型是指在分析和优化过程中可“代替”相对复杂和费时的物理分析模型的一种近似数学模型。目前已发展出多种模型，本文在优化过程中选择Kriging模型[31-33]。

Kriging模型将未知函数看作某一高斯随机过程的具体表现，相应随机函数Y(x)的表达式为

Y(x)=β0+Z(x)

(6)

式中：β0为未知函数，是Y(x)的数学期望；Z(x)为均值为0、方差为σ2的静态随机过程。

Kriging模型的具体建模过程详见文献[29]。建模过程涉及相关函数的选择和计算，本文选择的相关函数为“三次样条函数”，其表达式为

Rk(θk,x(i)-x(j))=

(7)

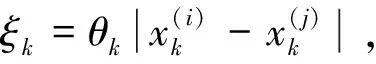
2.3 优化加点准则

优化加点准则是指根据所建立的代理模型增加新样本点的准则。加点的目的是扩充样本集合，提高代理模型的预测精度。代理优化的本质是采用某种加点准则产生新样本点，并使这些样本点逐步落入最优点或其附近。目前已经有多种加点准则，较为流行的有EI(Expected Improvement)准则、MSP(Minimum of Surrogate Prediction)准则、MSE(Mean Squared Error)准则、LCB(Lower Confidence Bounding)准则和PI(Probability of Improvement)准则等[34-36]。本文选择“EI+MSP”的组合加点准则。

2.4 优化收敛判断条件

本文综合采用文献[29]中所述的4种判断方法进行优化收敛判断。

2.5 低音爆优化设计流程

将代理优化方法应用于低音爆优化设计，以提高低音爆优化的效果和效率，特别是当远场音爆计算方法涉及流场求解时其效果更为显著。图4为运用代理优化方法进行低音爆优化设计的流程，低音爆优化方法不单指前面介绍的Whitham理论，也可以是其他精度较高的远场音爆预测算法。本文为方便验证代理优化应用于低音爆优化的可行性和应用于复杂外形低音爆优化的潜力，选择计算速度高、精度可接受的Whitham理论进行远场音爆分析。在低音爆优化过程中，可将远场N型波峰值或远场感觉声压级作为优化目标，对飞机外形进行优化设计[22, 24-26]。

图4 基于代理模型的低音爆优化设计流程Fig.4 Framework of surrogate-based low boom optimization design

3 代理优化应用于低音爆优化设计的算例

本节将代理优化方法应用于NASA圆锥体模型和2014年音爆预测大会翼身组合体标准模型的低音爆优化设计。以NASA圆锥体优化算例来验证代理优化应用的适用性和优越性，以翼身组合体优化算例来说明代理优化在低音爆优化领域的应用潜力。

3.1 NASA圆锥体模型的低音爆优化

3.1.1 外形参数化及优化数学模型

以1.2节中的NASA圆锥体模型(图 1)为基准外形进行低音爆优化设计。外形参数化及优化问题的数学模型建立过程如下。

圆锥体模型参数化如图 5所示。r1、r2分别表示头部圆锥体的最大半径和整个模型的最大半径，l1、l2、l3分别表示NASA圆锥体模型头部圆锥体长度、中间圆柱长度和后部圆台长度。模型参数化后，其半径沿轴向的分布为

(8)

表1为表征NASA圆锥体模型的5个参数的取值范围。

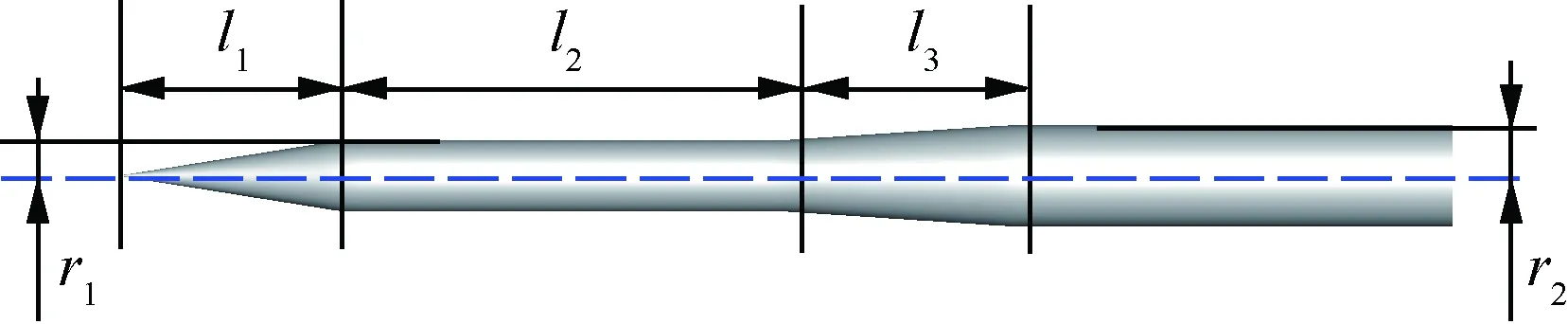
图5 NASA多段圆锥体模型参数化示意图Fig.5 Sketch of parameterization of NASA stepped cone model

表1NASA圆锥体模型低音爆优化设计变量的取值范围

Table1RangeofdesignvariablesforlowboomoptimizationdesignofNASAconemodel

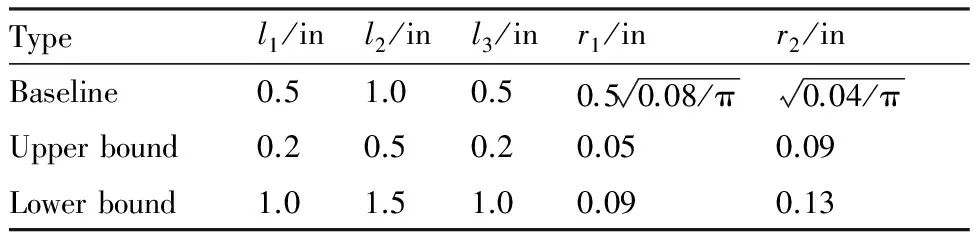
Typel1/inl2/inl3/inr1/inr2/inBaseline0．51．00．50．50．08/π0．04/πUpperbound0．20．50．20．050．09Lowerbound1．01．51．00．090．13

优化设计的目标函数为远场(h/l=1 000，见图 6)音爆N型波的峰值，3种设计状态的来流马赫数分别为1.26、1.60和2.00。相应的数学模型为

(9)

式中：V0=0.038 047 in3为基准模型的体积。前2个约束(C1、C2)为多段圆锥体的长度约束；最后1个约束(C3)为体积约束，以保证l1、l2、l3三段总体积不减。

图6 NASA圆锥体模型低音爆优化中远场N型波的计算位置Fig.6 Calculated position of far-field N-wave for low-boom optimization of NASA cone model

3.1.2 低音爆优化设计结果

低音爆优化设计流程是在课题组开发的代理优化软件SurroOpt[37]上，结合1.1节中介绍的线性音爆预测方法建立的。优化过程中，采用LHS试验设计得到20个初始样本点，并建立Kriging模型，加点准则为“EI+MSP”组合加点，最大样本点个数为300。3种设计状态的收敛历程如图 7所示，图中纵坐标“Obj”为优化目标响应值，横坐标“Evaluation”为音爆分析次数,“DoE”表示通过试验设计获得的初始样本点。

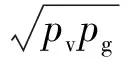
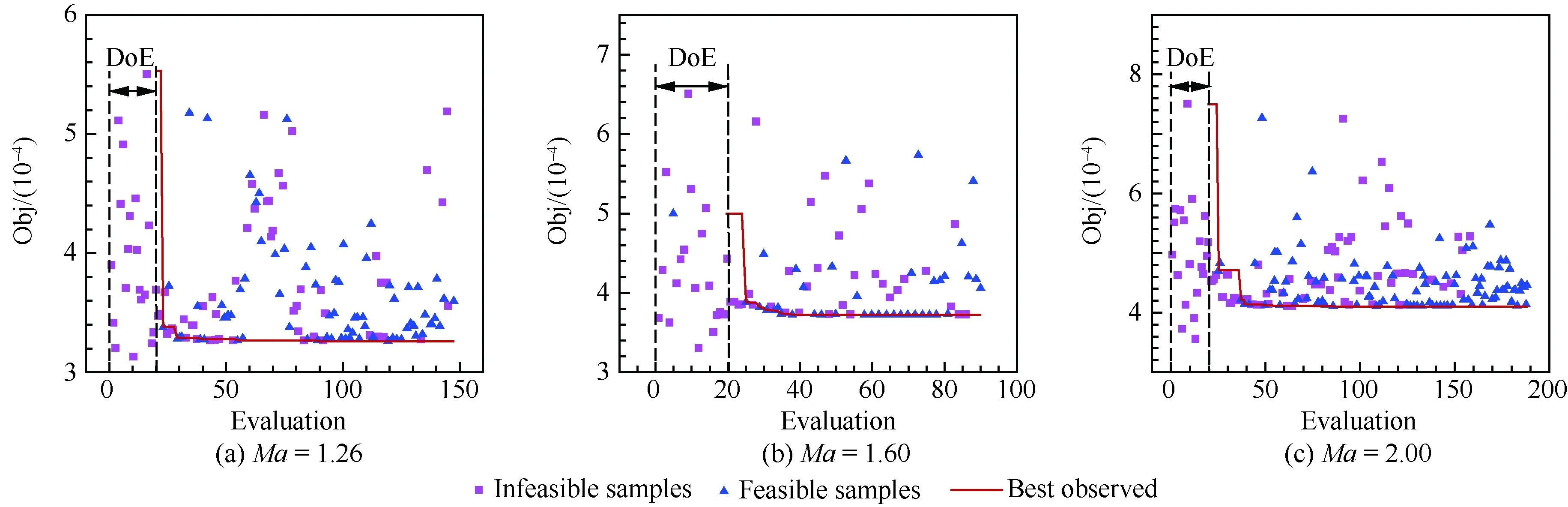
图7 3种设计状态下NASA圆锥体模型低音爆优化设计中目标函数的收敛历程Fig.7 Convergence histories of objective function values at three design states for low boom optimization design of NASA cone model

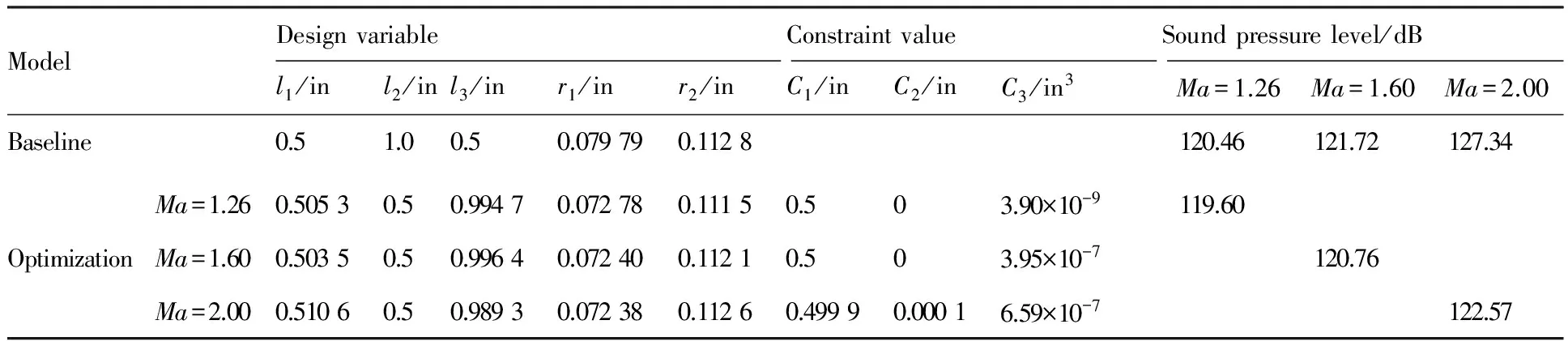
表2 优化前后NASA圆锥体模型的设计变量及远场声压级对比Table 2 Comparison of design variables and far-field sound pressure levels between baseline and optimal NASA cone models

注：表中数据为四舍五入后的值；约束≥0表示满足约束，当约束=0时，表示该约束为主动约束。

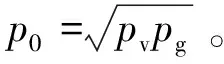
3.1.3 代理优化、梯度优化和遗传算法的结果对比

为说明代理优化算法在低音爆优化设计领域中应用的优越性，分别采用遗传算法和梯度优化算法(序列二次规划(SQP)[38])对Ma=1.26状态下的NASA圆锥体模型进行低音爆优化设计，并与代理优化结果进行对比。遗传算法的种群规模为500，最大进化代数为100，交叉概率为0.9，变异概率为0.05。由于梯度优化算法的优化结果与起始点的选择密切相关，在运用SQP算法进行低音爆优化时，考虑基准外形、最优外形附近及其他位置选取了4个起始点(分别记为x1、x2、x3、x4)，其具体取值及相应点处的约束和目标函数值如表 3所示。表 4为代理优化结果与遗传算法和SQP算法的优化结果对比，“SQP+xi”表示以xi(i=1,2,3,4)为起始点的SQP算法，最右边一列中“147f”表示147次的目标函数计算，“127g”表示127次的目标函数梯度计算。

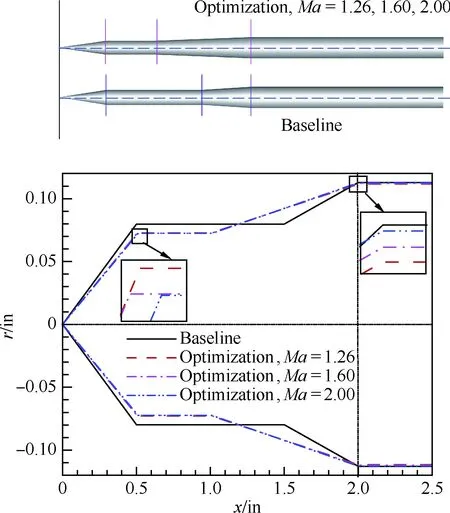
图8 3种设计状态下NASA圆锥体模型优化前后的外形对比Fig.8 Comparison of geometries between baseline and optimal NASA cone models at three design states

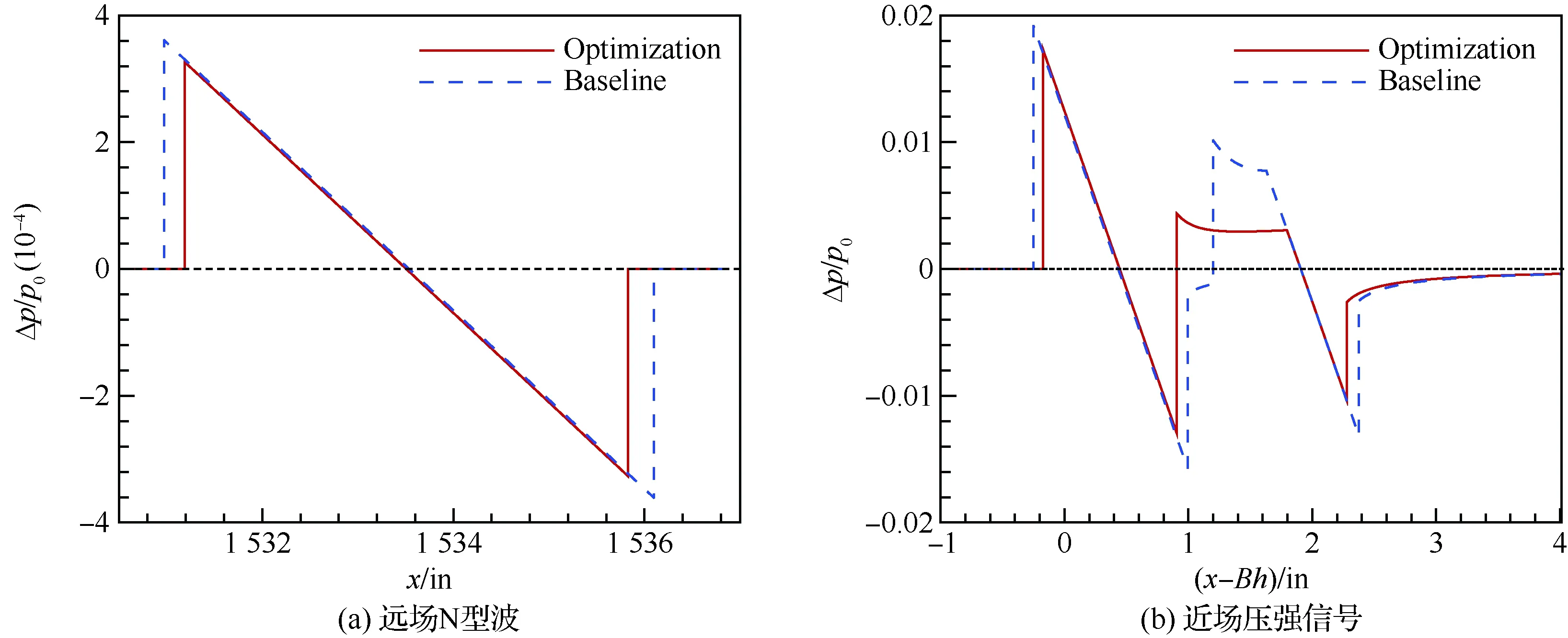
图9 优化前后NASA圆锥体模型的远场N型波和近场压强信号对比(Ma=1.26)Fig.9 Comparison of far-field N-wave and near-field pressure signatures between baseline and optimal NASA cone models (Ma=1.26)

图10 优化前后NASA圆锥体模型的远场N型波和近场压强信号对比(Ma=1.60)Fig.10 Comparison of far-field N-wave and near-field pressure signatures between baseline and optimal NASA cone models (Ma=1.60)

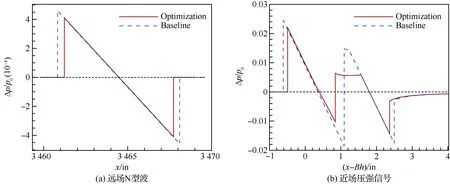
图11 优化前后NASA圆锥体模型的远场N型波和近场压强信号对比(Ma=2.00)Fig.11 Comparison of far-field N-wave and near-field pressure signatures between baseline and optimal NASA cone models (Ma=2.00)

由表 3和表 4可知，针对该低音爆优化设计问题，SQP算法的优化结果在一定程度上依赖于起始点的选择，起始点不同，优化解不同。分别以基准外形(x1)和最优外形附近点(x4)为起始点时，远场音爆N型波强度基本降低到了最低水平；而以其他位置(x2和x3)为起始点时，优化外形相对于基准外形的远场音爆N型波强度虽然都有不同程度的减弱，但都没有达到全局最优。出现这一现象的原因是设计空间内存在多极值，梯度优化易陷入局部最优。此外，由表 4可知，遗传算法虽然具有全局优化能力，但在优化过程中需要大量的目标函数计算，造成巨大的信息浪费，因此其优化效率很低。

综上所述，与梯度优化相比，代理优化算法的结果不依赖于起始点的选择，能够获得全局最优解；而与遗传算法相比，代理优化算法的效率高了2个量级以上。结果表明，代理优化算法在低音爆优化设计领域中具有明显的优势。

表3 SQP算法起始点位置的约束和目标函数值Table 3 Constraints and objective function values at start points of SQP algorithm

注：x1为基准外形点，x4为最优外形附近点，x2、x3为其他位置点。

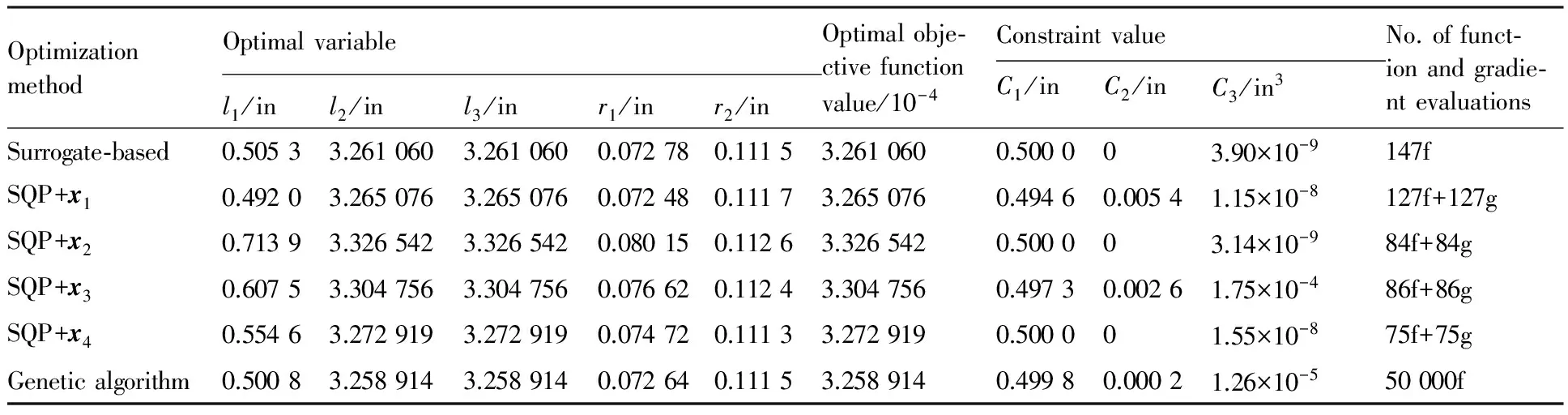
表4 3种优化算法对相同低音爆优化问题的优化结果对比Table 4 Comparison of results of three optimization algorithms for same low boom optimization problem

3.2 翼身组合体外形的低音爆优化

2014年1月，AIAA第1届音爆预测大会在美国马里兰州举行，旨在评估和探讨近场音爆水平的预测技术[39]。为方便研究不同音爆预测方法之间的差异，大会给出3个标准模型，分别为NASA圆锥体、三角翼翼身组合体(69° DWB)以及洛克希德·马丁的超声速客机模型(LM1021)，其中前2个模型为无升力模型[40]。69° DWB外形是Hunton等[41]研究不同翼面形状对音爆影响所用的模型之一，图 12为模型示意图，模型全长17.52 cm，机头长7.01 cm，机头母线沿飞机轴向符合二次函数分布，机身最大半径为0.54 cm，三角翼的前缘后掠角为69°，三角翼翼型为菱形翼型，其最大厚度为弦长(c)的5%。

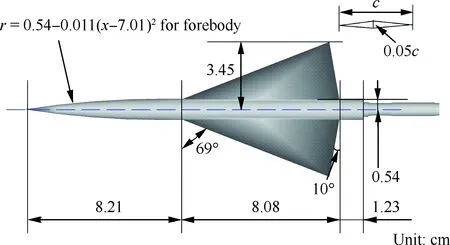
图12 69°后掠三角翼翼身组合体标准模型示意图Fig.12 Sketch of 69° sweepback delta wing-body configuration standard model

大会给出的69°后掠三角翼翼身组合体标模的状态为Ma=1.7,迎角α=0°，来流雷诺数Re=2.43×106，采用Whitham理论对模型中心线正下方h=62.99 cm处的压强信号进行计算，计算结果与试验值[42]的对比如图 13所示。

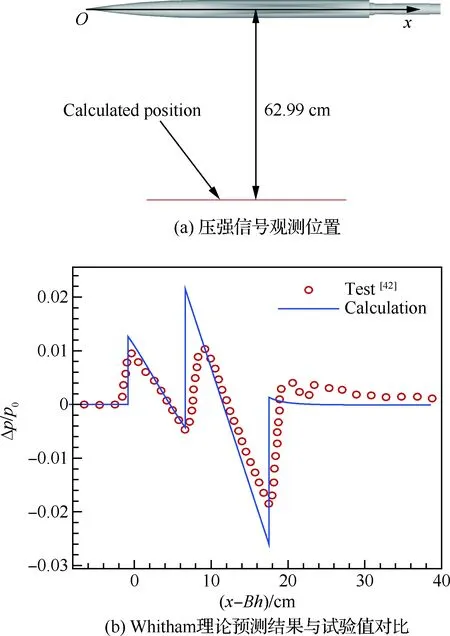
图13 翼身组合体近场压强信号计算验证Fig.13 Calculation verification of near-field pressure signatures for wing-body configuration

3.2.1 外形参数化与优化数学模型

机翼参数化如图 14所示。为保证三角翼和菱形翼型特征，机翼控制参数为：机翼1/2弦线后掠角Λ1/2、翼根翼型的弦长c、翼根翼型最大厚度与弦长的比值t、机翼半展长b和机翼位置lw共5个参数。

机身参数化如图 15所示，通过对机身母线的控制来实现。机身母线采用Bezier曲线进行参数化，共选取10个控制点，坐标为(xi,Bi)。xi为第i个控制点的轴向站位(图15(a)),在母线参数化和低音爆优化过程中保持不变。Bi为第i个控制点的纵坐标(图15(b))，是母线参数化和低音爆优化的变量。

采用Whitham理论计算远场音爆强度，优化时目标为Ma=1.7状态下飞机轴线正下方1 000倍机长处N型波的压强峰值，由于模型为对称模型，因此在优化过程中不考虑升力约束。相应优化问题的数学模型如下

(10)

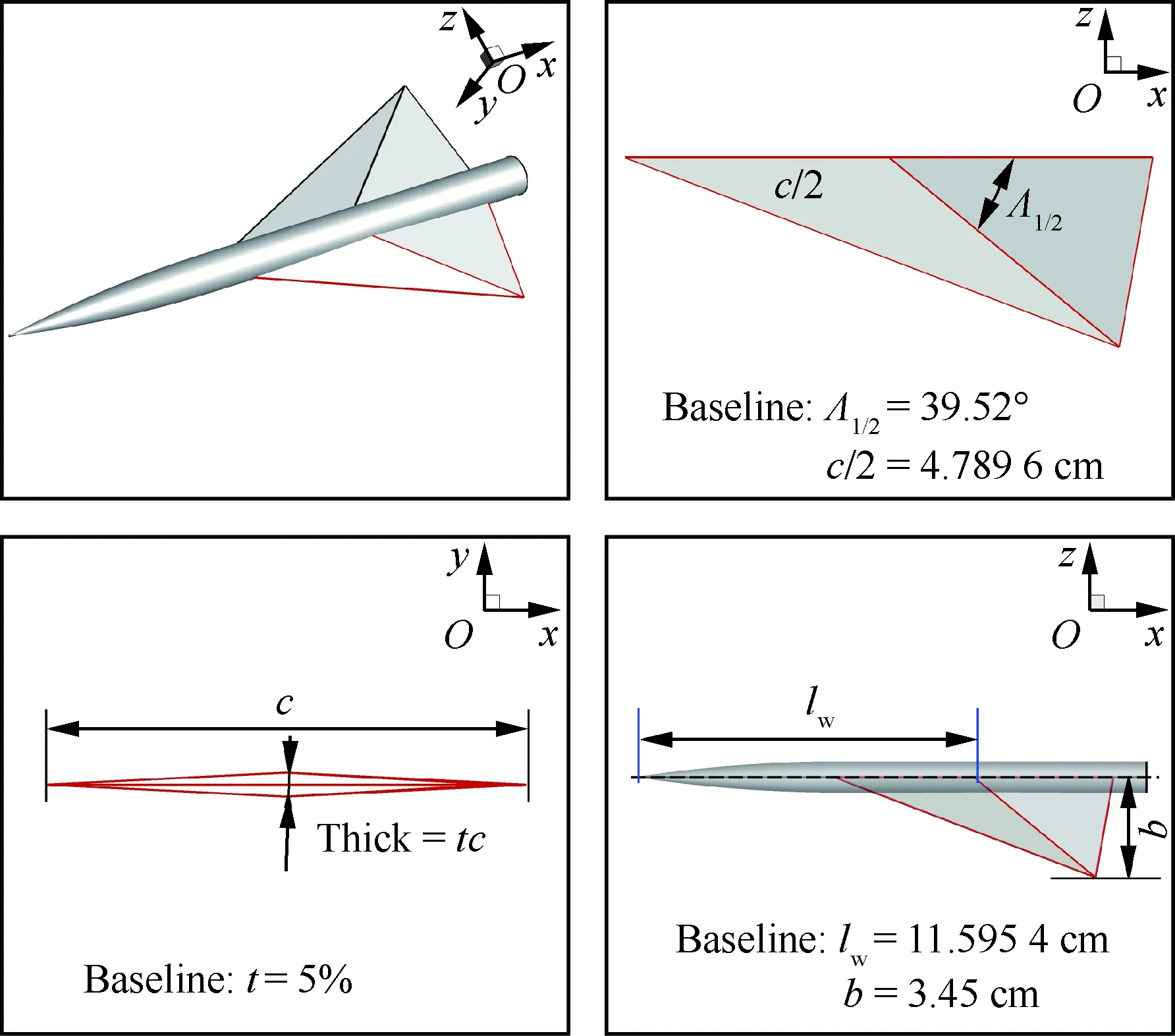
图14 翼身组合体的机翼参数化示意图Fig.14 Sketch of wing parameterization of wing-body configuration

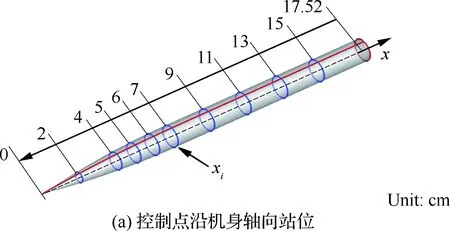
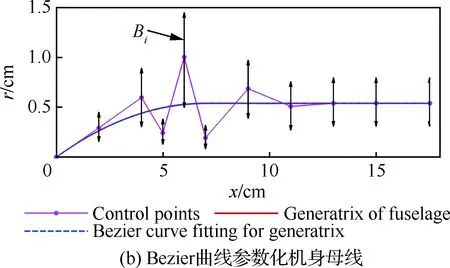
图15 翼身组合体的机身母线参数化示意图Fig.15 Sketch of fuselage generatrix parameterization of wing-body configuration

式中：Vf、Vf,0分别为外形优化后机身容积和基准机身容积；Vw、Vw,0分别为外形优化后机翼容积和基准机翼容积；lf,0为基准机身长度；Sw、Sw,0分别为优化后机翼面积和基准机翼面积。

控制翼身组合体外形的15个设计变量的取值范围如表 5所示。控制机翼的5个参数的取值范围为基准参数的(1±0.2)倍。控制机身的10个参数的取值范围为基准参数的(1±0.5)倍，图15(b)中控制站位处箭头长短代表了相应控制点可移动的范围大小，图 16给出了机身母线能够变化的范围。

3.2.2 低音爆优化结果

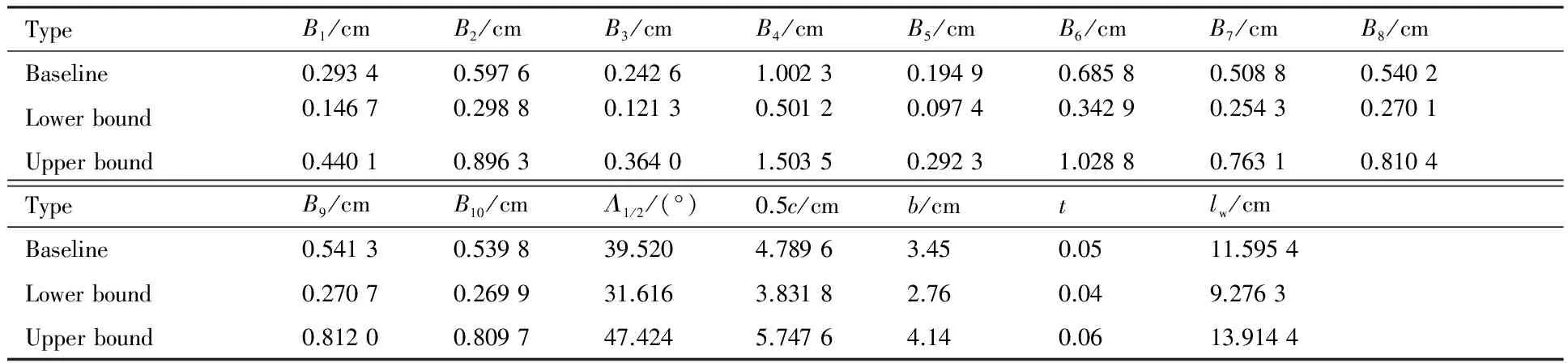
表5 翼身组合体设计变量及设计空间Table 5 Design variables and design space of wing-body configuration

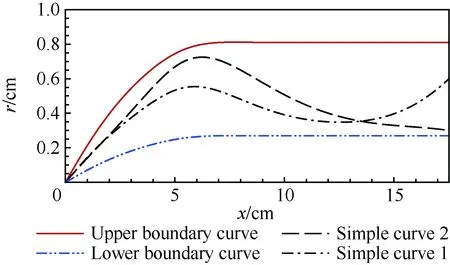
图16 翼身组合体机身母线变化的范围以及范围内的两条曲线Fig.16 Variation range of fuselage generatrix of wing-body configuration and two curves within the range

图19和图 20分别给出优化前后的外形对比和优化前后的机身母线对比。可以看出，优化后机翼的后掠角变大，翼展略有减小，在机身与机翼结合部位，机身的半径变小，同时为保证机身容积约束，机头处半径变大。这样的布局形式可以使飞机在巡航状态(Ma=1.7)下，具有低音爆的有效截面积分布。图 21给出了优化前后的有效截面积(Seff)分布，可知优化外形的有效截面积分布在机头处斜率增大，随后变化平缓且最大有效截面积减小，使得近场压强信号表现为第1道激波略有增强，第2道激波明显减弱，且两道激波之间距离增大，图 22为优化后的近场(h=62.99 cm)压强信号。当这样的近场压强信号传播到远场时，第1道激波与第2道激波合并，使N型波的峰值减小，从而达到降低音爆强度的目的。

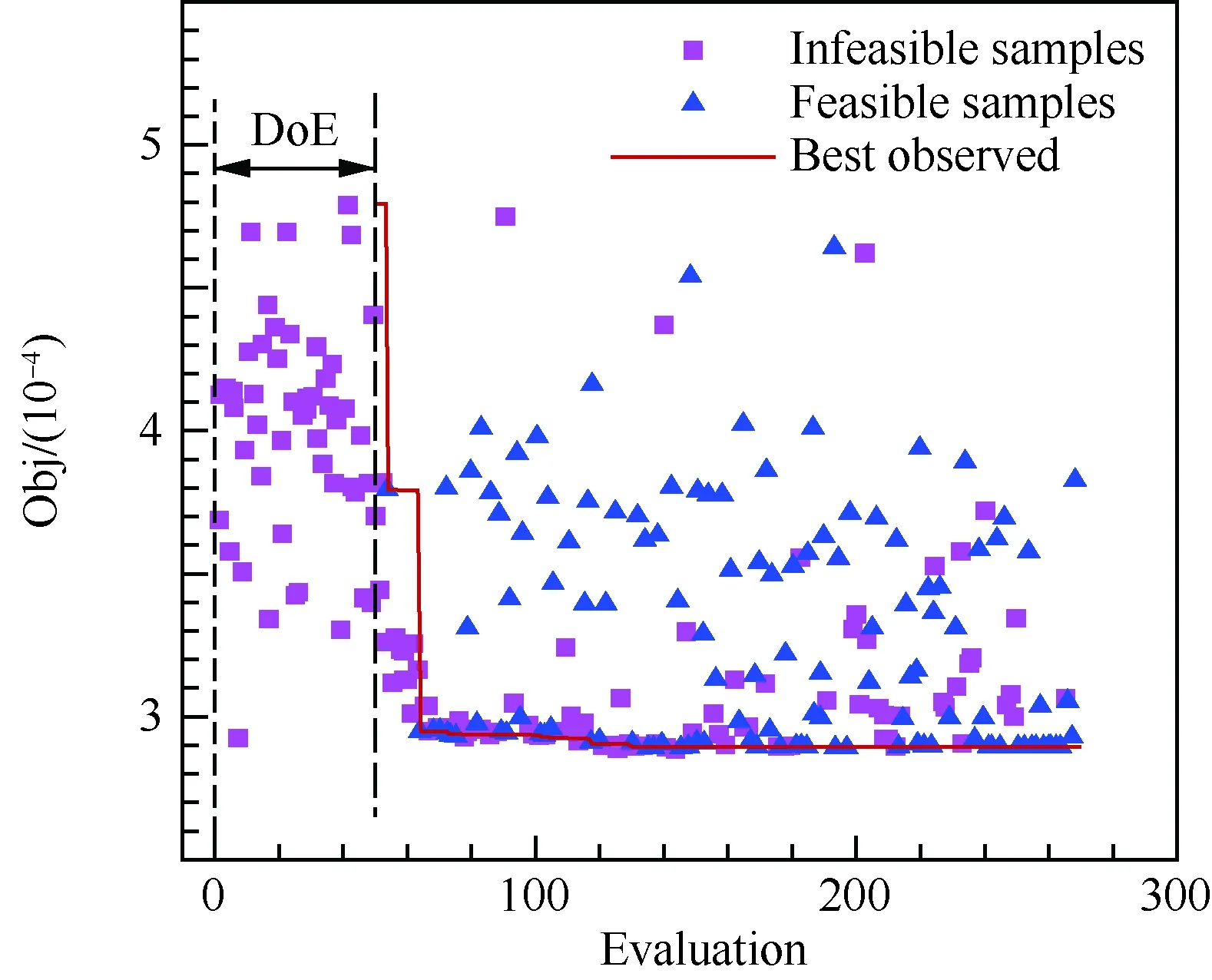
图17 翼身组合体低音爆优化的收敛历程Fig.17 Convergence history of low boom optimization for wing-body configuration

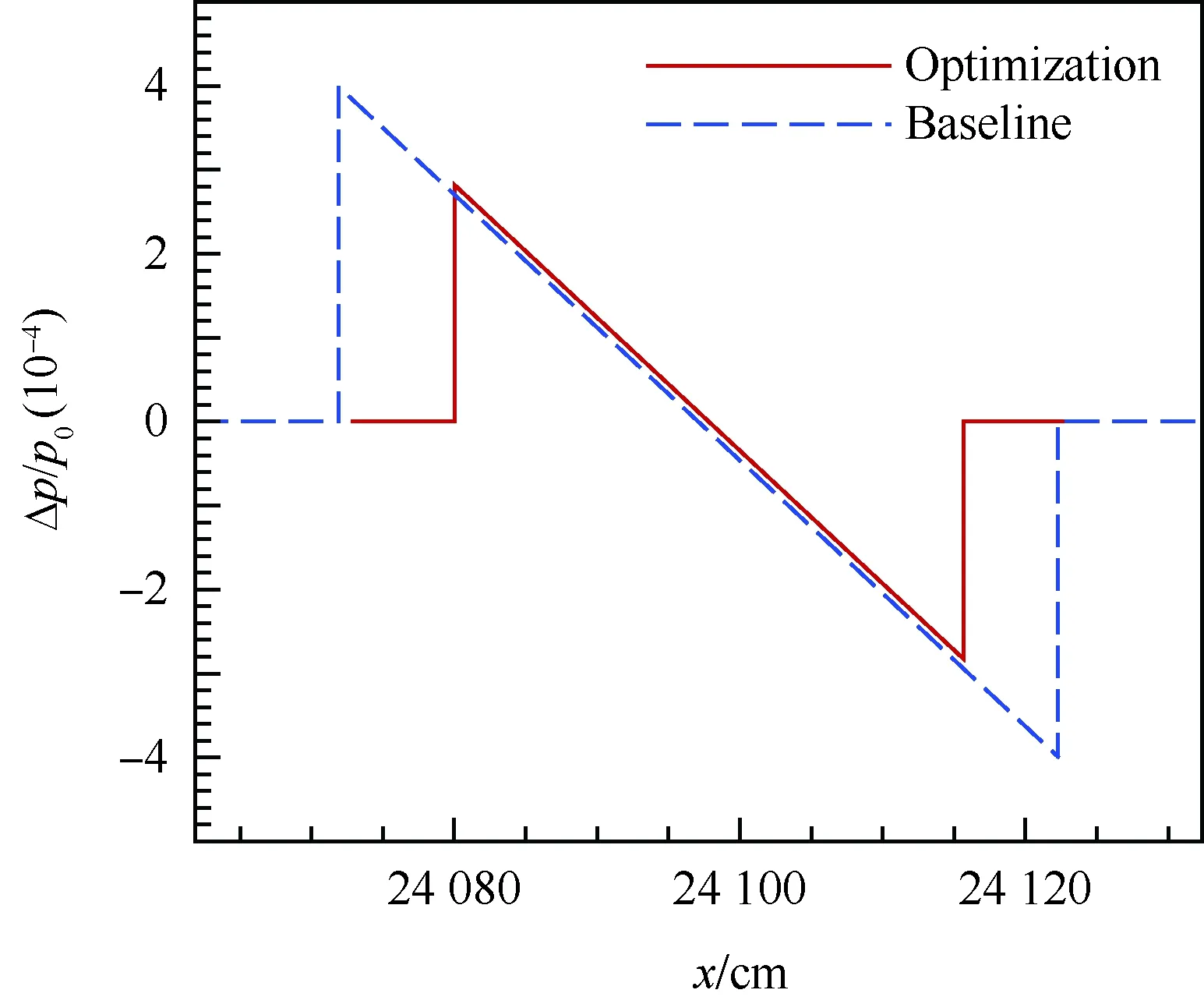
图18 翼身组合体优化前后远场N型波对比Fig.18 Comparison of far-field N-wave between baseline and optimal wing-body configurations

表6 翼身组合体优化前后参数对比Table 6 Comparison of parameters between baseline and optimal wing-body configurations

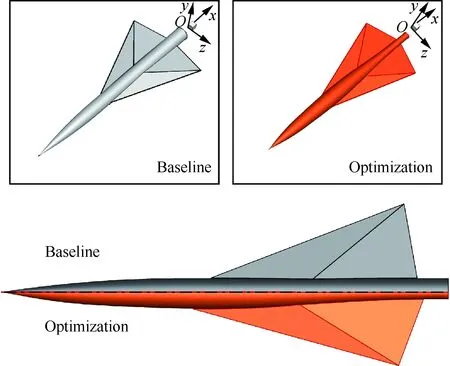
图19 翼身组合体优化前后外形对比Fig.19 Comparison of geometries between baseline and optimal wing-body configurations

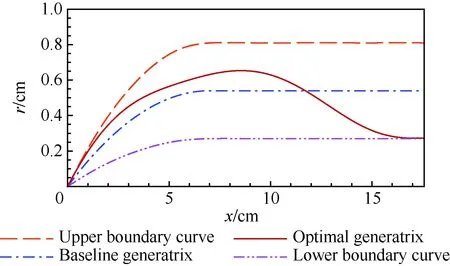
图20 翼身组合体优化前后的机身母线对比Fig.20 Comparison of fuselage generatrix between baseline and optimal wing-body configurations

图21 翼身组合体优化前后有效截面积分布对比Fig.21 Comparison of effective cross-section distribution between baseline and optimal wing-body configurations

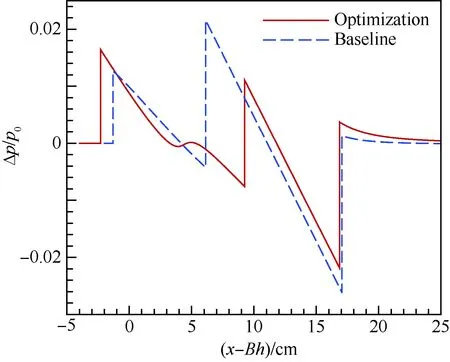
图22 翼身组合体优化前后近场压强信号对比Fig.22 Comparison of near-field pressure signature between baseline and optimal wing-body configurations

4 结 论

本文将代理优化应用于飞行器的低音爆优化设计，发展了一种基于代理模型的低音爆优化设计方法。

1) 用本文方法进行了NASA圆锥体模型的低音爆优化设计，3种优化设计状态下，远场音爆强度相比于基准外形降低了近1 dB，表明该方法应用于低音爆优化设计的可行性。

2) 针对NASA圆锥体模型的低音爆优化设计，代理优化方法相比于梯度优化和遗传算法，具有很好的优越性。与梯度优化结果相比具有全局性，与遗传算法相比具有高效性。

3) 将代理优化方法应用于翼身组合体外形的低音爆优化设计，优化后的模型更具有低音爆的特征，远场N型波峰值减少了27.4%，表明本文方法在复杂外形低音爆优化设计中具有很大的应用潜力。

本文的重点是展示基于代理模型的全局优化方法在低音爆优化设计中的适用性，并为进一步研究打下基础。一方面，本文选择了计算效率高、计算精度合理的Whitham方法来预测远场音爆。这种方法对于复杂外形的适应性和音爆预测精度都存在一定的不足，下一步拟发展耦合高可信度CFD和非线性Burgers方程的高精度音爆预测方法。另一方面，本文优化没有考虑气动性能的目标和约束。为了增强设计结果的工程适用性，下一步需要在优化中考虑气动性能的目标(如升阻比或阻力)和约束(如升力和力矩)。

参 考 文 献

[1] 朱自强, 兰世隆. 超声速民机和降低音爆研究[J]. 航空学报, 2015, 36(8): 2507-2528.

ZHU Z Q, LAN S L. Study of supersonic commercial transport and reduction of sonic boom[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2507-2528 (in Chinese).

[2] WHITHAM G. The flow pattern of a supersonic project[J]. Communications on Pure and Applied Mathematics, 1952, 5(3): 301-347.

[3] HAYES W D. Brief review of basic theory: Sonic boom research: NASA SP-147[R]. Washington, D.C.: NASA, 1967.

[4] SEEBASS R. Sonic boom theory[J]. Journal of Aircraft, 1969, 6(3):177-184.

[5] SEEBASS R, GEORGE A R. Sonic boom minimization[J]. Journal of the Acoustical Society of America, 1972, 51(2): 686-694.

[6] SEEBASS R, ARGROWB. Sonic boom minimization revisited: AIAA-1998-2956[R]. Reston, VA: AIAA, 1998.

[7] CARLSON H W. Simplified sonic boom prediction: NASA TP-1122[R]. Washington, D.C.: NASA, 1978.

[8] THOMAS L C. Extrapolation of sonic boom pressure signatures by the waveform parameter method: NASA TN D-6832[R]. Washington, D.C.: NASA, 1972.

[9] CLEVELAND O R. Propagation of sonic booms through a real, stratified atmosphere[D]. Austin: University of Texas at Austin, 1995: 6-37.

[10] POTAPKIN A V, KOROTAEVA T A, MOSKVICHEV D Y, et al. Anadvanced approach for far-field sonic boom prediction: AIAA-2009-1056[R]. Reston, VA: AIAA, 2009.

[11] YAMASHITA R, SUZUKI K. Full-field sonic boom simulation in real atmosphere: AIAA-2014-2269[R]. Reston, VA: AIAA, 2014.

[12] WINTZER M, NEMEC M, AFTOSMIS J M. Adjoint-based adaptive mesh refinement for sonic boom prediction: AIAA-2008-6593[R]. Reston, VA: AIAA, 2008.

[13] RALLABHANDI S K. Advanced sonic boom prediction using the augmented Burgers equation[J]. Journal of Aircraft, 2011, 48(4): 1245-1253.

[14] 陈鹏, 李晓东. 基于Khokhlov-Zabolotskaya-Kuznetsov方程的声爆频域预测法[J]. 航空动力学报, 2010, 25(2): 359-365.

CHEN P, LI X D. Frequency domain method for predicting sonic boom propagation based on Khokhlov-Zabolotskaya-Kuznetsov equation[J]. Journal of Aerospace Power, 2010, 25(2): 359-365 (in Chinese).

[15] 但聃, 杨伟. 超音速公务机声爆计算与布局讨论[J]. 航空工程进展, 2012, 3(1): 8-15.

DAN D, YANG W. Supersonic business jet sonic boom computation and layout discussion[J]. Advances in Aeronautical Science and Engineering, 2012, 3(1): 8-15 (in Chinese).

[16] 冯晓强. 声爆计算方法研究及在超声速客机设计的应用[D]. 西安: 西北工业大学, 2012: 9-24.

FENG X Q. The research of sonic boom prediction method and application in supersonic aircraft design[D]. Xi’an: Northwestern Polytechnical University, 2012: 9-24 (in Chinese).

[17] 冯晓强, 宋笔锋, 李占科, 等. 超声速飞机低声爆布局混合优化方法研究[J]. 航空学报, 2013, 34(8): 1768-1777.

FENG X Q, SONG B F, LI Z K, et al. Hybrid optimization approach research for low sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1768-1777 (in Chinese).

[18] CHOI S, ALONSO J J, KROO M I. Multi-fidelity design optimization of low-boom supersonic business jets: AIAA-2004-4371[R]. Reston, VA: AIAA, 2004.

[19] CHAN K M. Supersonicaircraft optimization for minimizing drag and sonic boom[D]. Palo Alto: Stanford University, 2003: 48-96.

[20] FARHAT C, MAUTE K, ARGROW B, et al. Shape optimization methodology for reducing the sonic boom initial pressure rise[J]. AIAA Journal, 2007, 45(5): 1007-1018.

[21] AFTOSMIS M J, NEMEC M, CLIFF S E. Adjoint-based low-boom design with Cart3D: AIAA-2011-3500[R]. Reston, VA: AIAA, 2011.

[22] WINTZER M, KROO I. Optimization and adjoint-based CFD for the conceptual design of low sonic boom aircraft: AIAA-2012-0963[R]. Reston, VA: AIAA, 2012.

[23] RALLABHANDI K S. Sonic boom adjoint methodology and its applications: AIAA-2011-3497[R]. Reston, VA: AIAA, 2011.

[24] RALLABHANDI K S. Application of adjoint methodology to supersonic aircraft design using reversed equivalent areas[J]. Journal of Aircraft, 2014, 51(6): 1873-1882.

[25] MINELLI A, SALAH E D I, CARRIER G. Advancedoptimization approach for supersonic low-boom design: AIAA-2012-2168[R]. Reston, VA: AIAA, 2012.

[26] LI J H, TIM W, RAMESH K A. Shapeoptimization of supersonic bodies to reduce sonic boom signature: AIAA-2016-3432[R]. Reston, VA: AIAA, 2016.

[27] LI J H, KRAMPF J, MITCHELL J, et al. Prediction,minimization and propagation of sonic boom from supersonic bodies: AIAA-2017-0277[R]. Reston, VA: AIAA, 2017.

[28] CARLSON H W, MACK R J, MORRIS O A. A wind tunnel investigation of the effect of body shape on sonic boom pressure distributions: NASA TN D-3106[R]. Washington, D.C.: NASA, 1965.

[29] 韩忠华. Kriging模型及代理优化算法研究新进展[J]. 航空学报, 2016, 37(11): 3197-3225.

HAN Z H. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225 (in Chinese).

[30] GIUNTA A A, WOJTKIEWICZ J S F, ELDRED M S. Overview of modern design of experiments methods for computational simulations: AIAA-2003-649[R]. Reston, VA: AIAA, 2003.

[31] KRIGE D G. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the Chemical Metallurgical & Mining Society of South Africa, 1951, 52(6): 119-139.

[32] HAN Z H, GOERTZ S. Hierarchical kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1285-1296.

[33] HAN Z H, ZHANG Y, SONG C X, et al. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization[J]. AIAA Journal, 2017, 55(12): 4330-4346.

[34] FORRESTER A I J, KEANE A J. Recentadvances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79.

[35] JONES D R. Ataxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21(4): 345-383.

[36] LIU J, SONG W P, HAN Z H, et al. Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models[J]. Structural and Multidisciplinary Optimization, 2016, 55(3):925-943.

[37] HAN Z H. SurroOpt a generic surrogate-based optimization code for aerodynamic and multidisciplinary design: ICAS-2016-0281[R]. Bonn: ICAS, 2016.

[38] GILL P E, MURRAY W. NPSOL: AFORTRAN package for nonlinear programming[EB/OL]. (2013-07-15) [2016-07-20]. http:∥www.sbsi-sol-optimize.com.

[39] AFTOSMIS M J, NEMEC M. Cart3D simulations for the first AIAA sonic boom prediction workshop: AIAA-2014-0558[R]. Reston, VA: AIAA, 2014.

[40] DAGRAU F, LOSEILLE A, SALAH E D I. Computational and experimental assessment of models for the first AIAA sonic boom prediction workshop using high fidelity CFD methods with mesh adaptation: AIAA-2014-2009[R]. Reston, VA: AIAA,2014.

[41] HUNTON W L, HICKS M R, MENDOZA P J. Some effects of wing planform on sonic boom: NASA TN D-7160[R]. Washington, D.C.: NASA, 1973.

[42] MA P B, WANG G, REN J, et al. Near field sonic boom analysis with HUNS3D solver: AIAA-2017-0038[R]. Reston, VA, AIAA, 2017.