飞行器气动/结构多学科延迟耦合伴随系统数值研究

黄江涛，周铸,*，刘刚，高正红，黄勇，王运涛

1.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000 2.西北工业大学 翼型叶栅空气动力学国防科技重点实验室， 西安 710072

基于伴随方程的气动优化以其独有的优势，在气动设计等领域扮演着重要角色，也是国内外空气动力学研究机构一个重要的研究方向，而基于变分思想的气动/结构多学科伴随优化方法也开始在工程领域发挥重要作用，例如考虑气动弹性变形的柔性机翼若采用基于差分的梯度优化以及进化算法开展多学科多目标优化，其计算量非常庞大，甚至难以忍受，设计效率极为低下。另一方面，未来飞机发展的一个重要方向是重量较轻的复合材料结构柔性机翼设计(如B787、B747-8等宽体客机)，此时气动、结构耦合效果将更加明显，基于多学科耦合伴随系统的灵敏度分析在综合设计上具有更加突出的优势。针对该研究方向，国外在多学科耦合伴随[1]方面开展了系列的研究，例如密歇根大学Martins教授的多学科优化设计(MDO)团队，基于结构网格CFD求解器以及有限元方法发展了气动/结构延迟耦合伴随(Lagged Coupled Adjoint,LCA)方法，实现了气动结构一体化设计[2-3]，斯坦福大学Jameson团队基于耦合伴随系统进行了机翼平面形状与剖面的气动结构多学科优化[4]，德宇航Abu-Zurayk和Brezillon基于非结构化求解器TAU[5]，以及法宇航Marcelet等基于CFD代码elsA也发展了LCA优化方法[6-7]。

国内在流场单学科离散伴随方程求解器以及基于代理模型的气动/结构多学科优化方面取得了一定的进展[8-14]。大多工作局限于单学科伴随系统以及基于进化算法的优化，在多学科耦合伴随系统自主研发方面研究基础比较薄弱。由于气动/结构耦合伴随系统具有计算代价小，梯度计算量与各个学科设计变量个数均无关等优点，且通过耦合伴随方程的求解能够快速计算出气动、结构等学科关心的各个目标函数对公共设计变量以及独立设计变量的导数，将在未来多学科优化领域发挥重要作用。

由于耦合伴随系统中交叉学科导数项的具体推导方法，耦合方程组对应左端的各个大型稀疏矩阵的求解方式和变分简化处理方式，以及学科之间物理场信息、伴随变量交换方式直接影响了多学科变分的简捷性、耦合系统计算效率与梯度信息的计算精度。因此，本文将对以上几个关键环节的变分推导、各个学科伴随方程的求解方法进行详细系统的研究与改进。基于课题组自主研发的大型并行结构化网格雷诺平均Navier-Stokes (RANS)求解器PMB3D (Paralleized Muti-Block solver for 3-Dimensional flow)[15]以及流固耦合代码FSC3D(Fluid-Solid Coupled platform for 3-Dimensional case)首先建立了飞行器静气动弹性数值模拟技术，进一步基于并行化伴随方程求解器PADJ3D (Paralleized ADJoint solver for 3-Dimensional flow)[16]，开展多学科耦合伴随系统的构建与求解研究，希望能够为多学科耦合伴随系统的研究人员提供有价值的参考。

1 耦合系统中的学科分析代码

1.1 并行化CFD代码PMB3D

PMB3D是课题组自主研发的大型并行CFD代码，求解任意曲线坐标系下的Navier-Stokes方程实现流场精细化数值模拟,即

(1)

PMB3D具备S-A一方程、剪切应力输运(SST)两方程湍流模型以及Langtry-Menter转捩预测模型， Roe、Vanleer等多种空间离散方法，MUSCL(Monotonic Upwind Scheme for Conservation Laws)迎风插值与WENO(Weighted Essentially Non-Oscillatory )格式，隐式时间推进，多重网格技术，支持多块对接、拼接以及重叠网格技术，以及基于MPI(Message Passing Interface)通信协议的大规模并行计算能力，广泛应用于常规气动力计算、多体分离、空中加油安全性分析、进排气系统、旋转部件气动特性计算以及火箭发射、级间分离等领域[15]。

1.2 流固耦合代码FSC3D

FSC3D代码采用虚功原理与径向基函数(RBF)插值技术[17]实现CFD边界面元气动力向结构点、结构点位移向CFD物面格点高精度插值，基于RBF方法的插值技术数学模型表示为

(2)

式中：αi为插值系数;φ(·)为基函数。

本文对p(x)的选取采用多项式方法，即

式中：αi(i=0,1,…,n)为插值系数；xi,n为中心点坐标;M为径向基中心矢量维数。

1.3 静气动弹性数值模拟代码

采用LDLT方法[18]求解结构静力学方程：

Kd=F

(3)

式中：K为刚度矩阵；d为结构节点在6个自由度的变形位移；F为作用在节点上的气动力矩阵。在完成位移耦合即气动表面网格更新后，本文采用径向基结合无限插值技术进行空间网格变形，由上述RBF技术依据物面网格顶点的变形量构建RBF精确插值模型, 操作空间网格Block顶点进行变形插值, 保证网格整体空间拓扑一致性，进一步利用TFI(TransFinite Interpolation)无限插值进行Block中ξ、η、γ3个方向的Edge、Face以及内点更新[19],即

(4)

式中：dx和s、t、u分别为位移以及3个方向上的逻辑坐标；NI、NK、NJ分别代表3个方向的网格维度;Sξ,η,γ、tξ,η,γ和uξ,η,γ代表3个曲线坐标方向。

为了加速静气动弹性数值模拟的收敛速度，本文采用流固耦合计算与CFD求解器共用模块的方式，即在流场迭代至指定步数，利用不完全收敛解进行弹性变形计算，直至流场收敛，如图1所示。

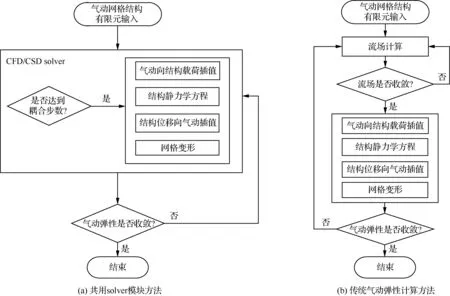
图1 共用solver模块方法与传统气动弹性计算方法流程对比Fig.1 Comparison of process of common solver module method with traditional aeroelasticity calculation method

2 流场伴随方程简介

对于气动优化设计的最小化问题：

minI(w,X,D)

(5)

式中：I可以是升、阻力、力矩、流量、压比等参数；w、X、D分别为流场守恒变量、网格变量、设计变量;在流场收敛解的条件下，残差约束R(w,X,D)=0，引入拉格朗日算子λ构造目标函数，即

L=I+λTR

(6)

对式(6)进行求导，可得

(7)

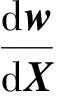
(8)

式(8)就是流场伴随方程，通过隐式迭代方法求解拉格朗日算子λ之后，可以通过式(9)进行目标函数梯度信息快速求解,即

(9)

(10)

本文采用二阶精度的中心格式、人工黏性以及SST两方程湍流模型，手工推导构造Navier-Stokes方程离散伴随方程，并进一步引入虚拟时间项：

(11)

式中：Vj,k,l为网格体积；Rc(λ)、RD(λ)、Rv(λ)j,k,l分别代表伴随方程的对流项、人工黏性项以及物理黏性项。对式(11)的迭代求解，采用LU-SGS方法隐式时间推进，离散伴随方程各项的空间离散采用矩阵形式的物理边界条件，冻结湍流黏性系数，时间推进采用的隐式边界条件为

Δλ*=0, Δλ=0

(12)

式中:λ*为隐式推进的中间项。

黏性项采用薄层近似，曲线坐标系下的黏性通量可以表达为

(13)

式中:各项表达式具体含义可参考文献[16]。

与流场并行计算一样，离散伴随方程求解时，并行机制依然采用单元数衡量的负载平衡、对等式计算以及MPI消息传递模式，对于伴随方程来讲，依赖于求解器的构架，通过MPI进行传递的信息可以是雅克比矩阵，也可以是伴随变量本身。本文求解器采用了多块对接网格技术，与流场对接面边界信息一样，MPI传递的信息是各个进程中分割面上的两层虚网格上的伴随变量信息。

3 考虑结构静力学方程的耦合伴随方程

3.1 耦合伴随方程

参照第2节流场变分思想，综合考虑最小化目标函数、流场收敛解约束以及气动弹性平衡约束，有

minI(w,X,D)

(14)

式中：Ra、Rs分别为流场残差与结构静力学残差；K、d、F分别为结构刚度矩阵、变形位移以及载荷分布。对式(14)引入拉格朗日算子ψ可以构造目标函数：

(15)

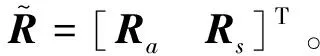
(16)

令式(16)第1项为0，获取气动/结构多学科耦合伴随方程为

(17)

即

(18)

3.2 延迟耦合伴随方程

(19)

式(18)被称之为延迟耦合伴随方程，可以看出，通过延迟伴随变量的引入，式(19)已经解耦，各个学科之间的影响通过方程右端的强迫项来实现，不同学科方程之间可以进行松耦合迭代，大幅度降低了方程求解难度。

其中，流场伴随方程强迫项为

(20)

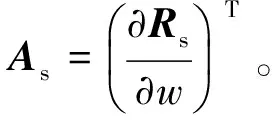
(21)

式中:wρ、wρ u、wρ v、wρ E和wρ w对应守恒变量的展开表达式。

由结构静力学方程(结构节点个数为Ns),有

(22)

上述矩阵维度取决于结构节点的维度以及CFD格心单元的维度，ψs的维度取决于有限元模型的网格类型，对于板壳单元，ψs为6Ns×1维度的矢量，∂Rs/∂w的转置矩阵As为5Na×6Ns矩阵。因此,结构残差对流场变量的导数∂Rs/∂w通过有限差分求出，解析表达式推导方式依赖于所采用的流固耦合方法。基于本文的虚功原理流固耦合方式，下面给出具体的推导。

由于FSC3D代码采用虚功原理实现气动力向结构载荷插值[18]，x方向(其他方向表达形式完全一致)结构载荷与气动力插值可以表达为矩阵与向量形式,即

(23)

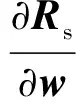
(24)

式(24)直接对守恒变量求导比较困难，可以变换为

(25)

代入耦合伴随方程，可以获得流场伴随方程强迫项最终表达形式。

同理，结构伴随方程强迫项为

(26)

上述矩阵维度同样取决于结构节点的维度以及CFD格心单元的维度，ψa为5Na×1维度的矢量，∂Ra/∂d的转置矩阵Aa为6Ns×5Na矩阵。流场残差对结构位移的导数∂Ra/∂d求解方式同样依赖于流固耦合方法以及变形网格方法，本文采用RBF_TFI变形网格方法，即

(27)

式中：X、Xsurf分别为空间网格与物面网格。从式(27)右端项中可以看出，流场残差对结构位移的导数∂Ra/∂d的解析表达形式依赖于所采用的动网格方法以及流固耦合技术，即第1项可以利用自动微分进行求导，对于弹簧法、径向基类型的动网格来讲，第2项可以推导出变形网格矩阵KD，第3项取决于结构位移向气动表面网格的插值方式，由于文中采用了RBF插值技术，很容易手工推导出位移向表面网格的变换矩阵KR。需要指出的是，为提高结构化变形网格的运算效率，文中采用了RBF_TFI混合算法，此时很难显式地推导出矩阵KD，该项的求导在文中由简单的单侧有限差分代替，由于RBF_TFI混合算法具有极高的效率，差分计算量可以忽略。

延迟伴随方程第1项强迫项为大型矩阵与矢量相乘，将其具体表达式展开，下标表达式为

结构伴随方程强迫项的下标表达式为

(28)

综合强迫项的整理，可以推导出耦合延迟伴随方程伪时间-残差表达形式为

(29)

式(29)流场伴随方程与结构伴随方程一步可以利用式(11)中的LU-SGS隐式迭代或雅克比迭代方法进行求解。

观察式(29)结构伴随方程，其本质上是大型稀疏矩阵求解，对于该类矩阵求解，常用的LU分解以及高斯消去法带来代价较大、在针对较多自由度结构有限元大型矩阵求解计算效率偏低等问题。综合考虑计算效率与存储量，Cholesky 分解算法是一个较为合理的选择，Cholesky 分解算法中主要包含LLT以及LDLT方法[18]，前者要求矩阵必须正定，而后者没有要求，鲁棒性更强，相对于迭代方法以及传统求逆方法，LDLT的计算效率较高，无需迭代且求解结果更为精确，因此本文采用并行LDLT方法代替迭代方法进行结构伴随方程求解，对结构伴随方程矩阵项进行LDLT分解，即

分解出Lij和dii元素后，结构伴随方程求解可以通过三步扫描快速完成，即

(30)

式中：ϑ和φ均为中间变量。

综合以上求解过程，可以看出延迟伴随方程的解耦求解方式，能够充分利用原有的求解体系，并不破坏原有程序的基本框架，由此可以直观地获取LCA系统各个分析模块的组装关系与工作流程，如图2所示。

对于延迟方程组式(19)中结构伴随方程的右端项，其含义是计算目标函数对结构位移的直接导数以及流场残差对结构位移导数与流场延迟伴随变量的乘积，观察单一流场学科目标函数导数的计算公式：

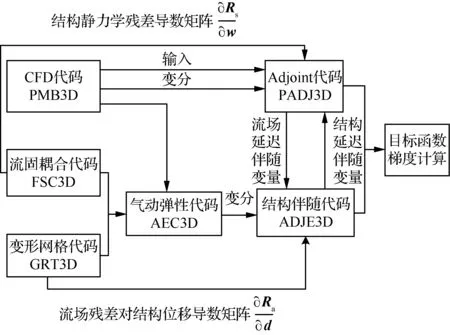
图2 LCA方法中各个学科分析模块组装与流程Fig. 2 Disciplines assembly and work flow of LCA method

(31)

不难发现,两者在表达形式上完全一致，仅仅在自变量扰动上不同，前者是结构位移，后者是参数化控制顶点，因此，结构伴随方程右端项计算与导数计算可以由同一模块来完成，只需将子程序的实参由参数化控制顶点P_ffd替换为结构位移CSD_displacement即可，如图3和图4所示。

图3 流场单学科目标函数导数计算模块Fig.3 Objective function derivative module of flow field single discipline

图4 结构伴随方程右端项计算模块Fig.4 Computational module for right end item of structural adjoint equation

进一步利用链式求导展开，即

(32)

可以看出，∂X/∂Xsurf的推导方式取决于所采用的变形网格方法，∂Xsurf/∂d的推导方式取决于所采用的流固耦合方法。

3.3 延迟耦合伴随方程求解与梯度计算

对式(18)加入伪时间项进行迭代求解，流场延迟伴随方程求解采用LU-SGS时间推进，结构延迟伴随方程求解采用LDLT方法进行求解，间隔指定的子迭代步数进行一次延迟伴随变量传递以及不同学科残差导数矩阵运算，实现强迫项的交换。

流场伴随方程求解采用单元数衡量的负载平衡，对等式计算以及MPI消息传递模式，本文求解器采用了多块对接网格技术，所以MPI传递的信息是各个进程分割面上的两层虚网格上的伴随变量。求解过程中流场延迟伴随方程的边界条件仍然采用矩阵形式[16]，结构伴随方程的相关导数矩阵由流固耦合程序FSC3D变分计算。求出延迟伴随变量ψ=[ψaψs]T，代入导数求解公式，可以获取目标函数的梯度为

(33)

式(33)的矩阵表达形式为

对各项进行进一步展开，有

式中：Swall、G分别代表物面网格以及空间网格。不难看出∂G/∂Swall的表达形式取决于所采用的变形网格方法，∂Swall/∂X的推导方式取决于所采用的参数化建模方法。

4 学科分析耦合系统的验证

采用HIRENASD(HIgh REynolds Number Aero-Structural Dynamics)模型[20]进行静气动弹性计算，并与试验数据进行对比，验证耦合分析手段的正确性。

图5给出了网格分布以及典型计算状态(Ma=0.8，Re=7.0×106)的弹性变形示意图；图6给出了刚性与气动弹性变形的机翼展向66%、95%站位压力分布与风洞试验的对比，其中,Cp为压力系数,x/c为展弦比。可以看出弹性变形数值模拟结果与试验数据更为吻合，验证了气动弹性手段的可靠性，可以为多学科耦合伴随系统数值模拟提供准确的多物理场信息。

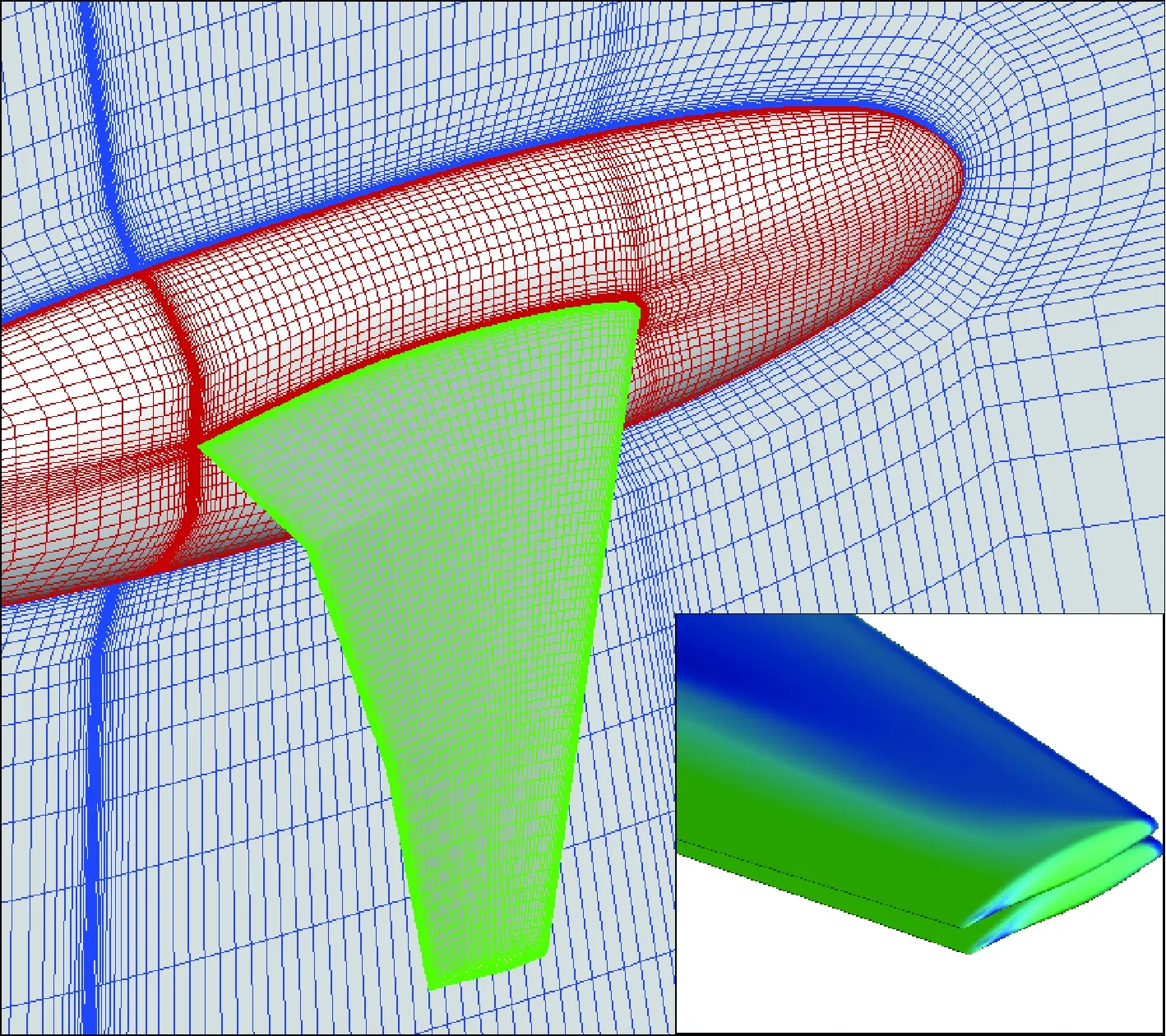
图5 CFD网格分布与弹性变形Fig.5 CFD grid distribution and aeroelastic deformation

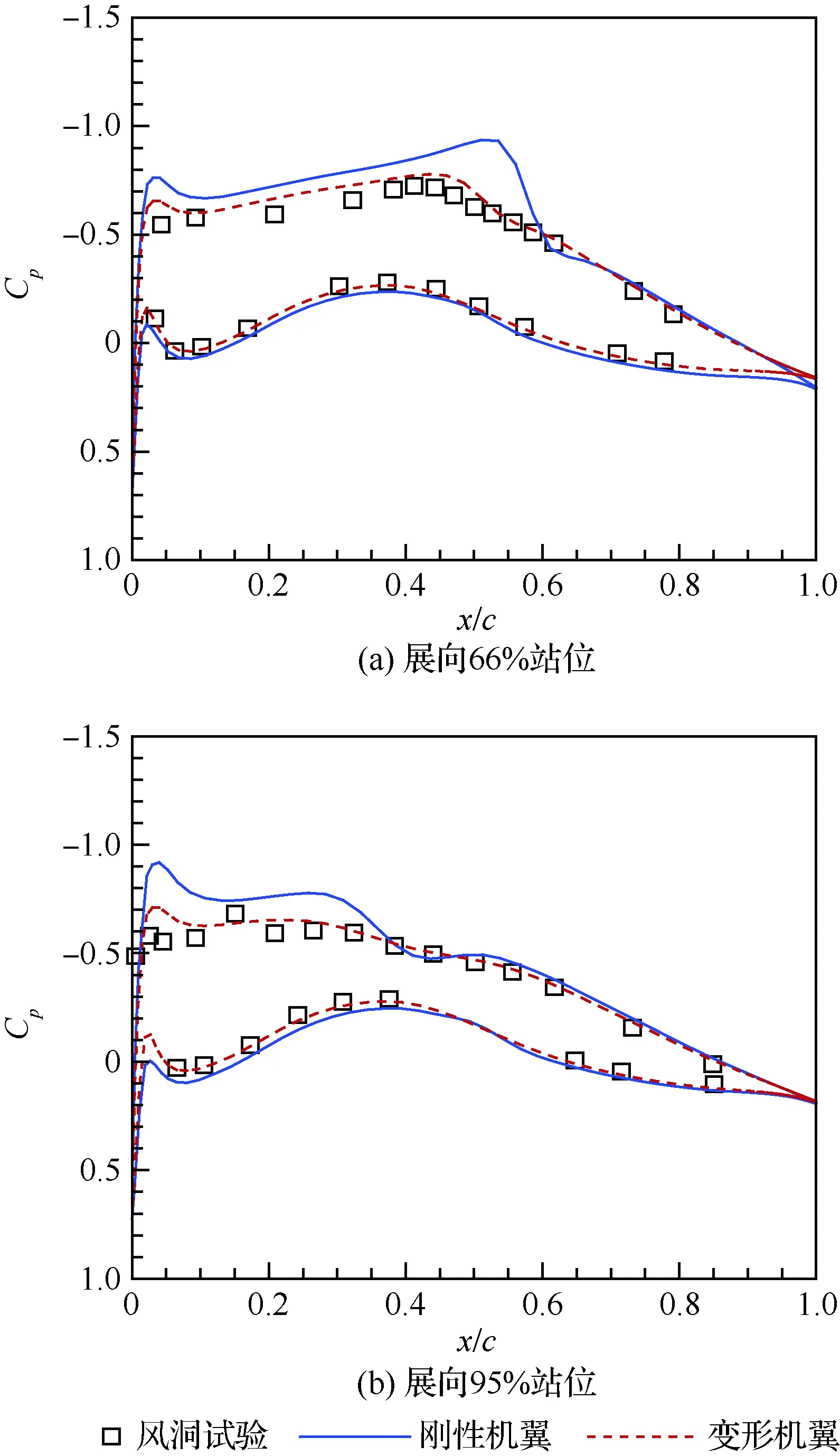
图6 压力分布与风洞试验对比Fig.6 Pressure distribution compared with wind tunnel test

5 典型工程算例测试

基于CRM (Common Research Model)标准算例构型，进行本文的方法梯度计算精度以及收敛特性验证。

主要部件包含机翼、机身、平尾以及立尾。网格划分为290块，半模网格规模为1 260万，如图7所示。采用中心格式、SST湍流模型、LU-SGS时间推进以及多重网格加速收敛技术，64核并行计算。

图8给出了基于非均匀有理B样条(NURBS)基函数的自由式变形 (FFD)参数化示意图，共采用200个控制顶点实现机翼气动外形参数化建模；为方便耦合系统的测试，结构有限元建模采用简化板壳单元，主要结构单元包含梁、翼肋等，结构参数化方法采用FFD技术，实现梁、翼肋的高度和宽度变化，有限元模型节点数为490个，如图9和图10所示。图11给出了流固耦合与流场求解模块共用一个模块的残差以及固定升力系数下气动力的收敛历程，每500步进行一次流固耦合模块调用，每10步进行一次迎角调整，经过8次气动弹性静力学方程求解，5 000步左右的迭代，气动力基本趋于收敛，与单一流场计算相比，计算量增加很小。

图12给出了典型耦合步的弹性变形及其局部视图。图13给出了多学科耦合伴随系统残差收敛历程，可以看出耦合系统的残差收敛稳定，且耦合产生的跳跃残差也随着迭代过程下降，这说明随着迭代的收敛，多学科延迟耦合的解与原始耦合伴随系统趋于一致；图14给出了结构伴随变量残差随迭代步数的收敛历程，可以看出经过6次的强迫项耦合计算，结构伴随方程的解基本收敛。进一步对耦合伴随梯度的计算精度与差分方法进行对比，差分步长为0.000 1。

图7 CFD表面网格分布Fig.7 CFD gird distribution on wall

图8 自由式变形参数化Fig.8 Free-form deformation lattice for parameterization

图9 蒙皮结构有限元网格Fig.9 Finite element grid of skin structure

图10 梁、肋等有限元网格Fig.10 Finite element grid of beam and rib

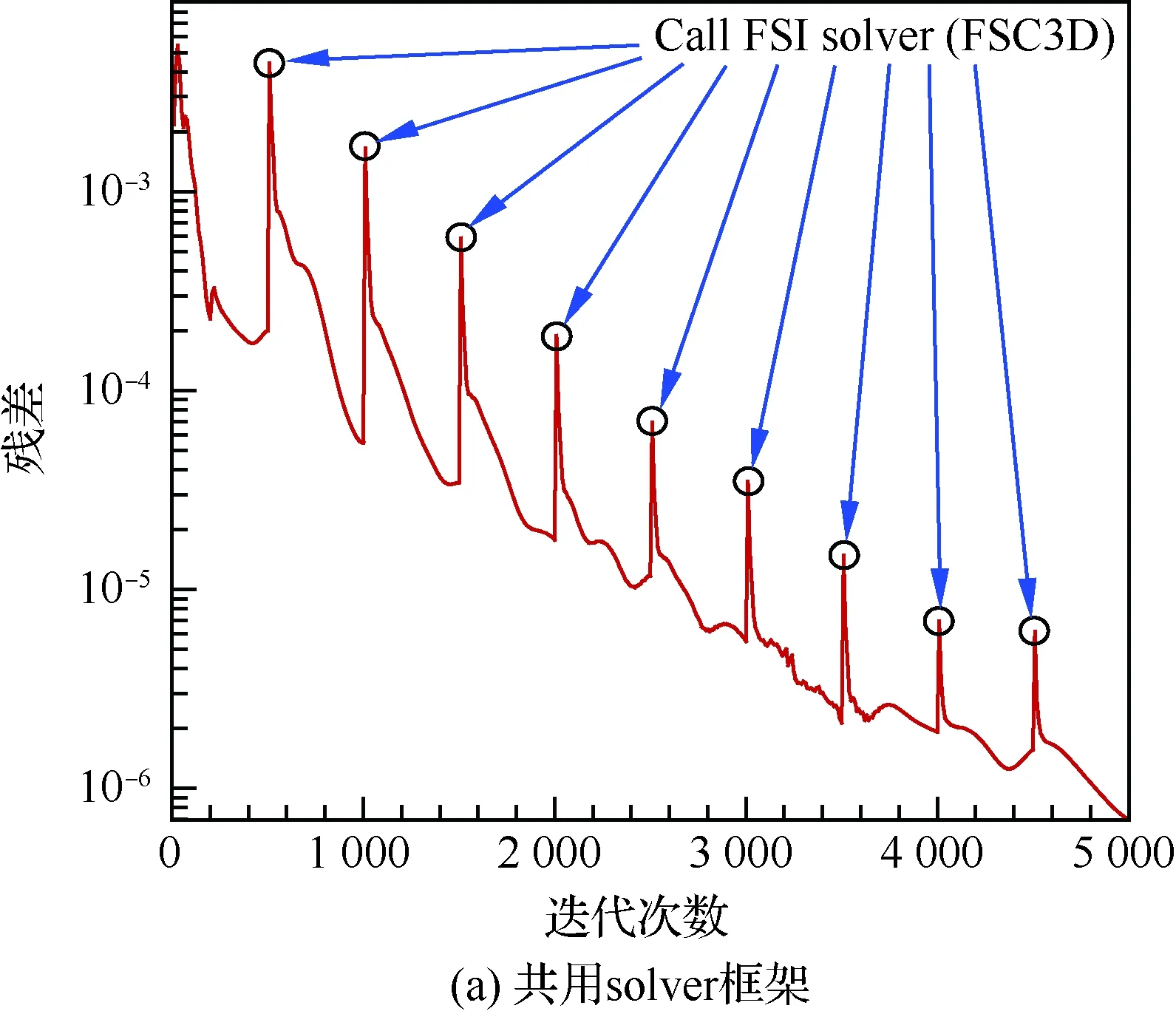
图11 气动弹性收敛历程Fig.11 Process of aeroelastic convergence

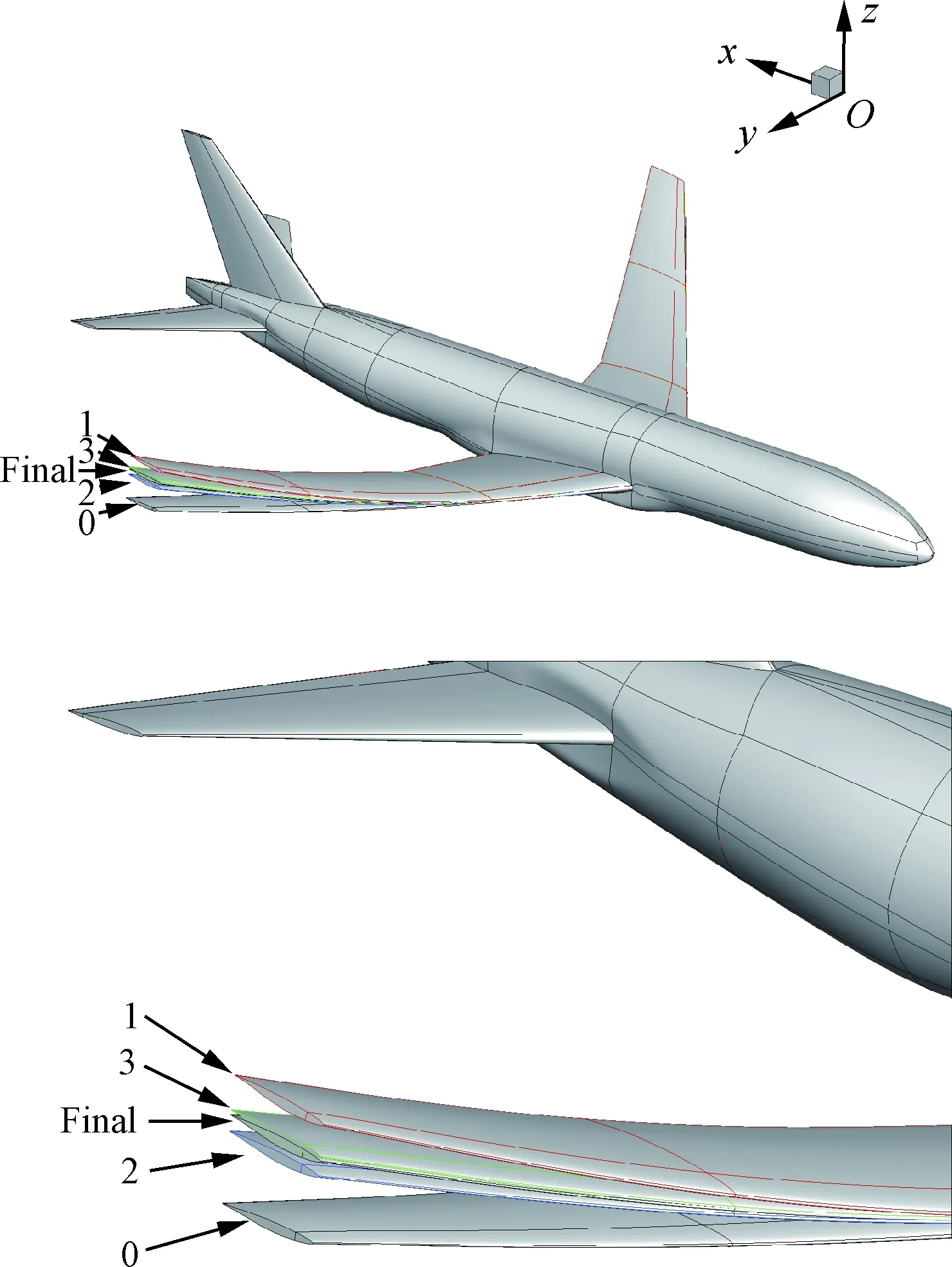
图12 典型耦合步长弹性变形及局部视图Fig.12 Elastic deformation with typical coupling step and local view of elastic deformation

图13 耦合伴随系统残差收敛历程Fig.13 Process of residual convergence of coupled adjoint system

求解气动力对结构有限元厚度等设计变量的导数时，对结构刚度矩阵的影响进行了充分考虑。由于气动弹性系统差分计算量极为庞大，因此本文给出了阻力系数对典型的设计变量(结构有限元设计变量主要对蒙皮与梁厚度)梯度与差分的对比，如图15所示，横坐标代表设计变量的编号，纵坐标代表目标函数对设计变量的梯度，耦合伴随系统计算的梯度与差分(FD)幅值、趋势基本一致，满足多学科综合设计要求,δ为扰动量。本文完成了气动力对外形设计变量以及结构有限元设计变量两类导数的验证。结构应力(最常关注的是冯·米塞斯应力)对外形设计变量、结构设计变量的两类导数，将在实现求解系统与有限元分析程序模块紧耦合后进行校核，此时耦合伴随系统右端项将更换为结构应力对多物理场状态变量的变分形式，这是本文进一步的研究工作。

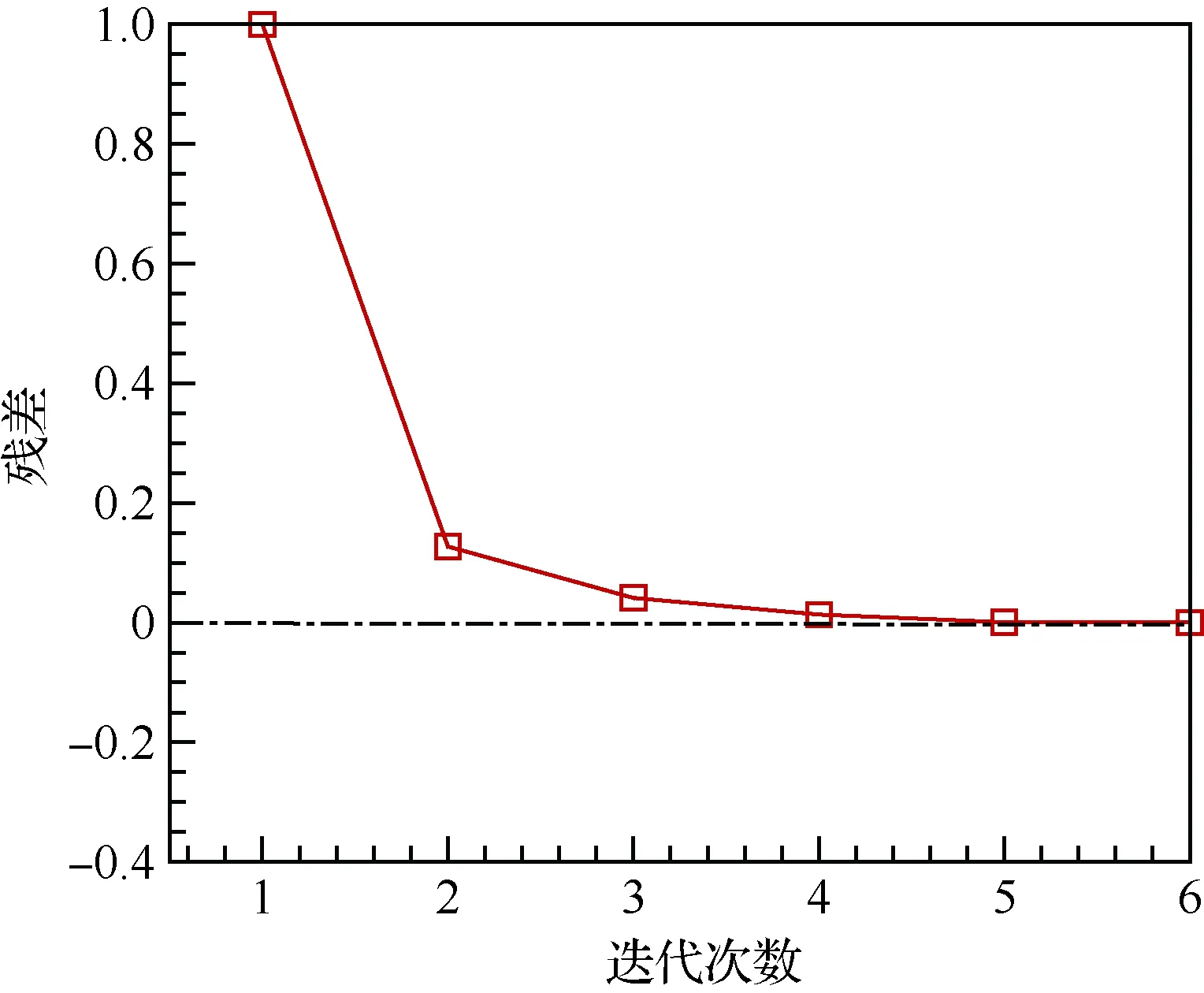
图14 结构伴随系统残差收敛历程Fig.14 Process of residual convergence of structural adjoint system

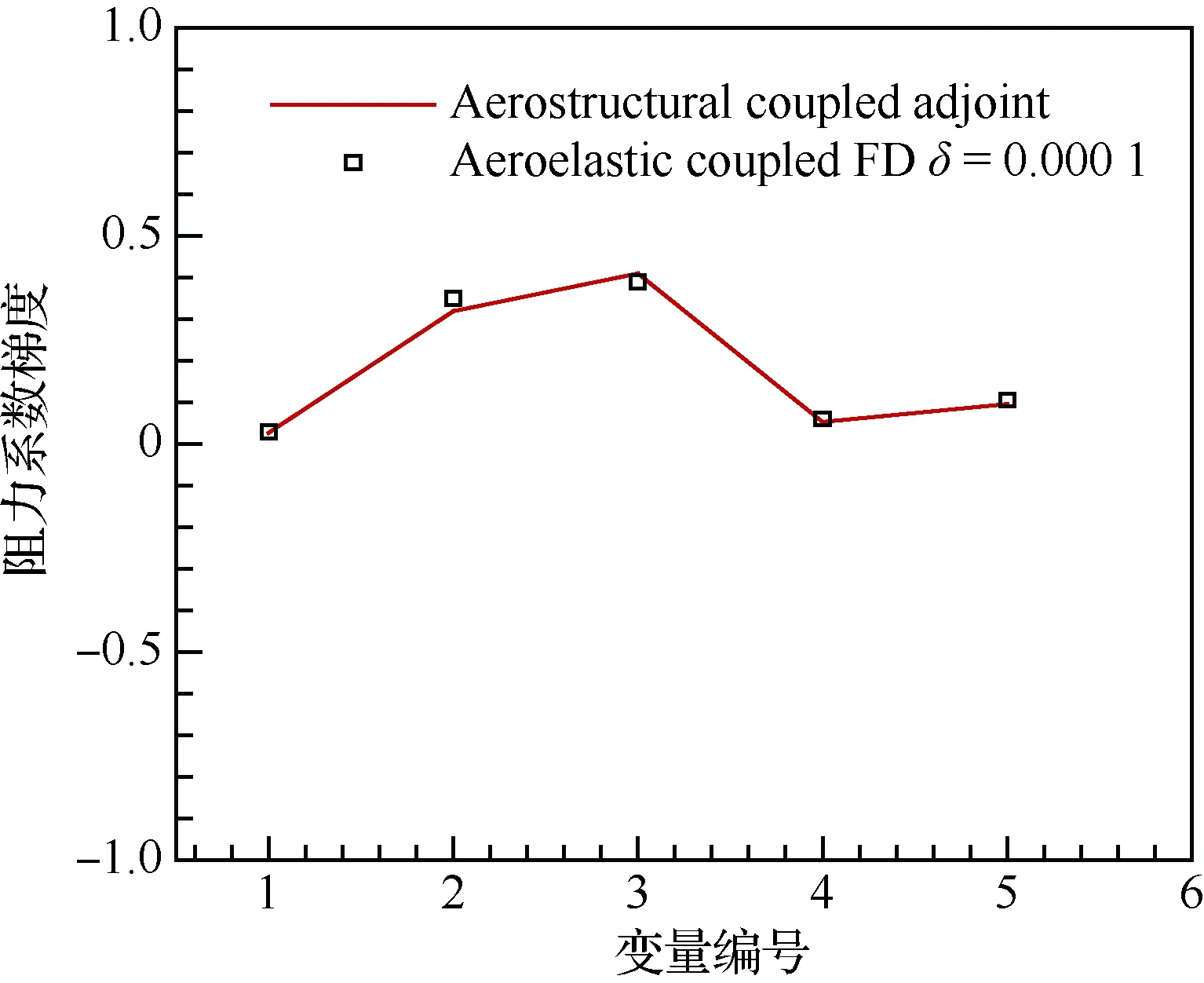
图15 阻力系数对外形/结构设计变量的梯度对比Fig.15 Gradient of drag coefficients vs configuration/structural design variables

6 结 论

基于自主研发的大规模并行化结构网格RANS求解器PMB3D以及流固耦合模块，开展了多学科耦合伴随方程构造、求解方法的研究。

1) 基于流固耦合与流场求解共用模块的不完全收敛解进行静气动弹性求解，具有较高的计算效率，相对于单次流场计算，计算量增加很少。

2) 耦合伴随方程的第1项非对角线项可以通过流固耦合方式推导出其解析表达式。所采用的变形网格、参数化以及流固耦合方法在耦合伴随系统推导中，决定了耦合系统本身的运算效率以及各项的具体表达形式。基于所采用的具体算法，本文给出了具体的推导结果，结合对原始变量变分以及链式求导，推导了虚功原理载荷传递方式下，流场伴随方程交叉导数项的解析表达式；对变形网格混合算法求导问题采用有限差分近似简化处理方式，降低了推导难度。

3) 结构伴随方程的强迫项与梯度计算公式在表达形式上完全一致，仅在自变量扰动上不同，前者是结构位移，后者是设计变量，因此，文中结构伴随方程强迫项计算与导数计算采用同一模块来完成。文中进一步采用LDLT并行分解方法代替传统迭代方法，实现结构伴随方程的高效方便求解，结构伴随变量解趋于收敛仅需较少的耦合次数。

4) 延迟耦合伴随系统能够大大降低求解体系对内存的需求，同时也有利于程序的简捷化、模块化。

5) 文中采用的求解方法以及简化处理方式所构建的离散伴随系统效率较高，收敛稳定性好，耦合系统的梯度求解精度满足综合设计需求。

本文的研究工作完成了气动力对外形设计变量、结构有限元设计变量两类导数的验证，为进一步的多学科敏感性分析提供了研究基础。下一步的研究内容为在实现求解系统与有限元分析程序模块紧耦合后，求解结构应力对外形设计变量、结构设计变量的两类导数。

致 谢

在本文的研究工作中，大连理工大学陈飙松教授、张盛副教授等在结构有限元建模、有限元分析等方面给予了有益的建议，空气动力学国家重点实验室孙岩助理研究员提供了标模计算网格，在此表示感谢！

参 考 文 献

[1] MARTINS J R R A. A coupled-adjoint method for high-fidelity. Aero-structural optimization[M]. Stanford: Stanford University Press, 2002.

[2] MADER C A, KENWAY G K W, MARTINS J R R A. Towards high-fidelity aerostructural optimization using a coupled adjoint approach[C]∥12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Reston, VA: AIAA, 2008.

[3] KENWAY G K W, MARTINS J R R A. Multipoint high-fidelity aerostructural optimization of a transport aircraft configuration[J]. Journal of Aircraft, 2014, 51(1): 144-160.

[4] LEOVIRIYAKIT K, JAMESON A. Case studies in aero-structural wing planform and section optimization: AIAA-2004-5372[R]. Reston, VA: AIAA, 2004.

[5] ABU-ZURAYK M, BREZILLON J. Shape optimization using the aero-structural coupled adjoint approach for viscous flows[C]∥Evolutionary and Deterministic Methods For Design, Optimization and Control, 2011.

[6] MARCELET M, PETER J, CARRIER G. Sensitivity analysis of a strongly coupled aero-structural system using direct and adjoint methods: AIAA-2008-5863[R]. Reston, VA: AIAA, 2008.

[7] GHAZLANE I, CARRIER G, DUMONT A. Aerostructural adjoint method for flexible wing optimization: AIAA-2012-1924[R]. Reston, VA: AIAA, 2012.

[8] 左英桃， 高正红， 詹浩.基于N-S方程和离散共轭方法的气动设计方法研究[J].空气动力学学报, 2009, 27(1):67-72.

ZUO Y T, GAO Z H, ZHAN H. Aerodynamic design method based on N-S equations and discrete adjoint approach[J]. Acta Aerodynamica Sinica, 2009, 27(1): 67-72 (in Chinese).

[9] 熊俊涛， 乔志德， 杨旭东， 等. 基于黏性伴随方法的跨声速机翼气动优化设计[J]. 航空学报, 2007, 28(2): 281-285.

XIONG J T, QIAO Z D, YANG X D, et al. Optimum aerodynamic design of transonic wing based on viscous adjoint method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 281-285 (in Chinese).

[10] 屈崑， 李记超， 蔡晋生. CFD数学模型的线性化方法及其应用[J]. 航空学报， 2015, 36(10): 3218-3227.

QU K, LI J C, CAI J S. Method of linearizing computational fluid dynamics model and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3218-3227 (in Chinese).

[11] 张朝磊， 厉海涛， 丰镇平. 基于离散伴随方法的透平叶栅气动优化[J]. 工程热物理学报, 2012, 33(4): 47-50.

ZHANG C L, LI H T, FENG Z P. Aerodynamic opti-mization design of turbomachinery cascade based on discrete adjoint method[J]. Journal of Engineering Thermophysics, 2012, 33(4): 47-50 (in Chinese).

[12] 高宜胜， 伍贻兆， 夏健. 基于非结构网格离散型伴随方法的翼型优化[J]. 空气动力学学报, 2013, 31(2): 244-249.

GAO Y S, WU Y Z, XIA J. A discrete adjoint-based approach for airfoil optimization on unstructured meshes[J]. Acta Aerodynamica Sinica, 2013, 31(2): 244-249 (in Chinese).

[13] 李彬， 邓有奇， 唐静， 等. 基于三维非结构混合网格的离散伴随优化方法[J]. 航空学报， 2014, 35(3): 674-686.

LI B, DENG Y Q, TANG J, et al. Discrete adjoint optimization method for 3D unstructured grid[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 674-686 (in Chinese).

[14] 张科施， 韩忠华， 李为吉， 等. 一种考虑气动弹性的运输机机翼多学科优化方法[J]. 空气动力学学报, 2008, 26(1): 1-7.

ZHANG K S, HAN Z H, LI W J, et al. A method of coupled aerodynamic/structural integration optimization for transport-wing design[J]. Acta Aerodynamica Sinica, 2008, 26(1): 1-7 (in Chinese).

[15] 刘刚, 肖中云, 王建涛, 等. 考虑约束的机载导弹导轨发射数值模拟[J]. 空气动力学学报， 2015, 33(2): 192-197.

LIU G, XIAO Z Y, WANG J T, et al. Numerical simulation of missile air-launching process under rail slideway constraints[J]. Acta Aerodynamica Sinica, 2015, 33(2): 192-197 (in Chinese).

[16] 黄江涛， 刘刚， 周铸, 等. 基于离散伴随方程求解梯度信息的若干问题研究[J]. 空气动力学学报， 2017, 35(4): 554-562.

HUANG J T, LIU G, ZHOU Z, et al. Investigation of gradient computation based on discrete adjoint method[J]. Acta Aerodynamica Sinica, 2017, 35(4): 554-562 (in Chinese).

[17] ALLEN C B, RENDALL T C S. Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions: AIAA-2007-3804[R]. Reston, VA: AIAA, 2007.

[18] 覃华， 徐燕子. 用LDLT并行分解优化大规模SVM的训练效率[J]. 计算机工程与应用, 2011, 47(12): 200-212.

QIN H， XU Y Z. Improving SVM’s learning efficiency by using matrix LDLT parallel decomposition[J]. Computer Engineering and Applications, 2011, 47(12): 200-212 (in Chinese).

[19] SPEKREIJSE S P, BOERSTOEL J W. An algorithm to check the topological validity of multi-block domain decompositions[C]∥Proceedings 6th International Conference on Numerical Grid Generation in Computational Field Simulations, 1998.

[20] BALLMANN J, BOUCKE A, CHEN B, et al. Aero-structural wind tunnel experiments with elastic wing models at high reynolds numbers (HIRENASD-ASDMAD): AIAA-2011-0882[R]. Reston, VA: AIAA, 2011.