AZ31镁合金板热成形中的屈服和损伤: 本构实现与数值分析

周霞，文冬，沈梦祺, 宋尚雨

1.大连理工大学 工业装备结构分析国家重点实验室, 大连 116024 2.大连理工大学 工程力学系, 大连 116024 3.国际计算力学 研究中心, 大连 116024

作为一种轻质结构材料，镁合金由于高的比强度、比刚度以及优异的减振性能在航空航天、汽车、电子等领域具有很好的应用潜力[1]。然而，由于镁合金具有密排六方晶格结构，其室温塑性差，难以塑性加工，因而其塑性加工产品的开发应用还远不如钢铁、铝、铜成熟[2]。此外，镁合金力学性能还具有明显的各向异性及拉压不对称性，塑性加工成形屈服本构模型中材料参数不是定值，而是随着塑性流动而变化[3]，即屈服面形状随塑性流动而变化；随着温度升高，虽然镁合金塑性成形能力增强[4]，但变形温度、变形速率及应力状态对其塑性变形能力也有重要影响。镁合金板材的温热冲压成形过程是一个复杂的多参数热力耦合非线性过程，也是镁合金板材加工成形的研究热点，基于合适材料模型的镁合金板材温热成形数值模拟可以准确预测板料成形性能和塑性行为及破坏方式。同时，由于镁合金材料的成形性较差，需要从微观角度研究其损伤的发展。因此对镁合金板料冲压成形各向异性屈服本构和损伤模型的研究具有重要意义[5]。

在过去的几十年中，已有相关学者提出了许多金属板料塑性成形各向异性屈服准则。其中Hill48各向异性模型[6]由于只包含6个各向异性参数，对于一些复杂结构金属材料并不能准确描述。随后Barlat等相继提出了Yld91各向异性屈服函数[7]、 考虑了不同方向屈服应力和塑性应变比r值变化的Yld96屈服函数[8]以及对Yld96改进的Yld2000-2d屈服函数[9]。对于密排六方(Hexagonal Close Packed, HCP)晶格结构材料，由于存在拉压不对称性，上述模型并不一定准确适用于这种结构材料的成形。针对该问题，Hosford[10]通过对Hill各向异性屈服准则进行修正来描述材料各向异性屈服响应和拉压不对称性。但在该模型中由于各向异性和拉压不对称的耦合不能系统地确定各个材料参数。在此基础上，Cazacu等和Plunkett等分别提出的CPB04本构模型[11]和改进的CPB06本构模型[12]，能够描述镁合金等HCP晶格材料的各向异性和拉压不对称性，且改进的CPB06本构模型由于通过多次线性变换引入更多的各向异性参数因而具有较高的精度。近年来，Tari和Worswick[13]考虑到AZ31镁合金在塑性成形畸变硬化过程中，屈服面形状随着塑性变形而发生变化，提出了考虑参数演化的AZ31镁合金各向异性屈服CPB06ex3ev本构模型，该模型虽能较准确地描述板材料的拉压不对称各向异性屈服及其屈服面形状的演化，但在板成形模拟中还需要考虑准确的损伤破坏模型[14]。目前对金属板材成形过程损伤行为的研究多基于连续介质损伤方法的定性预测，而基于细观损伤力学及成形极限理论对板料成形性分析的研究日趋广泛[15-16]，但针对镁合金在温热成形过程中的各向异性屈服和细观损伤演化耦合的研究还未见报道。

本文选用适用于HCP晶格结构，能同时反映各向异性和拉压不对称屈服的CPB06各向异性屈服准则来描述镁合金的各向异性屈服，镁合金的损伤准则采用适用于延性金属的Gurson-Tvergaard-Needleman(GTN)损伤准则[17-18]。考虑到镁合金的屈服面随着塑性变形而变化，对CPB06各向异性屈服本构进行了修正，并结合GTN损伤模型，得到了考虑损伤演化和屈服面形状变化的CPB06-GTN损伤本构模型，编译得到了相应的VUMAT本构子程序，并嵌入到ABAQUS/Explicit中，采用单个单元对本构模型进行了验证，然后将本构子程序应用到冲压成形模拟中，预测了镁合金的热成形，模拟预测与实验结果吻合较好。

1 本构模型

1.1 CPB06各向异性拉压不对称屈服本构

在平面应力条件下，CPB06本构模型的具体函数形式为[19]

(1)

式中：k为用于描述材料拉压非对称性的参数(-1≤k≤1)；a为与材料有关的参数，在使用时a的取值需要不断调整，对于AZ31镁合金可取2；Σi(i=1, 2, 3)为对应力偏张量线性变换并求主值的结果，可用式(2)和式(3)进行求解：

(2)

(3)

其中：式(2)中矩阵C为描述各向异性屈服的线性变换张量；S为Cauchy应力偏张量；式(3)中σ11、σ22、σ12为Cauchy应力偏张量对应的应力分量；式(1)中Σ1、Σ2、Σ3是Σ的主值，且

从以上结果推导可得出，当k=0，C为4阶单位矩阵，且a=2时，该模型与Mises屈服准则等效。

1.2 GTN损伤本构

用来描述由于孔洞不断长大、形核、聚合导致的宏观材料软化及破裂现象的GTN损伤模型[17-18]可表示为

(1+q3f*2)=0

(4)

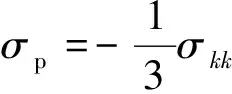
材料进入塑性时由流动法则可计算得到塑性应变增量为

(5)

式中：dλ为一个正标量因子；Ψ=Ψ(σp,σe,Hα)为流动势，对于相关流动法则φ和Ψ是一致的，Hα(α=1,2)为状态变量σij为应力分量。在各向异性屈服GTN损伤模型式(5)中流动法则可表示为

(6)

式中：I为4阶单位矩阵；n为流动方向；对于各向异性材料，流动方向表示为

(7)

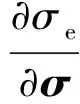
式(6)中总的塑性应变增量可看做由两部分组成：

(8)

(9)

式中：Δεp为宏观塑性应变张量与静水应力对应的塑性体积应变部分；Δεq为宏观塑性应变张量与等效应力对应的等效塑性应变部分。

由式(9)消去Δλ可得到

(10)

由等效塑性功原理，可以得到基体材料等效塑性应变的演化方程：

(11)

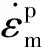
(12)

材料的损伤演化包含原有孔洞的长大和新孔洞的形核：

(13)

(14)

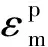
在最终阶段，考虑到孔洞的聚合和材料的失效，Needleman和Tvergaard[18]通过引入等效体积分数函数f*(f)对原有模型进行了修正：

(15)

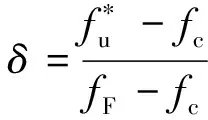
1.3 修正的CPB06-GTN本构模型

本节基于多孔材料的CPB06-GTN宏观各向异性屈服准则[20]，并对其进行了修正，使其适用于壳单元，损伤演化部分不变，具体形式为

(1+q3f*2)=0

(16)

式中：σq为CPB06屈服模型的等效应力；q1、q2、q3、σp、σm、f*以及损伤参数的演化均与GTN损伤模型相同。

σq=m·

(17)

式中：

m=

式(16)中：

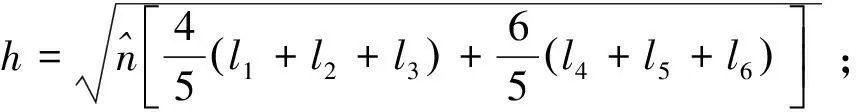
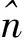
(18)

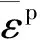
(19)

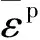
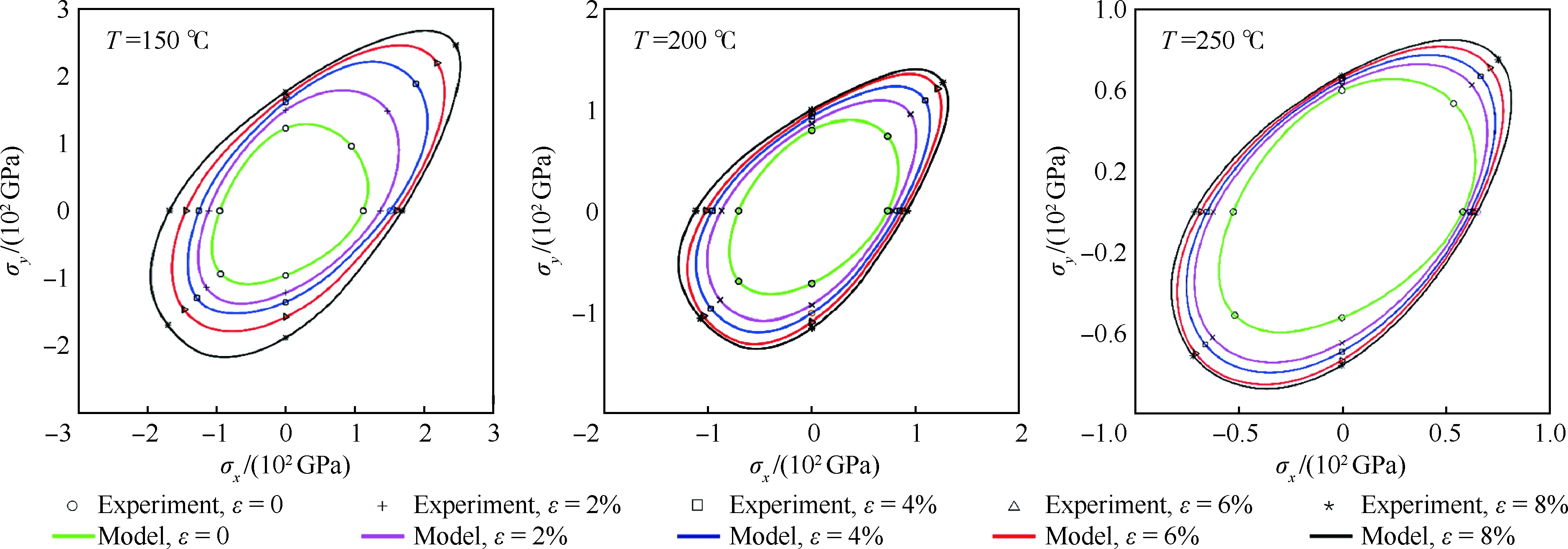
图1 应变率为和不同温度(T=150, 200, 250 ℃)时基于CPB06模型拟合得到的屈服面形状演化Fig.1 Evolution of yield surface with accumulated plastic strain obtained by anisotropic CPB06 model at strain rate of 0.001 s-1 and different temperatures (T=150, 200, 250 ℃)

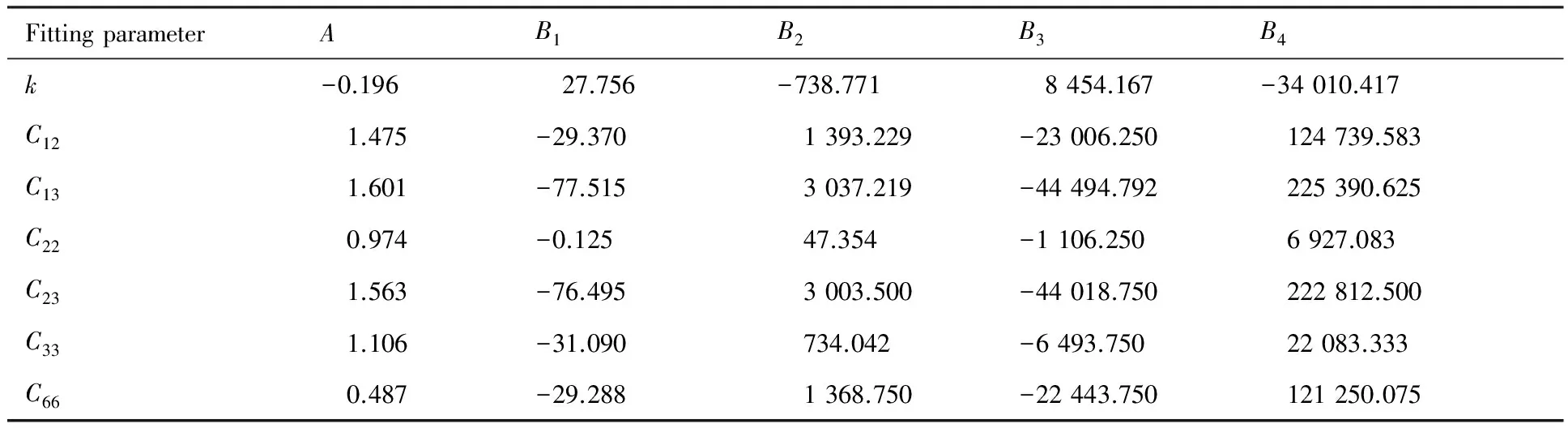
表1 150 ℃时各向异性CPB06屈服本构参数随等效塑性应变的变化Table 1 Variation of anisotropic CPB06 yield criterion parameters with effective plastic strain at 150 ℃

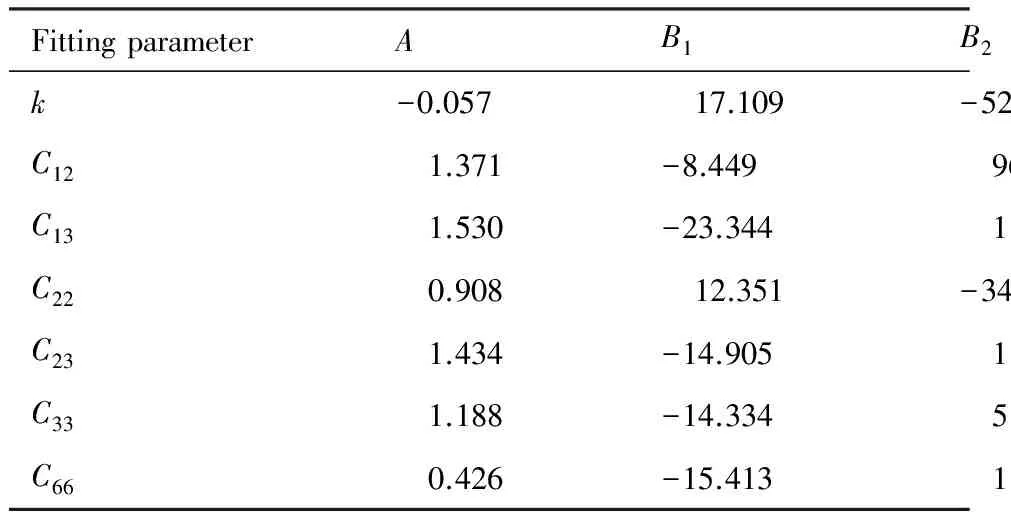
表2 200 ℃时各向异性CPB06屈服本构参数随等效塑性应变的变化Table 2 Variation of anisotropic CPB06 yield criterion parameters with effective plastic strain at 200 ℃

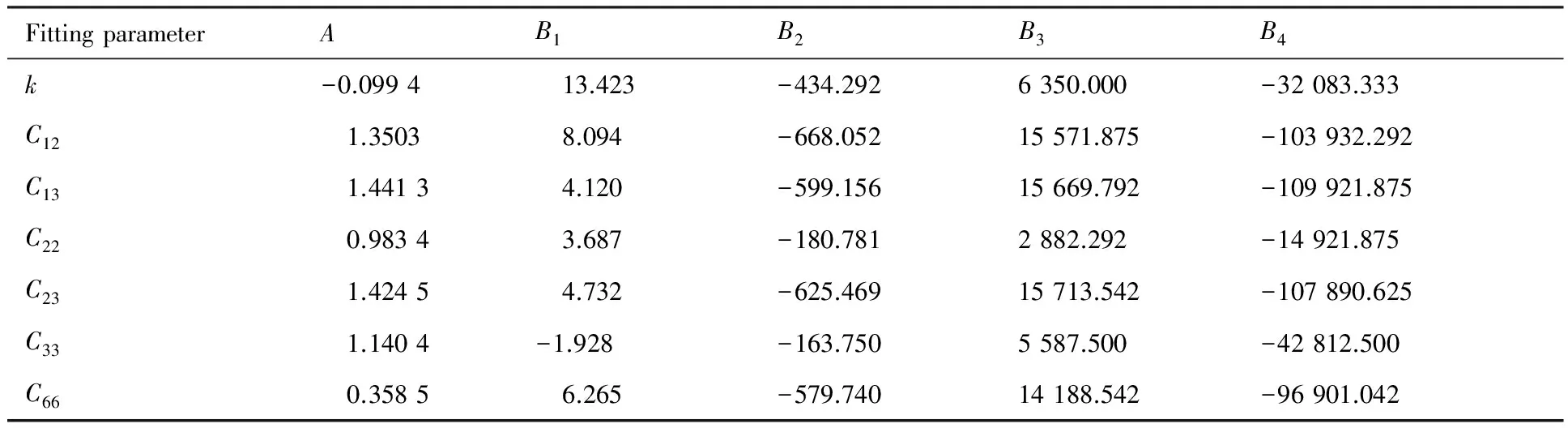
表3 250 ℃时CPB06各向异性屈服本构参数随等效塑性应变的变化Table 3 Variation of anisotropic CPB06 yield criterion parameters with effective plastic strain at 250 ℃

镁合金材料的各向同性硬化行为通过定义轧制方向材料的等效塑性应变与拉伸应力的关系来描述，并以轧制方向作为参考方向，沿轧制方向单向拉伸的屈服应力和塑性应变关系可用式(20)简化[13]，即Cowper-Symonds模型：

(20)

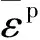
表4AZ31B镁合金在不同温度下的硬化参数

Table4HardeningparametersofAZ31Bmagnesiumalloyatdifferenttemperatures

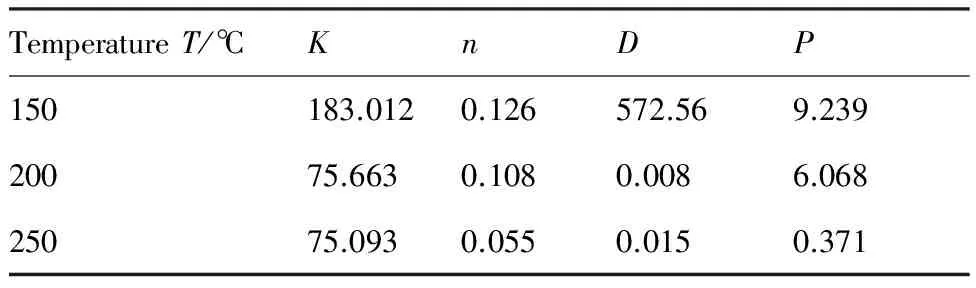
TemperatureT/℃KnDP150183．0120．126572．569．23920075．6630．1080．0086．06825075．0930．0550．0150．371

(21)

2 数值算法实现及验证

2.1 VUMA子程序实现

将改进后的塑性各向异性GTN损伤模型，借助用户材料子程序VUMAT嵌入到有限元软件ABAQUS的显式分析模块中，进行镁合金的冲压成形模拟，VUMAT子程序需要根据应变增量对应力进行更新，其中一个条件需要判断材料是否进入塑性状态，并求解出塑性应变；冲压成形中的镁合金板采用的是壳单元，不同于一般三维单元的是，壳单元VUMAT子程序除了需要完成应力更新外，还需要对厚度方向的应变进行更新；壳单元的各向异性屈服GTN损伤模型的VUMAT子程序算法分为弹性预测和塑性修正[23]，具体的应力更新计算过程如下：

步骤2假设应变增量为完全弹性，计算得到弹性预测应力：

(22)

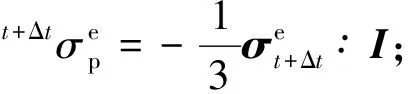
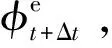
(23)

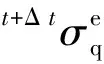
步骤4塑性修正，通过迭代求解塑性应变确定流动方向n：

(24)

求解以下非线性方程组，保证等式成立：

(25)

U、V分别对应式(10)和式(4)的方程，这里采用Newton-Raphson法迭代求解两个未知量k+1Δεp和k+1Δεq；设cp和cq分别为Δεp和Δεq的修正量，迭代式为

(26)

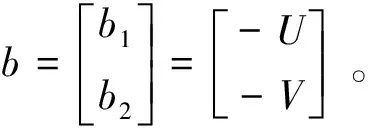
更新相应的等效应力σq和静水应力σp：

(27)

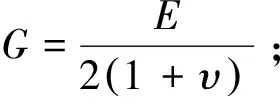
(28)

(29)

式中：左上标k和k+1 表示迭代次数；当孔洞体积率f>fc时，等效孔洞体积分数f*=fc+δ(f-fc)。

结合硬化准则对基体材料的屈服应力进行更新：

(30)

继续完成迭代，直到|U|和|V|<10-8时停止迭代，此时迭代收敛，式(25)成立，进入下一步。

步骤5完成应力更新，判断孔洞体积率是否达到临界值。

将由步骤4迭代求解得到的Δεp和Δεq代入式(8)可得到相应的塑性应变增量：

(31)

通过对预测应力进行修正即可得到当前状态的真实应力：

σ=σtr-Ce:Δεp

(32)

式中：σtr为弹性预测应力；Ce为4阶弹性模量；Δεp为塑性应变增量；当孔洞体积率达到临界值时，则相应的控制单元删除的状态变量等于0，意味着单元失效。

步骤6对壳单元厚度方向的应变增量作更新。

(33)

式中：dσ11和dσ22分别为x方向和y方向的应力增量。

(34)

式中：dεp是宏观塑性应变张量与静水应力对应的塑性体积增量部分；dεq是宏观塑性应变张量与等效应力对应的等效塑性应变增量部分；n11和n22分别为流动方向n在x和y方向的分量。

综上，可得出厚度方向的应变增量为

dεq(-n11-n22)

(35)

步骤7结束当前时间步，进入下一时间步。

具体程序流程图如图2所示。

图2 考虑本构参数演化的CPB06-GTN损伤模型VUMAT程序流程Fig.2 Flowchart of VUMAT subroutine for the coupled CPB06-GTN damage model considering yield loci evolution

2.2 单个单元测试

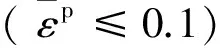
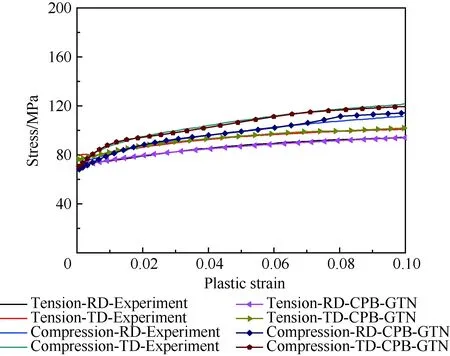
图3 采用(VUMAT)子程序模拟的单轴拉伸和压缩应力应变曲线及其与实验数据[13]的比较Fig.3 Uniaxial tensile and compressive stress-strain curves for a single unit obtained by subroutine VUMAT and their comparison with experimental data[13]

3 冲压成形算例分析

3.1 200 ℃等温成形模拟

本节基于VUMAT子程序对AZ31B镁合金板温热深拉成形进行了数值模拟，模拟使用的AZ31B镁合金板厚度为1.57 mm，直径为 228.6 mm；冲头外径为101.6 mm，冲头圆角半径为8.0 mm，凹模直径为106 mm，凹模圆角半径为8 mm，冲压成形时镁合金板由压边圈压紧，通过在压边圈上施加压边力防止起皱，由于模型具有对称性，为节省计算时间选取1/4模型进行分析。有限元模型如图4所示，其中镁合金采用S4R壳单元，厚度方向有5个积分点，其他模具均设置为离散刚体。由于实际成形时采取了润滑措施，模拟时的摩擦系数取0.04。

图5(a)显示了拉深比为2.25、压边力为80 kN时深拉杯的壁厚分布云图，STH表示深拉变形过程中深拉杯的厚度。由图可知，此时无法完成深拉成形，镁合金板深拉时其侧壁处发生开裂，镁合金深拉杯的破坏形态和位置与Tari等[24]实验结果吻合。图5(b)显示了该条件下不同极限应变点(点1, 2, 3)的模拟结果与Li等[25]实验测得的成形极限图(Forming Limit Diagram, FLD)的比较，可以进一步看出，在成形极限曲线FLD下方的极限应变点2和点3处于安全区域，而极限应变点1则处于临界破裂区，对应图5(a)的不同部位，有限元模拟结果与成形极限图结果吻合。这说明本文的各向异性GTN损伤模型能够准确预测镁合金温热深拉成形时的损伤失效。

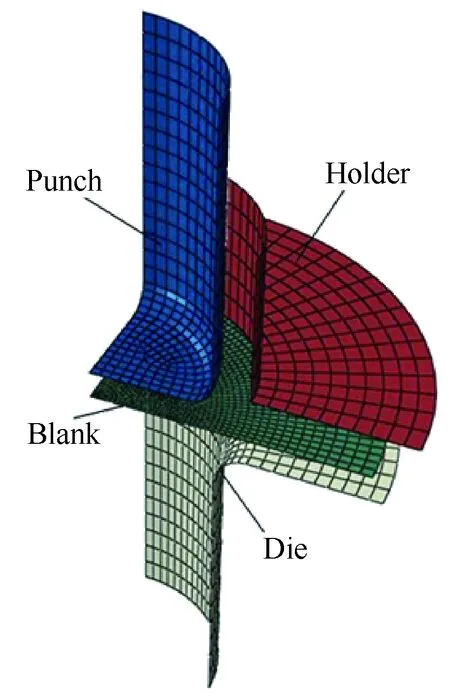
图4 深拉成形有限元网格模型Fig.4 Deep drawing finite element mesh model

当采用直径为203.2 mm的镁合金板，对应的拉深比为2.0，施加压边力为48 kN时，能够顺利完成深拉成形，成形后深拉杯的壁厚分布如图6(a)所示。从图6(a)可看出，成形后深拉杯的壁厚呈不均匀分布，杯壁区靠近冲头圆角半径附近壁厚发生较大的减薄，且轧制方向(X轴方向)侧壁上的厚度较薄，而横向(Z轴方向)侧壁的厚度与轧制方向侧壁厚度相比较厚，但由于高温下各向异性减弱，因而并没有出现明显的制耳。同样条件下模拟所得的冲头力-位移曲线与Tari等[24]的实验结果对比如图6(b)所示。上述成形条件下的对比结果也说明了本文的本构模型能较好地模拟镁合金的完整成形。

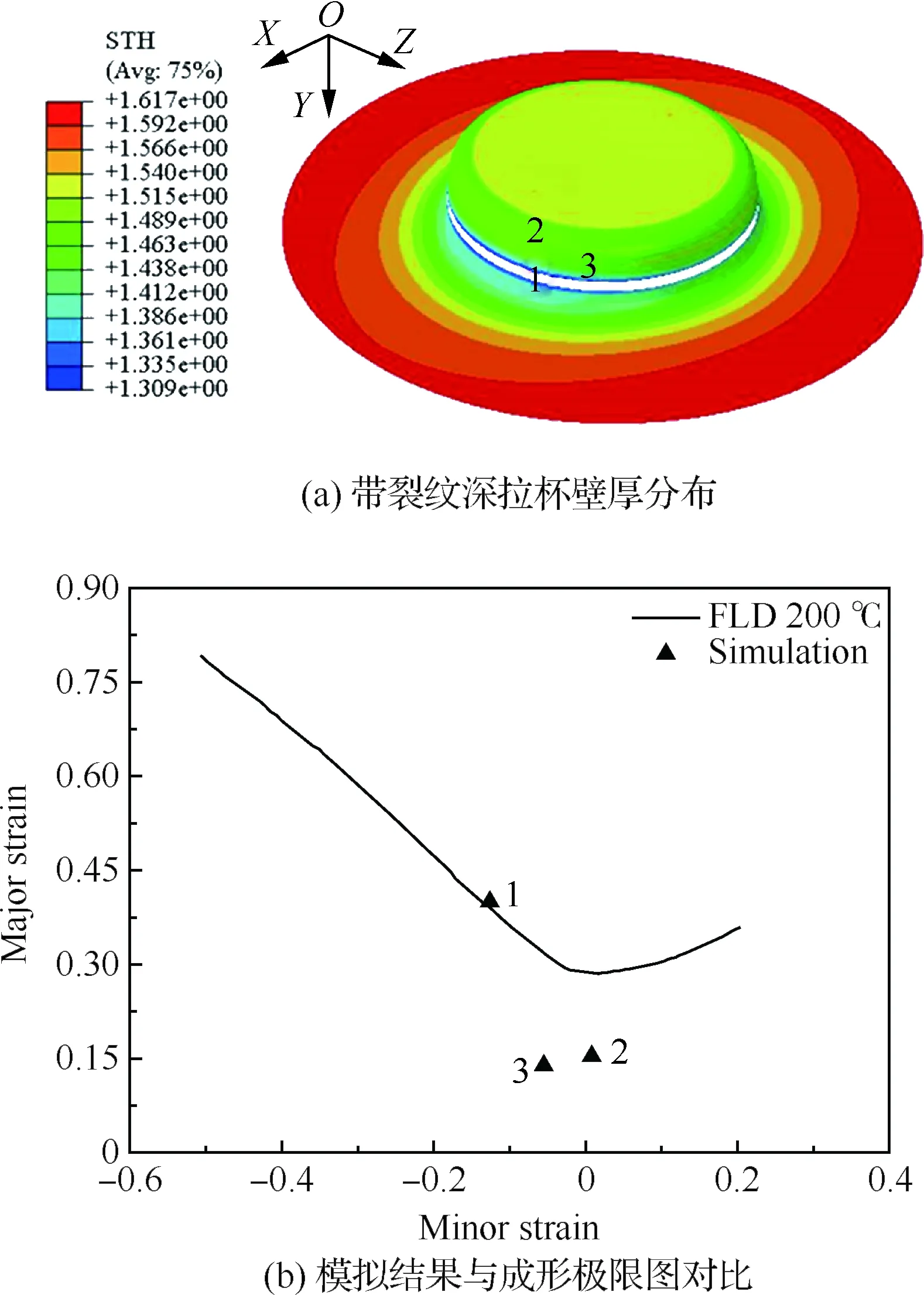
图5 200 ℃等温成形后带裂纹深拉杯厚度分布模拟结果及其与成形极限图的对比Fig.5 Simulation of thickness distribution of drawn cup with crack after deep drawing at 200 ℃ and its comparison with the forming limit diagram

图6 深拉成形壁厚分布及冲头力-位移曲线Fig.6 Thickness distribution in deep drawing and curves of punch force vs displacement

3.2 非等温成形热力耦合模拟

本节通过在考虑参数演化的各向异性屈服CPB06-GTN损伤模型编译的VUMAT子程序中加入温度相关变量，将子程序嵌入到ABAQUS软件中进行了非等温拉深成形热力耦合有限元模拟。在ABAQUS中提供了显示动态热力耦合分析步，可将VUMAT子程序应用于该分析步中，VUMAT子程序可根据单元节点的温度来调整材料参数，完成应力更新，并依据产生的塑性变形计算由塑性变形导致的温度升高，继而对温度变量进行更新。这里，设置镁合金板的单元为S4RT，该单元包含了温度自由度，而其他模具均设置为离散刚体，并施加温度边界条件。模具和压边圈温度设为245 ℃，冲头温度和板料初始温度分别为171 ℃和175 ℃。

在有限元模拟时，通过在模具上施加温度边界条件来控制模具的温度，镁合金板的热参数及与模具间的热传导率参数采用Lee等[26]给出的AZ31镁合金在200 ℃的热参数，具体数据如表5所示。变形过程中模具和镁合金板之间会发生热传递，在模拟时为了节省计算时间，提高了拉深速度；在温热成形时为了让模拟的温度与速度相匹配，也对镁合金与时间相关的材料参数进行了放大处理。由于对计算速度放大了100倍，这里对热传导率也放大了100倍。参考实验条件，对直径为228.6 mm的镁合金板，在对应拉深比为2.25，压边力为80 kN时的温热深拉非等温成形，进行了数值模拟。

当模具和压边圈温度为245 ℃，冲头温度为171 ℃时，能够顺利完成拉深成形，模拟的温度(NT11)和壁厚分布如图7所示。从图7(a)可看出，冲头与深拉杯的底部中心处温度约为171 ℃，而板被压边圈压紧部分的凸缘处温度则和模具及压边圈温度一致，约为245 ℃，侧壁温度在171～245 ℃之间。从图7(b)可看出，由于冲头温度较低，冲头圆角处强度较高，该处变薄并不严重，而侧壁则由于承受了较大的径向拉应力，导致了变薄。同时由于各向异性的影响，镁合金板在轧制方向(X轴方向)的侧壁变薄较严重。与前述等温成形的结果对比可以看出，非等温深拉成形可通过调整不同部位的温度，提高拉深比，改善拉深成形性能。

表5 AZ31镁合金的热物理性能参数Table 5 Thermophysical properties parameters of AZ31 magnesium alloy

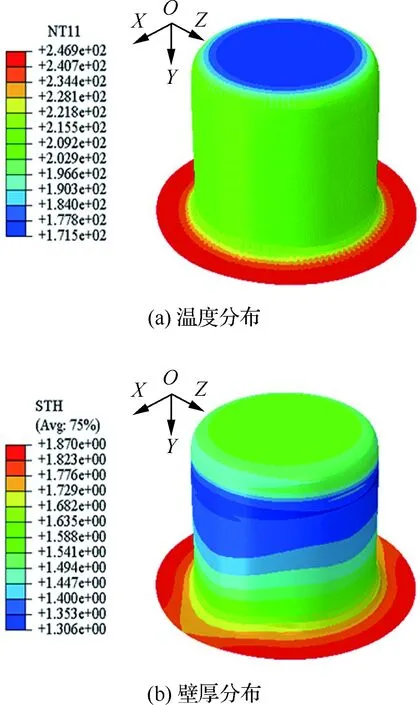
图7 非等温成形时的温度分布与壁厚分布Fig.7 Temperature distribution and thickness distribution in non-isothermal deep drawing forming

此外，还将非等温深拉成形模拟结果与已有实验数据[13]进行了对比。图8表示了深拉成形后沿轧制方向和横向的最大与最小主应变模拟结果及其与实验数据对比。图8中，横坐标表示深拉后不同区域距离深拉杯底部中心(以Pole表示)的距离，a区域为底部中心，b区域为冲头圆角处，c区域为侧壁区域，d区域为深拉杯的顶部区域；RD Major Strain-Experiment 表示实验测得的沿轧制方向的最大主应变分布，TD Minor Strain-CPB-GTN 表示采用CPB-GTN子程序模拟得到的沿横向的最小主应变分布，其余以此类推。由图8可以看出，模拟的最大与最小主应变同试验结果趋势基本一致，只是在横向最大主应变存在一定误差，这可能与较小应变测量时各向异性效应的忽略和较小应变测量的不确定性有关。

模拟预测的冲头力与位移关系曲线及其与实验结果对比如图9所示。由图9可以看出，模拟预测的冲头力与位移关系曲线的前半部分与实验结果吻合得很好，后半部分虽然存在一定的误差，但与没有考虑损伤的基于CPB06ex3ev屈服本构模型的模拟结果[13]相比，本节的非等温深拉成形模拟结果总体上比较精确，说明了考虑参数演化的各向异性屈服CPB06-GTN损伤模型子程序能够用于模拟镁合金的非等温成形过程。

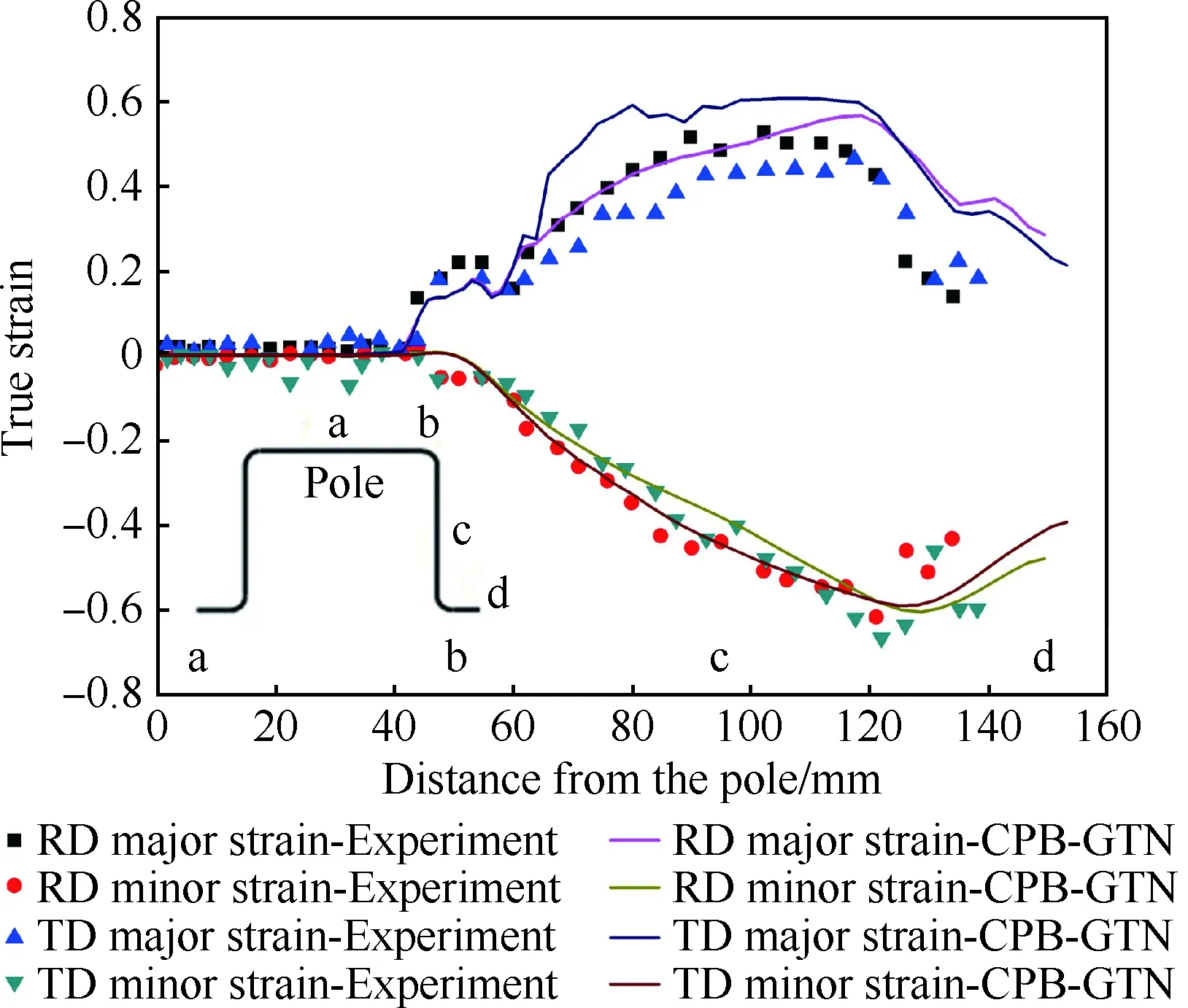
图8 沿轧制方向和横向的最大与最小主应变分布模拟预测及其与实验结果[13]的对比Fig.8 Simulation-based predictions of distribution of the maximum and minimum principal strain in rolling and transverse directions and their comparisons with experimental results[13]

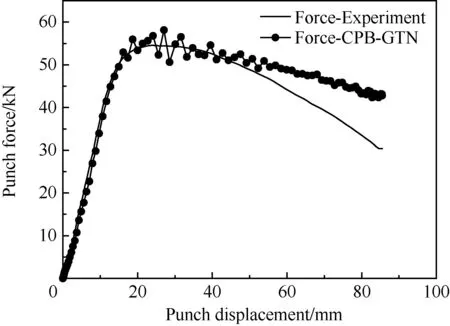
图9 冲头力与位移关系曲线的模拟预测及其与实验结果[13]对比Fig.9 Simulation-based prediction of punch force vs displacement curves and its comparison with experimental results [13]

4 结 论

1) 在GTN损伤模型的基础上，建立了考虑参数演化的各向异性拉压不对称屈服的CPB06-GTN损伤耦合模型，该模型不仅能够预测材料的损伤破坏，而且还能准确描述镁合金等HCP晶格结构材料的各向异性拉压不对称屈服及其在畸变硬化过程中的各向异性屈服面变化趋势。

2) 基于建立的镁合金板热成形各向异性屈服及损伤本构方程，同时考虑成形时的热、力耦合关系，编写了VUMAT子程序并嵌入ABAQUS/Explicit分析中，使用该子程序进行的等温及非等温成形数值模拟算例证明了所建立本构模型的正确性。

3) 同镁合金等温拉深成形相比，非等温拉深成形模拟结果表明，非等温拉深成形能够改善镁合金的成形性，提高镁合金的成形质量。

参 考 文 献

[1] 宋令慧, 王守仁, 赵宰炯. 连铸连轧镁合金AZ41微观结构与摩擦磨损性能[J]. 航空学报, 2014, 35(6): 1733-1739.

SONG L H, WANG S R, CHO J H. Microstructure and friction wear properties of twin-roll casting magneisum alloy AZ41[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1733-1739 (in Chinese).

[2] 唐荻, 王丹, 江海涛, 等. 异步轧制对 AZ31 镁合金组织及高温塑性的影响[J]. 塑性工程学报, 2013, 20(2): 78-83.

TANG D, WANG D, JIANG H T, et al. Effects of differential speed rolling process on microstructure and plastic deformation of magnesium alloy[J]. Journal of Plasticity Engineering, 2013, 20(2): 78-83 (in Chinese).

[3] 吴章斌, 桂良进, 范子杰. AZ31B 镁合金挤压材料的力学性能与本构分析[J]. 中国有色金属学报, 2015, 25(2): 293-300.

WU Z B, GUI L J, FAN Z J. Mechanical properties and constitutive analysis of extruded AZ31B magnesium alloy[J]. Chinese Journal of Nonferrous Metals, 2015, 25(2): 293-300 (in Chinese).

[4] 钟敏, 唐伟琴, 李大永, 等. AZ31B镁合金板材温热成形极限实验研究[J]. 塑性工程学报, 2011, 18(5): 59-63.

ZHONG M, TANG W Q, LI D Y, et al. Experiment research on forming limit diagram (FLD) of magnesium alloy sheet AZ31B at warm condition[J]. Journal of Plasticity Engineering, 2011, 18(5): 59-63 (in Chinese).

[5] 何维均, 张士宏, 程明, 等. 宏观弹塑性本构模型的研究进展[J]. 塑性工程学报, 2015, 22(3): 1-11.

HE W J, ZHANG S H, CHENG M, et al. Review on the development of macroscopic elastic-plastic constitutive models[J]. Journal of Plasticity Engineering, 2015, 22(3): 1-11 (in Chinese).

[6] HILL R. A theory of the yielding and plastic flow of anisotropic metals[C]∥Proceedings of the Royal Society of London Series A, Mathematical and Engineering Sciences. London: The Royal Society Publishing, 1948, 193(1033): 281-297.

[7] BARLAT F, LEGE D J, BREM J C. A six-component yield function for anisotropic materials[J]. International Journal of Plasticity, 1991, 7(7): 693-712.

[8] BARLAT F, MAEDA Y, CHUNG K, et al. Yield function development for aluminum alloy sheets[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(11): 1727-1763.

[9] BARLAT F, BREM J C, YOON J W, et al. Plane stress yield function for aluminum alloy sheets—Part 1: Theory[J]. International Journal of Plasticity, 2003, 19(9): 1297-1319.

[10] HOSFORD W F. Incorporating work hardening in yield loci calculations[C]∥Strength of Metals and Alloys. Aachen: Federal Republic of Germany, 1979, 775-780.

[11] CAZACU O, PLUNKETT B, BARLAT F. Orthotropic yield criterion for hexagonal closed packed metals[J]. International Journal of Plasticity, 2006, 22(7): 1171-1194.

[12] PLUNKETT B, CAZACU O, BARLAT F. Orthotropic yield criteria for description of the anisotropy in tension and compression of sheet metals[J]. International Journal of Plasticity, 2008, 24(5): 847-866.

[13] TARI D G, WORSWICK M J. Elevated temperature constitutive behavior and simulation of warm forming of AZ31B[J]. Journal of Materials Processing Technology, 2015, 221: 40-55.

[14] 郎利辉, 杨希英, 刘康宁, 等. 一种韧性断裂准则中材料常数的计算模型及其应用[J]. 航空学报, 2015, 36(2): 672-679.

LANG L H, YANG X Y, LIU K N, et al. A calculating model of material constants in ductile fracture criterion and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 672-679 (in Chinese).

[15] TENG B G, YUAN S J, CHEN Z T, et al. Plastic damage of T-shape hydroforming[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S2): s294-s301.

[16] 王瑞泽, 陈章华, 臧勇. 基于Gurson 模型的镁合金板材温热冲压成形研究[J]. 北京科技大学学报, 2014, 36(4): 459-466.

WANG R Z, CHEN Z H, ZANG Y. Thermal stamping formability of magnesium alloy sheet based on the Gurson model[J]. Journal of University of Science and Technology Beijing, 2014, 36(4): 459-466 (in Chinese).

[17] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part 1—Yield criteria and flow rules for porous ductile media[J]. Journal of Engineering Materials and Technology, 1977, 99(1): 2-15.

[18] NEEDLEMAN A, TVERGAARD V. An analysis of dynamic, ductile crack growth in a double edge cracked specimen[J]. International Journal of Fracture, 1991, 49(1): 41-67.

[19] KIM J, RYOU H, KIM D, et al. Constitutive law for AZ31B Mg alloy sheets and finite element simulation for three-point bending[J]. International Journal of Mechanical Sciences, 2008, 50(10): 1510-1518.

[20] STEWART J B, CAZACU O. Analytical yield criterion for an anisotropic material containing spherical voids and exhibiting tension-compression asymmetry[J]. International Journal of Solids and Structures, 2011, 48(2): 357-373.

[21] YOON J, CAZACU O, MISHRA R K. Constitutive modeling of AZ31 sheet alloy with application to axial crushing[J]. Materials Science and Engineering: A, 2013, 565: 203-212.

[22] WANG R, CHEN Z, LI Y, et al. Failure analysis of AZ31 magnesium alloy sheets based on the extended GTN damage model[J]. International Journal of Minerals, Metallurgy, and Materials, 2013, 20(12): 1198-1207.

[23] 陈志英, 董湘怀. 各向异性 GTN 损伤模型及其在板料成形中的应用[J]. 上海交通大学学报, 2008, 42(9): 1414-1419.

CHEN Z Y, DONG X H. The Anisotropic GTN Damage model and its application in sheet metal forming[J]. Journal of Shanghai Jiaotong University, 2008, 42(9): 1414-1419 (in Chinese).

[24] TARI D G, WORSWICK M J, WINKLER S. Experimental studies of deep drawing of AZ31B magnesium alloy sheet under various thermal conditions[J]. Journal of Materials Processing Technolog, 2013, 213(8): 1337-1347.

[25] LI W J, ZHAO G Q, MA X W, et al. Study on forming limit diagrams of AZ31B alloy sheet at different temperatures[J]. Materials & Manufacturing Processes, 2013, 28(3): 306-311.

[26] LEE S, HAM H J, KWON S Y, et al. Thermal conductivity of magnesium alloys in the temperature range from -125 ℃ to 400 ℃[J]. International Journal of Thermophysics, 2013: 34(12): 2343-2350.