剪切稀化非牛顿射流撞击液膜破碎直接数值模拟

朱呈祥，吴猛，陈荣钱，尤延铖

厦门大学 航空航天学院，厦门 361005

非牛顿射流撞击是液体火箭发动机中广泛采用的燃料雾化手段，但人们对撞击雾化过程中非牛顿黏性的改变及流态转变、流体剪切特征和喷注破碎品质之间的关联等仍知之甚少。目前国际上开展相关研究的有不少团队，其中Ciezki等[1]从2001年开始加入GGPT (German Gel Propulsion Technology)项目以来一直致力于非牛顿射流撞击的物理与流变雾化特性的研究。他们通过研究不同喷注速度下夹角为90°的双股射流撞击破碎特征，将其撞击雾化模态分为6类：射线型、边缘液滴型、无边缘型、液丝型、完全破碎型和颗粒状射线型[2]。在此基础上，Ciezki等[3]还针对非牛顿流体提出了一套较为可信的快速定位雾化模态的无量纲数判定方法。

Lee等[4]则重点研究了喷嘴几何尺寸和通用雷诺数对非牛顿破碎长度、小液滴尺寸与分布等雾化特征的影响,认为非牛顿射流撞击雾化可囊括为4种模态：预膜片型、射线型、液丝型和完全破碎型[5]。此外，Lee等还指出，以往人们在判断射流破碎模态时主要依据流体的韦伯数We和雷诺数Re(对于非牛顿流体为通用雷诺数)，然而这两个参数都没有考虑压力影响。由于气体压力的改变主要是影响它的密度，因此Lee等建议在定义韦伯数和雷诺数时其他参数保持不变，将液体密度换成气体密度，这样就能兼顾到压力的影响。他们利用新定义的两个无量纲参数分析了不同条件、不同流体的撞击雾化模态后发现，所有流动在模态上都表现出明显的规律性。国内开展非牛顿射流撞击破碎研究的也有不少团队，包括北京航空航天大学[6]、天津大学[7]、西安航天动力研究所[8]、南京理工大学[9]、西北工业大学[10]等单位。但是可以发现，以上团队主要都是开展实验或理论研究，而国际上有能力开展数值研究的团队并不多。

佐治亚理工Yang的团队[11]曾开展过非牛顿流体直接数值模拟(DNS)研究，但他们未能从非牛顿黏性的角度分析其在撞击形成液膜后的分布及变化，并进而剖析非牛顿撞击雾化的物理机制。德国斯图加特大学的Weigand等[12]对非牛顿流体开展过单喷嘴的雾化DNS分析，虽然该工作不涉及撞击雾化，但他们提出了基于本地非牛顿黏性的分析方法。此外，他们对射流内部的小涡流动捕捉极为精细，而且基于非定常时域分析提出了非牛顿流体的新凹穴破碎类型。在国内，第二炮兵工程大学的强洪夫等[13]一直致力于光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)模拟，这是一种纯Lagrange无网格粒子方法，可以对液滴运动实现精确模拟。但正如他们所言，SPH方法对射流撞击形成液膜至液膜破碎形成液滴的过程无法捕捉[14]，SPH的计算精度、稳定性和效率也仍有待提高。

因此，本文将采用DNS工具，针对低雷诺数和中等韦伯数条件下的非牛顿撞击射流开展液膜破碎特征及机理研究。首先将介绍采用的数值方法与设置，随后重点分析撞击液膜的三维结构和破碎特征，并讨论液膜内的非牛顿黏性变化，最后是对本文工作的总结。

1 数值方法

本文采用的是课题组自主开发的DNS程序Free Surface 3D(FS3D)，所求解的三维不可压Navier-Stokes方程组为

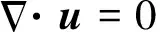
(1)

(2)

式中：u为速度矢量；ρ为密度；p为压力；t为时间；μ为黏性系数；k为外部作用力；T为气液两相分界面处的表面张力。FS3D程序采用流体体积(Volume of Fluid，VoF)[15]方法捕捉气液两相分界面，该方法定义变量f以表征单元格内的液体体积分数，其表达式为

(3)

(4)

为了精确描述气液两相分界面，FS3D程序运用分段线性界面计算(Piecewise Linear Interface Calculation，PLIC)[16]方法对界面进行重构。FS3D所采用的数值方法已在文献[17-18]中进行了气液两相液滴和瑞利破碎射流的实验验证，也说明了方法的可靠与准确性。

对于非牛顿黏性，本文采用幂律函数进行模拟，其表达式为

(5)

(6)

本文研究的非牛顿流体为20%质量分数Polyvinylpyrrolidone(PVP)水溶液。该液体的Deborah数(De)和Elasto-capillary数(Ec)都在10-8量级，远低于黏弹性流体的极限值0.35和2.35，因此是一种典型的剪切稀化幂律流体。表1给出了液体与气体的物性参数以及射流尺寸，其中D为喷管直径，u为速度，σ为表面张力系数，下标“l”和“g”分别代表液体与气体。此外，表1还给出了液体的韦伯数Wel与雷诺数Rel，其计算表达式为

(7)

本文采用如图1所示的方形计算域，xOz和yOz面的下边界均为无滑移壁面，射流以速度ul分别沿x轴和y轴正向喷入，其余边界设置为自由出流条件。为了求解湍流中的Kolmogorov尺度[24](选取湍流长度尺度为射流直径的1/10，脉动速度取为射流速度，可以估算Kolmogorov尺度为3.6 μm)，本文在长(L)×宽(W)×高(H)为40D×40D×40D的计算域内采用512×512×512的结构化网格，因此最小网格尺度为7.8 μm，与Kolmogorov尺度在同一量级。

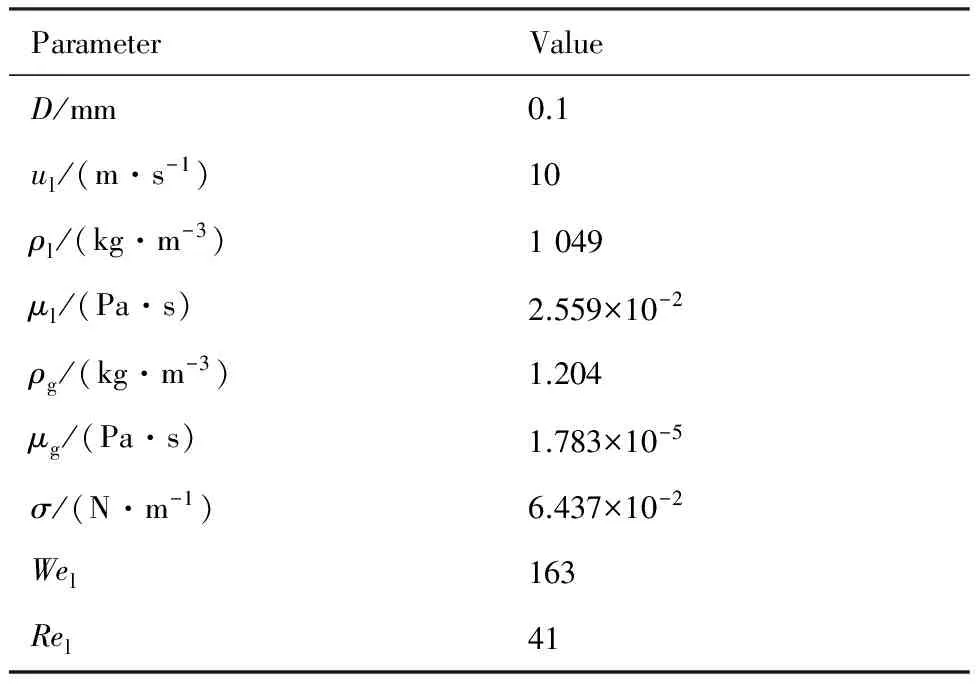
表1 计算参数设置Table 1 Summary of computational parameters

图1 非牛顿撞击射流计算域Fig.1 Computational domain for non-Newtonian impinging jets

2 射流结构

两股非牛顿射流撞击形成的典型液膜破碎结构如图2所示，其中U*=u/ul为无量纲速度。从直径为D的喷嘴中射出的非牛顿流体经90°正交撞击后形成近乎沿对角方向的拉伸薄液膜。该液膜不仅向撞击点下游迅速扩展，而且同样存在于撞击点上游，但其尺寸明显低于下游液膜。在图2所示时刻(无量纲时间t*=tul/D=41.4)，上游液膜长度Lr(定义为撞击点至后缘Rim中心的距离)仅为D。撞击点下游液膜为流动主要分析对象，从宏观上包含液膜、液丝和液滴结构。在距离撞击点Ls<11.5D的下游范围内，液膜较为完整，表现为中心薄膜迭加厚边缘结构，该边缘的厚度沿流向增加，其等效直径d随流向长度呈抛物线形发展并最终趋于一个与射流直径D在同一量级的恒定值。在更下游区域，液膜出现破碎，形成液丝与液滴结构，其中，液丝在表面张力作用下向两侧收缩，而卫星液滴主要聚集在对角中心线附近。液丝与边缘之间的液膜发生破碎，主要形成液丝结构。在该时刻，液膜破碎长度Lb(定义为液膜破碎处与射流头部Rim中心的距离)与Ls相当，为10.75D。

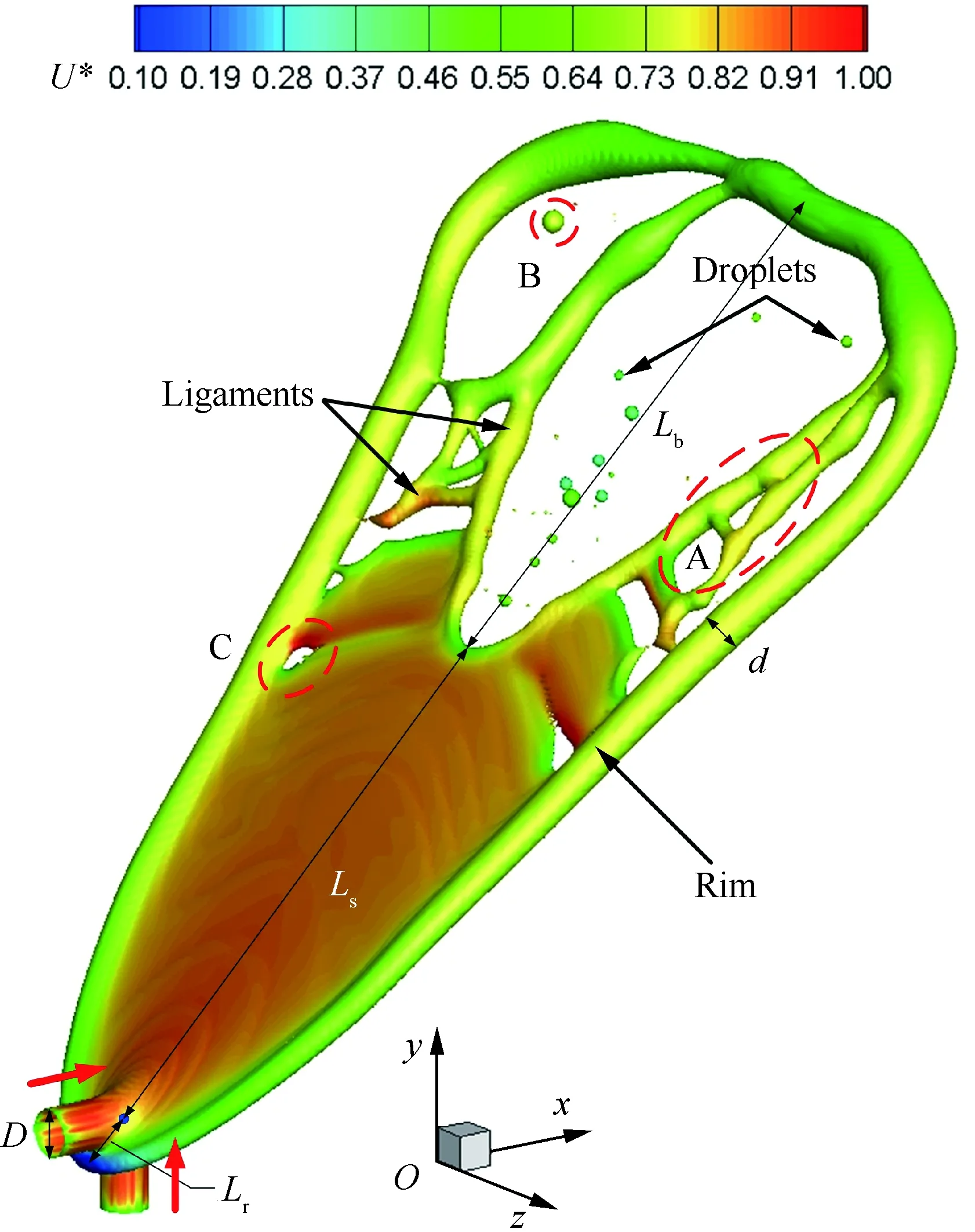
图2 撞击射流形成的液膜破碎典型结构(t*=t ul/D= 41.4)Fig.2 Typical structure of sheet breakup formed by impinging jet (t*=tul/D=41.4)

在该液膜破碎结构中，有几处值得特别关注。首先在A区，由液膜破碎而形成的液丝表面呈现明显的波动特征，这主要是因为液膜破碎产生的附加扰动作用在液丝上而产生Kelvin-Helmholtz不稳定。随着时间的进一步推移，该不稳定扰动将诱发液丝向液滴的破碎转变。在B区，可以观察到一个直径约0.46D的单液滴，相较对角中心线附近的卫星液滴而言，其尺寸明显较大，这是由于该液滴由液丝破碎而成，因此具备破碎前液丝的全部体积，只是受表面张力作用而收敛为球形，其具体形成机理将在之后详细介绍。在C区，可以发现液膜与厚边缘接触处刚开始出现破碎现象，该破碎口将随着时间发展不断撕裂液膜，使其向液丝转变。对比破碎口的上下游速度发现，下游液膜的速度显著高于上游速度，由于液膜本身具备沿对角方向的速度，在形成破碎口后，液膜将逐渐收缩其表面积，上游液膜逆流向回溯抵消部分液膜原始速度，而下游液膜顺流向加速，进而形成明显的速度差。此外，从Rim的速度分布可以发现，边缘沿流向具有先加速再减速的特征，具体表现为头部边缘速度较低，约为射流速度的1/2，中部边缘速度较高，约占射流速度的4/5，而后部边缘几乎滞止。事实上，这给出了两方面的启示:①边缘液体将向头部不断堆积，造成头部边缘的加厚及失稳，最终导致头部边缘的破碎；②后部边缘相对喷嘴的位置几乎固定，在后续的时域分析中可以更直观地体现这一点。

总的来说，在该典型液膜破碎结构中，可以观察到明显的边缘、液丝、液滴及不稳定表面波的生成，量化的数据和对流体局部速度的分析也有助于对该类破碎现象物理机制的理解。基于现有流动特征的分析，该撞击射流破碎应属于非牛顿流体的Open Rim类别，但遗憾的是，由于计算域限制，无法进一步观察和验证头部边缘的发展，这也是后续工作需要解决的问题。

液体表面积大小对射流撞击雾化十分关键，它直接决定了气液两相的有效接触面，因此对工程实际应用具有重大指导意义。图3为撞击射流全过程中液体表面积随时间变化的统计结果，其中图3(a)为绝对表面积S的时域规律，而图3 (b)为无量纲表面积S*的时域规律，本文定义S*为绝对表面积与双股圆柱射流的表面积之比,即S*=S/(πD2/4+πDult)。

从图3(a)显然可以发现，随着射流的不断流入，计算域内液体的绝对表面积也不断增加。但从增长斜率和横向辅助线可以看出，在射流初始阶段(t*<2.5)和本文计算的终止时刻附近(t*>35)，表面积的增长趋势较为缓慢，而在中间阶段表面积增长相对较快。这其实与撞击射流液膜破碎的流场结构是密切相关的，在初始阶段，双股射流各自喷出后，表面积的增加与时间呈线性关系，从发生碰撞至形成液膜的过程中，由于射流融合的存在，表面积增速放缓。但随着液膜的形成和大面积铺开，液体的表面积快速增长直至液膜破碎的发生，此时，局部流场由液膜向液丝过渡，相应表面积也开始收缩，但其减少量相较液膜的扩展以及流体的不断补充仍是小量。随着液膜的继续破碎，总表面积增速也进一步减缓。在图3(b)中，以上特征可以得到更直观的体现。无量纲表面积S*从本质上反映的是平均单位液体的面积变化规律，在射流初始阶段由于撞击的发生及液膜仍未形成，因此无量纲面积呈下降趋势，但随着液膜形成带来的面积增加效应，使得S*快速增加，至t*=24达到极值1.9，表明单位液体的表面积相较圆柱射流而言扩张了1.9倍。此后，由于液膜破碎的发生，由液膜形成带来的面积增加效应已经无法抵消由液膜破碎带来的面积减小效应，因此S*逐渐下降。

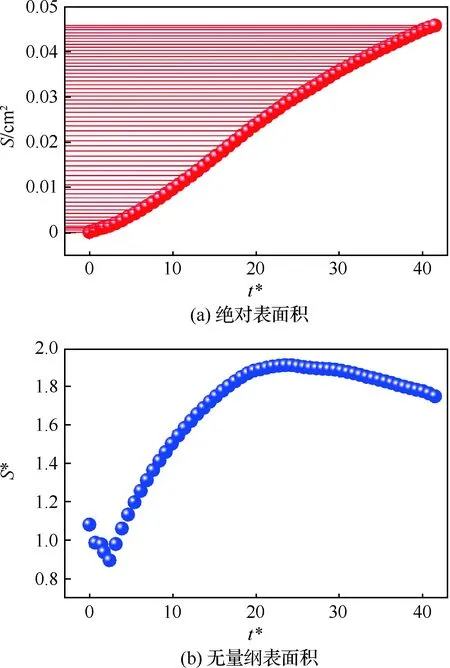
图3 液体表面积随时间的变化Fig.3 Temporal development of surface area of liquid

液体总表面积的时域变化需要统计液膜、液丝、液滴及边缘的各自表面积，在实验中很难对其定量测量，而数值方法能够深入流体内部对其时域及空域问题进行研究，进而分析各类流动特征的物理本质，这也是其优越之处。

3 流动特征及机理分析

为了分析非牛顿撞击射流的流动机理，图4给出了t*=16.2时刻液膜结构的无量纲速度及无量纲涡量场(ω*=ωD/ul,ω为涡量)特征，其中α为对角流向，β为垂直于α的方向。图中黑色实线均为气液两相边界面。此时，非牛顿撞击射流形成的液膜仍处于完整形态，图4(a)为液膜在对角面内的形状，可以发现其沿A′-A′ 截面基本呈对称分布，但值得指出的是，图中右下角的气液两相分界线实际上并不代表此刻液膜出现了破碎，这只是因为三维液膜在空间上不完全位于对角平面内，而是沿x轴存在轻微扭转，这从图4(c)的B′-B′截面中也可以得到体现。从速度分布可以发现，在液体内部，撞击点速度近似为0，液膜边缘的速度较小而中心较高，速度极值出现在撞击点下游3D位置附近。在撞击点，射流由于对撞而滞止，但在其下游，液体由于迅速扩展释放堆积的质量流量而形成液膜，导致局部高流速的出现。再下游的液膜扩张主要依赖于流体惯性，其对快速释放流量的需求并不迫切，因此速度沿流向逐渐下降。值得注意的是，在液膜后缘，由于后部Rim几乎滞止，因而此处流体速度也极低。

在图4(b)中，可以观察到双股射流形成的头部Rim横截面呈水滴形，其最大厚度dr接近0.8D，而撞击点上游形成的后部Rim横截面呈圆柱形，其最大厚度仅为射流直径的约1/3，二者相差较为悬殊。从第2节分析知道，边缘厚度从后部到前部沿对角流向呈抛物线增长，据此可以定量判定撞击液膜各流向截面的边缘厚度变化规律。通过方程拟合，该抛物线应满足：dr/D=0.267+0.042(α/D)-0.000 4(α/D)2，其中，α=1.25D对应后部边缘厚度，α=12D对应头部边缘的厚度。统计撞击形成的液膜厚度沿流向的变化规律可知，在撞击点到头部边缘之间，液膜厚度ds呈幂函数下降，满足的规律为ds/D=5.3·(α/D)-1.58，α=3D位置处液膜厚度与射流直径相当，而α=10D处液膜直径降为约0.15D。此外，从图中的涡量分布还能发现，在该类撞击射流气液两相场中，涡量主要集中在液体周围的气相中，事实上，涡量本质上反映的是流体剪切程度，相较气体而言，液体由于黏度较大其剪切程度必然较小。在射流喷注口及撞击点和头部边缘附近，气体的涡量较高，而沿着液膜表面的涡量沿流向降低，代表其对气体的影响也逐步减弱。

图4(c)为B′-B′ 截面的二维液膜轮廓，显然它与z轴存在轻微的1.5°扭转角，液膜在等x截面内的厚度较为均匀，为0.27D，考虑到撞击液膜的对角特性，其实际厚度仅为D/5。在液膜两侧堆积的边缘呈对称骨状分布，其最大厚度与图4(b)中的头部边缘厚度已基本相当。此外，观察涡量场分布可以发现，边缘外侧的气流存在较大涡量，而液膜表面附近气流的涡量相对较弱。

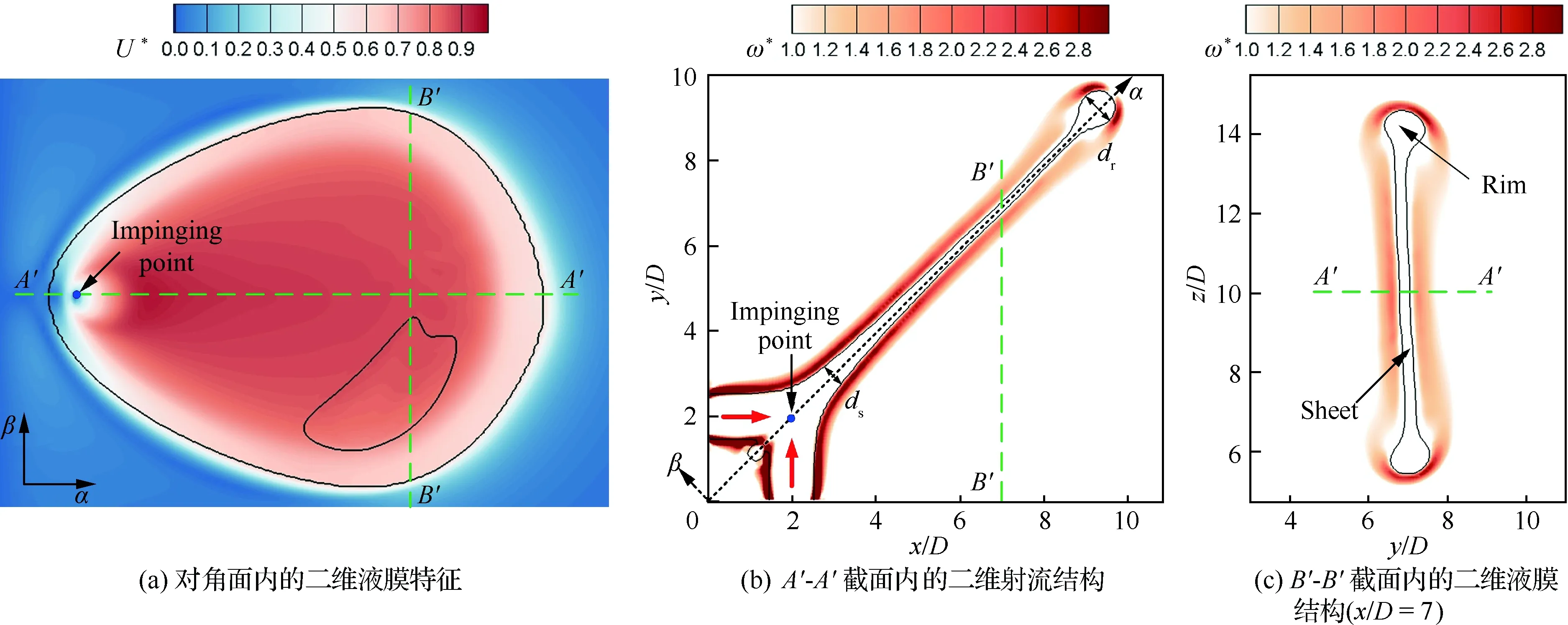
图4 t*=16.2时刻撞击射流液膜的结构特征Fig.4 Flow structure of impinging liquid sheet at t*=16.2

图5给出了液膜破碎过程中细节流动特征的时域变化，其中，蓝色虚线区F代表的是液丝与边缘的融合过程，而红色虚线区E显示了第2节提及的液丝向液滴的转变过程。首先，在F区，液膜破碎形成的液丝在t*=33.0时刻一端与边缘相连，而另一端刚与主液丝断开，表现为尖锥状，其尖头部在表面张力的作用下具有高回溯速度，到t*=34.2时刻该液丝收缩为类圆柱形，并不断向边缘汇拢。至t*=35.4时刻，该液丝仅能观察到微小头部，而大部分已与边缘融为一体。随着时间的进一步推进，该液丝在t*=39.0时刻已被边缘完全吸收。值得注意的是，尽管该液丝速度明显高于边缘的速度，但由于其尺寸较小，因此融合过程并未对边缘的形状和运动产生影响。

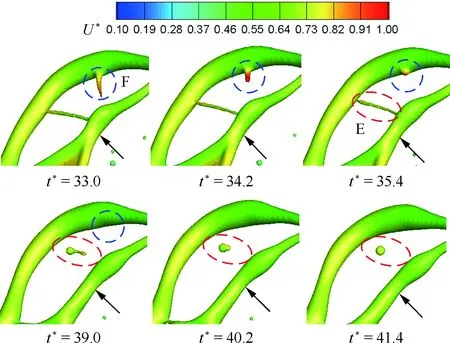
图5 液膜破碎过程产生的液丝与边缘融合及液丝向液滴的转变Fig.5 Ligament collision and ligament-to-droplet transition during liquid sheet breakup process

图6为三维撞击射流液膜在yOz面内的投影随时间的变化规律，其图谱颜色代表无量纲速度U*，液膜扩张半角为θ(定义为从射流喷注口的切线边缘至撞击射流液膜边缘的最大角度)，后部液膜在yOz面内的投影长度为Lr。显然，随着时间的推进，撞击射流液膜不断铺开，其扩张半角也逐渐增加，从t*=4.2时刻的28°发展到t*=17.4时刻的42.2°，如图6中的左上图所示。但同时可以发现，液膜的扩张半角并不会一直无限制增长，在经过一段快速增长后将逐渐变缓并趋于某一定值，该值由流体物性和撞击射流参数共同决定，在本文的正交撞击条件下，该恒定值约为43°。

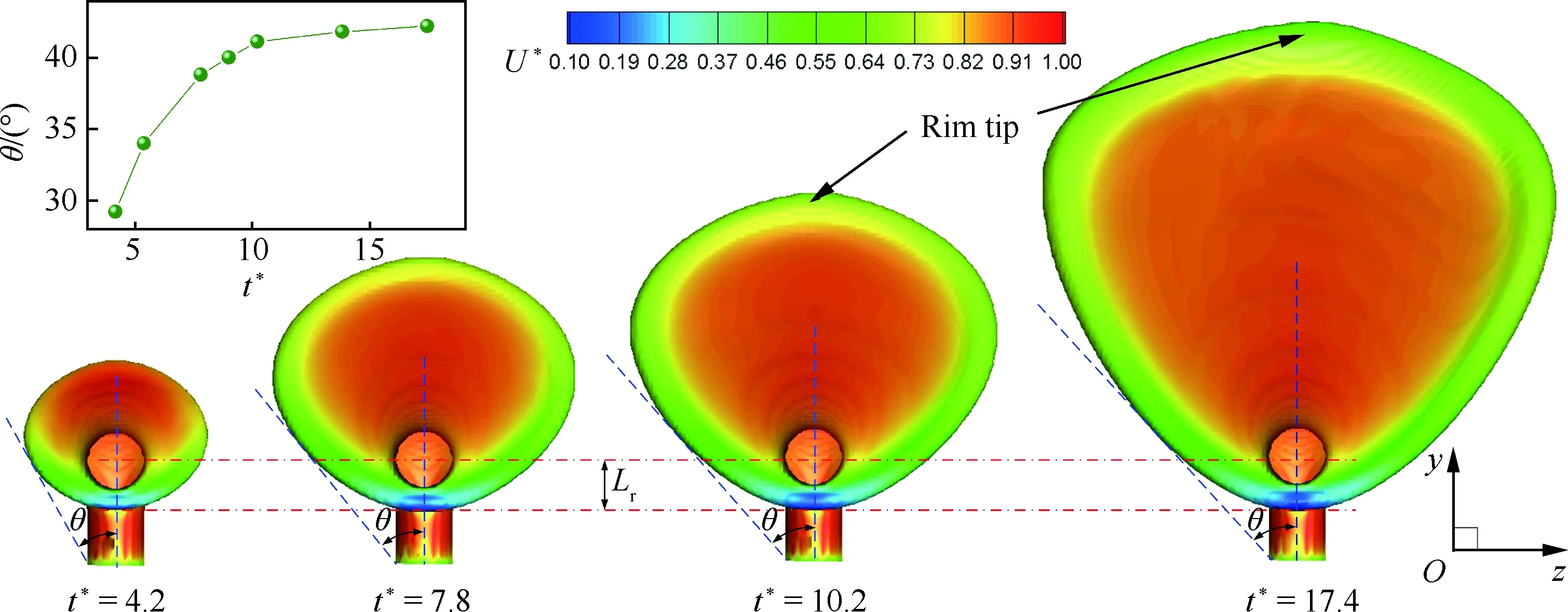
图6 撞击射流液膜及其扩张半角的时域变化Fig.6 Temporal development of impinging liquid sheet and its expansion half-angle

在图6中，还有几处值得特别注意。首先,后部液膜的长度Lr，从t*=4.2开始，尽管液膜本身不断向下游发展，但后部液膜的长度Lr几乎恒定地保持在一倍射流直径左右，说明Lr与液膜的扩张与否无关，而仅与射流条件和物性相关。其次，撞击液膜在t*=17.4之前具有高度左右对称性，液膜边缘的厚度也左右对称。但前文提到，一旦液膜出现破碎，气体力的作用将会打破这一平衡，不仅左右两侧的液膜破碎形态不同，而且液膜将呈现一定的空间扭曲。最后，液膜头部边缘的形成是一个渐进过程，t*=4.2时，液膜头部还未形成边缘，大量液体流量在撞击过程中的堆积使其快速扩张变得非常迫切，因此头部液膜的速度相对较高，而在t*=7.8～17.4的过程中，头部边缘逐步形成并不断加厚，速度也逐渐下降。

4 非牛顿特性

图7给出的是t*=41.4时刻撞击射流对角平面内的液膜形状及无量纲黏性系数分布。由于本文喷注的是剪切稀化流体，因此随着液膜形成而带来的剪切效应，液体的黏性系数逐渐下降。在图7(a)中，可以很明显观察到，随着液膜沿对角流向拉伸变薄，其黏性系数基本呈下降趋势，但表现出一定的非规律性，譬如液膜黏性存在先下降后上升再下降的过程。这一方面是因为二维液膜切面与三维液膜中面并不完全吻合，另一方面也反映了撞击对角液膜存在一定的表面波动。此外，在撞击点上游，流体的黏性也出现明显降低，这表明后部液膜尽管长度很短并且基本保持不变，但同样存在流体流动和剪切效应，只是相对下游液膜而言其剪切率较小。在液膜边缘内，流体黏性均维持在较高水平，尤其是头部与后部边缘的无量纲黏性系数接近1，这表明边缘内部几乎无剪切。

图7(b)为C′-C′ 沿线的黏性系数分布规律，显然，在x/D=0.4位置附近流体的无量纲黏性系数甚至低于0.2，表明该处流体的剪切率削弱了至少80%的流体黏性，因此，相较其他区域也更易发生破碎。随后，流体黏性快速升高至0.7以上又快速下降，这意味着局部存在高低交替剪切区，对应于第2节提及的液膜表面波。

图7 t*=41.4时刻撞击射流对角平面内的无量纲黏性系数分布Fig.7 Disbtribution of non-dimensional viscosity coefficient in diagonal plane of impinging jet at t*=41.4

5 结 论

采用DNS方法研究了低Re和中等We下的非牛顿射流正交撞击液膜破碎，得到以下主要结论：

1) 双股圆形射流在本文正交撞击条件下形成的液膜破碎属于Open Rim类别。

2) 液体总表面积随时间不断增长，但S*随液膜破碎的发生而下降，其极值为1.9，即单位液体的表面积相较圆柱射流扩张1.9倍。

3) 液膜边缘厚度沿流向呈抛物线性增长，而液膜自身厚度沿流向呈幂函数下降。

4) 液膜的破碎过程伴有液丝与边缘的融合，液丝向液滴的转变等时域流动特征。

5) 液膜的扩张半角随时间先快速增长后逐渐放缓并最终趋于恒定值43°，而射流撞击形成的上游液膜长度几乎不随时间发生变化。

6) 非牛顿射流内部存在明显的剪切稀化特性，液体内部最低黏性系数仅为零剪切黏性系数的20%。

致 谢

本文部分工作是在德国斯图加特大学完成，因此特别感谢Bernhard Weigand教授和Moritz Ertl博士的帮助与讨论，也要感谢斯图加特高性能计算中心对本工作的大力支持。

参 考 文 献

[1] CIEZKI H K, NEGRI M, HURTTLEN J, et al. Overview of the german gel propulsion technology program: AIAA-2014-3794[R]. Reston, VA: AIAA, 2014.

[2] KAMPEN J, MADLENER K, CIEZKI H K. Characteristic flow and spray properties of gelled fuels with regard to the impinging jet injector type: AIAA-2006-4573[R]. Reston, VA: AIAA, 2006.

[3] MADLENER K, CIEZKI H K, KAMPEN J, et al. Characterization of various properties of gel fuels with regard to propulsion application: AIAA-2008-4870[R]. Reston, VA: AIAA, 2008.

[4] RAMASUBRAMANIAN C, NOTARO V, LEE J G. Characterization of near-field spray of nongelled- and gelled-impinging doublets at high pressure[J]. Journal of Propulsion and Power, 2015, 31(6): 1642-1652.

[5] FAKHRI S, LEE J G, YETTER R A. Atomization and spray characteristics of gelled-propellant simulants formed by two impinging jets: AIAA-2009-5241[R]. Reston, VA: AIAA, 2009.

[6] YANG L J, FU Q F, QU Y Y, et al. Breakup of a power-law liquid sheet formed by an impinging jet injector[J]. International Journal of Multiphase Flow, 2012, 39: 37-44.

[7] 夏振炎， 李珍妮， 李建军， 等， 撞击式射流破碎特性的实验研究[J]. 天津大学学报， 2016, 49(7): 770-776.

XIA Z Y, LI Z N, LI J J, et al. An experimental study on breakup characteristics of impinging jets[J]. Journal of Tianjin University, 2016, 49(7): 770-776 (in Chinese).

[8] 杨伟东， 张蒙正. 凝胶推进剂流变及雾化特性研究与进展[J]. 火箭推进， 2005, 31(5): 37-42.

YANG W D, ZHANG M Z. Research and development of rheological and atomization characteristics of gelled propellants[J]. Journal of Rocket Propulsion, 2005, 31(5): 37-42 (in Chinese).

[9] 邓寒玉， 封锋， 武晓松, 等. 基于扩展TAB模型的凝胶液滴二次雾化特性研究[J]. 推进技术， 2015, 36(11): 1734-1740.

DENG H Y, FENG F, WU X S, et al. Characteristics of second atomization for gelled droplet based on extended TAB model[J]. Journal of Propulsion Technology, 2015, 36(11): 1734-1740 (in Chinese).

[10] XIAO H, SHI Y, XU Z, et al. Atomization characteristics of gelled hypergolic propellant simulants[J].International Journal of Precision Engineering and Manufacturing, 2015, 16(4): 743-747.

[11] MA D J, CHEN X D, KHARE P, et al. Atomization patterns and breakup characteristics of liquid sheets formed by two impinging jets: AIAA-2011-0097[R]. Reston, VA: AIAA, 2011.

[12] ZHU C X, ERTL M, WEIGAND B. Numerical investigation on the primary breakup of an inelastic non-Newtonian liquid jet with inflow turbulence[J]. Physics of Fluids, 2013, 25(8): 083102.

[13] 刘虎， 强洪夫， 韩亚伟， 等. 幂律型凝胶推进剂射流撞击雾化SPH模拟[J]. 推进技术， 2015， 36(9): 1416-1425.

LIU H, QIANG H F, HAN Y W, et al. SPH simulation of atomization characteristics of power-law gelled propellant formed by two impinging jets[J]. Journal of Propulsion Technology, 2015, 36(9): 1416-1425 (in Chinese).

[14] 刘虎， 强洪夫， 王广. 凝胶推进剂射流撞击雾化研究进展[J]. 含能材料， 2015， 23(7): 697-708.

LIU H, QIANG H F, WANG G. Review on jet impinging atomization of gelled propellant[J]. Chinese Journal of Energetic Materials, 2015，23(7): 697-708 (in Chinese).

[15] HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics, 1981, 39(1): 201-225.

[16] RIDER W J, KOTHE D B. Reconstructing volume tracking[J]. Journal of Computational Physics, 1998, 141(2): 112-152.

[17] SCHLOTTKE J, WEIGAND B. Direct numerical simulation of evaporating droplets[J]. Journal of Computational Physics, 2008, 227(10): 5215-5237.

[18] GOMMA H, KUMAR S, HUBER C, et al. Numerical comparison of 3D jet breakup using a compression scheme and an interface reconstruction based VOF-code[C]∥24th ILASS-Europe, 2011.

[19] MOTZIGEMBA M, ROTH N, BOTHE D, et al. The effect of non-Newtonian flow behavior on binary droplet collisions: VOF-simulation and experimental analysis[C]∥18th ILASS-Europe, 2002.

[20] FOCKE C, BOTHE D. Computational analysis of binary collisions of shear thinning droplets[J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(14-15): 799-810.

[21] SCHRÖDER J, LEDERER M L, GAUKEL V, et al. Effect of atomizer geometry and rheological properties on effervescent atomization of aqueous polyvinylphrrolidone solution [C]∥24th ILASS-Europe, 2011.

[22] 朱呈祥， 尤延铖. 横向气流中非牛顿液体射流直接数值模拟[J]. 航空学报， 2016, 37(9): 2659-2668.

ZHU C X, YOU Y C. Direct numerical simulation of a non-Newtonian liquid jet in crossflow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2659-2668 (in Chinese).

[23] 朱呈祥， 陈荣钱， 尤延铖. 低韦伯数非牛顿射流撞击破碎直接数值模拟[J]. 航空学报， 2017, 38(8): 120764.

ZHU C X, CHEN R Q, YOU Y C. Direct numerical simulation of impinging jet breakup with non-Newtonian properties at low Weber number[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(8): 120764 (in Chinese).

[24] BATCHELOR G K. The theory of homogeneous turbulence[M]. Cambridge: Cambridge University Press, 1953: 133-168.

[25] QIAN J, LAW C K. Regimes of coalescence and separation in droplet collision[J]. Journal of Fluid Mechanis, 1997, 331(1): 59-80.