自适应笛卡尔网格超声速黏性流动数值模拟
唐志共,陈浩,毕林,袁先旭
中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
随着计算流体动力学在工程实际中的深入应用,所面临的几何外形和流场越来越复杂,高质量的网格生成也变得越来越困难,往往需要占用大量人力资源。在针对复杂外形的网格生成方法中,相对于传统的分区结构网格方法和非结构网格生成方法[1-3],自适应笛卡尔网格[4-6]在自动化生成高质量网格方面具有很大优势。此外,自适应笛卡尔网格还具备天然的多重网格特性,可以在计算中加速收敛;无需存储矩阵、运算操作少,有利于高精度算法的应用。自20世纪80年代以来,计算机技术和性能的飞速发展促使了自适应笛卡尔网格技术的应用和推广,鉴于上述优势,越来越多的CFD工作者投入到该方法技术的研究和使用之中。
自适应笛卡尔网格生成技术的主要不足之处在于黏性物面边界处理较复杂,这是由笛卡尔网格的非贴体特性导致的。笛卡尔网格一般与物面相交,产生不同形状的切割单元。这些切割单元有的尺寸很小,容易引起在物面附近解的非物理振荡,如果数值模拟过程中采用的差分格式是显式的,还会限制时间步长以及影响计算的稳定性。目前主要的处理方法有:混合网格方法(Hybrid Cell Method)[7-8]、切割单元方法(Cut Cell Method)[9-10]、嵌入边界方法(Embedded Boundary Approach)[11]以及浸入边界方法(Immersed Boundary Method)[12-13]。
目前,基于自适应笛卡尔网格的超声速黏性流动数值模拟尚未工程实用化,有进一步发展的需求。为了实现对二维含强间断的高超声速黏性流动问题自动、高效、高精度的模拟,本文发展了自适应笛卡尔网格生成技术,以及笛卡尔网格下可有效模拟黏性物面边界条件的方法,并构建了相应的黏性数值求解器。
1 网格自适应技术
1.1 四叉树数据结构
在四叉树数据结构中,父亲网格单元加密得到4个子网格单元,父单元和子单元通过指针建立联系,如图1所示。这种数据结构存储量较小,自适应加密和粗化时方便高效:粗化时,只需将4个子指针置空,设为无指向即可;加密时,则只要对子指针分别分配内存,并指向子单元。
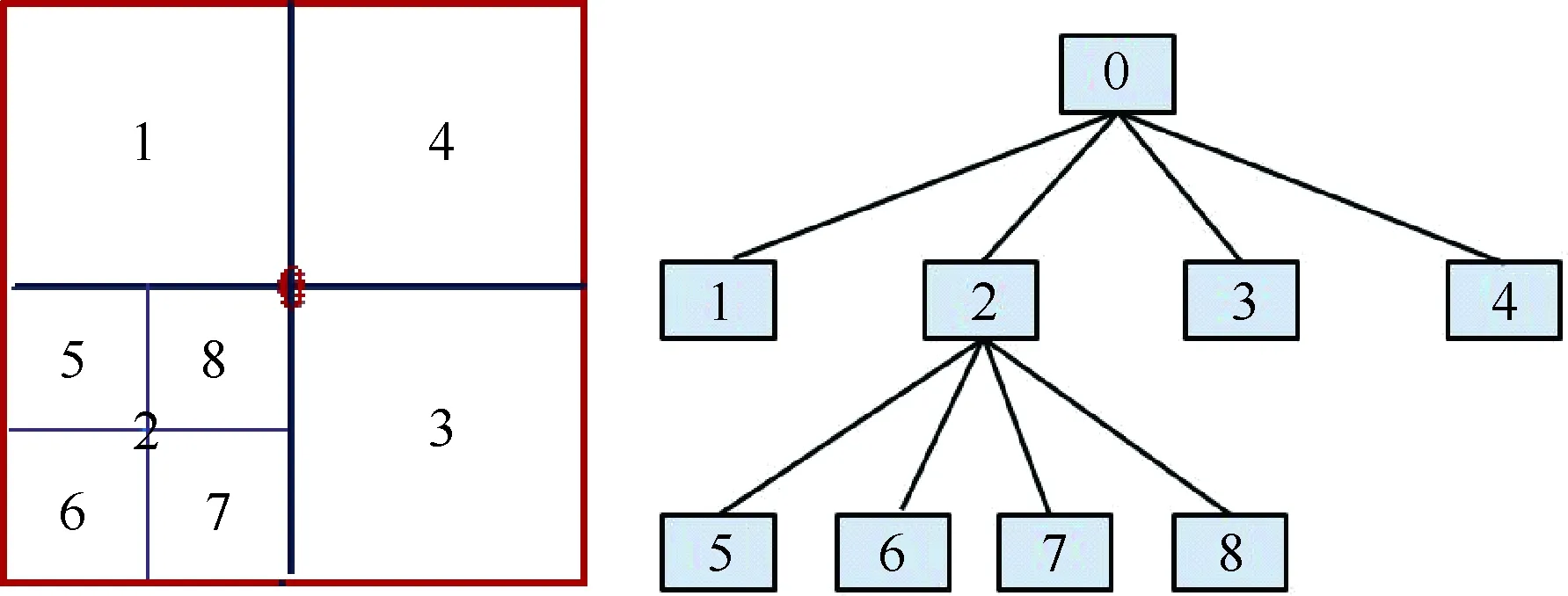
图1 四叉树数据结构Fig.1 Quadtree data structure

图2 网格信息存储Fig.2 Grid information storage
1.2 几何自适应
几何自适应加密是根据物体几何特征进行自适应加密,要求能够准确反映模型的外形结构特征。主要从两个方面进行:首先,基于物体几何外形,将与物面相交的网格单元进行一定次数的加密,得到初步的加密网格单元,如图3(a)所示;接着,基于物体表面曲率,在物体表面曲率变化较大的位置进行进一步加密,如图3(b)所示。此外,对于相交单元邻近的单元也需要进行一定次数的加密,以确保网格过渡均匀。对于表面曲率,通过相邻单元内物面曲率变化来判断,判据为:|kcell-kcell_neighbor|>Δk,kcell和kcell_neighbor分别代表目标单元和相应的邻近单元内的物面曲率,Δk一般不大于0.1,具体数值根据网格加密需求确定。

图3 几何自适应加密网格Fig.3 Grid adaptation based on geometric feature
1.3 流场自适应
在流场计算到一定程度后,还需要根据流场解的特征进行自适应。为了较好地捕捉流场中的激波、剪切层等特征结构,本文将速度的散度和旋度判据相结合来进行流场解自适应[14],其中速度的散度主要用来捕捉激波,速度的旋度则主要用于剪切层的捕捉。网格单元的速度散度Dcell和旋度Rcell可表示为
(1)
(2)
式中:l为单元cell的边长;系数a为给定值,二维时取2,三维时取3。
流场解自适应过程中需要对每个单元进行速度的散度和旋度计算,令计算域内所有网格单元的总数记作N,在得到N个单元的Dcell以及Rcell之后,可得到速度散度的标准差SD以及速度旋度的标准差SR,即
(3)
(4)
如果Dcell>δ1SD或者Rcell>δ2SR,则该网格单元需要加密;如果Dcell<0.1α1SD且Rcell<0.1α2SR,则该网格单元需要粗化。对于系数δ1、δ2、α1、α2的选取要结合流场特性给出[4],这是由于不同情况下流场中占主导地位的流动现象也是不同的。如果流场中没有明显主导的流动特征,则上述系数可以都取1;若流场中剪切层的作用较大,激波作用较小,则相应的系数可以取α1=δ1=2,α2=δ2=0.5;反之,若激波的作用较大,剪切层的作用较小,则可以取α1=δ1=0.5,α2=δ2=2。这些系数可能并不是最佳值,在具体流场计算中还需要根据流场特征进行调整,以使自适应后的网格分布更加合理。
2 Navier-Stokes方程数值求解器
2.1 方程离散
针对二维Navier-Stokes方程:
(5)
式中:E、F为无黏流项;Ev、Fv为黏性流项。
为了避免激波间断附近的非物理振荡,对于对流项的离散采用张涵信院士构造的无波动、无自由参数的耗散差分(NND)格式,即[15]
(6)
式中:minmod为限制器;本文E±采用Van Leer通量分裂[16]计算。
黏性项的离散采用中心差分格式,时间上则采用二阶Runge-Kutta方法[17-18]:
(7)
式中:R(U)为网格单元的残差。该格式要具备总变差衰减(Total Variation Diminishing,TVD)性质还需要满足稳定性约束条件:
(8)
式中:C为柯朗(Courant)数;Δt为当地时间步长;Δx为网格单元步长。式(8)为柯朗-弗里德里奇-列维(CFL)条件,在空间、时间均为二阶精度的情况下,常量const取值为1。
通过上述工作,本文针对Navier-Stokes方程构造的全离散格式具有二阶精度,保持TVD性质,可以避免激波间断附近的非物理振荡。
2.2 悬挂网格
在网格自适应之后,对于粗细网格的过渡区域,计算模版点流场值的获取需要特殊处理,即处理悬挂网格问题。悬挂网格问题分为两类:
第1类,计算模板点具有子单元。以图4为例,对于目标单元Ω,它的计算模板点X具有叶子单元,并非叶子结点,X的流场值的获取需要通过子单元插值得到,即
(9)
式中:qa、qb、qc、qd和qX分别代表网格单元a、b、c、d和X处的流场值,r1、r2、r3、r4分别为网格单元a、b、c、d与网格单元X中心点之间的距离。
第2类,计算模板点并非网格单元。以图5为例,对于目标单元Ω,它的最右侧计算模板点并非完整的网格单元,而是叶子单元L的一部分。在这种情况下,就需要对L进行剖分,以确定计算模板点L1的位置信息,再通过邻近单元插值方法获取L1处的流场信息,即
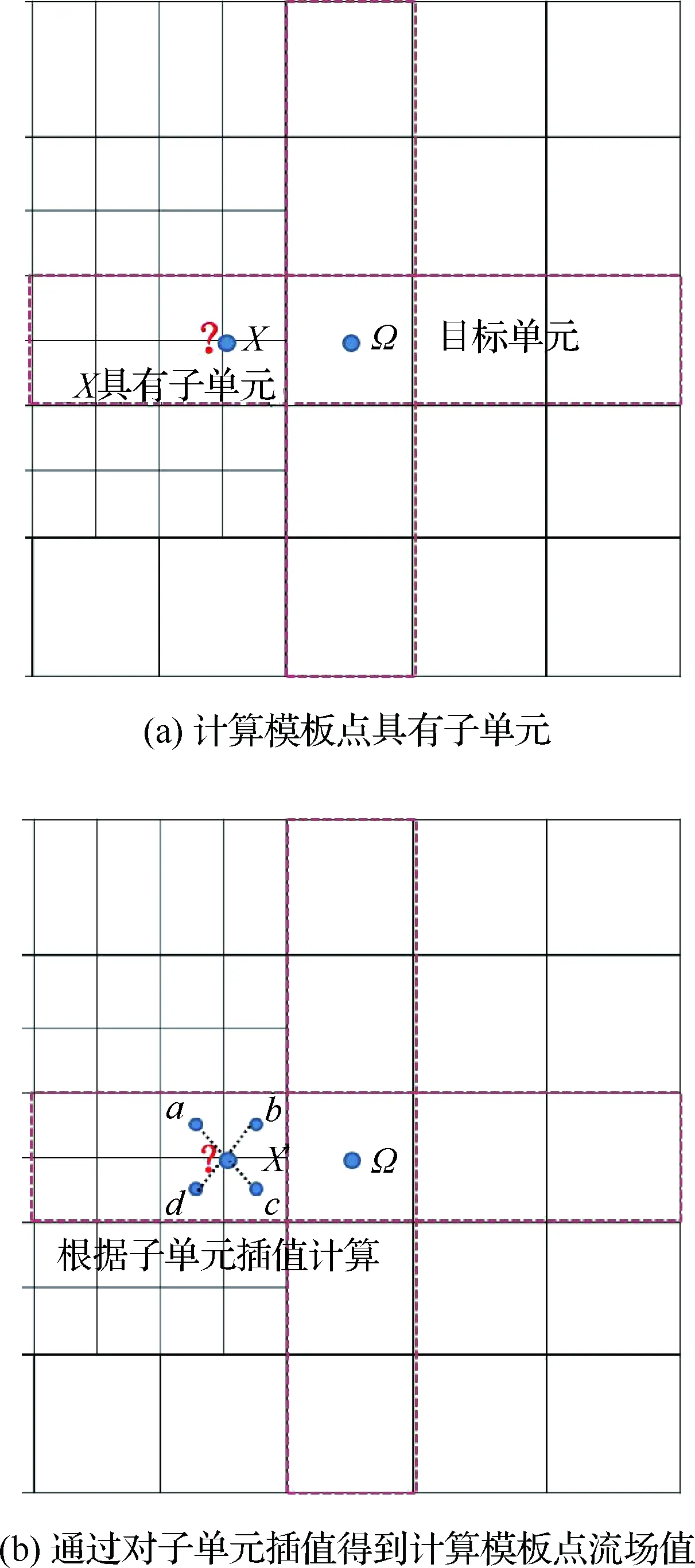
图4 第1类悬挂网格问题Fig.4 First type of hang-grid problem

(10)

图5 第2类悬挂网格问题Fig.5 Second type of hang-grid problem
3 物面边界处理
3.1 虚拟镜像对称方法
对于自适应笛卡尔网格,在物面边界附近进行插值计算时,可能需要用到物体内部的单元,即虚拟单元(Ghost Cell)。对于这些单元流场值的获取,需要采用虚拟镜像对称方法。以图6为例,为了获得虚拟单元A的流场值,首先要确定A在流场中的镜像点MA,通过邻近单元插值的方法获得MA的流场值,之后就是根据物面的边界条件(壁面速度的无穿透、无滑移以及绝热壁或等温壁等条件),确定虚拟点A和镜像点MA流场值之间的关系,从而得到虚拟点A处的流场信息。

图6 虚拟镜像对称方法Fig.6 Ghost mirror-symmetry method
镜像点流场信息的获得方法是通过邻近流场单元插值,对于虚拟点A的镜像点MA,其邻近的4个单元结点分别记作C、D、E、F,则MA点处的流场值为
(11)
式中:r1、r2、r3、r4分别为点MA到网格点C、D、E、F的距离。
3.2 曲率修正技术
在曲率修正对称方法(Curvature Corrected Symmetry Technique,CCST)[19]中,插值虚拟点的流场值是通过在物面附近虚构的涡流场得到的,涡流场的熵和总焓在法向上对称分布。Dadone和Grossman在针对贴体网格所发展的曲率修正对称方法的基础上,将其推广到非贴体的笛卡尔网格,即虚拟体单元方法(Ghost Body-Cell Method,GBCM)[20]。
如图7所示,虚拟点A和镜像点B的流场值满足:

图7 虚拟体单元方法Fig.7 Ghost body-cell method

(12)
值得一提的是,镜像点处的流场值是通过临近的流场单元插值得到的,若是4个临近单元中有2个或者2个以上在物体内部,可能会影响插值点处流场值的精度,因此要尽可能地使镜像点所有的插值点都在流场中。本文借鉴Forrer等提出的虚拟单元方法(Forrer’s Ghost Cell Method,FGCM)[21]对于镜像点的处理思路,针对该问题提出了新的镜像点位置取法,如图8所示,镜像点的位置不是取在和虚拟点A关于物面对称的位置A′,而是将线段AA′再延伸一个网格长度Δl,从而确保镜像点周围的插值点都在流场之中。Forrer和Berger等[21]的研究表明,这种位置取法可以提高计算的稳定性,而且不会降低边界处理的精度,其不足之处是局部的质量和动量守恒性难以保证。
Dadone等通过研究表明,在CCST方法基础上推广得到的GBCM在保证熵的增加和总焓的减少方面,相对于传统的物面边界处理方法有较大优势,有利于计算的稳定性和收敛性。

图8 镜像点位置调整Fig.8 Adjustment of position of mirroring point
3.3 多值点问题
使用浸入边界方法模拟研究具有尖点或薄体结构的外形时,会遇到多值点问题[20]。对于多值点问题的有效处理是自适应笛卡尔网格方法自动化处理任意复杂外形的关键技术之一,对于解算器的可靠度和精度有重要影响。
多值点单元的类型主要分为两种:流场中的多值点单元和物面内的多值点单元。在图9(a)中,网格点X作为目标单元Ω的计算模板点被调用,但是X与Ω在流场中异侧,不能够直接调用网格点X存储的流场值,X在此时即为流场多值点单元;在图9(b)中,上下两侧的目标单元Ω1、Ω2的计算模板点均用到虚拟单元G,该单元就存在两组流场值中,称之为物体内的多值点单元。
对于流场中的多值点单元,以图10中的网格点X为例,由于其与目标单元Ω异侧,不能直接使用其本身的流场值,而是将其看作上侧流场的虚拟单元,将网格点X关于上边界l1取对称点MX,通过虚拟镜像对称方法确定模版点X的流场值。
对于物体内的多值点单元,以图11中的单元G为例,上下两侧目标单元Ω1、Ω2的计算模板点均用到它,需要对G分别关于l1、l2取镜像点M1、M2,通过镜像虚拟对称方法确定其对应的两组流场值,并分别存储,根据目标单元的位置进行调用。

图9 多值点单元类型Fig.9 Types of multi-valued grids
对于多值点单元的信息的存储,需要在网格数据结构中多分配一块内存,以存储网格单元不同情况下的流场信息,根据具体情况选择要调用的数据,如图12和图13所示。这种方式虽然增加了存储量,但是相对于每次调用都重新计算的方式,计算量大大减少,调用方便高效。
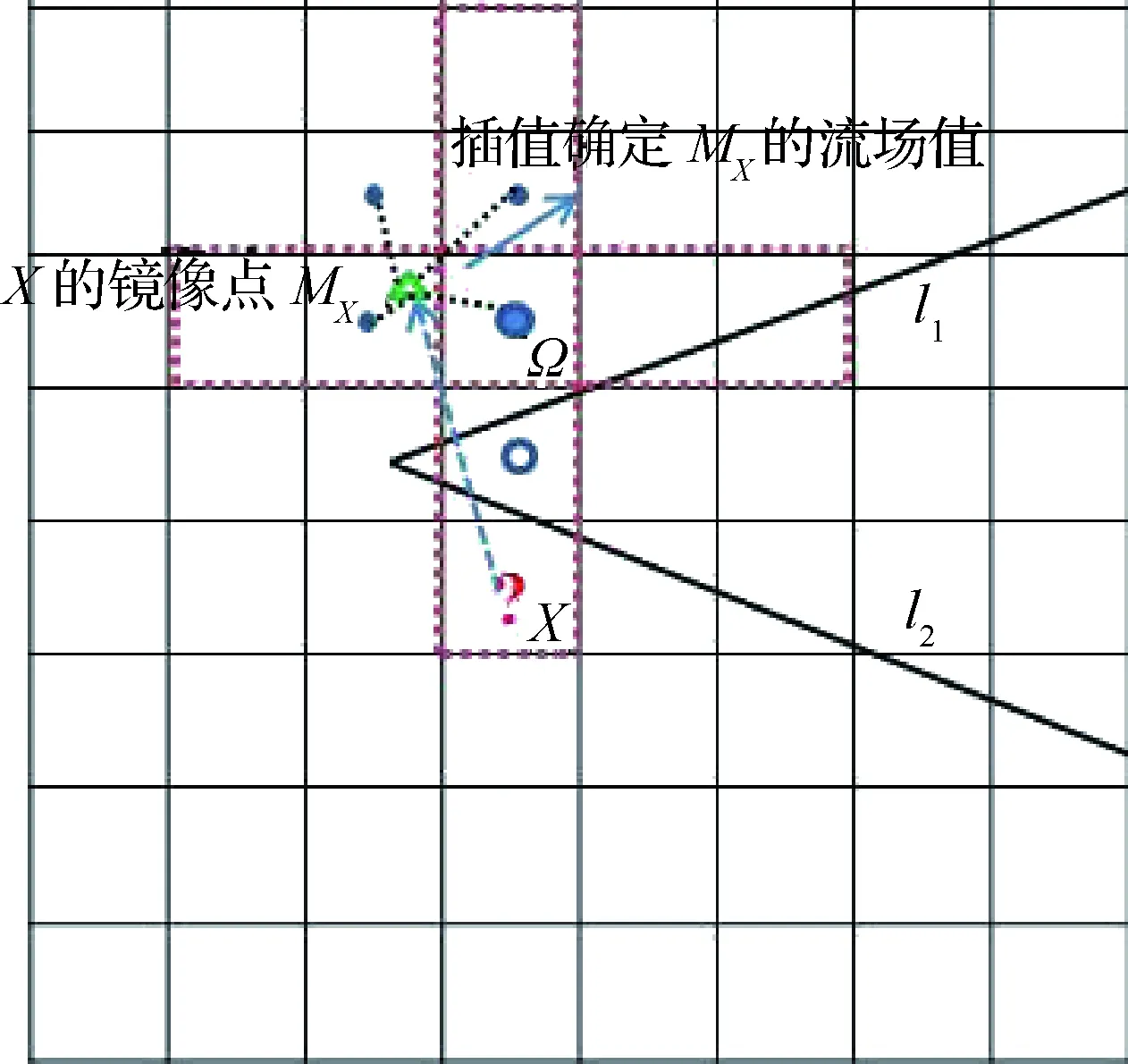
图10 流场多值点单元处理方法Fig.10 Processing method for multi-valued grid in flow field

图11 物体多值点单元处理方法Fig.11 Processing method for multi-valued grid inside the body

图12 流场多值点单元信息存储Fig.12 Information storage of multi-valued grids in flow field

图13 物体多值点单元信息存储Fig.13 Information storage of multi-valued grids inside the body
4 算例考核
下面针对圆柱绕流、前台阶流动和三角尖劈绕流以及压缩拐角流动等典型算例进行数值模拟,考核本文所发展的自适应笛卡尔网格生成技术和构建的黏性数值求解器的准确可靠性。
4.1 圆柱绕流
参照实验[22]进行参数设置,来流马赫数Ma=1.7,圆柱模型直径D=2.0 m,基于直径的雷诺数Re=2.0×105。初始计算网格边长为0.4 m,最大加密层数为8层,计算过程中基于速度的散度和旋度判据进行了4次自适应加密(Adaptive Mesh Refinement,AMR),即AMR=4,相应的自适应网格如图14(a)所示,图14(b)为马赫数云图,图15为密度(ρ)等值线和流场流线。
结合流场自适应网格和马赫数云图、密度等值线以及流线图可以看出,网格分布合理,层次清晰,曲线过渡光滑,外形信息保真度高,对激波间断、剪切层以及尾流涡等结构捕捉能力较强,网格自适应效果较好。
图16中,本文得到的表面压力系数Cp分布与实验及文献[23]结果吻合得较好。通过表1中分离点位置以及阻力系数等数据的对比,可以看出,本文所得到的结果与实验值更为接近,证明本文所发展的网格技术和构建的求解器对于超声速圆柱绕流问题的求解具有较高的精度和可靠性。

图14 流场自适应Cartesian网格和马赫数云图Fig.14 Adaptive Cartesian grid and Mach number contour of flow field

图15 密度等值线和圆柱尾流区流线Fig.15 Density contour lines and streamlines in wake region of cylinder

图16 表面压力系数分布对比Fig.16 Comparison of surface pressure coefficients distribution
表1本文数据与文献及实验结果对比
Table1Comparisonoftheproposeddataandreferenceandexperimentresults

参数文献[23]实验本文网格数目21600不存在32542分离点θ/(°)133.0112.0120.0阻力系数CD1.501.431.47
4.2 前台阶流动
前台阶激波反射流动问题包含激波的多次壁面反射,激波与激波相互作用,激波与中心膨胀波、接触间断的碰撞以及波系的相互干扰,是检验计算格式性能和网格方法的经典算例。
台阶的尺寸为3 m(长)×1 m(宽),台阶位于离风洞入口0.6 m处,高度为0.2 m。远场水平来流马赫数Ma=3.0,进、出口边界分别设为超声速入、出流边界,上、下壁面均设为滑移绝热固壁边界。相应的模型构建和初始网格生成如图17所示。其中初始单元长0.06 m,最大加密层数为5层。
计算在进行到t=4.0 s时得到的自适应网格和流场结果分别如图18和图19所示。结合两组图中的自适应网格和流场结果,自适应网格的分布清晰地捕捉了经壁面反射形成的λ型激波和马赫杆(Mach Stem)、三叉点处的滑移线、台阶前缘奇点处的中心膨胀波以及与壁面相撞形成的反射激波等结构,网格分布均匀有序,激波线过渡光滑,自适应效果较好。

图17 前台阶及初始计算网格Fig.17 Front step and initial computation grid

图18 t=4.0 s自适应网格Fig.18 Adaptive grid at t=4.0 s

图19 t=4.0 s流场计算结果Fig.19 Calculated results of flow field at t=4.0 s
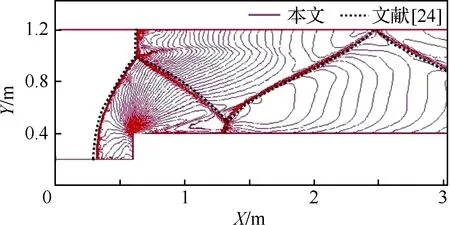
图20 激波线位置与文献[24]结果对比Fig.20 Comparison of the shock wave line in this paper and Ref.[24]
在图20中,流场等值线分布与文献[24]结果符合较好。该文献基于非结构网格,采用的是时空三阶精度有限元格式(Third-order Taylor Galerkin Convection,TTGC),本文与其h=0.01(网格数为56 892)的结果相对比,在前缘弓形激波靠近水平壁面处,本文的激波线与壁面垂直性更好,更贴近理论情况,并且对于前缘弓形激波和马赫杆的捕捉更加精细;在网格数目方面,本文网格数目为26 238,说明在流场波系较复杂时,本文发展的网格方法网格数目较少。综上,本文所发展的网格生成技术和构建的数值求解器在计算前台阶流动问题的可靠性和优势方面得到验证。
4.3 尖劈绕流
为了考察本文所发展的方法技术对于多值点问题的处理能力,选取三角尖劈模型,在超声速来流情况下进行流场的模拟研究。
尖劈模型顶角θ=30°,高度H=1.0 m,来流马赫数Ma=2.2,基于尖劈高度的雷诺数Re=1.0×105。初始计算网格长0.2 m,最大加密次数为7,AMR=5,相应的流场自适应网格和流场结果如图21所示。

图21 流场自适应网格及流场结果Fig.21 Adaptive grid and results of flow field
根据流场解的速度散度和旋度判据生成的自适应网格,对于附体斜激波、膨胀波、剪切层以及分离区等流场结构和特征捕捉清晰,网格分布均匀,层次分明,冗余网格和网格空洞很少,进一步证明了本文网格生成方法具有很好的自适应能力和较高的质量,并且能够有效处理多值点问题。
下面将不同马赫数下的附体斜激波的激波角与理论值进行对比,其理论公式[25]为
式中:η为斜面偏转角;β为斜激波角,即附体斜激波的激波线与水平方向的夹角。
在表2中,对于附体斜激波的激波角,本文得到的计算值和理论值相差较小,均在4%以下,证明了本文方法能够较准确地捕捉激波位置,具有较高的精度和可靠性。
表2斜激波角计算值与理论值对比
Table2Comparisonofcalculatedvalueandtheoreticalvalueofobliqueshockwaveangles
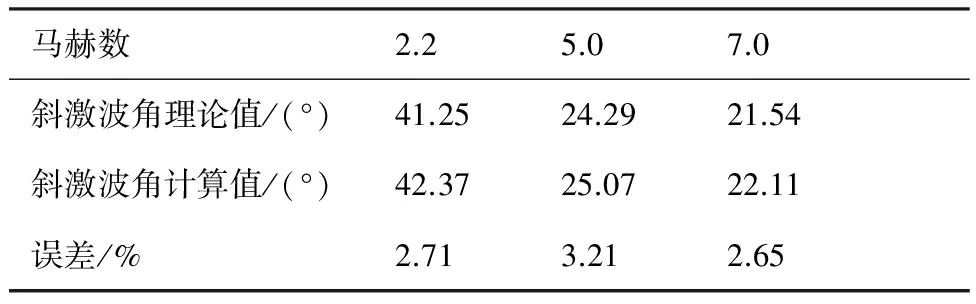
马赫数2.25.07.0斜激波角理论值/(°)41.2524.2921.54斜激波角计算值/(°)42.3725.0722.11误差/%2.713.212.65
4.4 压缩拐角流动
压缩拐角流动问题的几何边界虽然简单,但包含了剪切层、流动分离和再附等多种复杂流动结构和现象。本文针对该问题进一步考核本文的网格技术和构建的数值求解器对于复杂流动问题求解的准确可靠性。
选取Ma=3.0,基于压缩拐角模型的雷诺数Re=7.5×104,压缩角度为24°,总温T0=300 K,壁面温度Tw=297 K。网格最大加密层数为9层,AMR=5。相应的自适应网格和流场结果如图22所示。
从图22可以看出,本文所发展的自适应笛卡尔网格技术对于压缩拐角的波系结构可以清晰的捕捉,自适应效果较好。由压缩坡面引起的逆压梯度影响了层流边界层,对于流动产生了阻碍,导致入口边界附近产生了一道诱导激波。在拐点附近的上游区域,流动产生分离,形成了分离激波和分离区,之后在压缩坡面上的某一位置发生再附现象,边界层重新发展,并形成再附激波。分离激波和再附激波相互作用,沿压缩坡面向上传播。
改变模型压缩面角度,在压缩角分别为15°、18°和24°的情况下进行数值模拟,并将计算得到的表面压力系数Cp分别与实验值进行对比,如图23所示。
通过不同压缩角情况下表面压力系数的计算结果和实验结果的对比发现,本文计算结果和实验符合较好,进一步证明了本文方法技术和求解器对于压缩拐角流动问题求解的可行性和可靠性。另外,在压缩角为24°时,两者相差相对较大,Rudy等[26]在数值模拟过程中也遇到过类似问题,认为是由于实验中存在三维效应,对于实验的测量值有所影响。

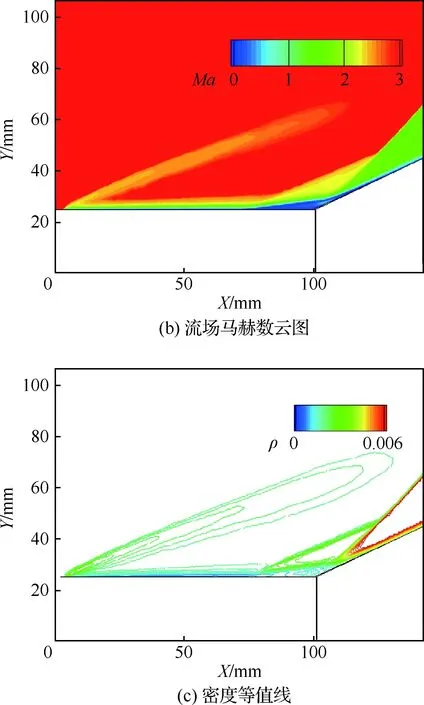
图22 流场自适应网格及流场结果Fig.22 Adaptive grid and results of flow field
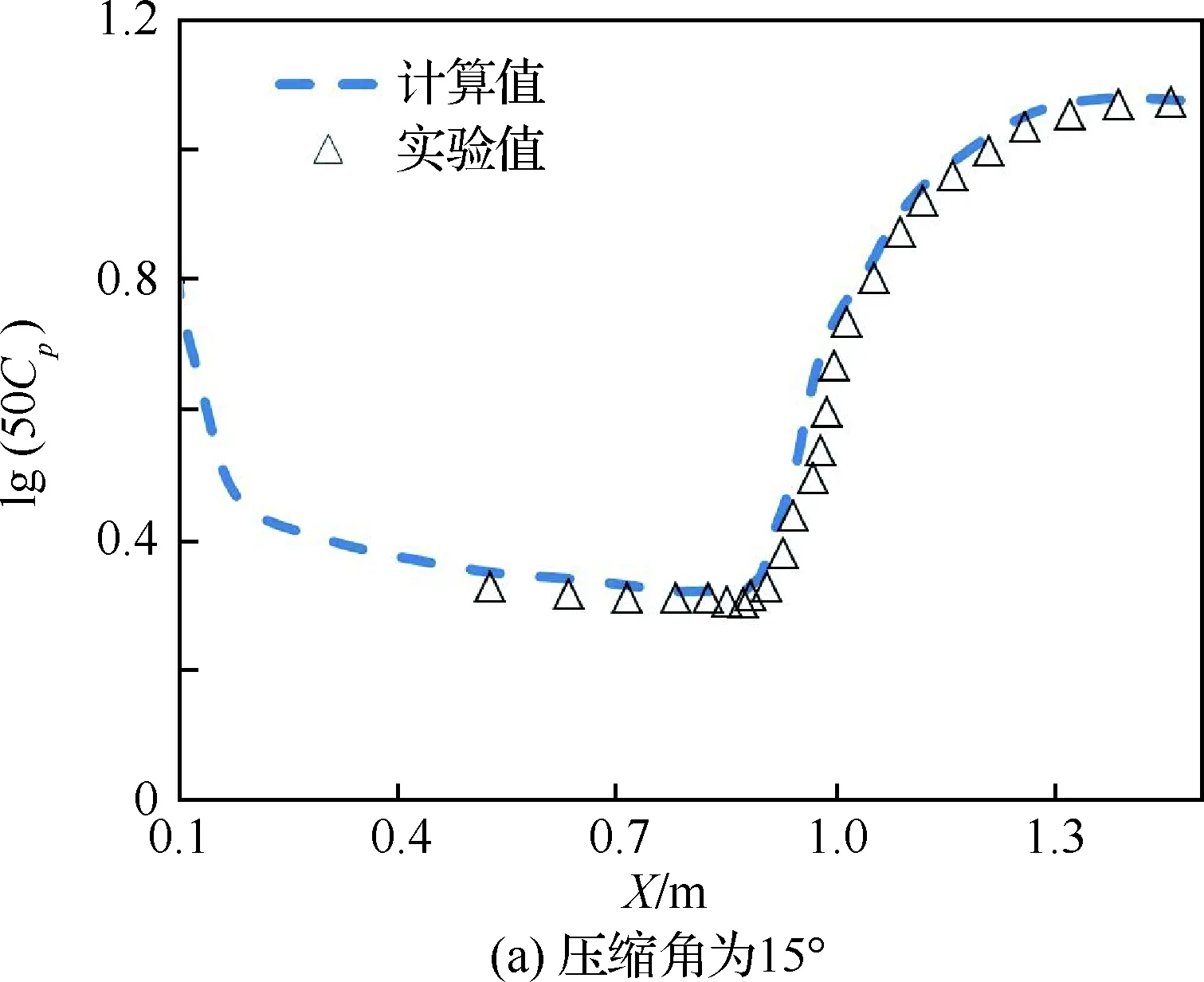
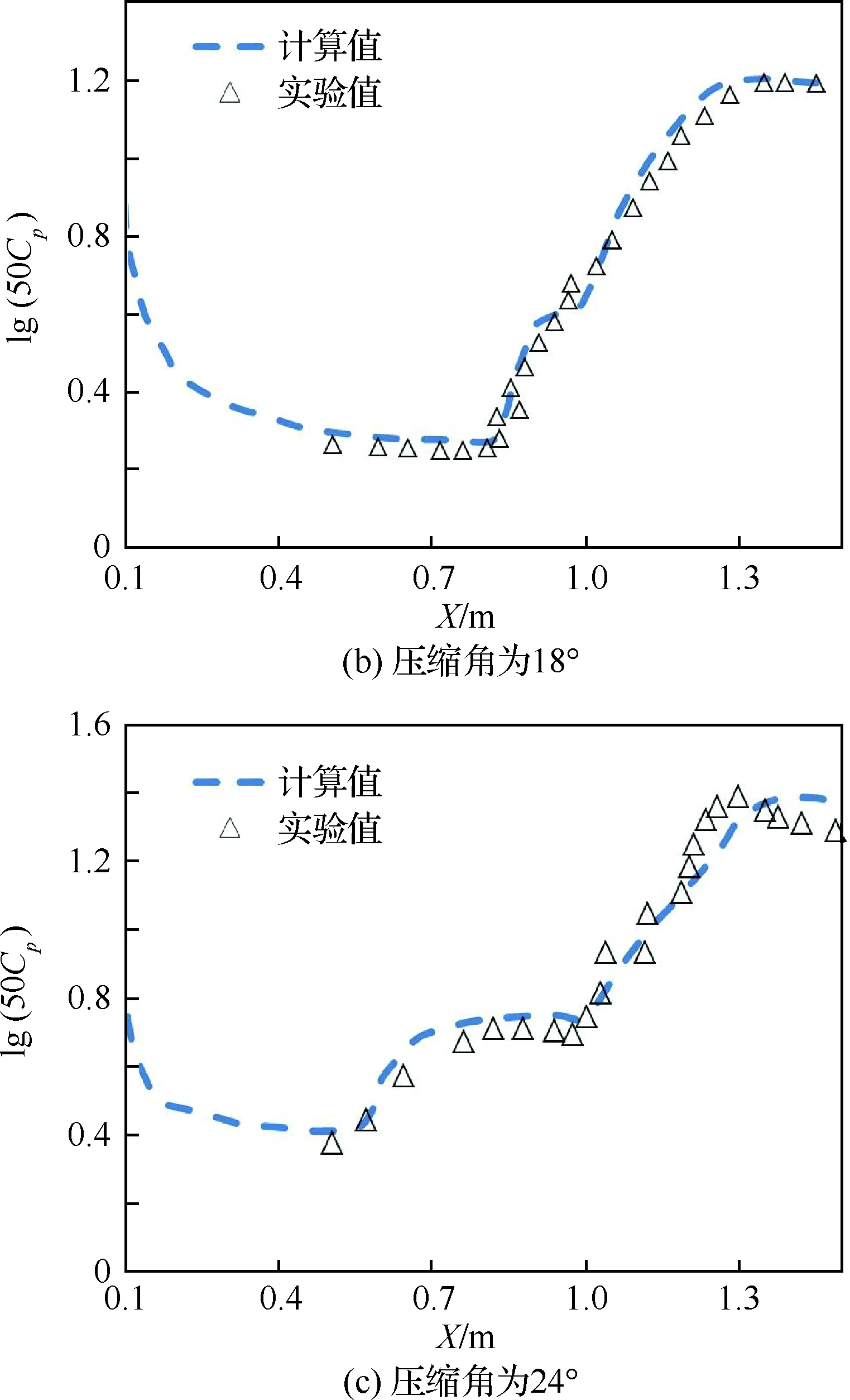
图23 不同压缩角下计算与实验表面压力系数对比Fig.23 Comparison of surface pressure coefficients at different compression corners in calculation and experiment
5 结 论
本文针对二维情况下含强间断的超声速黏性流动问题,发展了自适应笛卡尔网格生成技术和黏性物面边界的处理方法,并构建了相应的Navier-Stokes方程数值求解器,在此基础上进行了典型算例的考核验证。
1) 在笛卡尔网格自适应技术方面,本文选用叉树数据结构进行网格信息的存储,分别从物体外形和流场特征出发进行网格的自适应加密和粗化,发展了一种自动高效的自适应笛卡尔网格生成方法,具有流场特征捕捉效果好、自动化程度高等特点。
2) 对于黏性物面边界的处理,本文基于浸入边界方法,结合虚拟镜像对称方法和曲率修正技术进行黏性物面边界的处理,同时建立了多值点问题的处理技术,发展了一种在笛卡尔网格下可有效模拟黏性物面边界条件的方法,经算例考核,证明该方法具有较高的精度和可靠性。
3) 在数值求解器方面,针对Navier-Stokes方程,建立了具有二阶精度和保持TVD性质的全离散格式,避免了解在激波间断附近的非物理振荡;构建了粗细网格间悬挂网格的插值方法,可以有效应用于离散方程的求解。
目前,基于自适应笛卡尔网格的超声速黏性流动数值模拟尚未工程实用化,有进一步发展的需求。后续工作的首要目标是将本文方法推广到三维任意复杂外形的流动问题模拟中,重点研究三维复杂几何外形物体的自动化处理方法,建立相应的自适应笛卡尔网格生成技术,并针对Navier-Stokes方程构建黏性数值求解器。同时,通过自适应笛卡尔网格生成技术与人工智能技术的结合,发展智能化、自动化生成高质量网格的方法;发展各向异性的笛卡尔网格生成技术,减少网格数量和数据存储量;将生成笛卡尔网格的软件直接与模型生成和处理软件对接,尽可能地形成一体化、软件化和商品化。
参 考 文 献
[1] MAVRIPLIS D J. An advancing front Delaunay triangulation algorithm designed for robustness[J]. Journal of Computational Physics, 1995, 117(1): 90-101.
[2] ITO Y, NAKAHASHI K. Unstructured hybrid grid generation baseds on isotropic tetrahedral grids: AIAA-2002-0861[R]. Reston, VA: AIAA, 2002.
[3] KALLINDERIS Y, WARD S. Prismatic grid generation with an efficient algebraic method for aircraft configuration: AIAA-1992-2721[R]. Reston, VA: AIAA, 1992.
[4] DE ZEEUW D L. A quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D]. Michigan: University of Michigan, 1993.
[5] MURAT B. Quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D]. Michigan: University of Michigan, 2005.
[6] ROBERT R A, VLADIMIR I K. Direct simulation Monte Carlo with octree Cartesian mesh[J]. AIAA Journal, 2012, 20(2): 25-28.
[7] FUJIMOTO K, FUJII K, WANG Z J. Improvements in the reliability and efficiency of body-fitted Cartesian grid method: AIAA-2009-1173[R]. Reston, VA: AIAA, 2009.
[8] UDAYKUMAR H S. Multiphase dynamics in arbitrary geometries on fixed Cartesian grids[J]. Journal of Computational Physics, 1997, 137(2): 366-405.
[9] UDAYKUMAR H S. A sharp interface Cartesian grid method for simulating flow with complex moving boundaries[J]. Journal of Computational Physics, 2001, 174(1): 345-380.
[10] MARSHALL D D. Extending the functionalities of Cartesian grid solvers: Viscous effects modeling and MPI parallelization[D]. Georgia: Georgia Institute of Technology, 2002.
[11] FORRER H, JELTSCH R. A higher order boundary treatment for Cartesian-grid method[J]. Journal of Computational Physics, 1998, 140(2): 259-277.
[12] JAE-DOO L, RUFFIN S M. Development of a turbulent wall-function based viscous Cartesian-grid methodology: AIAA-2007-1326[R]. Reston, VA: AIAA, 2007.
[13] JAE-DOO L. Development of an efficient viscous approach in a Cartesian grid framework and application to rotor-fuselage interaction[D]. Georgia: Georgia Institute of Technology, 2006.
[14] DE ZEEUW D L. A wave-model-based refinement criterion for adaptive-grid computation of compressible flow: AIAA-1992-0332[R]. Reston, VA: AIAA, 1992.
[15] 张涵信. 无波动、无自由参数的耗散差分格式[J]. 空气动力学学报, 1988, 6(2): 143-165.
ZHANG H X. A non-oscillatory, containing no free parameters and dissipative scheme[J]. Acta Aerodynamica Sinica, 1988, 6(2): 143-165 (in Chinese).
[16] VAN LEER B. Flux vector splitting for Euler equations[J]. Lecture Notes in Physics, 1982: 507-512.
[17] ENGQUIST B, MAJDA A. Absorbing boundary conditions for the numerical simulation of waves[J]. Mathematics of Computation, 1977, 31: 629-651.
[18] GUSIAFSSON B, SANDSTROM A. Incompletely parabolic problems in fluid dynamics[J]. SIAM Journal on Applied Mathematics, 1978, 35: 343-357.
[19] DADONE A, GROSSMAN B. An immersed body methodology for inviscid flows on Cartesian grids: AIAA-2002-1059[R]. Reston, VA: AIAA, 2002.
[20] DADONE A, GROSSMAN B. Surface boundary conditions for the numerical solution of the Euler equations[J]. AIAA Journal, 1994, 32(2): 285-293.
[21] FORRER H, BERGER M. Flow simulations on Cartesian grids involving complex moving geometries[C]∥Proceedings of 6th International Conference on Hyperbolic Problems, 1998.
[22] BASHKIN V A, VAGANOV A V, EGOROV I V, et al. Comparison of calculated and experimental data on supersonic flow past a circular cylinder[J]. Fluid Dynamics, 2002, 37(3): 473-483.
[23] MUNIKRISHNA N, LIOU M S. A Cartesian based body-fitted adaptive grid method for compressible viscous flows[R]. Reston, VA: AIAA, 2009.
[24] 鲁阳, 邹建锋, 郑耀. 基于非结构网格的TTGC有限元格式的实现及在超声速流动中的应用[J]. 计算力学学报, 2013, 30(5): 712-722.
LU Y, ZOU J F, ZHENG Y. Unstructured grids based on TTGC finite element scheme and its application to supersonic flows[J]. Chinese Journal of Computational Mechanics, 2013, 30(5): 712-722 (in Chinese).
[25] BOIRON O, CHIAVASSA G, DONAT R. A high-resolution penalization method for large Mach number flows in the presence of obstacles[J]. Computers & Fluids, 2009, 38(3): 703-714.
[26] RUDY D H, THOMAS J L, KUMAR A. Computation of laminar viscous-inviscid interactions in high-speed internal flows[J]. AIAA Journal, 1991, 29(7): 1108-1113.

