追逃定性微分对策中界栅的确定
于 飞, 李 擎, 张 昊
(北京信息科技大学高动态导航技术北京市重点实验室,北京 100101)
0 引言
无人机与无人车是信息化装备体系的重要组成部分,在军事中投入使用可显著提高军事作战能力,此外,可以在核、生物和化学战争环境中执行物资运输、目标识别以及环境勘测等任务。微分对策理论为军事对抗问题提供了较为完善的模型[1-4],定性微分对策中界栅的确定是研究热点之一[5-8]。应用追逃微分对策分析时,对局环境中的障碍物的影响会被考虑[9-10]。文献[11]为了解决固定翼无人机追踪地面移动车辆的问题,运用微分对策理论进行定量分析,得到防止目标丢失的最优策略。本文在无人机、无人车的追捕对抗过程中,考虑对局环境中障碍物的影响,定性分析追逃微分对策,确定其分界界栅。无人机配有固定摄像头装置,可以提供足够的视觉分辨率,在野外作战现场自动跟踪地面的无人车,使其始终处于观测范围之内;无人车则根据自身运动特性以及周围环境来躲避无人机的追踪。对局双方为单一的追捕者和躲避者,无人机希望最大化延长无人车在其有效可视范围之内的时间,无人车希望尽快逃避追捕。
1 建模与分析
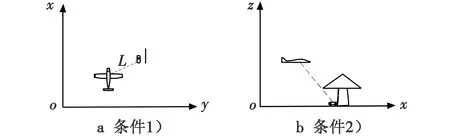
设定P代表追捕方无人机,E代表躲避方无人车。假设P和E分别以速度vp,ve在平面上匀速运动。P的目的是迫使局中人E进入目标集D,并捕捉E,从而结束对策,而E的目标正好相反,试图阻止或者拖延对策结束,如图1所示。
P可以以速度vp在平面内任意活动,滚转角、俯仰角保持不变,偏航角控制为v;躲避E以速度ve运动,转向控制记为u;P和E均可以完成瞬时的转向。博弈具有一个完美的状态反馈信息结构,因此,当参与者在进行博弈时,能够不受干扰地知晓整个过程中的状态变化,从而确定下一个动作。
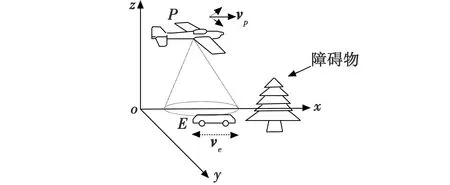
图1 对局示意图Fig.1 Game diagram
对局环境中存在树木形成的障碍,这会对双方产生影响。追捕者希望在尽可能长的时间内将躲避者保持在可视区域,躲避者希望在最短的时间内打破视线。某一时刻,如果躲避者不在捕获者的视线之内,此时对局终止。
(1)
由于无人车可以瞬时转向,因此其方向控制:当u=+1时,向右运动;当u=-1时,则向左运动。
在设定的场景中,对局双方视为点运动物体,除了有界速度之外,它们的运动没有任何限制。与经典情况一致,这里无人机与无人车的速度之比k=vp/ve>1。对局环境中仅包含限制追捕者和躲避者运动的障碍,对局双方都有独立决策权,他们根据实际情况采取决策,控制局势朝着有利于自己的方向发展。
P和E都可以控制各自的方向,且各自转向控制分别为v,u。当P与E之间的距离小于L时,则认为被捕获,此时对局结束。作简单的分析不难得到表1中的4种结局。
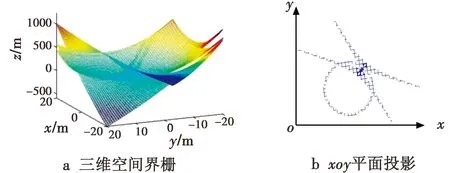
情况2中P在机动性能上占绝对优势,所以总能捕获到E;情况3中E在机动性能上占绝对优势,所以总能逃脱P的追捕。这两种情况对局结果是确定的,没有深入研究的意义,下面将对情况1和情况4这种双方互有优、劣势的对局结果进行探讨。情况4中vp>ve,v 表1 运动性能与结局的关系 定义d=(xe-xp,ye-yp,ze-zp)为追捕者的瞬时位置到躲避者的瞬时位置的指向向量,ve(t)和vp(t)分别为t时刻躲避者与追捕者的速度向量,于是有‖ve(t)‖=ve<‖vp(t)‖=vp。 定理1在任一时刻t0,如果追捕者的速度向量vp(t0)与相对位置向量d(t0)的内积非正,即如果 d(t0),vp(t0)≤0 (2) 则t≥t0时P不能捕获到E,E成功逃脱。 证明 不失一般性,设t0=0。为了证明这个定理,只需找到一个E成功逃脱的例子。假设在t≥0的任意时刻,P都不改变其速度方向,相对位置向量d满足 (3) (4) 鉴于P的约束性,定理1的证明说明,只有P的速度向量的分量指向E时捕获才会发生,这种情况下P的最优策略是尽快增大指向E的速度分量,如果这个分量增加得较慢,捕获将可能无法完成。另一方面,如果P一直没有指向E的速度分量,则E可凭借其机动性优势成功逃避追捕。 如表1所示,在情况1和情况4下,P和E各有优势,对策空间可以划分为 2 部分。一部分为捕获区,另一部分为躲避区,其分界面为界栅,记作D。 H(x,y,u,v,λ)=λ1vpcosv+λ2vpsinv+λ3veu (5) Hp(v)=vp(λ1cosv+λ2sinv) (6) He(v)=λ3veu (7) 在λ1,λ2均为0的情况下,v可以取任何值,P可以遵循任何控制策略。 类似地,如果λ3=0,那么u可以取任何值,并且E可以遵循任何控制策略。这些条件代表了哈密尔顿算子的奇异点。 H(x,y,u,v,λ)表示状态的变化率。如果轨迹X在∂D上或者充分接近∂D,并且H(x,y,u,v,λ)>0,那么轨迹X不能穿过∂D;反之,即H(x,y,u,v,λ)<0则轨迹X穿过∂D,此时对局结束。因此,从P与E各自的目的出发,P欲使H<0,而E欲使H>0。哈密尔顿函数H(x,y,u,v,λ)中含有控制变量u,v,因此P应该选择最优策略v,使H(x,y,u,v,λ)∂D在目标边界集合∂D上取得尽可能小的负值以保证对局结束,而E应选择最优策略u使H(x,y,u,v,λ)∂D取得尽可能大正值以实现逃脱,即 (8) (9) (10) 式中:u=+1,说明沿x轴的正方向运动;u=-1,意味着朝相反方向运动。所以可得 (11) 树木覆盖会对无人机和无人车的视线造成影响,进而影响对局结果。本文把树木作为对局环境中的障碍,对树木的影响进行建模分析。追捕者成功追捕到目标,或者目标丢失都会导致对局结束。 按照设定场景,给出了树木障碍物存在的情况下对局终止的两个充分条件:1) 当无人车处于无人机的有效观测距离之外时,认为目标丢失;2) 虽然无人车在无人机的有效观测距离之内,但是两者视线被障碍物阻挡,相互不可见。以上两种情况分别对应图2a和图2b。 图2 对局情况分析Fig.2 Game situation analysis (xe-xp)2+(ye-yp)2-L2≤0 (12) 同样,选取三角形底边顶点为(xT,yT),将条件2)向xoz面投影,条件2)可以表示为 (13) 上述两个条件得到满足时,对局终止,可得终端集 F=(xe-xp)2+(ye-yp)2-L2+(xp-xT)· (14) 由终端集可得参数方程 (15) 式中,s=(s1s2s3)T。 在界栅D上的法线向量λ满足 (16) 因为法线向量的长度是任意的,故可取λ为单位法线向量,在∂D上同样有λT·λ∂D=1,联立式(10)可以求出确定目标边界集∂D上的单位法线向量λ。 (17) 代入式(9),可以得到最优策略u*,v*。 (18) 积分可得 (19) 设置P的初始化坐标为(0 m,0 m,29 m),E的初始坐标为(3 m,5 m,0 m),速度比为k=1.14,捕获半径L=200 m。当障碍点在(5 m,5 m,5 m)时,得到图3a所示三维空间界栅。 图3 界栅Fig.3 The barrier 界栅D对应的是穿过BUP的半透曲面,为方便观察将图3a朝xoy平面投影得到图3b。图3b中圆和双曲圆弧代表目标集在xoy平面的投影,蓝色阴影部分是由界栅D和目标集围成的捕获区,在捕获区内运动,轨迹将到达目标集的边界并穿过。在此区域内,只要P使得E进入该区,则无论E采取何种策略,在P选择适当的策略下,E再也不能逃出该区,即捕获E。捕获区之外为躲避区,在此区域上,只要E初始位置在该区中,不管P采用何种策略,E总能采取适当的策略躲避P的捕获。 分析对局环境中存在障碍物约束的追逃定性微分对策,建立了无人机、无人车的运动模型,通过分析确定了躲避区与捕获区的分界界栅。不同的障碍物对界栅的形状会有不同的影响,分析界栅的形状、对策空间的划分对于作战能力评价、指导指挥训练、作战等都有一定的意义。未来,对局双方更复杂的运动模型,以及其他形状的障碍物将会进一步讨论。 参 考 文 献 [1] 原鑫,李擎,苏中.基于微分对策理论的两车碰撞问题[J].北京信息科技大学学报:自然科学版,2016,31(5):68-72. [2] 龚华军,杨长锋,王彪,等.无人机的追逃对抗仿真研究[J].控制理论与应用,2009,26(9):1019-1022. [3] 车竞,郑凤麒.基于微分对策的追逃对抗仿真[J].飞行力学,2014,32(4):372-375. [4] 车竞,钱炜祺,和争春.基于矩阵博弈的两机攻防对抗空战仿真[J].飞行力学,2015,33(2):173-177. [5] 佟明安,王立新.三维空间双机格斗的捕捉区和危险区[J].航空学报,1989,10(11):536-544. [6] 张秋华,孙毅,黄明明,等.近地共面轨道上两飞行器在径向连续小推力下的追逃界栅[J].控制与决策,2007,22(5):530-534. [7] 黄银春.导弹拦截飞机末端制导制导律和界栅的研究[D].哈尔滨:哈尔滨工业大学,2014. [8] 王发坤,秦艳琳.三维空间中追逃对抗定性微分对策模型研究[J].舰船电子工程,2008,28(7):14-16,181. [9] BHATTACHARYA S,HUTCHINSON S,BASAR T.Game-theoretic analysis of a visibility based pursuit-evasion game in the presence of obstacles[C]//American Control Conference,2009:373-378. [10] OYLER D W,KABAMBA P T,GIRARD A R.Pursuit-evasion games in the presence of obstacles[J].Automatica,2016,65(C):1-11. [11] QUINTERO S A P,HESPANHA J P.Vision-based target tracking with a small UAV:optimization-based control strategies[J].Control Engineering Practice,2014(32):28-42.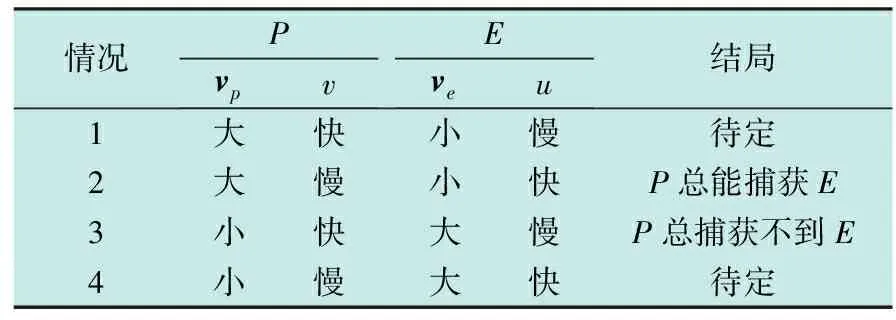
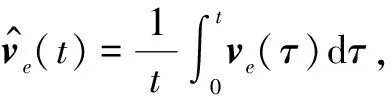
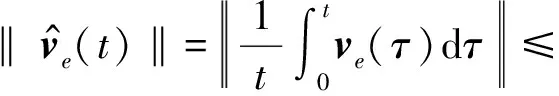
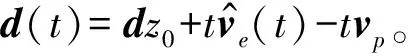
2 对局策略
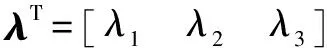
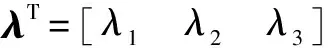
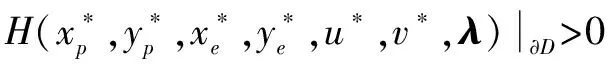
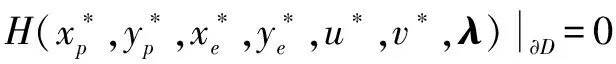
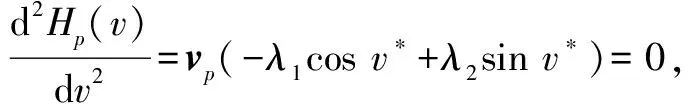
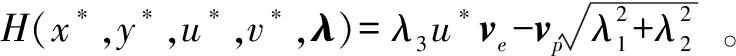
3 界栅的确定
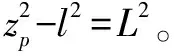
(ye-yT)-(yp-yT)(xe-xT)=0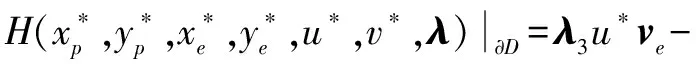
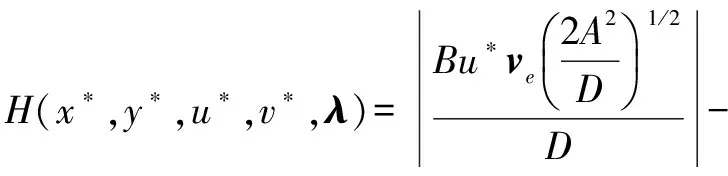
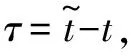
4 总结与展望

